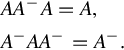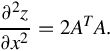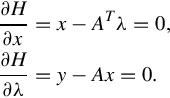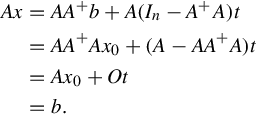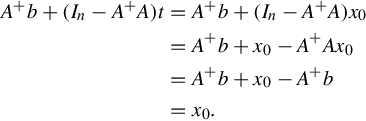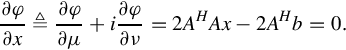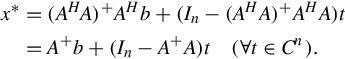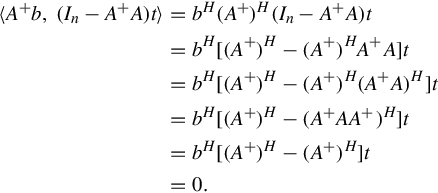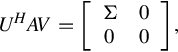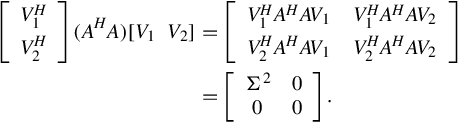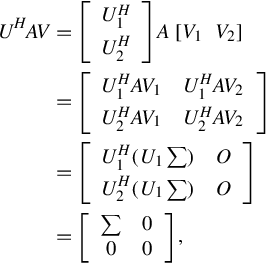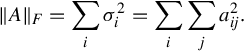3.1.1 The left inverse and right inverse

The usual matrix inverse is defined as a two-side inverse, i.e., AA⁻¹ = I = A⁻¹A because we can multiply the inverse matrix from the left or from the right of matrix A and we still get the identity matrix. This property is only true for a square matrix A.

For a rectangular matrix A, we may have a generalized left inverse or left inverse for short when we multiply the inverse from the left to get identity matrix A_left⁻¹A = I. Similarly, we may have a generalized right inverse, or right inverse for short, when we multiply the inverse from the right to get the identity matrix AA_right = I.

In general, the left inverse is not equal to the right inverse. The generalized inverse of a rectangular matrix is related to the solving of system linear equations Ax = b. The solution to a normal equation is x = (A^TA)⁻¹A^Tb, which is equal to x = A⁻b. The term

$\begin{array}{l}\hfill A^{-}=A_{\mathrm{left}}^{-1}={(A^{T}A)}^{-1}{A}^T\end{array}$

is often called as generalized left inverse. Yet another pseudo-inverse can also be obtained by multiplying the transpose matrix from the right and this is called a generalized right inverse

$\begin{array}{l}\hfill A^{-}=A_{\mathrm{right}}^{-1}=A^T{(A{A}^T)}^{-1}.\end{array}$

3.1.2 Moore-Penrose inverse

It is possible to obtain a unique generalized matrix. To distinguish the unique generalized inverse from other nonunique generalized inverses A⁻, we use the symbol A⁺. The unique generalized inverse is called the Moore-Penrose inverse. It is defined using the following four conditions:

(1) AA⁺A = A,

(2) A⁺AA⁺ = A⁺,

(3) (AA⁺)^T = AA⁺,

(4) (A⁺A)^T = A⁺A.

The first condition AA⁺A = A is the definition of a generalized inverse. Together with the first condition, the second condition indicates the generalized inverse is reflexive (A⁻)⁻ = A. Together with the first condition, the third condition indicates that the generalized inverse is the least square solution that will minimize the norm of error ${min}_x\parallel b-Ax\parallel .$ The fourth condition above demonstrates the unique generalized inverse.

Properties of generalized inverse of matrix: Some important properties of generalized inverse of matrix are:

1. The transpose of the left inverse of A is the right inverse A_right⁻¹ = (A_left⁻¹)^T. Similarly, the transpose of the right inverse of A is the left inverse A_left⁻¹ = (A_right⁻¹)^T.

2. A matrix A_m×n has a left inverse A_left⁻¹ if and only if its rank equals its number of columns and the number of rows is more than the number of columns ρ(A) = n < m. In this case A⁺A = A_left⁻¹A = I.

3. A matrix A_m×n has a right inverse A_right⁻¹ if and only if its rank equals its number of rows and the number of rows is less than the number of columns ρ(A) = m < n. In this case A⁺A = AA_right⁻¹ = I.

4. The Moore-Penrose inverse is equal to left inverse A⁺ = A_left⁻¹, when ρ(A) = n < m and equals the right inverse A⁺ = A_right⁻¹, when ρ(A) = m < n. The Moore-Penrose inverse is equal to the matrix inverse A⁺ = A⁻¹, when ρ(A) = m = n.

3.1.3 The minimization approach to solve an algebraic matrix equation

The generalized inverse of the matrix has been used extensively in the areas of modern control, least square estimation and aircraft structural analysis. It is the purpose of this note to extend the results by presenting a unified framework that provides geometric insight and highlights certain optimal features imbedded in the generalized inverse.

Consider the algebraic matrix equation

$\begin{array}{l}\hfill y=Ax,\end{array}$

where A is an n × m constant matrix, y is a given n vector, and x is an m vector to be determined. For the trivial case where n = m and A is a nonsingular matrix, i.e., rank(A) = n, a unique solution to Eq. (3.1) exists and is given by

$\begin{array}{l}\hfill x=A^{-1}y,\end{array}$

where A⁻¹ denotes the inverse of A.

For the case n≠m, the expression of x in terms of y involves the generalized inverse of A, denoted A⁺, and thus

$\begin{array}{l}\hfill x=A^{+}y.\end{array}$

In the following cases it will be shown that A⁺, for either n > m or n < m, may be viewed as a solution to a certain minimization problem.

(1) Case A: n > m

With no loss of generality it can be assumed that A is of full rank, i.e.,

$\begin{array}{l}\hfill \mathrm{rank}(A)=m\end{array}$

however, rank (A) < n. It is possible to delete the dependent columns of A, set the respective unknown components of x equal to zero, and reduce the problem to the case in which Eq. (3.4) is satisfied. Since the m columns of A do not span the n dimensional space R_n, an exact solution to Eq. (3.1) cannot be obtained if y is not contained in the subspace spanned by the columns of A. Thus, one is motivated to seek approximate solutions, the best of which is the one that minimizes the Euclidian norm of the error. Let the error e be given by

$\begin{array}{l}\hfill e=y-Ax.\end{array}$

Then let z be given by

$\begin{array}{l}\hfill z=\parallel e{\parallel }^2=e^{T}e={(y-Ax)}^T(y-Ax),\end{array}$

where the superscript “T” denotes the transpose. Evaluation of the gradient of z with respect to x yields

$\begin{array}{l}\hfill \frac{\partial z}{\partial x}=-2A^{T}y+2A^{T}Ax=0.\end{array}$

The Hessian matrix is

$\begin{array}{l}\hfill \frac{{\partial }^{2}z}{\partial x^2}=2A^{T}A.\end{array}$

From Eq. (3.7), x is given by

$\begin{array}{l}\hfill x={(A^{T}A)}^{-1}{A}^{T}y.\end{array}$

By virtue of A having full rank, (A^TA) is a positive definite matrix. Thus (A^TA)⁻¹ exists and the Hessian matrix is positive definite, implying that a minimum was obtained. In this case (n > m) the generalized inverse of A is given by

$\begin{array}{l}\hfill A^{+}={(A^{T}A)}^{-1}{A}^T.\end{array}$

It is interesting to note that if y is contained in the subspace spanned by the columns of A, Eq. (3.9) yields an exact solution to Eq. (3.1), i.e., ∥e∥ = 0. The optimal feature of Eq. (3.9) has found extensive applications in data processing for least square approximations. In closing it should be noted that Eq. (3.9) can be obtained by invoking the Orthogonal Projection Lemma, thus providing a geometric interpretation to the optimal feature of Eq. (3.10).

(2) Case B: n < m

Again, without loss of generality, it can be assumed that A is of full rank, i.e.,

$\begin{array}{l}\hfill \mathrm{rank}(A)=n.\end{array}$

If, however, rank(A) < n, it implies that some of the equations are merely a linear combination of the others and therefore may be deleted without loss of information, thereby reducing the case rank(A) < n to the case rank(A) = n. Moreover, if A is a square singular matrix, it can be reduced to case B after proper deletion of the dependent rows of A.

Eqs. (3.1), (3.11) with n < m yield an infinite number of solutions, the “optimal” of which is the one having the smallest norm. Therefore one is confronted with a constrained minimization problem, where the minimization of ∥x∥ (or equivalently $\frac{\parallel x{\parallel }^2}{2}$) is to be accomplished subject to Eq. (3.1). Adjoining the constraint, via a vector of Lagrange multipliers (λ), the objective function to be minimized is

$\begin{array}{l}\hfill H=\frac{1}{2}\parallel x{\parallel }^2+{\lambda }^T(y-Ax)=\frac{1}{2}{x}^{T}x+{\lambda }^T(y-Ax).\end{array}$

By evaluating the respective gradients

$\begin{array}{ll}\hfill \frac{\partial H}{\partial x}& =x-A^T\lambda =0,\hfill \end{array}$

$\begin{array}{ll}\hfill \frac{\partial H}{\partial \lambda }& =y-Ax=0.\hfill \end{array}$

From Eq. (3.13), one has

$\begin{array}{l}\hfill x=A^T\lambda .\end{array}$

Substitution of Eq. (3.15) into Eq. (3.14) yields

$\begin{array}{l}\hfill y=A{A}^T\lambda .\end{array}$

That is

$\begin{array}{l}\hfill \lambda ={(A{A}^T)}^{-1}y.\end{array}$

The existence of (AA^T)⁻¹ is guaranteed by virtue of Eq. (3.11). Substitution of Eq. (3.17) into Eq. (3.15) yields

$\begin{array}{l}\hfill x=A^T{(A{A}^T)}^{-1}y.\end{array}$

In this case (n < m) the generalized inverse of A is given by

$\begin{array}{l}\hfill A^{+}=A^T{(A{A}^T)}^{-1}.\end{array}$

For the sake of completeness it should be noted that the norm minimization of ∥e∥ and ∥x∥ of Eqs. (3.6), (3.12), respectively, can be performed by the extended vector norms, where a norm of a vector w is defined as w^TQw and Q is a compatible positive definite weighting matrix. By doing so, one can choose the relative emphasis of the magnitudes of the vector components that is minimized.

For case A, Eq. (3.6) becomes

$\begin{array}{l}\hfill z=e^{T}Qe={(y-Ax)}^{T}Q(y-Ax)\end{array}$

with the solution

$\begin{array}{l}\hfill x={(A^{T}QA)}^{-1}{A}^{T}Qy.\end{array}$

From case B, Eq. (3.12) becomes

$\begin{array}{l}\hfill H=\frac{1}{2}{x}^{T}Qx+{\lambda }^T(y-Ax)\end{array}$

with the solution

$\begin{array}{l}\hfill x=Q^{-1}{A}^T{(A{Q}^{-1}{A}^T)}^{-1}.\end{array}$

In summary, a unified framework has been presented showing that the generalized inverse of a matrix can be viewed as a result of a minimization problem leading to a practical interpretation.

3.3.1 The solution to the compatible linear equations

We have the following general solution of a given linear matrix equation, which is formulated in terms of the Moore-Penrose inverse.

In particular, when b = 0, we obtain the general solution of the homogeneous linear equations Ax = 0 given by

$\begin{array}{l}\hfill x=(I_n-A^{+}A)t(\forall t\in C^n).\end{array}$

3.3.2 The least square solution of incompatible equation

Considering in many applications, such as data processing, multivariate analysis, optimization theory, modern control theory, and networking theory, the mathematical model of linear matrix equation is often an incompatible one. We hereafter use the generalized inverse matrix to represent the following general solution of incompatible linear equations.

3.3.3 The minimum norm least squares solution for the equations

From the above discussions, whether the equations are compatible or not, the least-square solutions can be expressed as

$\begin{array}{l}\hfill x^{*}=A^{+}b+(I_n-A^{+}A)t(t\in C^n).\end{array}$

Because the least squares solution is not unique, one is able to find a least square solution of minimum norm, which is given by

$\begin{array}{l}\hfill \parallel x^{**}{\parallel }_2=min\{\parallel x^{*}{\parallel }_2:x^{*}=A^{+}b+(I_n-A^{+}A)t,t\in C^n\},\end{array}$

where x** is referred to as the very minimal norm least square solution to the equations Ax = b. We have the following theorem: