6.6. Analysis in the Presence of Covariates
In many biological, medical and industrial applications, we often come across repeated measures data along with covariates that influence the response variable. It is important to account for the effects of such covariates. In clinical trials, the baseline measurements can be thought of as the useful covariates for analyzing response patterns at successive visits. For example, in therapies for the treatment of chronic stable angina, treadmill walking time (a covariate) is recorded just before the administration of a dose, and then at some post-dose times. The effectiveness of the visit doses is evaluated relative to the corresponding baseline walking times (Patel, 1986). Here the covariate information available for each person remains unchanged during the trial.
In Chapter 5 (Section 5.5) two types of covariates, viz. fixed over time and varying over time, were discussed and the analyses of repeated measures data with the covariates fixed over time were shown using both the multivariate and univariate approaches. These approaches make the assumption of either no covariance structure whatsoever (for multivariate approach) or the simplistic assumption of compound symmetry (for univariate approach). Both of these approaches fail when the correlation structure is not one of the two extremes or when the data are unbalanced along the time axis. We will now explore the analysis of covariance problem in the presence of various other covariance structures.
6.6.1. Covariates Fixed Over Time
Let yiju represent the observed value of the response variable on the uth subject from the ith treatment group at the jth occasion and xiu be an observed value of a covariate which may depend on the subject but does not depend on time. As a first step towards the analysis consider the model
where ϵiu=(ϵilu,...,ϵipiuu′ are independently distributed as piu-variate normal with mean vector zero and variance covariance matrix σ2Riu. If needed, these variance covariance matrices can be allowed to be different for different treatment groups, but their apparent dependence on U (that is, Riu depending on the uth subject) is only due to the fact that the dimensions of Riu, may be different for different subjects. Let us assume for the moment that they do not differ for different groups. Then the matrices Riu themselves will not be completely different, and will just be submatrices of a matrix, say Rmax, which corresponds to the (possibly hypothetical) subject with repeated measures at all time points. For example, suppose corresponding to this possibly hypothetical subject the error vector has a compound symmetric structure. That is, Rmax= (1−ρ)I+ρ11′. Then any matrix Riu will be a submatrix of this and will (still) depend on only two parameters.
The model considered above may appear rather general and complex. However, to account for various effects we do need to consider this model, at least in the initial stages of model building. We will first provide a brief explanation of the terms in the model. The term αi represents the effect of the treatment group, βj the effect of time, (αβ)ij the interaction effect between the variables, the treatment and time. The term λ xiu is considered to represent the common slope Λ of the line relating covariate to the response variable. The terms λj xiu and δi xiu respectively represent different slopes at different occasions and different slopes at different treatment groups respectively. Finally the term ηij xiu represents the interaction effects between the variables representing the treatment group, the time or occasion, and the covariate. In other words, the statistical significance of the term ηij implies that the slopes of the lines relating xiu to yiju are different for different levels of the treatment and time.
Noting D(yiu)=σ2Riu, where yiu=(yi1u,...,yipiuu)′, we can express the above model as
where y=(y11′,...,y1n1′,...,yk1′, ...,yknk′)′, and ϵ is similarly defined, β=(μ,α1,...,αk,β1,.....)′ is the vector of the parameters in the model, X is the appropriately chosen design matrix, and ϵ ~ Nn(0,σ2R), where R=diag(R11,...,Rknk, and 
. This model is a special case of the general linear mixed effects model when there are no random effects. Thus, the testing of linear hypotheses of the form H0:Lβ=0 for specific choices of matrix L can be easily carried out by appealing to the likelihood theory described earlier. If appropriate, a compound symmetric or any other alternative structures can be selected for Riu. To illustrate the analysis under this model we once again analyze the diabetic patients study data considered in Chapter 5, but with the aid of PROC MIXED.
EXAMPLE 6
Subject-specific Covariates, Diabetic Patients Study Data Three groups of diabetic patients, without complications (DINOCOM), with hypertension (DIHYPER), and with postural hypotension (DIHYPOT) respectively and a control (CONTROL) group of healthy subjects were asked to perform a small physical task at time zero. A particular response was observed at times −30, −1, 1, 2, 3, 4, 5, 6, 8, 10, 12, and 15 minutes. The responses at ten time points starting from 1 onward are denoted by Y1 through Y10 respectively. The corresponding subject specific covariates representing pre-performance responses (at times −30 and −1) are denoted by X1 and X2 and are used as covariates. The objective is to assess the group differences after correcting for the effects of covariates. We analyze these data using Program 6.6 under compound symmetry and AR(1) covariance structures. The corresponding output is presented in Output 6.6.
/* Program 6.6 */
options ls=64 ps=45 nodate nonumber;
title1 'Output 6.6';
data task;
infile 'task.dat';
input group$ x1 x2 y1-y10;
data a;
set task;
array t{10} y1-y10;
subject+1;
do time=1 to 10;
y=t{time};
output;
end;
drop y1-y10;
run;
proc mixed data=a method=reml covtest;
classes group time subject;
model y=group time time*group x1 x2 time*X1 time*X2 group*X1
group*X2 time*group*X1 time*group*X2;
repeated /type=cs subject=subject r;
title2 'Analysis Under CS Covariance Structure';
run;
proc mixed data=a method=reml covtest;
classes group time subject;
model y=group time time*group x1 x2 time*X1 time*X2 group*X1
group*X2 time*group*X1 time*group*X2;
repeated /type=ar(1) subject=subject r;
title2 'Analysis Under AR(1) Covariance Structure';
run;Example 6.6. Output 6.6
Analysis Under CS Covariance Structure
Model Fitting Information for Y
Description Value
Observations 247.0000
Res Log Likelihood -365.546
Akaike's Information Criterion -367.546
Schwarz's Bayesian Criterion -370.390
-2 Res Log Likelihood 731.0924
Null Model LRT Chi-Square 32.5465
Null Model LRT DF 1.0000
Null Model LRT P-Value 0.0000Tests of Fixed Effects
Source NDF DDF Type III F Pr > F
GROUP 3 14 2.58 0.0953
TIME 9 113 2.08 0.0373
GROUP*TIME 27 113 5.51 0.0001
X1 1 14 3.89 0.0685
X2 1 14 240.25 0.0001
X1*TIME 9 113 1.53 0.1473
X2*TIME 9 113 13.87 0.0001
X1*GROUP 3 14 1.58 0.2390
X2*GROUP 3 14 14.16 0.0002
X1*GROUP*TIME 27 113 1.80 0.0178
X2*GROUP*TIME 27 113 20.91 0.0001
Analysis Under AR(1) Covariance Structure
Model Fitting Information for Y
Description Value
Observations 247.0000
Res Log Likelihood -350.808
Akaike's Information Criterion -352.808
Schwarz's Bayesian Criterion -355.653
-2 Res Log Likelihood 701.6169
Null Model LRT Chi-Square 62.0220
Null Model LRT DF 1.0000
Null Model LRT P-Value 0.0000
Tests of Fixed Effects
Source NDF DDF Type III F Pr > F
GROUP 3 14 2.95 0.0692
TIME 9 113 1.08 0.3859
GROUP*TIME 27 113 3.52 0.0001
X1 1 14 4.75 0.0469
X2 1 14 274.13 0.0001
X1*TIME 9 113 1.61 0.1218
X2*TIME 9 113 8.51 0.0001
X1*GROUP 3 14 1.62 0.2290
X2*GROUP 3 14 15.57 0.0001
X1*GROUP*TIME 27 113 1.05 0.4175
X2*GROUP*TIME 27 113 10.64 0.0001 |
From Output 6.6, we observe that under the TYPE=CS option, many interactions are found to be statistically significant. Specifically, at 5% level of significance, the interaction effects of X1*GROUP*TIME, X2*GROUP*TIME, X2*GROUP, X2*TIME, GROUP*TIME and the effects of TIME and X2 are significant.
Suppose instead of the compound symmetry covariance structure we use the autoregressive (AR(1)) structure for the error covariance. When the analysis is performed using the TYPE=AR(1) option, the TIME, X1*TIME, and X1*GROUP*TIME effects were found to be statistically not significant. Additionally the model appears to be more parsimonious in the sense that fewer significant effects are observed. This reveals that AR(1) structure was perhaps more appropriate and that in the analysis under CS structure many interactions with TIME were declared as statistically significant possibly due to misspecified covariance structure. The fact that AR(1) is more suitable is also evident from comparatively larger AIC (=-352.808) and BIC (=-355.653) values.
Assuming that the AR(1) structure is a reasonable choice for the variance covariance matrix of the error, we may conclude that the covariate X1 does not play any significant role in the model. Since the interaction between the covariate X2 and GROUP*TIME is significant (p value=0.0001) we suggest including all the terms in the model except of course those involving the covariate X1.
6.6.2. Time Varying Covariates
In many repeated measures studies, the covariates themselves may vary over time and so in addition to being subject specific, they may also be time specific. In the medical field we often come across repeated measures data with covariates that influence the response variable at every time period where the measurements are made. For example, the effectiveness of a drug in the treatment of arteriosclerosis is probably influenced by many factors such as diet, exercise and smoking (Patel, 1986) which can be viewed as the covariates. In this situation the value of a covariate is being measured at each time point along with the response variable leading to what are termed as the time varying covariates.
Assume for simplicity that there is only one covariate, represented by x. The data in this case can be represented by yiju, xiju, j = 1,...,p (time periods), u=1,...,ni, i = 1,...,k (treatment groups). We also assume that there are no missing data for any time point. Then the following multivariate approach has been suggested by Patel (1986).
The multivariate approach
Let yiu be a p × 1 vector of responses and Xiu be p × 1 vector of the corresponding values of the covariate, taken over p occasions on the jth individual. Define yn×p =(y11:...:y1n1:y21:...:y2n2:...:yknk)′, n=
and Xn×p =(X11,:...:X1n1:X21:...:X2n2:...:Xknk)′. Then consider the following model similar (but not the same) as that in Equation 4.7,
Here A is a design matrix, 
is a matrix of unknown parameters, Γ is a diagonal matrix with the unknown diagonal elements, γ1,...,γp, representing the slopes of the line relating the covariate and the response variable at the time points 1,..., p respectively. The matrix ɛ is an n× p error matrix, rows of which are assumed to be independently distributed with a common multivariate normal distribution that has a zero mean vector and a p × p covariance matrix V. Note that the model (6.8) is still different from the usual multivariate analysis of covariance model discussed in Chapter 4 in the sense that its parameter matrix Γ is known (to be zero) except at the diagonal entries. This case of a partially known and partially unknown parameter matrix makes it harder to handle the analysis of this model in a routine MANOVA setup.
Patel (1986) provided an iterative algorithm describing the computation of the maximum likelihood estimators of the unknown parameters and for the likelihood ratio test for any general linear hypothesis of the form H0:
. It can be shown that the likelihood function under model (6.8) is
where 
The maximum likelihood estimators of 
and Γ are obtained by minimizing 
. The reason for this is that, if 
and Γ are known then the MLE of V is 
. Substituting this, the log-likelihood function reduces to 
apart from a constant. Hence the computation procedure iterates between computing 
as 
and estimating 
by minimizing 
with respect to 
and Γ. Thus,
where 
and 
are the estimated values of 
and Γ at the particular iteration. It can be shown that 
and Γ are respectively estimated from the equations
and
which together imply,
Based on this fact, Patel (1986) suggests the following iterative steps to solve the ML equations:
Initially take
=I and compute 
from (6.12).Compute
from (6.11).Compute
using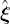 
and 
from (6.12). Then compute 
.Compute a revised estimate
from (6.12) using 
obtained in Step 3.Repeat Steps 2, 3 and 4 until the convergence has been obtained up to a desired degree of accuracy under a suitable convergence criterion.
This iterative scheme was initially implemented using the IML procedure by S. Rao (1995) for a data set provided by Dr. Barbara Hargrave of Old Dominion University. A cosmetically improved version is presented here as Program 6.7.
Suppose it is of interest to test for the significance of the covariate X. For this, we also need to estimate the parameters of the reduced model under H0: Γ=0. Under H0 we have the usual multivariate linear model, yn×p=An×p
. Hence the likelihood ratio test for testing the significance of the covariate can be easily constructed as described earlier.
To test a general linear hypothesis H0:LξM=0, Patel (1986) provides a similar algorithm for computing the ML estimates under the null hypothesis H0:LξM=0. As before, using the maximum likelihood estimates under no restriction and those under the null hypothesis, the likelihood ratio test for H0 can be obtained.
Under no restrictions on the parameters, the maximum of the likelihood can be shown to be
where 
is the maximum likelihood estimator of V. Similarly, the maximum likelihood estimator of V under H0, is ~ V, where 
. The maximum of L under H0:LξM=0 is
Thus, by taking the ratio of the quantities in Equations 6.14 and 6.13, the likelihood ratio test for testing H0:LξM=0 rejects the null hypothesis if
where Cα is a constant satisfying Pr(λ ≤ Cα |H0)=α. Using the standard likelihood theory, under H0, the quantity −2 ln,Λ asymptotically follows a chi-square distribution with mp−bc degrees of freedom.
Patel's approach has been illustrated through the following example.
EXAMPLE 7
Time Varying Covariates, Sheep Data The effects of phenylephrine induced increase in arterial pressure on the secretion of atrial natriuretic peptide (ANP) in the ovine fetus have been studied by Hargrave and Castle (1995). A set of 10 chronically cannulated fetal sheep was divided into two groups, the young and old. Arterial pressure was increased by infusing phenylephrine to the fetus from each of the two groups. Systematic mean arterial pressure (MAP), plasma ANP concentrations and plasma renin activity (PRA) were measured at three time points (5 min, 15 min, and 30 min) after infusion. PRA is used as the response variable and MAP is an accompanying time varying covariate. In our case, k=2, p=3, n1=6 and n2=10 and one covariate. The data set (SHEEP DATA) and the program appear in Program 6.7.
/* Program 6.7 */
option ls=64 ps=45 nodate nonumber;
title1 'Output 6.7';
title2 'Multivariate Analysis of Time Varying
Covariates Data';
proc iml;
y={66 59 47 −16 -29 6.9 −16
29 5.8 −40 -80 13 −1.6 60
16 −17,
−12 59 6.7 2.6 -53 -29 2.6
−40 -29 -60 170 −45 4.1 6.6
-73 -38,
60 46 6.7 −18.4 -61 -35 −18.4
-38 5.8 -58 80 -25 -7.1 0.2
−41 -50};
a={1 1 1 1 1 1 0
0 0 0 0 0 0 0
0 0,
0 0 0 0 0 0 1
1 1 1 1 1 1 1
1 1};
x1={135 21 55 22 -22 7.6 55
875 23 86 -9.6 −16 46 31
15 13,
545 97 78 -28 155 169 158
158 56 121 2.4 0.2 104 81
85 54,
840 224 210 -33 629 754 133
133 177 82 76 −16 25 442
830 205};
/* Enter the parameters for each problem */
n=16;
p=3;
eps=10;* Computation of gamma hat;
z=block(y, x1);
g=i(n)-(a`*inv(a*a`)*a);
* Initial value of Vhat;
nvhat=i(p);
do iteratio=1 to 50 while (eps > 0.0001);
vhat=nvhat;
pihat=log(det(vhat));
vhatinv=inv(vhat);
w=vhatinv#(y*g*X1`);
T=vhatinv#(x1*g*X1`);
onep=j(1,p,1);
gamma=onep*W*inv(T);
* Computation of xihat;
irp=repeat(i(p), 1, 2);
icn=i(n) // -i(n);
* Compute ygx= Y-Sum(Gamma*X);
gone=onep || gamma;
irpp=irp*diag(gone);
ygx=irpp*z*icn;
xihat= ygx*a`*inv(a*a`);
* Compute new Vhat and new pihat;
nvhat=(ygx-xihat*a)*(ygx-xihat*a)`;
npihat=log(det(nvhat));
eps=abs(pihat-npihat);
end;
* keep vhat for the computation of lambda;
vhat=nvhat;
print vhat;
/* Compute Vhat under the null hypothesis of
no covariate effect (we called this value sighat).
We have used PRINTE option of MANOVA statement of
PROC GLM for getting this value. These statements
are commented out in the program */
/*
yt=y`;
at=a`;
var1=({y1 y2 y3});
var2=({a1 a2});
create ndata1 from yt [colname=var1];
append from yt;
close ndata1;
create ndata2 from at [colname=var2];
append from at;
close ndata2;
data ndata;
merge ndata1 ndata2;
proc glm data=ndata;
model y1 y2 y3=a1 a2/noint nouni;
manova/printe;
*/
sighat={21554.744333 -8727.857667 3420.5183333,
-8727.857667 49988.409333 29065.183333,
3420.5183333 29065.183333 25186.393333};
* Test for testing no covariate effect;
lambda1=(det(vhat*inv(sighat)))**(n/2);print lambda1;
chi1=-2*log(lambda1);
print chi1;
pval1=1−probchi(chi1,3);
print pval1;
* Test of hypothesis: No time effect, algorithm;
/* Give L and M matrices */
L=i(2);
M={ 1 −1 0, 1 0 −1};
eps=10;
/* Use nvhat and gamma from the previous step as initial
values. So initial value of ygx=Y-Sum(Gamma*X) is also from
the previous step */
do iter=1 to 50 while (eps > 0.0001);
pihat=log(det(nvhat));
delta=2*inv(m*nvhat*m`)*(m*ygx*a`*inv(a*a`)*l)*
inv(l`*inv(a*a`)*l);
* Compute xi-tilde;
xtilde=(ygx*a`−0.5*nvhat*m`*delta*l`)*inv(a*a`);
vtilde=(ygx-xtilde*a)*(ygx-xtilde*a)`;
vtnv=inv(vtilde);
W=vtnv#(y*g*X1`);
T=vtnv#(x1*g*X1`);
onep=j(1,p,1);
gmt=onep*W*inv(T);
/* Update ygx=Y-Sum(gmt*X) in preparation for the next
iteration irp and icn are defined earlier */
icn=i(n) // -i(n);
gtn=onep || gmt;
irpp=irp*diag(gtn);
ygx=irpp*z*icn;
npihat=log(det(vtilde));
eps=abs(pihat-npihat);
nvhat=vtilde;
end;
print vtilde;
lambda=(det(vhat*inv(vtilde)))**(n/2);
print lambda;
chi=-2*log(lambda);
print chi;
pval2=1−probchi(chi,2);
print pval2;
quit;In Program 6.7 we first test for the significance of the covariate in the model. The unrestricted ML estimates of 
is found to be
Under the null hypothesis of no covariate effect, the ML estimate 
of 
=nV is the same as that obtained from the standard multivariate regression model. This estimate is obtained by using PROC GLM in Program 6.7 and is denoted as SIGHAT in the program. The complete output however is not shown. The results for the hypothesis test extracted from the output are summarized below:
Since the p value is smaller than 0.05 we conclude that the covariate effect is statistically not significant at a 5% level of significance.
In Program 6.7 we also provide PROC IML code for computing the likelihood ratio for the null hypothesis of no time effect. The corresponding null hypothesis
or
This can be written as H0: LξM=0 with L=I2×2 and
The ML estimate 
=nV under this null hypothesis is given by
Accordingly from Equation 6.15 the value of λ is 0.0025. Thus, −2 ln λ = 11.9920, which is statistically significant with the corresponding p value of 0.0025. The program can be appropriately modified to test other relevant linear hypotheses of interest with the appropriate choices of L and M. We summarize the results below for three such hypotheses of interest.
Using a univariate approach, Verbyla (1988) points out that model in Equation 6.8 can be expressed as Zellner's seemingly unrelated regression (SUR) model and a two-stage estimation procedure can be utilized. This method and its variations are discussed in detail using IML procedure by Timm and Mieczkowski (1997). We will not discuss these here.
A General Linear Model Approach
The multivariate approach described above cannot handle unbalanced data and ignores any observations with missing values. An alternative univariate approach which can handle the unbalanced data will be described below (Rao, 1995).
Let 1×p vector yi′ be the ith row of y, i = 1,...,n in the model given in Equation 6.8 assuming only one treatment group (that is, k=1) for illustration. Similarly consider other vectors and matrices of model Equation 6.8. Then tentatively assuming no missing values, we can write the model from Equation 6.8 as,
where ai′ is the ith row of matrix A and other quantities are similarly defined. Transposing both sides, we obtain
where Ai=diag(ai′,...,ai′), Di=diag(x1i,..., xpi, η′=[ξ1′,..,ξp′], and γ′=(γ1,..., γp).
The above equation can again be rewritten in the form
or
where Bi=[Ai : di], and 
Let y=(y1′,...,yn′)′ and 
. Then
or
which is a special case of linear model in the Equation 6.1 with no random effects and D(ϵ)=σ2R=σ2In⊗V(θ), where V(θ) is a p×p variance covariance matrix of the repeated measures depending on a vector of parameters θ, and B=(B1′,...,Bp′)′. It may be noted that although we have presented here the model with no missing covariates, the only change, were there any missing covariate values at any time points for a particular subject, will be to discard the particular values of the dependent variable (corresponding to the particular time points only and, only for the particular subject). This model, being a special case of a general mixed effects linear model, can be analyzed using the MIXED procedure. For illustration, we consider the following example.
EXAMPLE 7
Sheep Data (continued) To illustrate, we again consider the SHEEP DATA where k=2, p=3, n1=6 and n2=4 and there is one covariate, namely MAP. The SAS code to analyze these data under a general linear model using PROC MIXED is given in Program 6.8 and the corresponding output is presented in Output 6.8.
/* Program 6.8 */
options ls=64 ps=45 nodate nonumber;
title1 'Output 6.8';
title2 'Analysis of Time Varying Covariates Data';
title3 'Analysis with Independent Error for Subjects';
data one;
infile 'sheep.dat';
input group$ sheep time pra anp map;data one;
set one;
y=pra;
x=anp;
z=map;
run;
proc mixed data=one method=reml;
classes group time sheep;
model y=group time group*time time*z group*z group*time*z z;
repeated /type=simple subject=sheep r;
run;
title3 'Analysis with Compound Symmetry Error for Subjects';
proc mixed data=one method=reml;
classes group time sheep;
model y=group time group*time time*z group*z group*time*z z;
repeated /type=cs subject=sheep r;
run;Example 6.8. Output 6.8
Analysis of Time Varying Covariates Data
Analysis with Independent Error for Subjects
The MIXED Procedure
Class Level Information
Class Levels Values
GROUP 2 old young
TIME 3 5 15 30
SHEEP 10 24 49 502 505 528 599 617 618
717 722
REML Estimation Iteration History
Iteration Evaluations Objective Criterion
0 1 195.78315742
1 1 195.78315742 0.00000000
Convergence criteria met.
R Matrix for SHEEP 24
Row COL1 COL2 COL3
1 1091.5163360
2 1091.5163360
3 1091.5163360
Covariance Parameter Estimates (REML)
Cov Parm Subject Estimate
DIAG SHEEP 1091.5163360Analysis with Independent Error for Subjects
Model Fitting Information for Y
Description Value
Observations 30.0000
Res Log Likelihood −114.432
Akaike's Information Criterion −115.432
Schwarz's Bayesian Criterion −115.878
-2 Res Log Likelihood 228.8649
Null Model LRT Chi-Square 0.0000
Null Model LRT DF 0.0000
Null Model LRT P-Value 1.0000
Tests of Fixed Effects
Source NDF DDF Type III F Pr > F
GROUP 1 8 4.84 0.0590
TIME 2 10 0.89 0.4394
GROUP*TIME 2 10 0.28 0.7612
Z*TIME 2 10 0.84 0.4596
Z*GROUP 1 10 0.26 0.6231
Z*GROUP*TIME 2 10 1.63 0.2444
Z 1 10 2.30 0.1600
Analysis with Compound Symmetry Error for Subjects
The MIXED Procedure
Class Level Information
Class Levels Values
GROUP 2 old young
TIME 3 5 15 30
SHEEP 10 24 49 502 505 528 599 617 618
717 722
REML Estimation Iteration History
Iteration Evaluations Objective Criterion
0 1 195.78315742
1 2 182.64116970 0.00035155
2 1 182.60566734 0.00001167
3 1 182.60457671 0.00000002
4 1 182.60457534 0.00000000
Convergence criteria met.R Matrix for SHEEP 24
Row COL1 COL2 COL3
1 1067.2157907 865.09810940 865.09810940
2 865.09810940 1067.2157907 865.09810940
3 865.09810940 865.09810940 1067.2157907
Covariance Parameter Estimates (REML)
Cov Parm Subject Estimate
CS SHEEP 865.09810940
Residual 202.11768133
Analysis with Compound Symmetry Error for Subjects
Model Fitting Information for Y
Description Value
Observations 30.0000
Res Log Likelihood −107.843
Akaike's Information Criterion −109.843
Schwarz's Bayesian Criterion −110.734
-2 Res Log Likelihood 215.6864
Null Model LRT Chi-Square 13.1786
Null Model LRT DF 1.0000
Null Model LRT P-Value 0.0003
Tests of Fixed Effects
Source NDF DDF Type III F Pr > F
GROUP 1 8 4.72 0.0615
TIME 2 10 6.08 0.0187
GROUP*TIME 2 10 0.38 0.6907
Z*TIME 2 10 3.16 0.0862
Z*GROUP 1 10 1.87 0.2014
Z*GROUP*TIME 2 10 2.67 0.1179
Z 1 10 0.06 0.8110 |
We assume the compound symmetric error structure and, thus, perform the analysis with the TYPE = CS option in the REPEATED statement. From the output the estimated compound symmetry correlation coefficient is equal to 
=865.0981/1067.2158= 0.8106. Further, from the bottom part of the output (under `Tests of Fixed Effects') we conclude that only the TIME factor is statistically significant at a 5% level of significance. This agrees with our earlier conclusion arrived at by using the multivariate approach, except that the covariate effect was also significant in the multivariate approach.
It may be emphasized that if time varying covariates are present then the estimates and the tests under the options TYPE=CS and TYPE=SIMPLE will be different (compare the two sets of outputs given above corresponding to these options). This is in stark contrast from the situation of subject specific covariates. This is so because in the former situation, the generalized least squares estimators, with the compound symmetry covariance structure for the error, are not the same as the ordinary least squares estimators.