3.4. ANOVA Partitioning

In the multivariate context, the role of the total sum of squares is played by the p by p positive definite matrix of (corrected) total sums of squares and crossproducts (SS&CP) defined as

Apart from the dividing factor, a typical element of the matrix in Equation 3.6, say the one corresponding to the i^th row and j^th column, is the same as the sample covariance between the i^th and j^th dependent variables. Consequently, the diagonal elements of T are the (corrected) total sums of squares for the respective dependent variables.

Assuming that Rank(X) = k + 1, this matrix can be partitioned as the sum of the two p by p positive definite matrices

where

and Ŷ = X is the matrix of the predicted values of matrix Y. The matrix R represents the matrix of model or regression sums of squares and crossproducts, while the matrix E represents that corresponding to error. Note that the diagonal elements of these matrices respectively represent the usual regression and error sums of squares for the corresponding dependent variables in the univariate linear regression setup.

Table 3.1 summarizes the partitioning explained above, along with a similar partitioning for the degrees of freedom (df).

An unbiased estimator of Σ is given by

Table 3.1. Multivariate Analysis of Variance (Manova)

Source	df	SS & CP	E(SS & CP)
Regression Error	k n − k − 1	RE
Corrected Total	n−1	T

When X is not of full rank, (X′X)⁻¹ is replaced by (X′X)⁻, a generalized inverse of (X′X) in the formulas in Equations 3.7 and 3.8, but the matrices R, E and Ŷ are invariant of the choice of a particular generalized inverse and remain the same regardless of which generalized inverse is used. However, in this case the unbiased estimator of Σ is given by E/(n − Rank(X)), which differs from Equation 3.9 in its denominator.

Depending on the rank of R, the matrix R can further be partitioned into two or more positive definite matrices. This fact is useful in developing the tests for various linear hypotheses on B. If needed, for example, as in the lack-of-fit analysis, a further partitioning of matrix E is also possible.

The matrix R, of regression sums of squares and crossproducts, measures the effect of the part of the model involving the independent variables. By contrast, E, the error sums of squares and product matrix, measures the effect due to random error or the variation not explained by the independent variables. Further partitioning of R and E can also be given certain similar interpretations.

In univariate regression models, the coefficient of determination R², which is the ratio of regression sum of squares to total sum of squares, is taken as an index to measure the adequacy of the fitted model. Analogously, in the present context, it is possible to define

and

as two possible generalizations of R². In the hypothesis testing context, the latter measure is often referred to as Pillai's trace statistic. These indices can be interpreted in essentially the same way as the univariate coefficient of determination R².

Another useful measure of the strength of the relationship or the adequacy of the model can be defined as 1 − |E| / |R + E| = 1 − Λ, where Λ = |E| / |R + E| is called the Wilks' ratio. However, this index of association is strongly biased. Jobson (1992) provides two modifications of 1 − Λ, one of which has considerably less bias while another provided by Tatsuoka (1988) is approximately unbiased. These are respectively given by

and

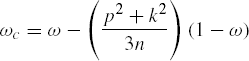
As the value of Λ is produced by several SAS procedures performing multivariate analyses, these two measures are easily computable. It may be remarked that ω and ω_c can be negative.