4.1. Introduction

In the previous chapter, we considered the multivariate linear regression model

In the model, the

• n by p matrix Y contains the random observations on p dependent variables,

• k + 1 by p matrix B is the matrix of unknown parameters,

• n by p matrix ε is the matrix of random errors such that each row of ε is a p variate normal vector with mean vector zero and variance-covariance matrix Σ. The matrix Σ is assumed to be a p by p positive definite matrix.

• n by k + 1 matrix X was assumed to be of full rank, that is, Rank(X) = k + 1.

There are, however, situations especially those involving the analysis of classical experimental designs where the assumption Rank(X) = k + 1 cannot be made. This in turn requires certain suitable modifications in the estimation and testing procedures. In fact, following the same sequence of development as in the previous chapter, a generalized theory has been developed, which contains the results of the previous chapter as the special "full rank" case.

Let us assume that Rank(X) = r < k + 1. It was pointed out in Chapter 3 that in this case, the solution to the normal equations in Equation 3.3 is not unique. If (X′X)⁻ is a generalized inverse of X′X, then correspondingly a least square solution is given by

which will depend on the particular choice of the generalized inverse. As a result, the matrix B is not (uniquely) estimable. The following example illustrates this case.

EXAMPLE 1

Checking Estimability, Jackson's Laboratories Comparison Data Jackson (1991) considered a situation where samples were tested in three different laboratories using two different methods. Each of the laboratories received four samples and each of the samples was divided into subsamples to be tested by these two methods. As a result, the observations on the subsamples arising out of the same sample are correlated leading to the data as the four bivariate vector observations per laboratory. The data are shown in Table 4.1.

Table 4.1. Laboratory Data

Laboratory	Method 1	Method 2
1	10.1	10.5
	9.3	9.5
	9.7	10.0
	10.9	11.4
2	10.0	9.8
	9.5	9.7
	9.7	9.8
	10.8	10.7
3	11.3	10.1
	10.7	9.8
	10.8	10.1
	10.5	9.6

Let y_ij be the 2 by 1 vector of observation on the j^th sample sent to the i^th laboratory, j=1,...,4; i = 1,2,3. If we assume that y_ij has a bivariate distribution with a structured mean vector 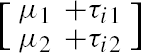and the variance covariance matrix Σ, then we can write our model as

Stacking these equations one below the other for j=1,...,4 and (then for) i = 1,2,3, leads to

where represents the sample-to-sample variation. The model represented by the set of equations given above is in the form of Equation 4.1, with

where 1_q represents a q by 1 vector of unit elements. Since all the elements of X are either zero or one, with zero representing the absence and one representing the presence of the particular parameter in the individual equation, this can be considered as a situation where the regression is performed on the dummy variables. It is easy to see that since the last three columns of the matrix X above add to the first column, the first column is linearly dependent on the last three columns. A similar statement can be made about the linear dependence of any other columns on the remaining three. As a result, the matrix X is not of full column rank. In fact, Rank(X) = 3, as the last three columns of X form a linearly independent set of vectors. Now as Rank (X′X) = Rank (X) = 3, the 4 by 4 matrix X′X is singular, thereby not admitting the inverse (X′X)⁻¹. Therefore the least squares system of linear equations corresponding to Equation 4.1,

does not admit a unique solution . As a result, for k = 1,2, (μ_k, τ_1k, τ_2k, τ_3k) cannot be uniquely estimated.

If we want to estimate the mean measurement for each of the two methods, then the quantities of interest are v_ik = μ_k +τ_ik, i = 1,2,3, k = 1,2. We may also be interested in comparing the laboratories, that is, in estimating the differences between the true means for the three laboratories, namely v_1k - v_2k = τ_1k - τ_2k, v_1k - v_3k = τ_1k - τ_3k and v_2k - v_3k = τ_2k - τ_3k, k = 1, 2.. Even though (μ_k, τ_1k, τ_2k, τ_3k) cannot be uniquely estimated, the unique estimates of these differences are available, regardless of what generalized inverse is used to obtain the solution (), k = 1,2 of X′XB=X′Y. Thus, even though the matrix B is not estimable, certain linear functions of B are still estimable. Specifically, as mentioned in Chapter 3, a nonrandom linear function c′B, where c ≠ 0 is estimable if and only if

Quite appropriately, a linear hypothesis is called testable if it involves only the estimable functions of B.

For the first laboratory, the vector of mean measurements for each of the two methods (v₁₁, v₁₂) is given by

with c′=(1 1 0 0). The choices of respective c′ vectors for the other two laboratory means are obtained in the same way. These are (1;0;1;0) and (1;0;0;1). Similarly, for the differences between the laboratory means the three choices of c are

It can be theoretically shown (Searle, 1971) that all the above choices of c satisfy Equation 4.2 and hence all the laboratory means and their pairwise differences are estimable. It is equivalent to saying that all of the above choices of c′ can be expressed as the linear function of the rows of X. That this is true in our example is easily verified by the visual examination of the rows of our matrix X. The actual rank of the matrix X would depend on the particular design and the particular statistical model. For a one-way classification model with k groups, the rank of X_{n× (k+1)} is k. This deficiency in rank of X affects the tests for the statistical significance in many ways. First of all, such tests can be performed only for the testable linear hypotheses. That given, all the univariate and multivariate tests can still be adopted after making a simple yet important modification. When the hypothesis is linear, the quantity r = Rank(X) replaces (k+1) in most formulas of Chapter 3.