CHAPTER 11
Centroid and Moment of Inertia
Learning Objectives
11.1 INTRODUCTION
The centroid is the mean position of elements of area. The coordinates of centriod is mean value of coordinates of all the elemental points in the area. The center of mass is the mean position of elements of mass. In a uniform gravitational field, the gravitational force acts through the center of mass. But, if the gravitational field (hypothetically) is not uniform (in the case of very large body), center of mass and center of gravity will be different. Similarly, if the mass per unit area of a shape varies, the center of mass would not coincide with the centroid. Centroid is a mathematical, geometric concept, i.e., the geometric center of a body. It can be calculated as the center of mass of an object with constant density throughout density.
11.2 DETERMINATION OF POSITION OF CENTROID OF PLANE GEOMETRIC FIGURES
11.2.1 Center of Gravity, Center of Mass, and Centroid of an Irregular Shape
In Figure 11.1, an irregular shape is shown for which we want to calculate the center of gravity, the center of mass and centroid. Here, our purpose is to differentiate the concepts of these three different terms. It is assumed that the irregular shape, as shown in Figure 11.1, is of uniform thickness, density and subjected to the uniform gravitational field.
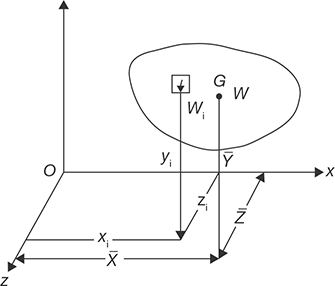
FIGURE 11.1
Center of Gravity, Center of Mass, and Centroid
Let Wi be the weight of an element in the given body. W be the total weight of the body. Let the coordinates of the element are Xi, Yi, Zi and that of centroid G be X̅, Y̅, and Z̅ . Since W is the resultant of Wi forces. Therefore,

Here, X̅, Y̅, and Z̅ are coordinates of the center of gravity, G. The resultant gravitational force acts through the point G.
If gravitational field be uniform, the gravitational acceleration (g) will be same for all the points. Therefore, in of Wi, we can put Mig and the center of mass can be expressed as:

Here, X̅, Y̅, and Z̅ are coordinates of the center of mass, G. The resultant mass of the body is concentrated at the point, G.
If the density of mass (γ) and the thickness of the body (t) is uniform, the mass Mi can be represented as γ · Ai · t. The centroid can be expressed as:
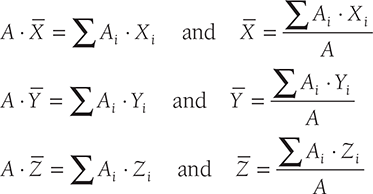
Here, X̅, Y̅, and Z̅ are coordinates of centroid, G.
11.2.2 Centroid of I-section
The I-section shown in Figure 11.2 can be divided into three parts; lower part of area A1, the middle part of area A2, and upper part of area A3. The lengths and widths of the all the parts of I-section are shown in the Figure 11.2. Let the X and Y coordinates be pass through origin O as shown in the Figure 11.3.
The coordinates for centroid can be calculated using the following formula:
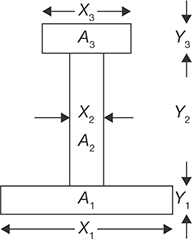
FIGURE 11.2
Centroid of I-section
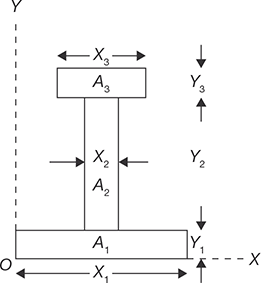
FIGURE 11.3
Reference Axes for I-section
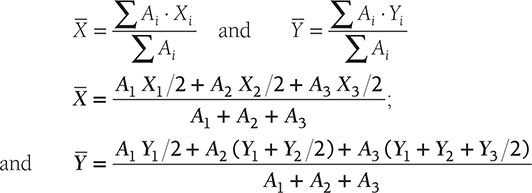
In the case of axial symmetry about Y-axis, the distances of X1/2, X2/2, X3/2 from origin will be zero.
Hence, X̅ = 0.
11.2.3 Centroid of U-section
The U-section shown in Figure 11.4 can be divided into three parts; lower part of area A1 and two upper parts of area A2. The lengths and widths of the all the parts of U-section are shown in the Figure 11.4. Let the X and Y coordinates be pass through origin o as shown in the Figure 11.4.
The coordinates for centroid can be calculated using the following formula:
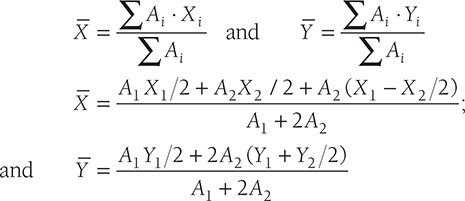
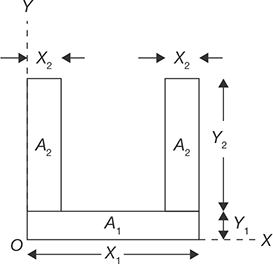
FIGURE 11.4
U-section
In the case of axial symmetry about Y-axis, the distances of X1/2, X2/2 from origin will be zero.
Hence, X̅ = 0.
11.2.4 Centroid of H-section
The H-section shown in Figure 11.5 can be divided into three parts; left and right parts of area A1 and central part of area A2. The lengths and widths of the all the parts of H-section are shown in the Figure 11.5. Let the X and Y coordinates be pass through origin 0 as shown in the Figure 11.5.

FIGURE 11.5
H-section
The coordinates for centroid can be calculated using the following formula:
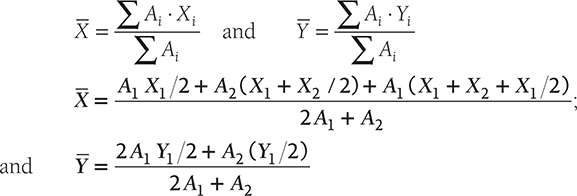
In the case of axial symmetry about Y axis, the distances of X1/2, X2/2 from origin will be zero.
Hence, X̅ = 0.
11.2.5 Centroid of L-section
The L-section shown in Figure 11.6 can be divided into two parts; Lower part of area A1 and upper part of area A2. The lengths and widths of the all the parts of L-section are shown in the Figure 11.6. Let the X and Y coordinates be pass through origin 0 as shown in the Figure 11.6.
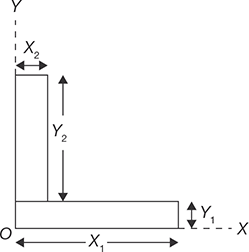
FIGURE 11.6
L-Section
The coordinates for centroid can be calculated using the following formula:
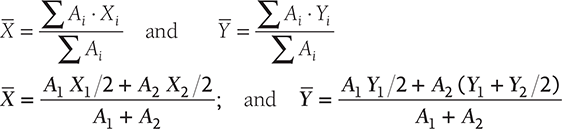
11.2.6 Centroid of T-section
The T-section shown in Figure 11.7 can be divided into two parts; Lower part of area A1 and upper part of area A2. The lengths and widths of the all the parts of L-section are shown in the Figure 11.7. Let the X and Y coordinates be pass through origin 0 as shown in the Figure 11.7.

FIGURE 11.7
T-Section
The coordinates for centroid can be calculated using the following formula:

11.2.7 Centroid of C-section
The C-section shown in Figure 11.8 can be divided into three parts; Lower and upper parts of area A1 and middle part of area A2. The lengths and widths of the all the parts of C-section are shown in the Figure 11.8. Let the X and Y coordinates be pass through origin 0 as shown in the Figure 11.8.
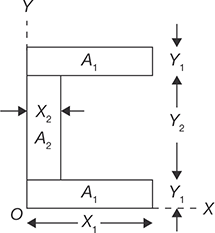
FIGURE 11.8
C-Section
The coordinates for centroid can be calculated using the following formula:
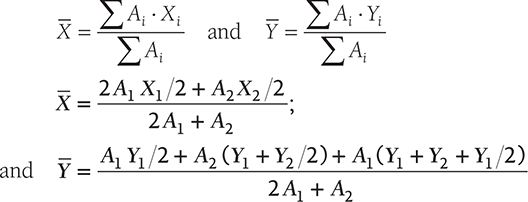
11.2.8 Centroid of Circular Arc
Centroid of an arc of a circle, as shown in Figure 11.9, has length L = R · 2α. Let us consider an element of the arc of length dL= Rdθ.
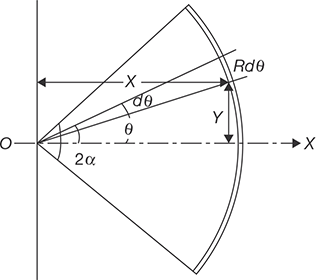
FIGURE 11.9
Centroid of Circular Arc

And

11.2.9 Centroid of Semicircular-section of a Disc
Considering a semicircle of radius R as shown in Figure 11.10. Due to symmetry centroid must lie on the y-axis. Let its distance from the x-axis be Y̅ . To find Y̅ , consider an element at a distance r from the center O of the semicircle, radial width dr and bound by radii at θ and θ + dθ.

FIGURE 11.10
Centroid of Circular Section of a Disc
Area of the element = rdθ dr.
its moment about x-axis is given by,
Total moment of area about x-axis,

Thus, the centroid lies on the y-axis at a distance of ![]() from the diametric axis.
from the diametric axis.
11.2.10 Centroid of a Sector of a Circular Disc
Consider a sector of a circular disc of angle 2α as shown in Figure 11.11. Due to symmetry, centroid ‘G’ lies on the x-axis. To find its distance from the center O, consider an elemental area as shown in the Figure 11.11.
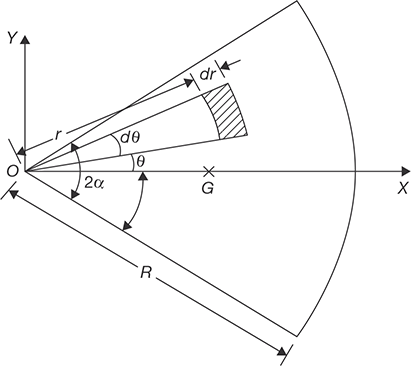
FIGURE 11.11
Centroid of a Sector of a Circular Disc
Moment of area of the element = rdθ × dr × r cos θ = r2 cos θ dr dθ
Total moment of area about y-axis

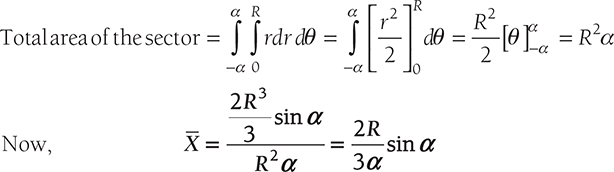
11.2.11 Centroid of a Parabola
Considering a parabolic section of height, h and base b. Now to find the centroid of this section, consider a small element of width dx at a distance of x from the origin O.


FIGURE 11.12
Centroid of a Parabolic Section

FIGURE 11.13
Centroid of a Triangle
11.2.12 Centroid of a Triangle
Consider a triangle ABC of the base, b and height, h. Let us locate the centroid of the triangle from its base. Let b1 be the width of an elemental strip of thickness dy at a distance y from the base. Since ΔAEF and ΔABC are similar triangles, therefore,
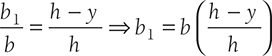
Area of element, 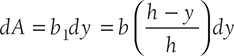
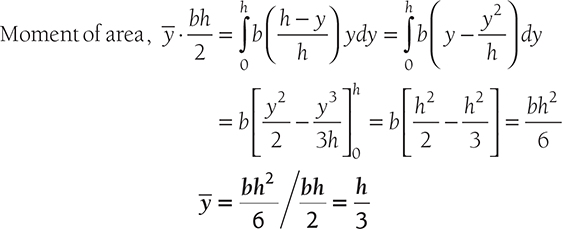
Thus the centroid of a triangle is at a distance h/3 from the base and 2h/3 from the apex where h is the height of the triangle.
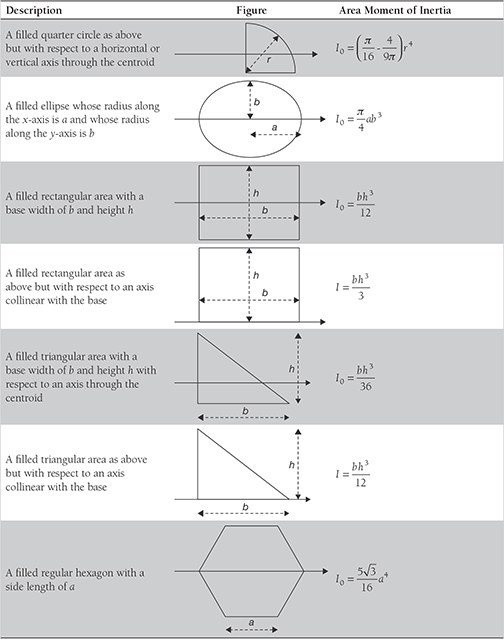
11.3 SECOND MOMENT OF AREA
The second moment of area is also known as area moment of Inertia. Consider a small lamina of area A. The second moment of area about x-axis or y-axis can be found by integrating the second moment of area of the small element of area dA of the lamina, i.e., ∫ x2dA or ∫ y2dA. The product of the area and square of the distance of the centroid from an axis is known as area moment of Inertia. Similarly, the product of area and distance of the center of gravity of a mass from an axis is known as mass moment of inertia.

FIGURE 11.14
A Plane Area for Analysis of the Second Moment of Area n
Consider a plane area which is divided into small areas A1, A2, …, An. Let the centroid of the small areas from a given axis be at a distance of r1, r2, …, rn respectively. The second moment of area can be given as
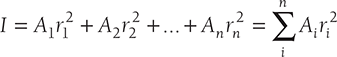
11.3.1 Radius of Gyration
Radius of gyration of a body about an axis is a distance such that its square multiplied by the area gives a moment of inertia of the area about the given axis.

11.3.2 Theorem of Perpendicular Axis
Theorem of perpendicular axis states that if IXX and IYY be the moment of inertia of a plane section about two mutually perpendicular axes X-X and Y-Y in the plane of the section (as shown in Figure 11.15), then the moment of inertia of the section IZZ about the axis Z-Z, perpendicular to the plane and passing through the intersection of axes X-X and Y-Y is given by
or, ![]()
Hence, IZZ is also known as polar moment of inertia.
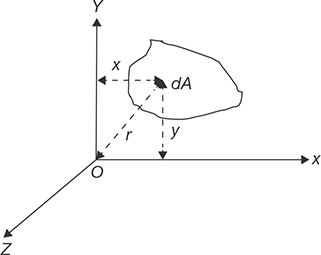
FIGURE 11.15
Perpendicular Axis Theorem
11.3.3 Theorem of Parallel Axis
Theorem of parallel axis states that if the moment of inertia of a plane area about an axis in the plane of the area through centroid be represented by IG, then the moment of inertia of the plane about a parallel axis AB (IAB) in the plane at a distance h from the centroid of the area is given by

FIGURE 11.16
Parallel Axis Theorem
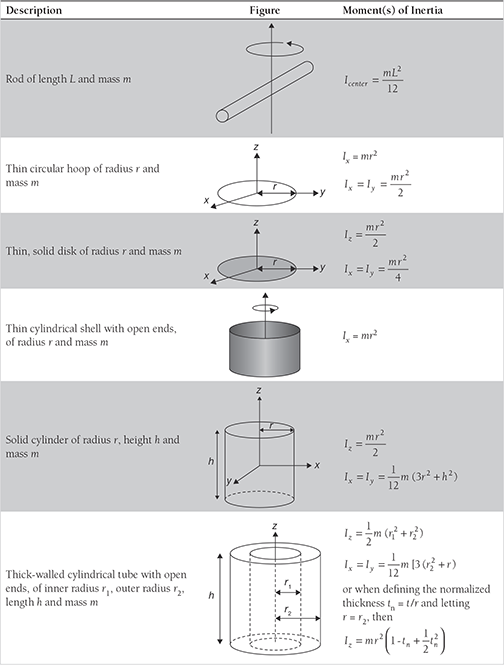
11.3.4 Moment of Inertia from First Principle
A. Moment of Inertia of a Rectangle
Consider an elemental strip of width dy at distance of y from a centroidal axis of a rectangle.
Moment of inertia of the strip is given by

FIGURE 11.17
Moment of Inertia of a Rectangle about Centroidal Axis
Now, Moment of Inertia of entire rectangle can be given by

B. Moment of Inertia of a Triangle
Consider an elemental strip of width dy at distance of y from the base of a triangle. Moment of inertia of the strip about its base is given by
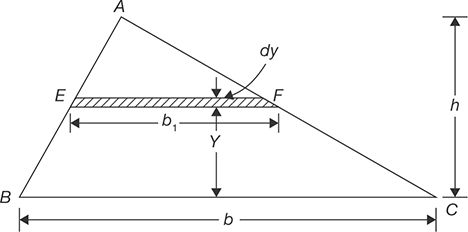
FIGURE 11.18
Moment of Inertia of a Triangle about its Base
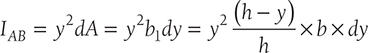
Now, moment of inertia of entire triangle about its base

C. Moment of Inertia of a Circular Disc
Consider an element of the arc length rdθ and width dr of the circular disc as shown in Figure 11.19. Now, the moment of inertia of the element about diametral axis x-x is given by
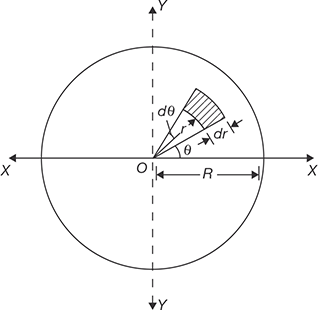
FIGURE 11.19
Moment of Inertia of a Circular Disc about its Diametral Axis
Now, moment of inertia of entire circle about diametral axis is given by

11.3.5 Moment of Inertia of Some Composite Sections
The composite section in the Figure 11.20 can be divided into three parts: triangular part of area A1; rectangular part of area A2; and semicircular part of area A3. The individual centroid for each section is shown in the figure 11.20 as C1, C2, and C3. The centroid of the entire section is located as C. Consider the moment of inertia of the sections 1, 2, and 3 about the axes parallel to XX and passing through their individual centroid are IC1, IC2, and IC3 respectively. The moment of inertia of the entire composite section about the axis XX passing through the centroid C can be given as
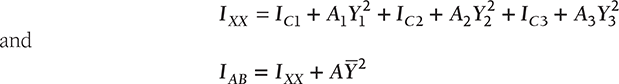
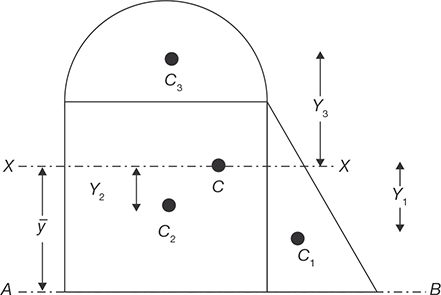
FIGURE 11.20
Moment of Inertia of a Composite Section
11.4 CENTER OF GRAVITY OF SOLIDS
Center of gravity of a solid is a point through which resultant line of forces passes or the line of action of gravity force passes. The difference between the center of gravity and centroid has been already explained in subsection 11.1.
11.5 MASS MOMENT OF INERTIA
Mass moment of inertia of a body about an axis is defined as the sum of the product of its elemental masses and square of their distances from the axis.
Radius of gyration of a solid body can be given as
 .
.where I is mass moment of inertia, M is the mass of the body, and k is the radius of gyration.
11.5.1 Mass Moment of Inertia of a Circular Ring
Consider a circular ring of radius R as shown in Figure 11.21. Let the mass per unit length of the ring is ‘m’. To find the mass moment of inertia of the ring about the diametral axis XX, consider an element of length ds = rdθ; the distance of the element from the diametral axis XX is R sinθ; and mass of the element is mrdθ.
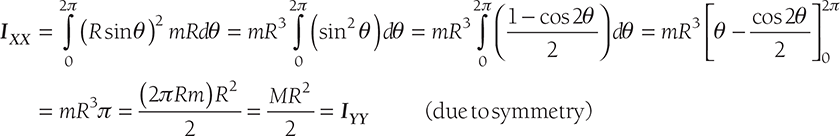
The moment of Inertia about an axis passing through the center of the circle and perpendicular to the plane of circular ring

FIGURE 11.21
Mass Moment of Inertia of a Circular Ring
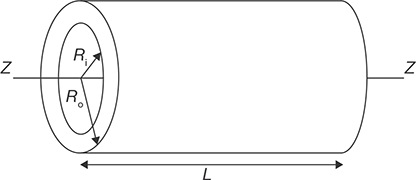
FIGURE 11.22
Mass Moment of Inertia of a Hollow Cylinder
11.5.2 Mass Moment of Inertia of a Circular Disc
Consider an element of the disc of arc length rdθ, width dr and thickness t. ρ is the mass density of the disc. Mass moment of inertia of the disc can be calculated as (refer Figure 11.19)
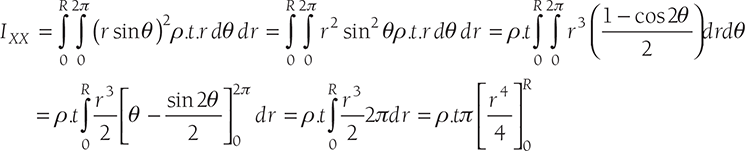


11.5.3 Mass Moment of Inertia of a Hollow Cylinder
Let in Figure 11.22, Ro = outer radius of cylinder; Ri = inner radius of the cylinder, L = length of cylinder; ρ = mass density of the cylinder; M = mass of the cylinder;.
Consider a small elemental ring of width dr at a distance of radius r from the center of cylinder then the mass of the element, dm = ρ. 2πr . dr · L
Now mass moment of inertia of the element about the axis ZZ
Moment of inertia of the cylinder about the axis ZZ
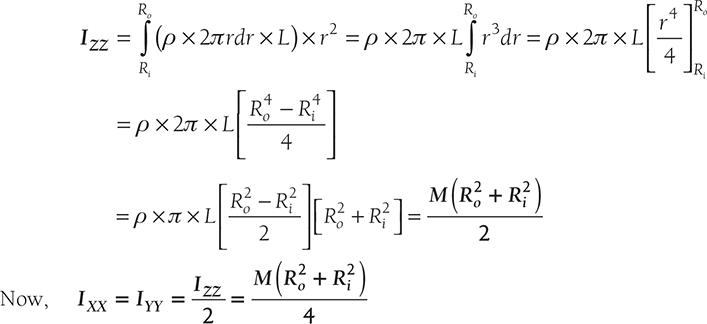
11.5.4 Mass Moment of Inertia of Sphere
Consider an elemental plate of thickness dy at a distance y from the diametral axis as shown in Figure 11.23. Radius of this elemental circular plate x is given by
Mass of the elemental plate, dm = ρπx2 dy = ρπ (R2 – y2) dy

FIGURE 11.23
Mass Moment of Inertia of Sphere
Moment of inertia of the plate element about axis

But, mass of sphere, 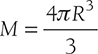
Massmoment of inertia of hemisphere about the axis ZZ,
Moment of inertia of the plate element about axis

11.5.5 Mass Moment of Inertia of a Circular Cone
Consider an elemental plate at a distance x from the apex of radius r and thickness dx. Mass of elemental plate = ρπr2dx
The moment of inertia of circular plate about normal axis through its center is

But, 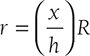
Moment of inertia of the elemental plate about the axis 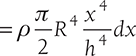
Moment of inertia of cone about its axis,
Mass of the cone, 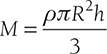
Moment of inertia of cone about its axis, ![]()
RECAP ZONE
Points to Remember
- The centroid is the mean position of elements of an area. The coordinates of the centroid are mean value of coordinates of all the elemental points in the area.
- The center of mass is the mean position of elements of mass. In a uniform gravitational field, the gravitational force acts through the center of mass. But, if the gravitational field (hypothetically) is not uniform (in the case of the very large body), the center of mass and center of gravity will be different.
- The centroid is a mathematical, geometric concept, i.e., the geometric center of a body. It can be calculated as the center of mass of an object with constant density throughout density.
- The second moment of area is also known as area moment of Inertia. Consider a small lamina of area A.
- The second moment of area about x-axis or y-axis can be found by integrating the second moment of area of small element of area dA of the lamina, i.e., ∫ x2dA or ∫ y2dA.
- The product of the area and square of the distance of the centroid from an axis is known as area moment of Inertia.
- The radius of gyration of a body about an axis is a distance such that its square multiplied by the area gives a moment of inertia of the area about the given axis.
- Theorem of perpendicular axis states that if IXX and IYY be the moment of inertia of a plane section about two mutually perpendicular axes X-X and Y-Y in the plane of the section, then the moment of inertia of the section IZZ about the axis Z-Z, perpendicular to the plane and passing through the intersection of axes X-X and Y-Y is given by
IZZ = IXX + IYY = ∫r2dA
- Theorem of parallel axis states that if the moment of inertia of a plane area about an axis in the plane of the area through centroid be represented by IG, then the moment of inertia of the plane about a parallel axis AB (IAB) in the plane at a distance h from the centroid of the area is given by IAB = IG + Ah2.
- Mass moment of inertia of a body about an axis is defined as the sum of the product of its elemental masses and square of their distances from the axis.
Important Formulae
REVIEW ZONE
Multiple-choice Questions
- Which of the following forms the basis of rigid bodies and strength of material?
- Centroid
- Center of gravity
- Moment of inertia
- Any of the above
- “The moment of inertia of a lamina about any
axis in the plane lamina equal the sum of the
moment of inertia about a parallel centroidal axis
in the plane lamina and the product of the area
of the lamina and square of the distance between
the two axes”.
The above theorem is known as
- Parallel axis theorem
- Perpendicular axis theorem
- Three-moment theorem
- None of the above
- Centroid of a circular arc of radius R including
angle 2α can be given by:
- Centroid of a semicircular disc or radius R can be
given as:
- Centroid of a sector of a circular disc of radius r
and included angle 2α can be given as:

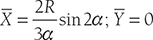
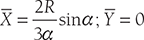
- X̅ = —sin2 ; Y̅ = 0
- Centroid of parabola of height h and base b
(y = k x2) can be given as:
- Radius of gyration of a body can be given as:
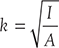


- Both (a) and (b)
- Moment of inertia of a triangle of base b height h about its base can be given as:
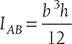
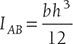

- None of these
- Moment of inertia of a triangle of base b height h about its center parallel to its base can be given



- None of these
- Moment of inertia of a circular disc about its diametral axis can be given as:
- Polar moment of inertia of a circular disc about its diametral axis can be given as:
- Mass moment of inertia of a sphere of radius R can be given as:
- Mass moment of inertia of a circular cone of radius R and height h about its axis of rotation can be given as:
- Mass moment of inertia of a hemisphere of radius R about axis perpendicular to its diametral plane can be given as:
- Mass moment of inertia of a hemisphere of radius R about an axis passing through its center in its diametral plane can be given as:
Answers
- c
- a
- a
- b
- c
- d
- d
- b
- c
- d
- b
- a
- a
- c
- a
Theory Questions
- What do you mean by centroid and center of gravity? What is the basic difference between centroid and center of gravity?
- Find the centroid of a rod of length L, and mass M, using the first principle.
- State the perpendicular and parallel axis theorem.
- Find the expression for the center of gravity for the hemisphere.
- Find the mass moment of inertia of hemisphere about a diametral axis.
- Find the moment of inertia of a triangle about the line parallel to its base and passing through the centroid.
- Find the moment of inertia of a disc:
- About a line perpendicular to the plane of the disc and passing through the centroid.
- About a line parallel to the plane of the disc and passing through the centroid.
- About a line perpendicular to the plane of the disc and passing through the perimeter.
- About a line of a tangent.
- Find the expression for mass moment of inertia of a sphere.
- Find the mass moment of inertia of a hollow cylinder about its axis passing through the centroid.
- Differentiate area moment of inertia from the mass moment of inertia.
Numerical Problems
- From a circular plate of diameter 100 mm, a circular part is cut out whose diameter is 50 mm as shown in Figure 11.25. Find the centroid of the remaining part.

FIGURE 11.25
- From a semi-circular lamina of radius r, a circular
lamina of radius r/2 is removed as shown in
Figure 11.26. Find the position of the centroid of
the remaining part.

FIGURE 11.26
- Compute the moment of inertia of the composite area as shown in Figure 11.27 about the axis xx.
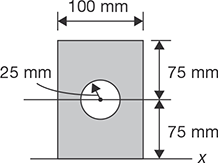
FIGURE 11.27
- Determine the moments of inertia and the radius of gyration of the section as shown in Figure 11.28 with respect to the x and y-axes.
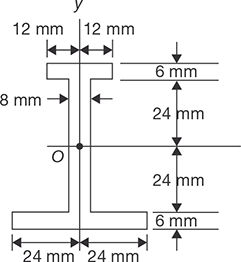
FIGURE 11.28
- Find the moment of inertia of the shaded section about the edge AB as shown in Figure 11.29.

FIGURE 11.29