CHAPTER 8

Isogenies, Connectedness, and Lie-Irreducibility

For each prime to P integer n, we have the n’th power homomorphism [n] : G → G. Formation of the direct image

M [n]_?M

is an exact functor from Perv to itself, which maps Neg to itself, P to itself, and which (because a homomorphism) is compatible with middle convolution:

[n]_?(M_?mid N) ≅ ([n]_?M) ?_mid ([n]_?N).

So for a given object N in P_arith, [n]_? allows us to view <N>_arith as a Tannakian subcategory of <[n]_?N>_arith, and <N>_geom as a Tannakian subcategory of <[n]_?N>_geom. For the fibre functor ! defined (after a choice of isomorphism G/k ≅ G_m/k) by

N !(N) := H⁰(A¹/k, j_0!N),

we have canonical functorial isomorphisms

!(N) = !([n]_?N).

So with respect to these fibre functors we have inclusions of Tannakian groups

G_{geom, [n]?N} ⊂ G_geom,N

and

G_arith,[n]?N ⊂ G_arith,N.

Theorem 8.1. Suppose that N in P_geom is semisimple and that n is a prime to p integer. Then G_geom,[n]?N is a normal subgroup of G_geom,N. The quotient group G_geom,N/G_geom,[n]?N is the cyclic group Z/dZ with

d := #{ζ ∈ μ_n(k)| δ_ζ ∈ <N>_geom},

and G_geom,[n]?N, seen inside G_geom,N, is the fixer of the objects

Proof. As N is semisimple, [n]_?N is also semisimple, hence G_geom,[n]?N is reductive. So G_geom,[n]?N is the fixer of its invariants in some representation of the ambient group G_geom,N, say corresponding to an object M in <N>_geom. Its invariants are the δ₁ subobjects of [n]_?M. These are precisely the subobjects [n]_?δ_ζ, ζ ∈ μ_n(k), of [n]_?M, i.e., the images by [n]_? of the subobjects δ_ζ, ζ ∈ μ_n(k), of M. Thus its space of invariants in M is the largest subobject of M which is punctual and supported in μ_n(k). So the space of G_geom,[n]?N -invariants is a G_geom,N stable subspace. Hence the fixer of these invariants, namely G_geom,[n]?N, is a normal subgroup of G_geom,N. A representation of the quotient is an object M in <N>_geom with [n]_?M geometrically trivial, i.e., a punctual object in <N>_geom which is supported in μ_n(k), i.e., a sum of the objects

{δ_ζ ∈ <N>_geom | ζ ∈ μ_n(k)}.

Thus we recover the reductive normal subgroup G_geom,[n]?N of G_geom,N as the fixer of these objects.

Recall that a representation ρ of an algebraic group G is said to be Lie-irreducible if it is both irreducible and remains irreducible when restricted to the identity component G⁰ of G.

Theorem 8.2. Suppose that N in P_arith is arithmetically semisimple and pure of weight zero (i.e., ι-pure of weight zero for every ι). Then N is geometrically Lie-irreducible (i.e., Lie-irreducible as a representation of G_geom,N) if and only if [n]_?N is geometrically irreducible for every integer n ≥ 1 prime to p. For n₀ the order of the finite group G_geom,N/G⁰_geom,N, we have

G⁰_geom,N = G_{geom, [n0]?N}.

Proof. If N is geometrically Lie-irreducible, then any subgroup of finite index in G_geom,N acts irreducibly. By the previous result, for each n ≥ 1 prime to p the group G_geom,[n]?N is of finite index, so acts irreducibly, i.e., [n]_?N is geometrically irreducible. Conversely, by Theorem 6.5, we know that G_geom,N/G⁰_{geom, N} is cyclic of some order n₀ prime to p. By Corollary 6.6, we know that G⁰_geom,N is the fixer of all punctual objects in <N>_geom. Moreover, by Theorem 6.5, the irreducible such punctual objects are precisely

{δ_ζ ∈ <N>_geom | ζ ∈ k^×} = {δ_ζ ∈ <N>_geom | ζ ∈ μ_n0(k)}.

Their fixer, by Theorem 8.1 above, is the subgroup G_geom,[n0]?N. Thus we have

G⁰_{geom, N} = G_geom,[n0]?N.

This second group acts irreducibly if (and only if) [n₀]_?M is geometrically irreducible.

Corollary 8.3. Suppose that N in P_arith is geometrically irreducible and pure of weight zero (i.e., ι-pure of weight zero for every ι). Then N is geometrically Lie-irreducible if and only if for every a = 1 ∈ k^× the multiplicative translate [x ax] N is not geometrically isomorphic to N.

Proof. Given two semisimple objects in P_geom, say A = M_in_iC_i and B = M_im_iC_i where the C_i are pairwise non-isomorphic, geometrically irreducible objects, and the integers n_i and m_i are ≥ 0, define the inner product

Thus a geometrically semisimple object N is geometrically irreducible if and only if <N, N>_geom = 1. Frobenius reciprocity gives, for each integer n prime to p,

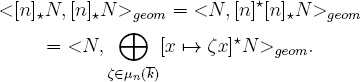
By the previous theorem, N is geometrically Lie-irreducible if and only if [n]_?N is geometrically irreducible for every integer n ≥ 1 prime to p, i.e., if and only if <[n]_?N, [n]_?N>_geom = 1 for every integer n ≥ 1 prime to p. By Frobenius reciprocity, this holds if and only if N is not geometrically isomorphic to any nontrivial multiplicative translate of itself by a root of unity of order prime to p. But every element of k^× is a root of unity of order prime to p.