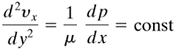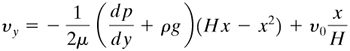EXAMPLE 3.8-1. Laminar Flow Between Horizontal Parallel Plates

Derive the equation giving the velocity distribution at steady state for laminar flow of a constant-density fluid with constant viscosity flowing between two flat and parallel plates. The velocity profile desired is at a point far from the inlet or outlet of the channel. The two plates will be considered to be fixed and of infinite width, with the flow driven by the pressure gradient in the x direction.

Solution: Assuming that the channel is horizontal, Fig. 3.8-1 shows the axes selected, with flow in the x direction and the width in the z direction. The velocities ν_y and ν_z are then zero. The plates are a distance 2y₀ apart.

The continuity equation (3.6-24) for constant density is

Equation 3.6-24

Since ν_y and ν_z are zero, Eq. (3.6-24) becomes

Equation 3.8-1

The Navier-Stokes equation for the x component is

Equation 3.7-36

Also, ∂ν_x/∂t = 0 for steady state, ν_y = 0, ν_z = 0, ∂ ν_x/∂x = 0, ∂²ν_x/∂x² = 0. We can see that ∂ν_x/∂z = 0, since there is no change of ν_x with z. Then ∂²ν_x/∂z² = 0. Making these substitutions into Eq. (3.7-36), we obtain

Equation 3.8-2

In fluid-flow problems we will be concerned with gravitational force only in the vertical direction for g_x, which is g, the gravitational force, in m/s². We shall combine the static pressure p and the gravitational force and call them simply p, as follows (note that g_x = 0 for the present case of a horizontal pipe but is not zero for the general case of a nonhorizontal pipe):

Equation 3.8-3

where h is the distance upward from any chosen reference plane (h is in the direction opposed to gravity). Then Eq. (3.8-2) becomes

Equation 3.8-4

We can see that p is not a function of z. Also, assuming that 2y₀ is small, p is not a function of y. (Some references avoid this problem and simply use p as a dynamic pressure, which is rigorously correct since dynamic pressure gradients cause flow. In a fluid at rest, the total pressure gradient is the hydrostatic pressure gradient, and the dynamic pressure gradient is zero.) Also, ∂p/∂x is a constant in this problem, since ν_x is not a function of x. Then Eq. (3.8-4) becomes an ordinary differential equation:

Equation 3.8-5

Integrating Eq. (3.8-5) once, using the condition dν_x/dy = 0 at y = 0 for symmetry,

Equation 3.8-6

Integrating again, using ν_x = 0 at y = y₀,

Equation 3.8-7

The maximum velocity in Eq. (3.8-7) occurs when y = 0, giving

Equation 3.8-8

Combining Eqs. (3.8-7) and (3.8-8),

Equation 3.8-9

Hence, a parabolic velocity profile is obtained. This result was also obtained in Eq. (2.9-9) when using a shell-momentum balance.

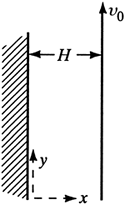
EXAMPLE 3.8-2. Laminar Flow Between Vertical Plates with One Plate Moving

A Newtonian fluid is confined between two parallel and vertical plates as shown in Fig. 3.8-2 (W6). The surface on the left is stationary and the other is moving vertically at a constant velocity ν₀. Assuming that the flow is laminar, solve for the velocity profile.

Solution: The equation to use is the Navier-Stokes equation for the y coordinate, Eq. (3.7-37):

Equation 3.7-37

At steady state, ∂ν_y/∂t = 0. The velocities ν_x and ν_z = 0. Also, ∂ν_y/∂y = 0 from the continuity equation, ∂ν_y/∂z = 0, and ρg_y = -ρg. The partial derivatives become derivatives and Eq. (3.7-37) becomes

Equation 3.8-10

This is similar to Eq. (3.8-2) in Example 3.8-1. The pressure gradient dp/dy is constant. Integrating Eq. (3.8-10) once yields

Equation 3.8-11

Integrating again gives

Equation 3.8-12

The boundary conditions are at x = 0, ν_y = 0 and at x = H, ν_y = ν₀. Solving for the constants, C₁ = ν₀/H - (H/2μ)(dp/dy + ρg) and C₂ = 0. Hence, Eq. (3.8-12) becomes

Equation 3.8-13

EXAMPLE 3.8-3. Laminar Flow in a Circular Tube

Derive the equation for steady-state viscous flow in a horizontal tube of radius r₀, where the fluid is far from the tube inlet. The fluid is incompressible and μ is a constant. The flow is driven in one direction by a constant-pressure gradient.

Solution: The fluid will be assumed to flow in the z direction in the tube, as shown in Fig. 3.8-3. The y direction is vertical and the x direction horizontal. Since ν_x and ν_y are zero, the continuity equation becomes ∂v_z/∂z = 0. For steady state ∂v_z/∂t = 0. Then substituting into Eq. (3.7-38) for the z component, we obtain

Equation 3.8-14

To solve Eq. (3.8-14), we can use cylindrical coordinates from Eq. (3.6-26), giving

Equation 3.6-26

Substituting these into Eq. (3.8-14),

Equation 3.8-15

The flow is symmetrical about the z axis, so ∂²ν_z/∂θ² is zero in Eq. (3.8-15). As before, dp/dz is a constant, and Eq. (3.8-15) becomes

Equation 3.8-16

Alternatively, Eq. (3.7-42) in cylindrical coordinates can be used for the z component and the terms that are zero discarded:

Equation 3.7-42

As before, ∂ν_z/∂t = 0, ∂²ν_z/∂θ² = 0, ν_r = 0, ∂v_z/∂θ = 0, ∂ν_z/∂z = 0. Then Eq. (3.7-42) becomes identical to Eq. (3.8-16).

The boundary conditions for the first integration are dν_z/dr = 0 at r = 0. For the second integration, ν_z = 0 at r = r₀ (tube radius). The result is

Equation 3.8-17

Converting to the maximum velocity as before,

Equation 3.8-18

If Eq. (3.8-17) is integrated over the pipe cross section using Eq. (2.9-10) to give the average velocity ν_{z av},

Equation 3.8-19

Integrating to obtain the pressure drop from z = 0 for p = p₁ to z = L for p = p₂, we obtain

Equation 3.8-20

where D = 2r₀. This is the Hagen-Poiseuille equation, derived previously as Eq. (2.9-11).

EXAMPLE 3.8-4. Laminar Flow in a Cylindrical Annulus

Derive the equation for steady-state laminar flow inside the annulus between two concentric horizontal pipes. This type of flow occurs often in concentric-pipe heat exchangers.

Solution: In this case Eq. (3.8-16) also still holds. However, the velocity in the annulus will reach a maximum at some radius r = r_max which is between r₁ and r₂, as shown in Fig. 3.8-4. For the first integration of Eq. (3.8-16), the boundary conditions are dν_z/dr = 0 at r = r_max, which gives

Equation 3.8-21

Also, for the second integration of Eq. (3.8-21), ν_z = 0 at the inner wall where r = r₁, giving

Equation 3.8-22

Repeating the second integration but for ν_z = 0 at the outer wall where r = r₂, we obtain

Equation 3.8-23

Combining Eqs. (3.8-22) and (3.8-23) and solving for r_max,

Equation 3.8-24

In Fig. 3.8-4 the velocity profile predicted by Eq. (3.8-23) is plotted. For the case where r₁ = 0, r_max in Eq. (3.8-24) becomes zero and Eq. (3.8-23) reduces to Eq. (3.8-17) for a single circular pipe.

EXAMPLE 3.8-5. Velocity Distribution for Flow Between Coaxial Cylinders

Tangential laminar flow of a Newtonian fluid with constant density is occurring between two vertical coaxial cylinders in which the outer one is rotating (S4) with an angular velocity of ω, as shown in Fig. 3.8-5. It can be assumed that end effects can be neglected. Determine the velocity and the shear-stress distributions for this flow.

Solution: On physical grounds the fluid moves in a circular motion; the velocity ν_r in the radial direction is zero and ν_z in the axial direction is zero. Also, ∂ρ/∂t = 0 at steady state. There is no pressure gradient in the θ direction. The equation of continuity in cylindrical coordinates as derived before is

Equation 3.6-27

All terms in this equation are zero.

The equations of motion in cylindrical coordinates, Eqs. (3.7-40), (3.7-41), and (3.7-42), reduce to the following, respectively:

Equation 3.8-25

Equation 3.8-26

Equation 3.8-27

Integrating Eq. (3.8-26),

Equation 3.8-28

To solve for the integration constants C₁ and C₂, the following boundary conditions are used: at r = R₁, ν_θ = 0; at r = R₂, ν_θ = ωR₂. The final equation is

Equation 3.8-29

Using the shear-stress component for Newtonian fluids in cylindrical coordinates,

Equation 3.7-31

The last term in Eq. (3.7-31) is zero. Substituting Eq. (3.8-29) into (3.7-31) and differentiating gives

Equation 3.8-30

The torque T that is necessary to rotate the outer cylinder is the product of the force times the lever arm:

Equation 3.8-31

where H is the length of the cylinder. This type of device has been used to measure fluid viscosities from observations of angular velocities and torque and has also been used as a model for some friction bearings.

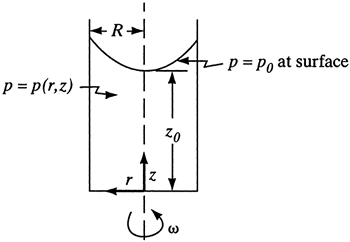
EXAMPLE 3.8-6. Rotating Liquid in a Cylindrical Container

A Newtonian fluid of constant density is in a vertical cylinder of radius R (Fig. 3.8-6) with the cylinder rotating about its axis at angular velocity ω (B2). Find the shape of the free surface at steady state.

Solution: The system can be described in cylindrical coordinates. As in Example 3.8-5, at steady state, ν_r = ν_z = 0 and g_r = g_θ = 0. The final equations in cylindrical coordinates given below are the same as Eqs. (3.8-25)-(3.8-27) for Example 3.8-5, except that g_z = -g in Eq. (3.8-27):

Equation 3.8-32

Equation 3.8-33

Equation 3.8-34

Integration of Eq. (3.8-33) gives the same equation as in Example 3.8-5:

Equation 3.8-28

The constant C₂ must be zero since ν_θ cannot be infinite at r = 0. At r = R, the velocity ν_θ = Rω. Hence, C₁ = ω and we obtain

Equation 3.8-35

Combining Eqs. (3.8-35) and (3.8-32),

Equation 3.8-36

Hence, we see that Eqs. (3.8-36) and (3.8-34) show that pressure depends upon r because of the centrifugal force and upon z because of the gravitational force:

Equation 3.8-34

Since the term p is a function of position, we can write the total differential of pressure as

Equation 3.8-37

Combining Eqs. (3.8-34) and (3.8-36) with (3.8-37) and integrating,

Equation 3.8-38

The constant of integration can be determined, since p = p₀ at r = 0 and z = z₀. The equation becomes

Equation 3.8-39

The free surface consists of all points on this surface at p = p₀. Hence,

Equation 3.8-40

This shows that the free surface is in the shape of a parabola.