8.4. Nonlinear predictions and retransformation of random components

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

8.4. Nonlinear predictions and retransformation of random components

Given a variety of approximation methods in the analysis of nonlinear longitudinal data, the fixed effects and the covariance parameters in GLMMs can be derived either from the linearization approaches or from the integral approximation methods. In displaying results of various nonlinear longitudinal models, it is often not sufficient to produce meaningful interpretations just by presenting parameter estimates and the corresponding standard errors. For example, in the presence of more than two nominal response outcomes, the regression coefficients of covariates do not necessarily bear any relationship to changes in the multinomial response (Greene, 2003; Liao, 1994; Liu et al., 1995). Because a set of probabilities for competing outcomes always sum up to unity, the simultaneous structural variation in the probability distribution of more than two alternatives is indeed beyond what a set of regression coefficients can capture. Therefore, in the application of GLMMs, the researcher often needs to compute nonlinear predictions on repeated measurements of the response, given selected values of the covariates, the estimated regression coefficients, and the random effect approximates.

In this section, I describe three approaches for performing nonlinear predictions in the application of GLMMs: the best linear unbiased prediction, or BLUP (Kuk, 1995; McGilchrist, 1994), the empirical Bayes estimate (SAS, 2012, Chapter 64), and the retransformation method (Liu and Engel, 2012; McCulloch et al., 2008).

8.4.1. Best linear unbiased prediction based on linearization

The BLUP applied in the analysis of nonlinear longitudinal data is the extension of the BLUP approximation in linear mixed models (described in Chapter 4). These predicting approaches essentially modify the EM algorithm on the conditional expectation of the random effects, with the data replaced by the predictors based on the mode of the corresponding conditional distribution.

The BLUP procedure in GLMMs is often based on linearized normal data of the nonlinear response with

\tilde{y}

$\tilde{y}$

replacing y. Given Equation (8.39)

$V (\tilde{θ}) = ZG Z' + {\tilde{∆}}^{- 1} A^{1 / 2} R (\tilde{α}) A^{1 / 2} {\tilde{∆}}^{- 1},$ $V (\tilde{θ}) = ZG Z' + {\tilde{∆}}^{- 1} A^{1 / 2} R (\tilde{α}) A^{1 / 2} {\tilde{∆}}^{- 1},$

the random error

\tilde{ɛ}

$\tilde{ɛ}$

, conditionally on b, is assumed to be normally distributed. The maximum log pseudo likelihood for

\tilde{y}

$\tilde{y}$

can then be written as

$l (\tilde{θ}, y) = \frac{1}{2} \log |V (\tilde{θ})| - \frac{1}{2} {(\tilde{y} - X' β)}^{'} V {(\tilde{θ})}^{- 1} (\tilde{y} - X' β) - \frac{\tilde{N}}{2} \log (2 π),$ $l (\tilde{θ}, y) = \frac{1}{2} \log |V (\tilde{θ})| - \frac{1}{2} {(\tilde{y} - X' β)}^{'} V {(\tilde{θ})}^{- 1} (\tilde{y} - X' β) - \frac{\tilde{N}}{2} \log (2 π),$

(8.61)

where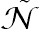

\tilde{N}

$\tilde{N}$

is the sum of frequencies used in the analysis.

Likewise, the corresponding restricted log pseudo-likelihood function is

$\begin{array}{l} l_{R} (\tilde{θ}, y) = \frac{1}{2} \log |V (\tilde{θ})| - \frac{1}{2} {(\tilde{y} - X' β)}^{'} V {(\tilde{θ})}^{- 1} (\tilde{y} - X' β) \\ - \frac{1}{2} \log |X' V {(\tilde{θ})}^{- 1} X| - \frac{\tilde{N} - \tilde{M}}{2} \log (2 π), \end{array}$ $\begin{array}{l} l_{R} (\tilde{θ}, y) = \frac{1}{2} \log |V (\tilde{θ})| - \frac{1}{2} {(\tilde{y} - X' β)}^{'} V {(\tilde{θ})}^{- 1} (\tilde{y} - X' β) \\ - \frac{1}{2} \log |X' V {(\tilde{θ})}^{- 1} X| - \frac{\tilde{N} - \tilde{M}}{2} \log (2 π), \end{array}$

(8.62)

where

\tilde{M}

$\tilde{M}$

is the rank of X (if X has full rank,

\tilde{M} = M

$\tilde{M} = M$

According to the standard estimating procedure for linear mixed models, the researcher can estimate the fixed parameters and predict the random effects by using the following two equations, respectively:

$\hat{β} = {[X^{'} V {(\hat{\tilde{θ}})}^{- 1} X]}^{- 1} X^{'} V {(\hat{\tilde{θ}})}^{- 1} \tilde{y},$ $\hat{β} = {[X^{'} V {(\hat{\tilde{θ}})}^{- 1} X]}^{- 1} X^{'} V {(\hat{\tilde{θ}})}^{- 1} \tilde{y},$

(8.63)

$\hat{b} = \hat{G} Z^{'} V {(\hat{\tilde{θ}})}^{- 1} (\tilde{y} - X^{'} \hat{β}) .$ $\hat{b} = \hat{G} Z^{'} V {(\hat{\tilde{θ}})}^{- 1} (\tilde{y} - X^{'} \hat{β}) .$

(8.64)

Equations (8.63) and (8.64) display the similarities of the BLUP used for the linearized pseudo data and the BLUP described in Chapter 4. The predictor

\hat{b}

$\hat{b}$

in Equation (8.64) is the estimated BLUP in linearization models. The final predictor can be obtained by iterations given a standard procedure of convergence. The above two equations are based on the condition that

φ = 1

$φ = 1$

; if the scale parameter

φ \neq 1

$φ \neq 1$

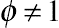, the equations can be easily adjusted by applying some standard approaches (for details, see SAS, 2012, Chapter 38).

According to the rationale of the BLUP estimator for nonlinear predictions, the procedure yields the best and unbiased predictors on the transformed linear function. By retransforming a transformed linear function to predict the nonlinear response variable, the predicted outcomes are regarded to be unbiased. Given the specification of the pseudo-error term

\tilde{ɛ}

$\tilde{ɛ}$

in the linearization models, however, nonlinear predictions of the response must include retransformation of this error term in the retransformation process. If the link function for a GLMM is not identity, normality of the transformed random errors in the linearization model needs to be retransformed to a nonnormal distribution as a prior when the nonlinear response is predicted. As a result, the expected value of the posterior predictive distribution, after retransformation to a nonnormal function, is not the direct retransformation of the expectation in the linear predictor unless the identity link function is specified.

Given the complex functional transformation and retransformation, in nonlinear predictions the above BLUPs are neither linear nor best; further computation is needed to derive the nonlinear, the unbiased, and the statistically best predictions. As Kuk (1995) comments, in general situations, the BLUP estimates are asymptotically biased and inconsistent in nonlinear predictions. In some of the empirical illustrations in the succeeding chapters, the prediction bias from neglect of retransforming the random components in nonlinear predictions will be described and empirically displayed.

8.4.2. Empirical Bayes BLUP

As the random effects can be estimated or predicted accurately by the application of the Gaussian quadrature methods (McCulloch et al., 2008), the nonlinear response for subject i in GLMMs can be predicted by using the estimates of the fixed effects and the predicted values of the specified random effects. Given Equation (8.17), the linear predictor for subject i can be expressed by the mean

${\hat{η}}_{i} (y_{i} |\hat{β}, {\hat{b}}_{i}) = X_{i}^{'} \hat{β} + Z_{i}^{'} {\hat{b}}_{i},$ ${\hat{η}}_{i} (y_{i} |\hat{β}, {\hat{b}}_{i}) = X_{i}^{'} \hat{β} + Z_{i}^{'} {\hat{b}}_{i},$

(8.65)

where

\hat{β}

$\hat{β}$

is the maximum or the REML estimate of

β

$β$

, and

{\hat{b}}_{i}

${\hat{b}}_{i}$

is the empirical Bayes estimate of b_i. The corresponding variance of the prediction is given by

${\hat{V}}_{i} ({\hat{η}}_{i}) = \hat{φ} {\hat{A}}_{i}^{1 / 2} (μ_{i}) {\hat{R}}_{i} (\tilde{a}) {\hat{A}}_{i}^{1 / 2} (μ_{i}) + Z_{i}^{'} \hat{G} Z .$ ${\hat{V}}_{i} ({\hat{η}}_{i}) = \hat{φ} {\hat{A}}_{i}^{1 / 2} (μ_{i}) {\hat{R}}_{i} (\tilde{a}) {\hat{A}}_{i}^{1 / 2} (μ_{i}) + Z_{i}^{'} \hat{G} Z .$

(8.66)

Suppose

{\hat{η}}_{i}

${\hat{η}}_{i}$

is a random vector of linear predictors from Equation (8.65) with mean

η_{i}

$η_{i}$

and variance matrix

{\hat{V}}_{i} ({\hat{η}}_{i})

${\hat{V}}_{i} ({\hat{η}}_{i})$

, and

{\hat{y}}_{i} = g^{- 1} ({\hat{η}}_{i})

${\hat{y}}_{i} = g^{- 1} ({\hat{η}}_{i})$

is a transform of

{\hat{η}}_{i}

${\hat{η}}_{i}$

where g is the link function and g⁻¹ is its inverse function. The first-order Taylor series expansion of

g^{- 1} ({\hat{η}}_{i})

$g^{- 1} ({\hat{η}}_{i})$

yields an approximation of mean

$E [g^{- 1} ({\hat{η}}_{i})] \approx g^{- 1} (η_{i}),$ $E [g^{- 1} ({\hat{η}}_{i})] \approx g^{- 1} (η_{i}),$

(8.67)

and the variance–covariance matrix

{\hat{V}}_{i} ({\hat{η}}_{i})

${\hat{V}}_{i} ({\hat{η}}_{i})$

$V_{i} [g^{- 1} ({\hat{η}}_{i})] \approx {[\frac{\partial g^{- 1} ({\hat{η}}_{i})}{\partial {\hat{η}}_{i}} |{\hat{η}}_{i} = η_{i}]}^{'} V_{i} ({\hat{η}}_{i}) [\frac{\partial g^{- 1} ({\hat{η}}_{i})}{\partial {\hat{η}}_{i}} |{\hat{η}}_{i} = η_{i}] .$ $V_{i} [g^{- 1} ({\hat{η}}_{i})] \approx {[\frac{\partial g^{- 1} ({\hat{η}}_{i})}{\partial {\hat{η}}_{i}} |{\hat{η}}_{i} = η_{i}]}^{'} V_{i} ({\hat{η}}_{i}) [\frac{\partial g^{- 1} ({\hat{η}}_{i})}{\partial {\hat{η}}_{i}} |{\hat{η}}_{i} = η_{i}] .$

(8.68)

The above approximation approach uses the delta method (Stuart and Ord, 1994), described in Appendix B. Computation of the partial derivatives expressed in Equation (8.68) depends on a specific link function corresponding to a specific data type, as will be described in some of the succeeding chapters.

This empirical Bayes BLUP is a popular approach for performing nonlinear predictions with GLMMs (Fitzmaurice et al., 2004), applied in a variety of computer software packages without various algorithms. For example, the SAS NLMIXED procedure uses the likelihood calculation given in McGilchrist (1994), with an extension of the algorithm for nonlinear predictions. Specifically, this statistical procedure uses the empirical Bayes estimates of the random effects to approximate the Gaussian quadrature integral, and the approximated integral as a marginal likelihood is then used and optimized by iteration for the fixed effects. In the final iteration, the PROC NLMIXED procedure applies the fixed effect estimates to produce final predictions, considered the empirical Bayes estimates (for details, see the Chapter “The NLMIXED Procedure” in the SAS/STAT User’s Guide). In this algorithm, only the predicted random effects, used as the fixed effects, are taken into account in predictions, thereby implicitly leading to the restriction that the intraindividual correlation is one. As indicated in Chapter 4, the term

G Z^{'} Σ^{- 1}

$G Z^{'} Σ^{- 1}$

in linear mixed models is empirically the proportion of the overall variance–covariance matrix that derives from the random effects. Given this inference, there should actually be two variance–covariance components, R and G, which need to be accounted for in nonlinear predictions with GLMMs.

8.4.3. Retransformation method

According to Equation (8.15), the mean of the nonlinear response y can be formulated as an iterated expectation:

$E (y_{i}) = E [g^{- 1} (X_{i}^{'} β + Z_{i}^{'} b)] .$ $E (y_{i}) = E [g^{- 1} (X_{i}^{'} β + Z_{i}^{'} b)] .$

(8.69)

If g(·) represents a log link, Equation (8.69) can be rewritten as

$\begin{array}{l} E (y_{i}) = E [\exp (X_{i}^{'} β + Z_{i}^{'} b)] \\ = \exp (X_{i}^{'} β) E [\exp (Z_{i}^{'} b)] \\ = \exp (X_{i}^{'} β) Φ_{b} (Z_{i}), \end{array}$ $\begin{array}{l} E (y_{i}) = E [\exp (X_{i}^{'} β + Z_{i}^{'} b)] \\ = \exp (X_{i}^{'} β) E [\exp (Z_{i}^{'} b)] \\ = \exp (X_{i}^{'} β) Φ_{b} (Z_{i}), \end{array}$

(8.70)

where

Φ_{b} (Z_{i})

$Φ_{b} (Z_{i})$

is defined as the moment-generating function of b evaluated at Z_i (McCulloch et al., 2008). According to Bayesian inference,

Φ_{b} (Z_{i})

$Φ_{b} (Z_{i})$

is the expectation of the prior distribution for the random effects on the nonnormal y_i. Given

b_{i} \sim N (0, G)

$b_{i} \sim N (0, G)$

, this moment-generating function of b follows a lognormal distribution with the log link. Therefore, Equation (8.70) can be further expanded for nonlinear predictions:

$E ({\hat{y}}_{i}) = \exp (X_{i}^{'} \hat{β}) \exp (\frac{Z_{i} \hat{G} Z_{i}^{'}}{2}),$ $E ({\hat{y}}_{i}) = \exp (X_{i}^{'} \hat{β}) \exp (\frac{Z_{i} \hat{G} Z_{i}^{'}}{2}),$

(8.71)

where the term

\exp \{(Z_{i j} \hat{G} Z_{i j}^{'}) / 2\}

$\exp \{(Z_{i j} \hat{G} Z_{i j}^{'}) / 2\}$

is the expectation of

\exp (Z_{i}^{'} b)

$\exp (Z_{i}^{'} b)$

given a lognormal distribution.

Equation (8.71) indicates that at data point j,

\exp (X_{i j}^{'} \hat{β}) \exp \{(Z_{i j} \hat{G} Z_{i j}^{'}) / 2\} > \exp (X_{i j}^{'} \hat{β})

$\exp (X_{i j}^{'} \hat{β}) \exp \{(Z_{i j} \hat{G} Z_{i j}^{'}) / 2\} > \exp (X_{i j}^{'} \hat{β})$

unless all elements in

\hat{G}

$\hat{G}$

take value zero. Therefore, given the log link, nonlinear response y_ij will be underpredicted if retransformation of the between-subjects random effects is completely or partially neglected, with the magnitude of such retransformation bias depending on the value of the elements in

\hat{G}

$\hat{G}$

. Furthermore, it is inappropriate to replace

\hat{G}

$\hat{G}$

with the empirical BLUP covariance estimator

var (BLUP {\hat{b}}_{i})

$var (BLUP {\hat{b}}_{i})$

. Due to shrinkage of

{\hat{b}}_{i}

${\hat{b}}_{i}$

toward the population fixed effects, the distribution of the empirical BLUPs does not accurately represent the distribution of the random effects (McCulloch and Neuhaus, 2011).

Equation (8.69) does not specify a term for within-subject random errors. The underlying rationale is that the specification of the between-subjects random effects fundamentally reflects the individual differences in unspecified characteristics thereby, addressing within-subject variability (Diggle et al., 2002; Littell et al., 2006; Molenberghs and Verbeke, 2010). Neither the linearization-based BLUP nor the empirical-Bayes method specifies within-subject random errors in nonlinear predictions. While empirically this hypothesis holds in most cases, Equation (8.69) does not universally reflect the true experiences generated by the stochastic longitudinal processes. There is evidence that within-subject variability can sometimes have a unique impact on the nonlinear response, thereby yielding some uncertainty, even conditionally on the between-subjects random effects (Liu and Engel, 2012). In certain situations, a term for within-subject random errors needs to be specified in line with the specification in linear mixed models.

If within-subject variability is considered, the specification of nonlinear response y for person i can be empirically written as

$E (y_{i}) = E \{g^{- 1} [X_{i}^{'} β + Z_{i}^{'} b + \tilde{∆} (y_{i} - μ_{i})]\},$ $E (y_{i}) = E \{g^{- 1} [X_{i}^{'} β + Z_{i}^{'} b + \tilde{∆} (y_{i} - μ_{i})]\},$

(8.72)

where

\tilde{∆}

$\tilde{∆}$

can be regarded as a second-order smearing estimate evaluated at

(\hat{β}, {\hat{b}}_{i})

$(\hat{β}, {\hat{b}}_{i})$

. This smearing effect can be approximated from the partial derivative of the log-likelihood function with respect to β in GLMMs, given by

$\hat{\tilde{∆}} (y_{ij} - μ_{ij}) \approx \frac{\partial l (y_{i j} |β, G, φ)}{\partial β} |_{\hat{β}, \hat{b}} .$ $\hat{\tilde{∆}} (y_{ij} - μ_{ij}) \approx \frac{\partial l (y_{i j} |β, G, φ)}{\partial β} |_{\hat{β}, \hat{b}} .$

Empirically,

\tilde{∆}

$\tilde{∆}$

is the local approximation of within-subject random errors (McCulloch et al., 2008), which can be estimated as the first partial derivative of the log-likelihood function. It must be emphasized that the approximation of such a within-subject random error term is model-based, differing from the specification of random errors in linear mixed models. If the researcher has strong evidence that between-subjects variability well captures within-subject uncertainty, the specification of the above local approximation step is unnecessary.

Some researchers recommend the application of the latent variable approach (Amemiya, 1985; Bock, 1975; Long, 1997) to estimate within-subject random errors in GLMMs (Hedeker and Gibbons, 2006). In the analysis of multinomial data, this random component on each logit function is assumed to follow a standard logistic distribution with mean 0 and variance π²/3. This standardized approach specifies a constant variance of within-subject random errors, regardless of the response type and the number of covariates considered in a particular regression model. It is argued that, when the between-subjects random effects are specified, not that much variability remains in a binary or a multinomial response (Littell et al., 2006). Furthermore, this approach does not specify a covariance structure between two related logit components, thereby overlooking the multivariate nature of the multinomial response. Indeed, the assumption of a continuous latent distribution is just a rough model requirement (McCullagh and Nelder, 1989).

Empirically, within-subject random errors can be locally approximated by the score equation, the first partial derivative of the log-likelihood in estimating a marginal mean function. If all covariates are rescaled to be centered at some specified values, represented by X₀, the intercept corresponds to a mean transformed linear function with respect to X₀, as applied in the regression analysis of correlated binary data (Zhao and Prentice, 1990) and for predicting the mean function of recurrent events in survival analysis (Lin et al., 2000). For example, if time T is centered at three and other covariates are rescaled to be centered at sample means, the intercept in a GLMM predicts the mean of the transformed linear function for an average person at the time point valued 3. Correspondingly, the score function approximates the within-subject residuals for this marginal mean conditionally on the between-subjects random effects and other model parameters. The variances–covariance elements of within-subject random errors can also be approximated by the local subset of the variance–covariance matrix for the fixed effects given the hypothesized structure of R.

If within-subject random errors are considered in GLMMs, for a log link the mean of the nonnormal response y is given by

$\begin{array}{l} E (y_{i}) = E [\exp (X_{i}^{'} β + Z_{i}^{'} b + {\tilde{∆}}_{i}^{- 1})] \\ = \exp (X_{i}^{'} β) Φ_{b} (Z_{i}) \exp [E ({\tilde{∆}}_{i}^{- 1})] \\ = \exp (X_{i}^{'} β) \exp (\frac{Z_{i} G Z_{i}^{'} + A_{i}}{2}), \end{array}$ $\begin{array}{l} E (y_{i}) = E [\exp (X_{i}^{'} β + Z_{i}^{'} b + {\tilde{∆}}_{i}^{- 1})] \\ = \exp (X_{i}^{'} β) Φ_{b} (Z_{i}) \exp [E ({\tilde{∆}}_{i}^{- 1})] \\ = \exp (X_{i}^{'} β) \exp (\frac{Z_{i} G Z_{i}^{'} + A_{i}}{2}), \end{array}$

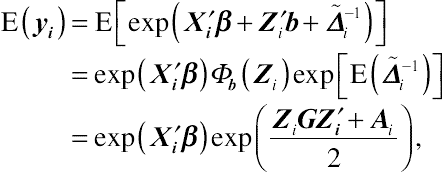(8.73)

with variance generally specified as

$\begin{array}{l} var (y_{i}) = var [E (y_{i} |b)] + E [var (y_{i} |b)] \\ = var (μ_{i}) + E [φ υ (μ_{i})] \\ = var [g^{- 1} (X_{i}^{'} β + Z_{i}^{'} b)] + E \{φ υ [g^{- 1} (X_{i}^{'} β + Z_{i}^{'} b)]\} . \end{array}$ $\begin{array}{l} var (y_{i}) = var [E (y_{i} |b)] + E [var (y_{i} |b)] \\ = var (μ_{i}) + E [φ υ (μ_{i})] \\ = var [g^{- 1} (X_{i}^{'} β + Z_{i}^{'} b)] + E \{φ υ [g^{- 1} (X_{i}^{'} β + Z_{i}^{'} b)]\} . \end{array}$

(8.74)

As can be identified, the variance of response y can be decomposed into two parts: the between-subjects and the within-subject components, as in the case of linear mixed models. In such nonlinear predictions, the value of the unobservable and the unrecognized factors is set at the mean by using the expectation of the posterior predictive distribution for the retransformed random effects, just as researchers have often set values of the control variables at sample means in regression modeling. When two variance components are specified, the marginal distribution of a nonlinear function is overdispersed compared to the conditional distribution (McCulloch et al., 2008).

The development of the retransformation method follows the rationale of Bayesian inference by predicting the marginal mean of the nonlinear response with the assumed distribution of an unknown parameter. This predictor is actually a nonlinear adaptation to least squares means applied for linear mixed models, accounting for the expectation of a nonnormal posterior predictive distribution for the random components. Dispersion of the individual development is configured by the standard error of the margin. In this approach, the random effects are specified to account for the inherent intraindividual correlation in longitudinal data, but the random effect values are not of direct interest. Therefore, in nonlinear predictions, the value of the random effects is held at its mean, just as values of the observed control variables are routinely fixed at sample means. In statistical modeling, individuals are the elements in a sample randomly selected for the estimation of population statistics, and therefore, any specific person in the sample just happens to be chosen from the population. With inference from a random sample to the population it represents, a prediction for a specific individual should follow a nonnormal probability distribution if the link function is not identity.

8.5. Some popular specific generalized linear mixed models

The nonlinear distribution of a nonnormal response variable often follows some distinctive patterns. Such recognizable characteristics have enabled statisticians and other quantitative methodologists to apply a variety of GLMMs for analyzing nonlinear longitudinal data of different types. Empirically, several specific GLMMs have been widely applied to describe certain data types. For example, in the analysis of binary longitudinal data, a logistic or a probit regression mixed model can be used to incorporate and estimate both the fixed and the random effects. Likewise, if the response variable takes more than two levels but they are ordered, the ordered logistic or probit regression with the random effects may be employed; when a discrete response variable is neither dichotomous nor ordered, the mixed-effects multinomial logit model is the appropriate perspective for predicting longitudinal trajectories of the probabilities.

In this section, a number of popular families of nonnormal distributions are introduced, with a brief description of specifications for each data type. These approaches include the logistic, the ordered logistic or probit, the multinomial logit, the Poison models, and the survival analysis. These specific GLMMs have been applied frequently in the analysis of nonlinear longitudinal data, and the concrete specifications and inferences for two of these families will be delineated extensively in Chapters 10 and 11, respectively.

8.5.1. Mixed-effects logistic regression model

The mixed-effects logistic regression model is commonly used to analyze the binary longitudinal data. Let y_ij be the value of the observed dichotomous response variable, coded 0 or 1, associated with time point j nested within subject i. The mixed-effects logistic regression model is generally expressed in terms of the log odds of the probability for a specific response, denoted P_ij. This specific link function is referred to as the logit link, given by

$\log (\frac{P_{i j}}{1 - P_{i j}}) = X_{i j}^{'} β + Z_{ij} b .$ $\log (\frac{P_{i j}}{1 - P_{i j}}) = X_{i j}^{'} β + Z_{ij} b .$

(8.75)

If within-subject variability is specified to account for uncertainty at a specific time point, Equation (8.75) needs to be modified by adding a term of within-subject random errors. As evaluated at X_ij and b, the within-subject random term can be viewed as a second-order expansion evaluated at

(\hat{β}, {\hat{b}}_{i})

$(\hat{β}, {\hat{b}}_{i})$

, given by

$\log (\frac{P_{i j}}{1 - P_{i j}}) = X_{i j}^{'} β + Z_{i j}^{'} b + \tilde{∆} (y_{i} - μ_{i}) .$ $\log (\frac{P_{i j}}{1 - P_{i j}}) = X_{i j}^{'} β + Z_{i j}^{'} b + \tilde{∆} (y_{i} - μ_{i}) .$

(8.76)

Retransformation of the above logit regression with mixed effects gives rise to the following mixed-effects nonlinear model, with the probability of a positive response (y_ij = 1) as the dependent:

$\begin{array}{l} P_{i j} (y_{ij} = 1 |b_{i}, X_{i j}, Z_{ij}) = g^{- 1} [X_{i j}^{'} β + Z_{ij} b + \tilde{∆} (y_{i} - μ_{i})] \\ = \frac{\exp [X_{i j}^{'} β + Z_{ij} b + \tilde{∆} (y_{i} - μ_{i})]}{1 + \exp [X_{i j}^{'} β + Z_{ij} b + \tilde{∆} (y_{i} - μ_{i})]} . \end{array}$ $\begin{array}{l} P_{i j} (y_{ij} = 1 |b_{i}, X_{i j}, Z_{ij}) = g^{- 1} [X_{i j}^{'} β + Z_{ij} b + \tilde{∆} (y_{i} - μ_{i})] \\ = \frac{\exp [X_{i j}^{'} β + Z_{ij} b + \tilde{∆} (y_{i} - μ_{i})]}{1 + \exp [X_{i j}^{'} β + Z_{ij} b + \tilde{∆} (y_{i} - μ_{i})]} . \end{array}$

(8.77)

Clearly, in the mixed-effects logistic regression model, the inverse link function is the logistic cumulative distribution function (c.d.f.). Given the statistical property in the logistic regression that the probability density function (p.d.f.) is related to the c.d.f. in a simple way, the mixed-effects logistic regression model is preferable for analyzing the binary longitudinal response data. For its importance in longitudinal data analysis, Chapter 10 is devoted entirely to the description of this popular perspective, including general specifications, statistical inferences, nonlinear predictions, and an empirical illustration.

The mixed-effects probit model, which is based on the standard normal distribution, is occasionally used as an alternative approach in the analysis of binary longitudinal data. In this regression model, the normal c.d.f. and p.d.f. replace those of the logistic distributions. Analytic results generated from the probit model, however, are not as easy to interpret as those from the logistic regression. Given the striking similarities between the logistic and the probit distributions, in this book the mixed-effects probit model on the binary data is not further elaborated.

8.5.2. Mixed-effects ordered logistic model

The mixed-effects ordered logistic and probit regression modes are the extensions of the mixed-effects binary logistic and probit models, with the qualitative response variable taking more than two values with the multiple levels being ordered. In health research, a prominent example is health status measured by the discrete levels of disability severity. The following specifications are focused on the ordered logistic perspective given its analytic simplicity and popularity.

The specification of the mixed-effects ordered logistic model is based on the assumption that there exists a latent variable underlying the discrete and ordered response, denoted by y^*, which is continuously distributed and follows a logistic distribution. Since y^* is unobservable, an ordinal variable y is specified as the discrete realization of the continuous variable y^*. Let K + 1 denote the ordered response levels with k = 1, 2, …, K + 1. The mixed-effects ordered logistic model uses K cumulative category comparisons, and accordingly, K cumulative logit functions are defined. The conditional cumulative probabilities for the K + 1 categories of the outcome y_ij are written as

${\tilde{P}}_{i j k} = prob (y_{i j} \leq k |b_{i}, X_{i j}) = \sum_{l = 1}^{k} P_{i j l},$ ${\tilde{P}}_{i j k} = prob (y_{i j} \leq k |b_{i}, X_{i j}) = \sum_{l = 1}^{k} P_{i j l},$

where

P_{i j l}

$P_{i j l}$

represents the conditional probability of response in level l (l = 1, 2, …, K + 1), and

{\tilde{P}}_{i j k}

${\tilde{P}}_{i j k}$

is the conditional cumulative probability of responses from level 1 to k. The mixed-effects cumulative logit model for the conditional cumulative probabilities is given in terms of the cumulative logits, written as

$\log (\frac{{\tilde{P}}_{i j k}}{1 - {\tilde{P}}_{i j k}}) = γ_{k} - (X_{i j}^{'} β + Z_{i j}^{'} b_{i}), k = 1,..., K,$ $\log (\frac{{\tilde{P}}_{i j k}}{1 - {\tilde{P}}_{i j k}}) = γ_{k} - (X_{i j}^{'} β + Z_{i j}^{'} b_{i}), k = 1,..., K,$

(8.78)

where γ_k is a series of increasing model thresholds (γ₁ < γ₂ < … < γ_K). These thresholds permit the cumulative response probabilities to differ. For identification, either the first threshold γ₁ or the model intercept β₀ needs to be set at zero. Notice that in Equation (8.78), the regression coefficients in β do not carry subscript k, and therefore, the mixed-effects ordered logistic regression model assumes the effects of covariates to be constant across all logit components. This hypothesis of the identical odds ratios across the K cutoffs is called the proportional odds assumption (McCullagh, 1980).

The conditional probability of a response in level k can be obtained from the difference in two conditional cumulative probabilities. Let the inverse link function, denoted by

Ψ (η_{i j k})

$Ψ (η_{i j k})$

, be the logistic cumulative distribution function (c.d.f.). Then, the conditional probability of a response in level k is given by

$P (y_{i j} = k |b_{i}, X_{i j}, Z_{ij}) = Ψ (η_{i j k}) - Ψ (η_{i j k - 1}) .$ $P (y_{i j} = k |b_{i}, X_{i j}, Z_{ij}) = Ψ (η_{i j k}) - Ψ (η_{i j k - 1}) .$

(8.79)

Given the constraint that a set of probabilities must sum up to unity, changes in various probabilities can be negatively correlated. Consequently, the assumption of constant regression coefficients or odds ratios across all K response levels is not realistic in empirical analyses. Perhaps due to this reason, the mixed-effects multinomial logit model, briefly introduced in the next section, is a much more popular perspective than the ordered approach in the analysis of longitudinal data with more than two discrete levels. Therefore, the mixed-effects cumulative logit model is not further described in this text. The reader interested in the mixed-effects ordered regression models is referred to Hedeker and Gibbons (1994, 2006, Chapter 10).

8.5.3. Mixed-effects multinomial logit regression models

The mixed-effects multinomial logit regression model is routinely applied when the multiple discrete levels of the response variable are not ordered, or the proportional odds assumption cannot be satisfied for ordered data. In longitudinal data analysis, the probability that y_ij = k (response falls in level k) for subject i at time point j, conditionally on the random effects b, is given by

$\begin{array}{l} P_{i j k} = \Pr (y_{i j} = k |b_{i}, X_{i j}, Z_{i j}) \\ = {[1 + \sum_{l = 1}^{K} \exp (X_{i j}^{'} β_{l} + Z_{i j}^{'} b_{i l})]}^{- 1} \exp (X_{i j}^{'} β_{k} + Z_{i j}^{'} b_{i k}), for k = 1,2, ..., K, \end{array}$ $\begin{array}{l} P_{i j k} = \Pr (y_{i j} = k |b_{i}, X_{i j}, Z_{i j}) \\ = {[1 + \sum_{l = 1}^{K} \exp (X_{i j}^{'} β_{l} + Z_{i j}^{'} b_{i l})]}^{- 1} \exp (X_{i j}^{'} β_{k} + Z_{i j}^{'} b_{i k}), for k = 1,2, ..., K, \end{array}$

(8.80)

and

$\begin{array}{l} P_{i j (K + 1)} = \Pr (y_{i j} = K + 1 |b_{i}, X_{i j}, Z_{i j}) \\ = {[1 + \sum_{l = 1}^{K} \exp (X_{i j}^{'} β_{l} + Z_{i j}^{'} b_{i l})]}^{- 1} . \end{array}$ $\begin{array}{l} P_{i j (K + 1)} = \Pr (y_{i j} = K + 1 |b_{i}, X_{i j}, Z_{i j}) \\ = {[1 + \sum_{l = 1}^{K} \exp (X_{i j}^{'} β_{l} + Z_{i j}^{'} b_{i l})]}^{- 1} . \end{array}$

(8.81)

In the above two equations of the mixed-effects multinomial logit model, both the regression coefficients β_k and the random effects carry subscript k, thereby assuming that the regression coefficients and the variance–covariance matrix of the random effects vary across response levels. In this model, the fixed-effects parameters represent differences relative to the last level, namely K + 1, used as the reference. Given the importance of this model in longitudinal data analysis, Chapter 11 is entirely devoted to the mixed-effects multinomial logit regression model.

8.5.4. Mixed-effects Poisson regression models

The mixed-effects Poisson regression model is proposed for analyzing the discrete frequency of a response variable, the so-called count data. Let y_ij be the value of a count variable (y_ij = 0, 1, …) for subject i at time point j, and the count is assumed to be drawn from a Poisson distribution. The mixed-effects Poisson regression model then specifies the expected number of counts, given by

$\log (μ_{i j}) = X_{i j}^{'} β + Z_{i j}^{'} b_{i} .$ $\log (μ_{i j}) = X_{i j}^{'} β + Z_{i j}^{'} b_{i} .$

(8.82)

In the longitudinal setting, the time variable is usually specified in the mixed-effects Poisson regression model, termed T_ij. Given this addition, Equation (8.82) can be rewritten as

$\log (μ_{i j}) = \log T_{i j} + X_{i j}^{'} β + Z_{i j}^{'} b_{i},$ $\log (μ_{i j}) = \log T_{i j} + X_{i j}^{'} β + Z_{i j}^{'} b_{i},$

(8.83)

where the term log T_ij is called an offset. Taking antilog values on both sides of Equation (8.83) yields the expected number of count, given by

$μ_{i j} = T_{i j} \exp (X_{i j}^{'} β + Z_{i j}^{'} b_{i}) .$ $μ_{i j} = T_{i j} \exp (X_{i j}^{'} β + Z_{i j}^{'} b_{i}) .$

(8.84)

Given the Poisson process for the count y_ij, the probability that y_ij = y, conditionally on the random effects b, is

$P (y_{i j} = y |b_{i}, X_{i j}, Z_{ij}) = \exp (- μ_{i j}) \frac{{(μ_{i j})}^{y}}{y!} .$ $P (y_{i j} = y |b_{i}, X_{i j}, Z_{ij}) = \exp (- μ_{i j}) \frac{{(μ_{i j})}^{y}}{y!} .$

(8.85)

In many longitudinal datasets, count data exhibit more zero counts than what is consistent with the Poisson distribution. In such situations, the zero-inflated Poisson (ZIP) mixed model may be applied to handle statistical instability from such data inflation (Land et al., 1996; Nagin and Land, 1993). A logistic or a probit regression model, which predicts the probability of a nonzero response, is combined with a Poisson regression for the zero and nonzero counts to derive more efficient parameter estimates and more reliable nonlinear predictions.

For practical purposes, it is sometimes convenient to define the univariate random effects as gamma distributed in the application of the mixed-effects Poisson regression model on longitudinal count data (McCulloch et al., 2008). In empirical analyses, however, adding multiple normally distributed random effects of the Poisson regression model can provide a more general and flexible perspective.

Notice that the Poisson distribution has the basic property

var (μ_{i j}) = μ_{i j}

$var (μ_{i j}) = μ_{i j}$

. This restriction somewhat limits the applicability of the mixed-effects Poisson regression model in longitudinal data analysis. In many occasions, counts can be conveniently viewed as a discrete realization of a continuous normal distribution as long as it takes a sufficient number of values. Therefore, linear mixed models can sometimes serve as an alternative approach for analyzing longitudinal count data. The desirable large-sample property generally results in statistically efficient, consistent, and robust parameter estimates.

Given its limited applicability in longitudinal data analysis, the mixed-effects Poisson regression model is not further delineated in the remainder of this text. The interested reader is referred to Hedeker and Gibbons (2006, Chapter 12), Land et al. (1996), and McCulloch et al. (2008).

8.5.5. Survival models

Survival models are used to analyze sequential occurrences of events governed by probabilistic laws. In survival analysis, a popular and predominant approach is to model the hazard rate in which covariates are specified to impact on the hazard function. In those regression models, each observation under investigation is assumed to be subject to an instantaneous hazard rate, h(T), of experiencing a particular event, where T = 0, 1, ..., ∞. Because the hazard rate is always nonnegative, the effects of covariates are generally specified as a multiplicative term exp(X′β), as in the case of many other exponential distribution perspectives. Specifically, the hazard rate model on the causal relationships between covariates and lifetime processes is written as

$h (T |X) = h_{0} (T) exp (X' β),$ $h (T |X) = h_{0} (T) exp (X' β),$

(8.86)

where h₀(T) denotes a specified or an unspecified baseline hazard function for continuous survival time

\overset{⌣}{T}

$\overset{⌣}{T}$

, and β provides a set of the effects of covariates on the hazard rate, with the same length as X. As can be seen from Equation (8.86), the effects of X on the hazard rate are multiplicative, or proportional, so that the predicted value of h(T) given X, denoted by h′(T|X), can be restricted in the range [0, ∞]. Nonmultiplicativity of the effects of given covariates, if it exists, can be captured by the specification of one or more interaction terms, contained in X. Given the specifications, this class of nonlinear regression models is referred to as the proportional hazard rate model. In this survival model, all individuals are assumed to follow a common univariate hazard function, with individual heterogeneity primarily reflected in the proportional scale change for a stratification of distinct population subgroups.

If the term h₀(T) in Equation (8.86) represents a parametric baseline hazard function attached to a particular probability distribution of survival time

\overset{⌣}{T}

$\overset{⌣}{T}$

, the hazard rate model is called the parametric hazard regression model, with parameters estimated by the ML method. For example, if the observed hazard function varies monotonically over time, the Weibull regression model may be specified:

$h (T, X; \overset{⌣}{T} \sim W e i l) = \tilde{λ} \tilde{p} {(λ T)}^{\tilde{p} - 1} \exp (X' β),$ $h (T, X; \overset{⌣}{T} \sim W e i l) = \tilde{λ} \tilde{p} {(λ T)}^{\tilde{p} - 1} \exp (X' β),$

(8.87)

where the symbols

\tilde{λ}

$\tilde{λ}$

and

\tilde{p}

$\tilde{p}$

are the scale and the shape parameters in the Weibull function, respectively. Equation (8.87) is the Weibull regression mode with the baseline Weibull distributional function multiplied by the scale exp(X′β).

If the term h₀(T) in Equation (8.86) represents an arbitrary and unspecified baseline hazard function for continuous survival time

\overset{⌣}{T}

$\overset{⌣}{T}$

, the model is called the Cox proportional hazard rate model, often simply referred to as the Cox model (Cox, 1972). Technically, the Cox model uses the ML algorithm to fit a partial likelihood function, with the estimating approach referred to as partial likelihood. Because of its simplicity, robustness, and efficiency, the Cox model becomes a very popular approach for analyzing the effects of covariates on the dynamic process of experiencing a particular event over time. Given the proportional hazards assumption, the application of this model has almost covered all applied disciplines, ranging from clinical trials to criminological research, the analysis of social networks, and health services utilization. The development of various refined methods, such as time-dependent covariates and the stratified proportional hazard model, further widens the applicability of the Cox model, particularly in situations where the proportionality assumption in the Cox model is violated.

In statistics, survival analysis is considered to be an independent area of statistical modeling. Although some scientists include survival models as a part of longitudinal data analysis (Singer and Willett, 2003), survival analysis is more conventionally regarded as a unique domain of statistical analysis that is parallel with longitudinal data analysis. Therefore, the detailed methods and techniques of survival analysis will not be further described in the remainder of this text. For a thorough reading of survival analysis, the interested reader is referred to Andersen et al. (1993), Kalbfleisch and Prentice (2002), Lawless (2003), and Liu (2012).

8.6. Summary

In this chapter, I describe GLMMs in the context of longitudinal data analysis. Some specific methods for estimating GLMMs are delineated extensively. Given the importance of nonlinear predictions on the discrete response outcomes, a number of popular techniques in this regard are introduced and compared. All these methods are based on specific assumptions and hypotheses on parameters, often found to yield significantly different analytic results. In nonlinear predictions of nonnormal longitudinal outcomes, the practice of the Bayesian inference plays a very important role in deriving unbiased marginal means. The specification of the random effects is essential to yield correct analytic results in GLMMs but they are often of no direct interest to researchers; therefore, in nonlinear predictions, the researcher usually only needs to account for the expectation of the posterior predictive distribution for the random effects.

When estimating a nonlinear mixed model, a number of approximation methods are described in this chapter, with each possessing its own strengths and limitations. The so-called linearization-based approaches, such as PQL and MQL, are flexible for modeling data with complex structures, but they are fitted on pseudo data from linearization of nonlinear functions, thereby potentially yielding biased parameter estimates and model fit statistics. Integral approximation techniques, such as the Laplace and adaptive Gaussian quadrature, are based on the log-likelihood of observed data, therefore providing more reliable model fit statistics than the linearization methods. Those integral approximation methods, however, do not have sufficient capacity to accommodate complex covariance structures, and consequently, they can be applied effectively only when the number of the random effects is restricted. Furthermore, the reliability of the random effect estimates relies heavily on the quality of starting values in the application of the integral approximation methods.

Given the strengths and limitations attached to each of these approximation methods, I would like to recommend the use of a hybrid scheme in which a linearization algorithm is used first to obtain starting values for the application of the more refined but more restrictive integral approximation approaches. For example, the adaptive Gaussian quadrature approximation to the log-likelihood function probably gives the best mix of efficiency and accuracy (Pinheiro and Bates, 1995), but it is sensitive to the quality of starting values in the estimation of the random effects. As a result, the researcher might want to use the PQL or the MQL method first to derive an initial set of parameter estimates, and then borrow those estimates as the starting values in the application of the Gaussian quadrature approximation. In some of the succeeding chapters, the application of this hybrid approach will be displayed with empirical illustrations.

When the specified random effects are associated with complex covariance structures, the application of the accurate Gaussian quadrature methods becomes computationally tedious, and instead, the Laplace approximation may be used as an alternative. In contrast to the quadrature approaches, the MCMC approximation is less accurate but is more practicable for handling more complex covariance structures.

In this chapter, a number of popular families of mixed-effects nonlinear regression models are described. Choosing an appropriate GLMM should be based on the data type, the specification of a corresponding link function, the distribution of the response variable, and the correlation structure of the dependent variable. Prior knowledge and profound learning on a topic of research can help the researcher make correct decisions. Misspecification of these four factors can have important consequences. For example, specifying a normal distribution when the outcome data are counts can sometimes lead to incorrect statistical conclusions.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 8.4. Nonlinear predictions and retransformation of random components

Create new playlist

Sign In

Sign Up

8.4. Nonlinear predictions and retransformation of random components

8.4.1. Best linear unbiased prediction based on linearization

8.4.2. Empirical Bayes BLUP

8.4.3. Retransformation method

8.5. Some popular specific generalized linear mixed models

8.5.1. Mixed-effects logistic regression model

8.5.2. Mixed-effects ordered logistic model

8.5.3. Mixed-effects multinomial logit regression models

8.5.4. Mixed-effects Poisson regression models

8.5.5. Survival models

8.6. Summary

Table of Contents for
8.4. Nonlinear predictions and retransformation of random components