So far, a large number of statistical models have been described on normal, continuous longitudinal outcome data. In many occasions, a response variable in the longitudinal setting is discrete, and the application of linear mixed models is no longer valid. When the distribution of the response variable is not normal (or not multivariate normal) or the variance/covariance matrices are not homogeneous longitudinally, the use of linear mixed models can lead to serious estimating errors and result in unrealistic predicted values of the response. Statisticians and other quantitative methodologists have developed a variety of statistical models to analyze such nonnormal longitudinal data by combining the standard nonlinear regression and the mixed modeling techniques. There are different types of nonnormal longitudinal data, such as binary, ordinal, count, and multinomial. In this text, I refer to these data types as nonlinear longitudinal data with a fairly narrow definition. While for each data type there are corresponding specifications and estimating procedures, the underlying expressions and statistical inferences in many of those models can be generalized by a unifying perspective, with much of such unification following the tradition of generalized linear models (GLMs).
In this chapter, I first provide a brief overview on the basic specifications of GLMs, based on which the general inference of generalized linear mixed models (GLMMs) is introduced given the incorporation of random effects. Next, a variety of statistical methods are delineated for the estimation of the fixed and the random effects in GLMMs, which is followed by the description of the standard approaches for nonlinear predictions and the retransformation method. To help the reader better comprehend the applicability of these methods, I also provide a brief summary on a number of specific GLMMs dealing with different types of discrete longitudinal data. The detailed specifications and inferences of some of these models, given their importance in longitudinal data analysis, will be further described in the succeeding chapters. In
Section 8.6, the merits and remaining issues are summarized with respect to GLMMs.
8.1. A brief overview of generalized linear models
GLMs are a statistical perspective unifying a variety of statistical models that relate the response variable to linear combinations of covariates through a link function (
McCullagh and Nelder, 1989;
Nelder and Wedderburn, 1972). As many types of response variables and error structures can be taken as special cases in such a generalization, GLMs consist of a large number of distributional functions, such as linear, binomial, Poisson, gamma, negative binomial, and multinomial. These different distributional functions can be expressed by a unique family of probability distributions in statistics – the exponential distribution family, also referred to as the log linear distribution family. With the tremendous flexibility to combine so many models into a unified algorithm, GLMs can be used to model rates and proportions, binary, ordinal, multinomial variables, and counts as well as the continuous outcome data as a special case. Remember that the term GLMs here refers to generalized linear models, not general linear models.
GLMs are based on the assumption that the underlying type of the response is generated from a particular distribution included in the exponential family. Let the vector y with length N be a realization of a random variable Y whose components are independently distributed with mean μ. Let g(y) be a function related to a specific exponential family of distributions of y as associated linearly with a covariate matrix X. Then, the mean or the expectation of the inverse of the distribution, namely μ, relies on the independent covariates X, written as
E(y)=μ=g−1(X′β),
 (8.1)
(8.1)where E(y) is the expected value of y. Correspondingly, the variance of y is a function of the mean, given by
var(y)=var[g−1(X′β)].
 (8.2)
(8.2)In GLMs, such dependence of variance on the mean is referred to as the variance function. Therefore, in GLMs, y can follow a probability distribution other than normality.
Given the aforementioned properties, a typical GLM is considered to consist of the following three elements, as summarized by
McCullagh and Nelder (1989):
1. a probability distribution from the exponential family,
2. a systematic component represented by the linear predictor
X′β
, and
3. a link function g such that
E(y)=μ=g−1(η),
where η is the mean of the linear predictor, a transformed normal response variable.
In terms of the probability distribution in GLMs, the p.d.f. of any distribution in the exponential family can be expressed in the form
f(yi|θi,φ)=exp[yiθi−⌢a(θi)φ+˜b(yi;φ)],
 (8.3)
(8.3)where
θ is a parameter related to the mean of the distribution, generally referred to as the natural or canonical parameter given certain conditions, and in the exponential distribution family it is generally given by
θi=X′iβ
. The parameter
φ is associated with the variance of the distribution called the dispersion or a scale parameter. When
φ is known, Equation
(8.3) represents a single-parameter exponential family distribution; when
φ is unknown, on the other hand, it becomes a two-parameter distributional function. The functions
⌢a(⋅)
and
˜b(⋅)
indicate a specific member in the exponential family, such as normal, binomial, counts, or multinomial. As the prediction of
y involves only the fixed linear predictor, GLMs are actually the statistical expressions for the marginal mean
g−1(X′β)
, with the variance function evaluated at the predicted marginal mean
g−1(X′ˆβ)
.
By the above specification, the exponential family unifies many probability distributions of the response. After a series of statistical inferences, the following properties about the mean and the variance of y in GLMs are identified:
E(yi)=μi=∂⌢a(θi)∂θ,
 (8.4)
(8.4)var(yi)=φ∂2⌢a(θi)∂θ2.
 (8.5)
(8.5)The reader interested in the derivation of Equations
(8.4) and
(8.5) is referred to McCullagh and Nelder (1989, pp. 28–29). By definition, a specific distribution in the exponential family reflects a special form of stochastic processes in the response.
The systematic component, or the linear predictor, reflects the information about the effects of the model covariates on the mean of the distribution of y via the link function. Let η be the mean of the transformed linear combinations of unknown parameters β. Then η can be expressed in the linear form
η=X′β.
 (8.6)
(8.6)Here, the concept linear in the specification of GLMs points more to a statistical expression than to a substantive link. With specification of a polynomial function in an independent variable, for example, the relationship between the mean response and a covariate is no longer linear. Nevertheless, such nonlinearity can be well accommodated in the exponential distribution family by appropriate transformation of the covariate.
The link function indicates the relationship between the linear predictor and the mean of the underlying distributional function. In the standard linear regression, the mean and the linear predictor are identical, referred to as the identity link. With the availability of many commonly used link functions, the arbitrary selection of an appropriate distributional function should depend on the nature of the response variable and the value range of nonlinear predictions. For example, if the response variable is dichotomous, the probability of the occurrence of a selected response is regularly modeled. Given the binary data, the logistic or probit regression model can be applied to satisfy the condition that the predicted probability must fall in the range between 0 and 1. Likewise, if the response consists of more than two nominal levels, the multinomial logistic regression is widely used to predict the probability for each level, with model covariates linearly related to a set of log odds. For such link functions, the mean of the response is transformed to its nonlinear function η, thereby conveniently generating the unrestricted range from minus infinity to plus infinity in the transformed linear predictor. Given such flexibility, hypothesis testing associated with GLMs does not require normality or multivariate normality of the response variable and homogeneity of variances.
In some GLMs, the regression coefficient of a covariate does not necessarily reflect the true relationship between that covariate and the mean of the underlying distribution function, particularly since the linear predictor is related to a transform rather than to the mean (
Fox, 1987). A prominent example in this regard is the difficulty in interpreting the regression coefficients estimated for multinomial logistic models (
Greene, 2003). In such circumstances, additional computation is required to aid in the interpretation of analytic results, as will be discussed in some of the succeeding chapters.
With respect to the estimation of parameters in GLMs, the maximum likelihood (ML) is the most popular estimator, although some other algorithms, such as the empirical Bayes method and the least squares, also see substantial applications. Let
yi follow a specific probability distribution in the exponential distribution family with parameter
θi. From the expression specified in Equation
(8.3), the joint probability over
N such probability functions can then be specified, given by
L=∏Ni=1Li(θi) =∏Ni=1exp[yiθi−⌢a(θi)φ+˜b(yi;φ)].
 (8.7)
(8.7)Taking log values on both sides of Equation
(8.7), a log-likelihood function is
l=∑Ni=1[yiθi−⌢a(θi)φ+˜b(yi;φ)].
 (8.8)
(8.8)Clearly, in the construct of GLMs, the log-likelihood function is computationally simpler than the likelihood function itself, just as the case of linear regression modeling. Therefore, the log-likelihood function is generally specified in statistical inference for GLMs.
There are standard procedures to maximize a log-likelihood function with respect to the parameter vector θ for generating robust, efficient, and consistent parameter estimates. Specifically, the process starts with the construction of a score statistic vector, denoted by Ũi(θ) for subject i and mathematically defined as the first partial derivatives of the log-likelihood function with respect to θ. The total score equation with N observations from a likelihood function is
˜U(θ)=∂∂ θl(θ|y)=∑Ni=1∂∂θli(θ).
 (8.9)
(8.9)The minus second derivatives of the log-likelihood function, or the minus Hessian of the log-likelihood, yields the estimator of variances and covariances for Ũ(θ), given by
˜V(θ)=−(E∂2l(θ|y)∂θ∂θ′).
 (8.10)
(8.10)Statistically,
Ũ(
θ) is asymptotically normal, given the large-sample approximation to the joint distribution of parameters, with mean
0 and variance–covariance matrix
˜V(θ)
. Therefore, the parameter vector
θ can be efficiently estimated by solving the equation
˜U(θ)=∂∂θl(θ|y)=0.
 (8.11)
(8.11)The above procedure is the formalization of a typical maximum likelihood estimator (MLE) in GLMs. The vectors of MLE parameter estimates are generally referred to as
ˆθ
. For a large sample,
ˆθ
is the unique solution of
Ũ(
θ) =
0, so that
ˆθ
is consistent
for
θ and
√N(ˆθ−θ)
is asymptotically multivariate normal as
N → ∞. Therefore,
ˆθ
can be written by
ˆθ∼N[0,˜V(θ)−1].
 (8.12)
(8.12)This MLE is based on the observed Fisher information matrix, denoted by
I(ˆθ)
, given by
I(ˆθ)=−(∂2l(ˆθ)∂ˆθ∂ˆθ′).
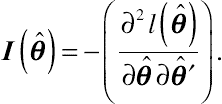 (8.13)
(8.13)As can be easily recognized,
˜V(θ)
, formulated in Equation
(8.10), contains the expected values of
I(ˆθ)
. The inverse of the observed information matrix yields the estimator of the variance–covariance matrix for parameter estimates. For a GLM only containing natural parameters, the variance–covariance matrix for the estimates of
β can be written by
Σ(ˆβ)=I(ˆβ)−1.
 (8.14)
(8.14)Operationally, the ML estimates are generally not available in the closed form, and the estimation of β is regularly performed through an iterative weighted algorithm, using either a Newton–Raphson or a Fisher’s scoring method. The specific MLEs and the model fit statistics in several GLMs will be described briefly in some of the successive chapters.
The construction of GLMs is based on the assumption that in the presence of model covariates, observations are independent of each other. Such an assumption does not usually apply to longitudinal data in which subject-specific observations are correlated, even in the presence of covariates. Broadly, there are two classes of refined modeling techniques to handle dependence in longitudinal data: the generalized estimating equations (GEEs) and GLMMs. While
Chapter 9 of this book is entirely devoted to GEEs, in the
Section 8.2 some basic specifications and inferences on the latter approach are provided.
8.2. Generalized linear mixed models and statistical inferences
As indicated previously, the independence hypothesis in GLMs does not usually hold in the longitudinal setting because repeated measurements are nested within subjects, thereby being correlated, even in the presence of model parameters. Statistically, the random effects can be specified in a GLM to account for intraindividual correlation inherent in nonlinear longitudinal data. By this addition, the fixed-effects nonlinear regression is combined with one or more terms of the random effects, thereby resulting in a special form of GLMs with mixed effects. Such statistical models are
referred to as GLMMs. While linear mixed models can be taken as a special case of GLMMs, there have been substantial methodological developments for the analysis of nonlinear longitudinal data (
Breslow and Clayton, 1993;
Breslow and Lin, 1995;
Diggle et al., 2002;
Molenberghs and Verbeke, 2010; Pinheiro and Bates, 1995; Stiratelli et al., 1984;
Zeger and Karim, 1991 and many others).
In this section, I describe the basic specifications and statistical inferences of GLMMs and the associated likelihood functions in the presence of random effects.
8.2.1. Basic specifications of generalized linear mixed models
Technically, GLMMs are a straightforward extension of the classical generalized linear perspective from univariate data to clustered measurements. Let
yi={yi1,...,yini}′
be a realization of a random variable
Yi with mean
μi and variance–covariance
Vi. Suppose that g(
yi,
Xi) is a nonlinear function linking
yi to the covariate vector
Xi={Xi1,...,Xini}′
and a
q × 1 vector of unknown individual random effects
bi={bi1,...,biq}′
. In the construct of GLMMs, the function g(
yi,
Xi,
bi) is assumed to be associated linearly with
Xi and
bi where g is a link function. The mean of the response variable for subject
i at
ni time points, namely
μi, is then a modification of Equation
(8.1) given the addition of the random effect vector
bi, written as
E(yi)=μi=E[g−1(X′iβ+Z′ibi)],
 (8.15)
(8.15)where E(
yi) is a set of expected values of the conditional distribution of the response given the random effects. With this specification, GLMMs are also referred to as the conditional model in contrast to the marginal GEE, which will be described in
Chapter 9. Analogous to the specification in GLMs,
β is the
M × 1 vector of unknown regression parameters to be estimated. The term
Zi is a design matrix, and
bi represents the between-subjects random effects assumed to be distributed as
N(0,G)
. As in linear mixed models,
Zi often contains time or one or more other covariates whose association with the response is assumed to vary between subjects. Given these specifications, the components of
Yi are assumed to be independent of each other conditionally on covariate
Xi and the random effect vector
bi.
In the exponential distribution family, random errors for many specific functions depend on the mean function, and therefore, the specification of the variance in GLMMs is complex. In the longitudinal setting, within-subject random errors are generally specified as embedded in a distributional function, and consequently, Equation
(8.15) implicitly involves two random components. Generally, the variance function of
yi in GLMMs can be written as
var(yi)=var(μi)+E[φυ(μi)]=var[g−1(X′β+Z′ibi)]+E{φυ[g−1(X′β+Z′ibi)]},
 (8.16)
(8.16)where
ν is a specific variance function, and
φ represents a scale factor for overdispersion. Given this flexible specification,
yi can be specified as following a probability distribution other than multivariate normality. In Equation
(8.16), the expression of the variance in
yi given
bi is determined by the structure of a specific GLMM, and thus, the
R matrix in nonlinear longitudinal data cannot be specified freely as in linear mixed modeling (McCulloch et al., 2008). This property in GLMMs will be further discussed in the succeeding texts.
The corresponding linear predictor of GLMMs can be written as
ηi[E(yi|bi)]=X′iβ+Z′ibi.
 (8.17)
(8.17)Equation
(8.17) does not specify a within-subject error term given the complexity of the variance function. Indeed, without making assumptions about g(·) and the conditional distribution of
yi, the distribution of within-subject random errors and its variance cannot be specified in a direct, explicit fashion. Even so, for analytic convenience of expressing uncertainty in GLMMs, some researchers prefer to express the above linear predictor by including an error term, given by
ηi[E(yi|bi)]=X′iβ+Z′ibi+ɛi,
 (8.18)
(8.18)where
ɛi={ɛi1,...,ɛini}′
is the vector of within-subject random errors representing uncertainty in the response. The vector of within-subject random errors
ɛi, conditionally on
bi, is often assumed to have the property
E(ɛi|bi)=0
. The specification of such random errors, however, is much more complex than in linear mixed models, with variances and covariances depending on a specific link function belonging to the exponential distribution family.
Let
˜α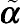
be a correlation parameter, and
R(˜a)
be the
ni ×
ni matrix of
˜α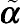
describing the correlation pattern within subject
i. In situations where both intraindividual correlation and heterogeneity of within-subject error variance are evident, the common within-subject variance–covariance structure can be expressed as
var(ɛi|bi)=φA1/2i(μi)Ri(˜a)A1/2i(μi),
 (8.19)
(8.19)where
Ai(μi)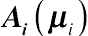
is an
ni ×
ni diagonal within-subject variance matrix containing elements
ν, evaluated at
μi in the formulation of a specific GLMM, and
Ri is unknown.
For analytic simplicity without loss of generality, the matrices included in Equation
(8.19) are often assumed to be common to all subjects. Compared to the variance–covariance matrix specified for linear mixed models that depends on
i through its dimension, Equation
(8.19) allows dependence on
i through the subject-specific information and the individual response, given
β
and
bi. Such generalization provides a flexible structure for accommodating complex patterns of within-subject variability associated with nonlinear longitudinal data. In empirical studies, the
convenient and commonly used assumption of normality is often made about the conditional distribution of
ɛi given
β and
bi, given by
ɛi|β,bi=N{0,φA1/2i(μi)Ri(˜a)A1/2i(μi)}.
 (8.20)
(8.20)The vector of the between-subjects random effects bi is generally assumed to follow a multivariate normal distribution with vector 0 and q × q variance–covariance matrix G, analogous to the specification for linear mixed models. Given the inclusion of bi, one or more elements in β are assumed to vary across subjects, either randomly or related to a systematic effect. The structure of G depends on the researcher’s hypothesis on the mechanisms inherent in unobserved heterogeneity for a target population. If the elements of bi are assumed to be uncorrelated, G needs to be specified as a diagonal matrix.
Given the above specifications, the variance–covariance matrix for GLMMs is formally given by
Vi=φA1/2i(μi)Ri(˜a)A1/2i(μi)+Z′iGZ.
 (8.21)
(8.21)As can be summarized from the above presentations, GLMMs permit the accommodation of nonnormal responses by means of a nonlinear link function between the mean of the response and the predictors. Furthermore, they can model overdispersion and intraindividual correlation by including the random effects (
McCulloch, 1997). In some of the succeeding chapters, I will formulate some specific functional forms and various variance–covariance structures associated with GLMMs with specific link functions. For more details concerning the general specifications of nonlinear mixed models, the interested reader is referred to
Davidian and Giltinan (1995),
Lindstrom and Bates (1990), and McCulloch et al. (2008).
8.2.2. Statistical inference and likelihood functions
As indicated in
Chapter 3, statistical inference of regression models is meant to specify likelihood functions for the estimation of model parameters. In the construct of GLMMs, the unique aspect of statistical inference is the way to predict the random effects in addition to the estimation of the fixed regression parameters. For analytic convenience, the random effects in the linear predictor are usually assumed to be randomly, normally distributed with zero expectation. The normality hypothesis on the random effects in GLMMs is usually valid because the range of the parameter space for the mean can be transformed into the complete interval between −∞ and ∞ (McCulloch et al., 2008).
Let
yi be an
ni-dimensional vector of repeated measurements of the response for subject
i and
bi∼N(0,G)
be the
q-dimensional vector of the random effects. By extending the probability distribution of GLMs to the GLMM context, the p.d.f. of any distribution in GLMMs can then be expressed as
f(yij|β,bi,φ)=exp[yijθij−⌢a(θij)φ+˜b(yij;φ)],
 (8.22)
(8.22)where
yij is the response measure for subject
i at time point
j, and
θij is the parameter related to the mean of the distribution. In the longitudinal setting,
θij can be specified by vector
θi=ηi=X′iβ+Z′ib
. The functions
⌢a(⋅)
and
˜b(⋅)
as well as the scale factor
φ are the same as defined earlier, and the inverse of the mean vector for a known link function is specified by Equation
(8.18).
With the specification of the p.d.f., GLMMs can be fitted by maximizing the likelihood by integrating out the random effects. With Equation
(8.22), the likelihood contribution of subject
i is
fi(yi|β,G,φ)=∫∏nij=1fij(yij|β,bi,φ)f(bi|G)dbi,
 (8.23)
(8.23)where the integration is over the q-dimensional distribution of bi. The joint likelihood function over N subjects is given by
L(β,G,φ)=∏Ni=1fi(yi|β,G,φ) =∏Ni=1∫∏nij=1fij(yij|β,bi,φ)f(bi|G)dbi.
 (8.24)
(8.24)The log-likelihood function of GLMMs can be formulated by taking log values of both sides of Equation
(8.24):
logL(β,G,φ)=log[∏Ni=1∫∏nij=1fij(yij|β,bi,φ)f(bi|G)dbi] =∑i,j[yijθij−⌢a(θij)φ+b(yij;φ)]+∑ilog∫∞−∞f(bi|G)db.
 (8.25)
(8.25)The second term in the second equality of Equation
(8.25) is not easy to estimate empirically. There are a variety of methods for approximating this log-likelihood function, as will be described in
Section 8.3. The analytic results from different approximating methods, however, are often found to differ markedly.
The fact that the GLMMs’ formalization is conditional on the unobservable random effects sometimes calls for the application of the Bayes methodology to derive the model fit. In this approach, prior distributions are specified for
β,
φ, and
G, usually assuming prior independence, with the corresponding densities written as
f(β)
,
f (
φ
), and
f (
G), respectively. There are different ways to select prior distributions, and most recommendations and preferences for the selection are based on the empirical data evidence given a specific link function of the response.
With the specification of the priors, the posterior distribution can be written as
f(β,G,φ,b1,...,bN|Y1,...,YN)∝∏Ni=1∏nij=1fi(yij|β,bi,φ)∏Ni=1f(bi|G)f(G)f(β)f(φ).
 (8.26)
(8.26)For analytic convenience without loss of generality, the fixed effect β, the random effect bi, the variance components in G, and φ are generally specified as taking simple forms in GLMMs, and correspondingly, the standard algorithms can be applied to draw samples from the posterior distribution. The specification of complex variance–covariance structures for the random effects often results in serious numeric problems.
With the complexity of data structures in GLMMs, the Bayes approach is usually applied to estimate the between-subject random effects
bi, the fixed effects
β, and the variance components
φ and
G within an integrated process. In this process, the estimator
ˆbi
is the value of
bi that maximizes the density
fi(bi|yi,β,G,φ)
, where the unknown parameters are replaced by the estimates from the ML estimation. The resulting estimates are the empirical Bayes estimates. In the application of GLMMs, nonlinear predictions of the response outcomes are often required to aid in the interpretation of analytic results, and in such predictions, the random effect approximates are included to predict both the conditional and the marginal longitudinal trajectory of individuals.
There are some advantages with the application of the Bayes approach. First, it avoids the need for numerical integration by taking repeated samples from the posterior distributions with the use of complex techniques. Second, the Bayes method is flexible to assess uncertainty in the estimated random effects and the functions of model parameters. In the meantime, the Bayes approach is associated with several weaknesses in the analysis of nonnormal longitudinal data. While the Bayes approach for GLMMs is flexible, the posterior distribution is often skewed, thereby making the underlying normality hypothesis questionable (
Molenberghs and Verbeke, 2010).
8.2.3. Procedures of maximization and hypothesis testing on fixed effects
In GLMMs, maximizing the log-likelihood function with respect to
β and
bi, as specified in Equation
(8.25), yields the MLE of the parameters. The general procedure is to estimate the fixed and the random effects,
β and
bi, separately. Because the second term of the second equality in Equation
(8.25) does not include
β, the first partial derivative of the log-likelihood function with respect to
β can be written as
∂∂βl(β,G,φ)=∂∂β∫f(y|b)f(b|G)db/f(y) =∫[∂∂βf(y|b)]f(b|G)db/f(y) =∫[∂∂βlogf(y|b)]f(b|y)db.
 (8.27)
(8.27)A similar derivation can be formulated for the ML equations in terms of the random-effects parameters given the distribution of f (b). The first partial derivative of the log-likelihood function with respect to b is
∂∂bl(β,G,φ)=∫∂logf(β)∂bf(b|y)db =E[∫∂logf(β)∂b|y].
 (8.28)
(8.28)In the empirical application, there are considerable challenges to formalizing the above equations given nonlinearity of the response. Because no analytic expressions are available for the integrals in Equation
(8.25), numerical approximations or some other statistical procedures are required to specify close forms of the log-likelihood function for the estimation of parameters. There are several popular approaches of such approximations in the literature of nonlinear longitudinal analysis, such as Laplace, Gaussian quadrature, and various linearization methods, and each method specifies a unique estimating procedure. In
Section 8.3, a variety of those methods will be described.
Given various estimating procedures for GLMMs,
ˆβ
is asymptotically normal, given the large-sample approximation to the joint distribution of parameters, with mean
0 and variance–covariance matrix
I(ˆβ)−1
. This asymptotic distribution facilitates testing of hypotheses on
ˆβ
by applying the standard approaches. For example, given H
0:
ˆβ=β
, the Wald statistic may be used to test
ˆβ
, given by
(ˆβ−β)′I(ˆβ)(ˆβ−β)∼χ2M,
 (8.29)
(8.29)where
I(ˆβ)
is the asymptotically consistent estimator for the expected information matrix
I(β)
, analogous to the specification in linear mixed models.
Similarly, the standard likelihood ratio statistic, which compares the likelihoods between two models with different parameter spaces, can be used to test the null hypothesis either on H
0:
β=ˆβ
for all components in
ˆβ
or on H
0:
θm =
βm=ˆβm
for a single component in
ˆβ
. The likelihood ratio statistic is given by
Λ=2l(ˆβ)−2l(β),
 (8.30)
(8.30)where
l(
β) is the log-likelihood function for the model without one or more parameters, and
l(ˆβ)
is the log-likelihood function containing all parameters. The likelihood ratio statistic,
Λ, is also asymptotically distributed as
χ2(M)
. Consequently, statistical testing on the fixed effects can be conducted with larger values of
Λ associated with smaller
p-values, thereby providing more evidence against H
0. Specifically, if
Λ is associated with a
p-value smaller than
α, the null hypothesis about
ˆβ
should be rejected; if it is associated with a
p-value equal to or greater than
α, the null hypothesis about
ˆβ
is accepted.
To summarize, hypothesis testing on the fixed effects in GLMMs can be performed by using the likelihood ratio test, the Wald statistic, or the score test. Between the likelihood ratio and the Wald statistics, the likelihood ratio statistic is considered to provide more reliable test results although it is computationally more complex. Therefore, the likelihood ratio test is preferable to test a null hypothesis on the fixed effects. The availability of various statistical software packages facilitates the application of the classical likelihood ratio test on the results of GLMMs.
8.2.4. Hypothesis testing on variance components
When the significance test is performed on the variance–covariance components of the random effects, some mixture distributions need to be used to test the null and the alternative hypotheses that
H0:σ2b˜i=0
and
H1:σ2b˜i>0
, where
σ2b˜i
is the
˜ith
element in
G. As indicated in
Chapter 4, the parameter space for a variance–covariance component of
G has open interval (0, ∞), and therefore, the hypotheses are tested on the boundary of the parameter space (
Verbeke and Molenberghs, 2003). As a result, the conventional tests, such as the likelihood ratio and the Wald statistics, cannot be directly applied to test the significance of the elements in
G. As the
G matrix in GLMMs is generally specified to follow multivariate normality, the procedures described in
Section 4.5 can be borrowed to approximate a mixture of distributions for the significance test of elements of
G in GLMMs.
Some statisticians propose the score tests, both two-sided and one-sided, to test the variance–covariance components of the random effects in GLMMs (
Hall and Præstgaard, 2001;
Jacqmin-Gadda and Commenges, 1995;
Lin, 1997;
Lin and Breslow, 1996;
Silvapulle and Silvapulle, 1995). In these approaches, the researcher can routinely assess the significance of the covariance structure against the ordinary fixed-effects null model. If no significant improvement is obtained from the inclusion of the random effects, the hypothesized GLMM model would be considered unnecessary. One of the advantages in this test is that it does not require the MLE in GLMMs because its approximations to the score function and the information matrix are derived under the null hypothesis of homogeneity. Such techniques are considered to be less powerful than the test based on the random effects model (McCulloch et al., 2008).
8.3. Methods of estimating parameters in generalized linear mixed models
In the analysis of nonnormal longitudinal data, such as proportions or counts, numerical integration or Bayes-type techniques are required to conduct a full ML analysis based on the joint marginal distribution. There are a variety of methods for the estimation of the parameters in GLMMs, with each using a unique approach on numerical approximation of the random effects. In this section, five commonly used families of such approximation techniques are described: the penalized quasi-likelihood
(PQL) method, the marginal quasi-likelihood (MQL) technique, the Laplace approximation, Gaussian quadrature rules, and the Markov Chain Monte Carlo (MCMC) approaches. The first two methods are expressed in terms of the Taylor series expansions, generally referred to as linearization methods. In contrast, the third, fourth, and fifth approaches are designed to approximate the log-likelihood of GLMMs, generally called the integral approximation methods. Both types of approximation have their respective advantages and limitations. The Expectation–Maximization (EM) method, another popular approximation approach, is not included in this section given a lengthy delineation of this method in
Chapter 4.
8.3.1. Penalized quasi-likelihood method
PQL derives the pseudo-likelihood estimates of model parameters based on the assumption that the regression parameters
β and
b are known and are equal to the current estimates
˜β
and
˜b
. Given this hypothesis, the parameters are estimated by the ML approach given multivariate normality of the pseudo data. By implementing this pseudo-likelihood approach,
β and
b are estimated from the linear mixed model equations, and the unknown parameters in
G and
R can be estimated either by the ML or by the restricted maximum likelihood (REML) estimator (
Wolfinger and O’Connell, 1993). Practically, the procedure is to estimate the fixed and the random parameter components separately and then iterate until the convergence criterion is met.
Let
A be the
ni ×
ni diagonal variance matrix evaluated at
μi of a known variance function. From Equation
(8.18), the following equation specifies the expectation of the nonlinear response variable conditionally on a matrix of the random effects
b:
E(y|b)=μ=g−1(X′β+Z′b+ɛ)=g−1(η),
 (8.31)
(8.31)where
b∼N(0,G)
. The variance of
y conditionally on
b is given by
var(y|b)=φA1/2R(˜α)A1/2.
 (8.32)
(8.32)According to
Wolfinger and O’Connell (1993), the first-order Taylor series expansion of
μ about
˜β
and
˜b
yields approximation of mean
g−1(η)=g−1(˜η)+˜∆X′(β−˜β)+˜∆Z′(b−˜b)+ε,
 (8.33)
(8.33)where
˜∆
is the diagonal matrix of the derivatives of the conditional mean evaluated at the expansion, mathematically defined by
˜∆=[∂ g−1(η)∂η]˜β,˜b.
By rearranging terms, the following expression is derived:
˜∆−1[μ−g−1(˜η)]+X′˜β+Z′˜b=X′β+Z′b.
 (8.34)
(8.34)The left side of Equation
(8.34) can be regarded as the expected value of the pseudo-response variable conditionally on
b, denoted by
˜y
, given by
˜∆−1[y−g−1(˜η)]+X′˜β+Z′˜b≡˜y,
 (8.35)
(8.35)and
var(˜y|b)=˜∆−1A1/2R(˜α)A1/2˜∆−1.
 (8.36)
(8.36)Therefore, a GLMM model can be formulated by
˜y=˙Xβ+Z′b+˜ε,
 (8.37)
(8.37)where
˜ɛ=˜∆−1[˜y−g−1(˜η)],
and this pseudo-error term
˜ɛ
is assumed to follow a normal distribution with zero expectation. Therefore, we can specify
˜y|β,b∼N(X′β+Z′b,˜∆−1A1/2R(˜α)A1/2˜∆−1).
 (8.38)
(8.38)Equation
(8.37) takes the form of a linear mixed model with the pseudo-response variable
˜y
, the fixed effects
β, the random effects
b, and
var(˜ɛ)=var(˜y|b)
. Given such specifications, the estimation of parameters can be performed by following the standard procedures for fitting a linear mixed model. Given starting values of
β,
G, and
φ in the marginal likelihood, the empirical Bayes estimates can be computed for
b, thereby generating the pseudo-data
˜y
. Consequently, the approximate linear mixed model can be fitted, yielding updated estimates for
β,
G, and
φ. The iterative process continues until a convergence criterion is reached.
Given the specifications of the two random components, the variance–covariance matrix for this model is given by
V(˜θ)=ZGZ′+˜∆−1A1/2R(˜α)A1/2˜∆−1,
 (8.39)
(8.39)where
˜θ
contains the unknown parameters in
G and
R.
Given a penalty term on the random effects, the estimates from optimizing a quasi-likelihood function on
˜y
are referred to as PQL estimates by
Breslow and Clayton (1993). Correspondingly, the approach for deriving such estimates is called PQL. The application of PQL can be based either on the maximum log pseudo-likelihood or on the restricted log pseudo-likelihood function for the pseudo-response variable
˜y
. Both estimators, ML or REML, can be performed in SAS by the PROC GLIMMIX procedure, as associated with a specific link function. The reader interested in learning more details about PQL is referred to
Breslow and Clayton (1993) and
Wolfinger and O’Connell (1993).
8.3.2. Marginal quasi-likelihood method
The regression structure in Equation
(8.31) is conditional on the value of the random effects
b. While the random effects are unobserved and are often of no direct interest, researchers are often more interested in the covariates’ effects on the nonlinear response than in the form of a specific distribution of the random effects. Therefore, some scientists consider it more appropriate to specify GLMMs in terms of the marginal mean, given by
E(y)=μ=g−1(X′β+ɛ).
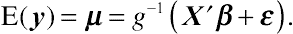 (8.40)
(8.40)Equation
(8.40) specifies a crude, first-order approximation to a GLMM that is considered valid in the limit as the components of dispersion approach zero (
Goldstein, 1991). In the longitudinal setting, given the presence of the random effects, an appropriate approximation about the mean may be specified:
y≈g−1(X′β)+˜∆Z′b+ε,
 (8.41)
(8.41)with corresponding variance
var(y)≈V0+˜∆−1Z′GZ˜∆−1,
 (8.42)
(8.42)where b ∼ N(0, G), and V0 is the diagonal matrix of within-subject variance, written as
V0=φA1/2R(X′β)A1/2.
 (8.43)
(8.43)Let
μ=(μ1,...,μN)′
be a marginal mean vector and
˜θ
be an unknown vector of all variance–covariance components. Using the quasi-likelihood equations appropriate for the response variable, the regression coefficients
β in the marginal model can then be estimated by solving the following estimating equation
˜U(β,˜θ)=∂ μ∂ β V−1(y)(y−μ)=0,
where
˜U(β,˜θ)
denotes the score statistic vector, mathematically defined as the first partial derivative of the log-likelihood function with respect to
β and
˜θ
. The inference of the quasi-likelihood functions is provided in
Appendix C.
Analytically, the equation can be further expanded to
X′(˜∆V0˜∆+Z′GZ′)−1˜∆(y−μ)=0.
 (8.44)
(8.44)Given the above specifications, this model specifies the linear predictor
η=(η1,...,ηN)′
as the vector of linear predictors
ηi=X′iβ
, and Fisher scoring is thought to result in the regression
y=η+˜∆(y−μ)
on
X with the weight matrix
V−1=(˜∆V0˜∆+Z′GZ′)−1.
 (8.45)
(8.45)Consequently, by optimizing a quasi-likelihood function that only includes the first- and the second-order moments, the MQL estimates can be derived. In other words, the information of the random effects is thought to be reflected in the variance–covariance matrix of the marginal mean. Therefore, without the specification of the random effects, this marginal approach is considered not to affect the estimation of regression coefficients. Given the marginal features, the model is referred to as the MQL. According to
Goldstein (1991), the estimation of
β is the same either with
ɛ=N(0,˜∆V0˜∆)
or with
b=N(0,G)
. Given such properties, this quasi-likelihood approximation technique based on linearization only concerns the mean of the random effects, with the estimates evaluated in the marginal linear predictor
X′ijˆβ
rather than in the conditional linear predictor
X′ijˆβ+Z′ijˆbi
. In SAS, the MQL method can also be performed by the PROC GLIMMIX procedure.
There are some technical issues with MQL in addition to those shared with PQL. As
Breslow and Clayton (1993) comment, unless the link function is the identity, the marginal mean defined by Equation
(8.40) does not generally coincide with the marginal mean specified by
(8.31) due to misspecification of the mean. Specifically, while it is reasonable to specify zero expectation in residuals of the linear predictor, the mean of the retransformed residuals on the nonlinear response is often not exp(0) = 1. Rather, it should be specified as the expectation of a specific posterior predictive distribution on the nonlinear response given the specified prior distribution. Failure to specify a full set of the random terms can result in erroneous nonlinear predictions of
y. In the analysis of nonlinear longitudinal data, MQL is valid only when
b = 0.
Liang and Zeger (1986) and Zeger et al. (1988) developed the GEEs that improve the MQL approach. In the succeeding texts, discussions about the marginal models will continue.
8.3.3. The Laplace method
Both the penalized and the MQL methods are based on pseudo data. Given such restrictions, the fixed effect estimates and the variance–covariance approximates can be associated with considerable bias, particularly in nonlinear predictions. Therefore, the analytic results derived from the linearization methods should be interpreted with great caution (
Molenberghs and Verbeke, 2010;
Rodriguez and Goldman, 1995). Some statisticians have suggested the use of the Laplace method to estimate the marginal posterior densities and the predictive distributions (
Lindstrom and Bates, 1990;
Shun, 1997;
Tierney and Kadane, 1986;
Wolfinger, 1993). The Laplace method is a statistical technique for approximating integrals of the form
∫⌢b⌢aexp[Nf(z)]dz,
 (8.46)
(8.46)where f(z) is some known, smooth function that is unimodal with a maximum at z0, and N is the sample size. Therefore, z0 is assumed to be the only point satisfying
∆f(z)=[∂f(z)∂z⌢a,∂f(z)∂z⌢a+1,...,∂f(z)∂z⌢b]=0.
It is also assumed that the Hessian matrix of f(z) at z0,
H′0=[∂2f(z)∂zi∂zj]|z=z0,
is positive definite. According to Taylor’s theorem, f(z) can be further expanded to the expression
f(z)=f(z0)+f′(z0)(z−z0)+12f′′(z0)(z−z0)2+O[(z−z0)3],
 (8.47)
(8.47)where
O[(z−z0)3]p0
.
Suppose that
z0 is not an endpoint and
f′′(z0)<0
. As
f′(z0)=0
given the above-specified conditions,
f(
z) can be approximated to the quadratic form
f(z)=f(z0)−12f′′(z0)(z−z0)2.
 (8.48)
(8.48)The above Laplace specifications can be readily extended to the longitudinal setting. For example, the marginal distribution of longitudinal data can be expressed as
p(y)=∏Ni=1p(yi)=∏Ni=1∫p(yi|bi)p(bi)dbi =∏Ni=1∫exp{log[p(yi|bi)p(bi)]}dbi =∏Ni=1∫exp{∑nij=1log[p(yij|bi)]+nilog[p(bi)]}dbi.
 (8.49)
(8.49)As indicated earlier, bi ∼ (0, G).
After some algebra, the Laplace approximation to the marginal log-likelihood can be written as
l(β,˜θ;ˆb,y)=∑Ni=1[∑nij=1log[p(yij|bi)]+nilog [p(bi)]+12nbilog(2π)−log|−12nif′′(β,˜θ;ˆbi)|],
 (8.50)
(8.50)where
nbi
is the common dimension of the random effect
bi.
Maximizing the above log-likelihood function with respect to
β,
˜θ
, and
b yields the MLE of the Laplace method parameters. There are different approaches in the optimization process for finding the appropriate estimates in the application of this integral approximation method. The reader interested in learning more details of those approaches is referred to
Pinheiro and Bates (1995) and
Wolfinger (1993).
The Laplace method is considered to fit better on nonlinear longitudinal data than both the conditional and the marginal pseudo-likelihood methods, especially when the sample size and the number of observations per subject are increased.
Even when the dimension of the integral increases with the sample size, the Laplace approximation has smaller bias than the pseudo-likelihood estimates (
Shun, 1997), thereby being highly applicable in longitudinal data analysis.
8.3.4. Gaussian quadrature and adaptive Gaussian quadrature methods
In deriving parameter estimates in GLMMs, a complex issue is the evaluation of the log-likelihood function as a multiple integral. In most situations, the integral does not have a closed form expression, as indicated earlier. In addition to the Laplace method, a widely used approximation method of the integral in GLMMs is Gaussian quadrature (
Pinheiro and Bates, 1995). The classical Gaussian quadrature is used to approximate integrals of given functions by a weighted sum of functional evaluations at selected abscissas or quadrature points. As an adaptation of the classical Gaussian quadrature rule to GLMMs, the adaptive Gaussian quadrature is a technique to approximate integrals that are centered about the empirical Bayesian estimates of the random effects. Given the approximation, the number of quadrature points can be selected given a desired standard of accuracy.
Suppose that there is a known, smooth function f(z) and a probability density function p(z). The function f(z) can then be integrated against p(z). The corresponding quadrature rule is
∫∞−∞f(z)p(z)dz≈∑Qq=1wqf(zq),
 (8.51)
(8.51)where
Q represents the number of quadrature points,
wq is the quadrature weight (
q = 1, …,
Q), and
zq is the abscissas, statistically referred to as a
node. In the context of GLMMs,
f(
z) can be regarded as the conditional distribution of longitudinal data given the random effects, and
p(
z) represents the random-effects distribution, respectively. Therefore, the reader not highly familiar with high-level mathematics might want to understand the quadrature approximate as a weighted average. Given such specifications, Equation
(8.51) conforms to Equation
(8.23) as a likelihood function.
In Gaussian quadrature and adaptive Gaussian quadratures,
p(
z) in Equation
(8.51) is defined as the density of the standard normal distribution. In longitudinal data analysis, the random effects may first be standardized as following a standard multivariate normal distribution with mean
0 and the identity covariance matrix, given by
⌢bi=G−1/2bi,
 (8.52)
(8.52)where
⌢b∼N(0,I)
is the standardized matrix of the random effects. Correspondingly, the variance component of the between-subjects random effects can be specified in the linear predictor, given by
ηi=X′iβ+Z′iG1/2bi.
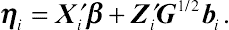 (8.53)
(8.53)Given the above specification, the likelihood contribution for subject i is
fi(yi|β,G,φ)=∫∏nij=1fij(yij|β,bi,φ)f(bi|G)dbi =∫∏nij=1fij(yij|β,⌢bi,G,φ)f(⌢bi)d⌢bi.
 (8.54)
(8.54)Equation
(8.54) is the formulation required to apply the Gaussian quadrature or adaptive Gaussian quadrature method (
Molenberghs and Verbeke, 2010). The classical Gaussian quadrature is approximated by the direct use of Equation
(8.51). Specifically, it chooses abscissas in areas of high density, and when
p(
z) is continuous, the quadrature rule is exact if
f(
z) is a polynomial of up to 2
Q − 1. Empirically, the number of quadrature points can be increased or decreased as desired, as briefly indicated in
Chapter 7. In principle, a higher number of quadrature points improves the accuracy of the approximation; in the meantime, however, it increases the computational burden.
Given the selection of the number of quadrature points Q, zq and weights wq can be found in some standard tables or obtained by some specific algorithms. A widely used algorithm, as is used in SAS, is the Gauss–Hermite quadrature. This numerical quadrature is an extension of the classical Gaussian quadrature to approximate the value of integrals in the form
∫∞−∞exp(−z2)f(z)dz≈∑Qq=1˜wqf(zq),
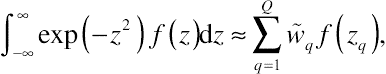 (8.55)
(8.55)where zq, with respect to the Gauss–Hermite quadrature, serves as the roots of the Hermite polynomials HQ(z), and
˜wq=2Q−1Q!√πQ2[HQ−1(zq)]2.
For details about Hermite polynomials and other forms of Gaussian quadrature, the interested reader is referred to
Stoer and Bulirsch (2010).
In the analysis of nonlinear longitudinal data, the density f(z) often takes the form of an exponential function, and therefore, some quadrature points zq may lie out of the region of interest. In the application of the adaptive Gaussian quadrature, the abscissas can be centered and rescaled, and therefore, the function f(z)p(z) follows a normal distribution. This adaptation ensures that more quadrature points lie in the region of interest. Technically, the adaptive Gaussian quadrature for the entire integral over bi centers the integral at the empirical Bayes estimate of bi that minimizes
−log[f(yi|xi,bi,φ)p(bi|G)]
with φ and G set equal to their current estimates. The final Hessian matrix from this optimization can be used to scale the quadrature abscissas.
Let (zq, wq; q = 1, …, Q) be the standard Gauss–Hermite abscissas and weights. The adaptive Gaussian quadrature integral approximation is then given by
∫f(yi|Xi,bi,φ)p(bi|G)dbi≈2nb/2|˜Γ(Xi,˜θ)| −1/2∑Qq1=1...∑Qqnb=1[f(yi|Xi,cq1,...,qnb,φ)f(cq1,...,qnb|G)∏nbr=1wqrexp(z2qr)],
 (8.56)
(8.56)where
nb is the dimension of
bi,
˜Γ(Xi,˜θ)
is the Hessian matrix from the empirical Bayes minimization, and
cq1,...,qR=⌢bi+2−1/2|˜Γ(Xi,˜θ)|−1/2zq1,...,qR.
Maximizing the log form of Equation
(8.56) over all subjects yields the ML estimates of the mode parameters given a standardized quadratic form. As the adaptive Gaussian quadrature is fitted to the observed data, the standard Wald, the likelihood ratio, and the score tests on parameter estimates can be applied effectively. One distinct advantage to applying the Gaussian quadrature is the use of the likelihood ratio statistic as an efficient tool for the evaluation of the overall fit in GLMMs. As indicated earlier, the PQL and MQL models are fitted on the pseudo data from linearization of nonlinear functions, from which the information about likelihoods is not trustworthy. The application of the Gaussian quadrature methods, however, may encounter numeric problems when the dimension of the random effects is complex.
To summarize, a
Q-point Gaussian quadrature rule provides an approximation of the definite integral of a distributional function, usually expressed as a weighted sum of functional values at specified points within the domain of an integral. The resulting integral can be evaluated accurately, thereby yielding unbiased and efficient estimates of the fixed and the random effects (McCulloch et al., 2008;
Molenberghs and Verbeke, 2010). In SAS, both the PROC GLIMMIX and the PROC NLMIXED procedures can be applied to fit nonlinear ML estimates, fixed and random, with either Gaussian quadrature or adaptive Gaussian quadrature. In applying the two Gaussian quadrature techniques, the estimates of the random effects depend heavily on the quality of starting values given the complex process of optimization in executing these procedures. Therefore, before the optimization process starts, a suboptimization needs to be performed from which initial empirical Bayes estimates of the random effects must be obtained first. The recommended approach is to run the PROC GLM procedure to obtain the starting values of the fixed effects and the PROC GLIMMIX procedure to obtain approximates of the random effect parameters. Examples of this practice will be provided in succeeding chapters.
Given the results of adaptive Gaussian quadrature, the number of quadrature points can be statistically determined by evaluating the log-likelihood function at the starting values of the parameters until two successive evaluations have a relative difference less than the current number of the quadrature points. It may be indicated that when Q = 1, z1 = 0, the adaptive Gaussian quadrature reduces to the Laplace approximation.
8.3.5. Markov Chain Monte Carlo methods
There are some other approximation methods that have also seen applications in the analyses of nonlinear longitudinal data. In addition to EM, some researchers have applied MCMC techniques such as the Metropolis–Hastings algorithm and the Gibbs sampling. In this section, these two MCMC methods are briefly described.
MCMC, as its name suggests, is a body of methods for generating pseudo-random draws from probability distributions by means of Markov Chains (
Schafer, 1997). The original Monte Carlo approach, developed by physicists to approximate integrals, defines a complex integral as an expectation of
f(
Y) over the density
p(
Y). Let a large number
Y1, …,
Yn of random variables be drawn from the density. The Monte Carlo integration is then given by
∫ba˜h(Y)dY=∫baf(Y)p(Y)dY=Ep(Y)[f(Y)]≅1n∑ni=1f(Yi),
 (8.57)
(8.57)where
∫∞−∞˜h(Y)dY
is a complex integral. Let
ˆ˜H(Y)
be the approximated integral. Then, the estimated Monte Carlo standard error can be written as
se[ˆ˜H(Y)]=√1n{1n−1∑ni=1[f(Yi)−ˆ˜H(Y)]2}.
 (8.58)
(8.58)In the analysis of nonlinear longitudinal data with the specified random effects, the Monte Carlo integration, as a Bayes-type technique, can be used to approximate marginal posterior distributions given the assumption of a Markov Chain process. Both the Metropolis–Hastings algorithm and the Gibbs sampler are typical applications of the Markov Chain techniques. In those approaches, attempts are made to draw samples from some distributions. In terms of the Metropolis–Hastings algorithm, the goal is to draw samples from a probability distribution to approximate the distribution of interest and then accept or reject the drawn value with a specified probability (
Metropolis et al., 1953; Hastings, 1970). The original Metropolis algorithm starts with some initial value
θ0 that satisfies
f(θ0)>0
. Using the current
θ value, a candidate point
θ* is then sampled from a jumping distribution
˜q(θ1,θ2)
, which is the probability of returning a value of
θ2 given a previous value of
θ1. In the Metropolis algorithm, the only restriction on the jumping density is that it is symmetric, and therefore,
˜q(θ1,θ2)=˜q(θ2,θ1)
. Given the candidate point
θ*, one can compute the ratio of the density at the candidate
(θ*)
and current
(θj−1)
points, denoted
⌢α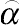
and given by
⌢α=p(θ*)p(θj−1)=f(θ*)f(θj−1).
The measurement
⌢α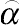
provides a standard for accepting or rejecting the candidate point. If the jump increases the density
(⌢α>1)
, accept the candidate point
(θj=θ*)
and return to the step of selection. If the jump decreases the density
(⌢α<1)
, with probability
⌢α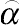
accept the candidate point, otherwise reject it and return to the step of selection. Therefore, in the application of the Metropolis sampling, one should first compute the value of
⌢α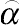
given by
⌢α=min[f(θ*)f(θj−1),1],
 (8.59)
(8.59)and then accept a candidate point with the probability of a move (
⌢α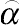
).
Hastings (1970) generalizes the above algorithm by using an arbitrary transition probability function
˜q(θ1,θ2)=Pr(θ1→θ2)
and setting the acceptance probability for a candidate point as
⌢α=min[f(θ*)˜q(θ*,θj−1)f(θj−1)˜q(θj−1,θ*),1].
 (8.60)
(8.60)Equation
(8.60) is referred to as the Metropolis–Hastings algorithm. The use of this algorithm is based on the scenario that if
⌢α>1
, the value of the candidate point
θ* is accepted and the equation
θj=θ*
is set; if
⌢α<1
, the value of
θ* is randomly accepted as the next iterate
θj with probability
⌢α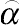
, and otherwise, keep the current value
θj=θj−1
.
The Gibbs sampler, perhaps the most popular MCMC method, was originally developed by mathematical physicists in image processing (
Geman and Geman, 1984) and later introduced and formalized into the realm of statistics by
Gelfand and Smith (1990). This approach can be regarded as a special case of the Metropolis–Hastings algorithm where the random value
θ* is always accepted (
⌢α=1
). Specifically, the Gibbs sampler draws samples from the conditional distribution of each component of a multivariate random variable given the other components in a cyclic fashion. The primary feature of this method is such that only univariate conditional distributions are considered. Compared to the Metropolis–Hastings algorithm, the specification of univariate conditional distributions is far easier to simulate than that of complex joint distributions with simple forms. In practice, one only needs to simulate
n random variables sequentially from
n univariate conditions rather than generate a single
n-dimensional vector by specifying a full joint distribution.
For practical purposes, the procedure of performing the Gibbs sampler is described below by borrowing the specification from
Gelfand and Smith (1990). Suppose that three variables,
X,
Y, and
Z, are considered and the conditional distribution of each is denoted by
(X|Y,Z)
,
(Y|X,Z)
, and
(Z|X,Y)
, respectively. The joint distribution is denoted by
(X,Y,Z)
, assumed to be positive over its entire domain for ensuring the full determination of the joint distribution by the three conditions. The Gibbs sampler considers a sequence of conditional distributions to generate a random variate
(X,Y,Z)
. With arbitrary starting values
X(0)
,
Y(0)
,
Z(0)
,
X(1)
can be drawn from
(X|Y(0),Z(0))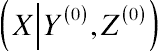
,
Y(1)
from
(Y|X(0),Z(0))
, and
Z(1)
from
(Z|X(0),Y(0))
, respectively. After a large number
˜n
of iterations,
(X,Y,Z)
is approximated by
(X(˜n),Y(˜n),Z(˜n))
. As
˜n→∞
, the joint distribution of
(X(˜n),Y(˜n),Z(˜n))
converges in probability at an exponential rate to
(X,Y,Z)
(
Geman and Geman, 1984). Consequently, given the joint distribution uniquely defined, the Gibbs sampler can extract the marginal distributions from the full conditional distributions.
In GLMMs, the Gibbs sampler can be applied to approximate the joint distribution
(β,G,b|y)
from the marginals
(β,G|y)
and
(bi|y)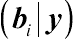
. By extending the above specifications, the joint distribution can be obtained from sampling the conditional distributions with a predetermined value of
˜n
. In SAS, the PROC MCMC procedure provides a flexible, simulation-based procedure for applying the Gibbs sampler given the specification of a likelihood function for the data and a prior distribution for parameters. The Gibbs sampler, together with other MCMC methods, however, is not considered to be as statistically efficient and mathematically precise as the Gaussian quadrature and the Laplace techniques. For more details concerning various MCMC methods, the reader is referred to
Gelfand and Smith (1990),
Geman and Geman (1984),
Hastings (1970), Metropolis et al. (1953),
Schafer (1997),
Tanner and Wong (1987), and
Zeger and Karim (1991).
 (8.3)
(8.3) .
. (8.4)
(8.4) (8.5)
(8.5) (8.7)
(8.7) (8.8)
(8.8) (8.9)
(8.9) (8.10)
(8.10) (8.11)
(8.11)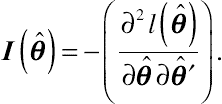 (8.13)
(8.13) (8.14)
(8.14) be a realization of a random variable Yi with mean μi and variance–covariance Vi. Suppose that g(yi, Xi) is a nonlinear function linking yi to the covariate vector Xi={Xi1,...,Xini}′
be a realization of a random variable Yi with mean μi and variance–covariance Vi. Suppose that g(yi, Xi) is a nonlinear function linking yi to the covariate vector Xi={Xi1,...,Xini}′ and a q × 1 vector of unknown individual random effects bi={bi1,...,biq}′
and a q × 1 vector of unknown individual random effects bi={bi1,...,biq}′ . In the construct of GLMMs, the function g(yi, Xi, bi) is assumed to be associated linearly with Xi and bi where g is a link function. The mean of the response variable for subject i at ni time points, namely μi, is then a modification of Equation (8.1) given the addition of the random effect vector bi, written as
. In the construct of GLMMs, the function g(yi, Xi, bi) is assumed to be associated linearly with Xi and bi where g is a link function. The mean of the response variable for subject i at ni time points, namely μi, is then a modification of Equation (8.1) given the addition of the random effect vector bi, written as (8.16)
(8.16) is the vector of within-subject random errors representing uncertainty in the response. The vector of within-subject random errors ɛi, conditionally on bi, is often assumed to have the property E(ɛi|bi)=0
is the vector of within-subject random errors representing uncertainty in the response. The vector of within-subject random errors ɛi, conditionally on bi, is often assumed to have the property E(ɛi|bi)=0 (8.22)
(8.22) (8.23)
(8.23) (8.24)
(8.24) (8.25)
(8.25) (8.26)
(8.26) (8.27)
(8.27) (8.28)
(8.28) . This asymptotic distribution facilitates testing of hypotheses on ˆβ
. This asymptotic distribution facilitates testing of hypotheses on ˆβ (8.29)
(8.29) is the asymptotically consistent estimator for the expected information matrix I(β)
is the asymptotically consistent estimator for the expected information matrix I(β) is the log-likelihood function containing all parameters. The likelihood ratio statistic, Λ, is also asymptotically distributed as χ2(M)
is the log-likelihood function containing all parameters. The likelihood ratio statistic, Λ, is also asymptotically distributed as χ2(M)

 (8.46)
(8.46)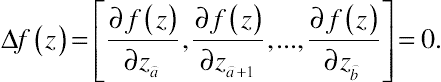

 (8.47)
(8.47) .
. (8.48)
(8.48) (8.49)
(8.49) (8.50)
(8.50) (8.51)
(8.51) (8.54)
(8.54)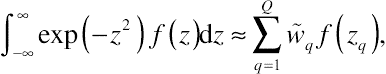 (8.55)
(8.55)
 (8.56)
(8.56) (8.57)
(8.57) (8.58)
(8.58)
 (8.59)
(8.59) (8.60)
(8.60)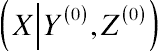 , Y(1)
, Y(1) , and Z(1)
, and Z(1) , respectively. After a large number ˜n
, respectively. After a large number ˜n