As described in
Chapter 3, given the desirable large sample property, maximization of the log-likelihood function on longitudinal data yields statistically robust and consistent estimates of the coefficient
β in linear mixed models. When the sample size is small, however, the ML estimator is criticized for failing to account for loss of the degrees of freedom in estimating
β, thereby resulting in downward bias in the variance estimate (
Patterson and Thompson, 1971). In those situations, the restricted maximum likelihood (REML) approach can be applied for correcting the bias. Compared to MLE, REML accounts for loss of the degrees of freedom in estimating the
variance components by using linear combinations of the error contrasts from the data. It then maximizes the likelihood function from the distribution of the linear combinations.
Harville (1974) proves from a Bayesian perspective that using only error contrasts to make inference on variance components is equivalent to ignoring any prior information on the fixed effects and using all the data. Given this proof, REML is recognized as an empirical Bayes method.
As summarized in
Chapter 3, inferences of linear mixed models consist of three estimating procedures: the fixed-effects parameters
β, the random effects
bi, and the variance–covariance components
R and
G. As briefly indicated in
Chapter 3, these procedures are often performed separately. I described the general specification and inference of the first and the third dimensions in the last chapter but not their computational details; neither the description of the second procedure of the inference – the estimation of the random effects
bi. As the specified random effects are not empirically observable, the estimation of
bi requires a complex approximation process. In some sense, it is appropriate to state that the random effects are predicted given the observed data and the fixed-effect estimates, rather than being estimated. In predicting the random effects, Bayes’ theory and the empirical Bayes techniques play an extremely important role.
In this chapter, Bayes’ theorem and Bayesian inference are reviewed first to help the reader understand the rationale of the REML estimator and the methods for approximating the random effects. The reader can also benefit from a brief overview of this methodology to set a solid foundation for comprehending various Bayes-type models and methods described in many of the succeeding chapters. Next, the general specifications and inference of the REML estimator are described. The third section presents two computational procedures for estimating parameters described in
Chapter 3 and in
Section 4.2: the Newton–Raphson (NR) and the Expectation–Maximization (EM) algorithms. The methods for approximating the subject-specific random effects are then delineated. Lastly, by following the two examples provided in
Chapter 3, analytic results derived from the ML and REML estimators are compared, and longitudinal trajectories of the response variables are predicted and displayed.
4.1. Overview of Bayesian inference
As it provides a flexible and practical approximating system, Bayesian inference and the associated algorithms have seen tremendous popularity in recent decades in longitudinal data analysis. With their widespread applications, Bayes formulations will be frequently used in the succeeding chapters when various Bayes-type techniques are described. Therefore, it is essential for the reader to grasp the basic concepts and the underlying properties of Bayesian inference described in this section before studying details of various Bayes-type models.
By definition, Bayesian inference is the process of fitting a probability model to a set of data
(Gelman et al., 2004). The inference summarizes the result by a probability distribution on the parameters of the model and on unobserved quantities such as predictions for new observations. Given such a capacity of using probability models,
Bayesian inference is valuable to quantify uncertainty in regression models, both generally and with specific regard to longitudinal data analysis.
In creating a Bayes model, the first step is to establish a joint distribution for all observable and unobservable quantities in a topic of interest. Let
y=(y1,y2,...,yN)
be a random vector of observed outcome data for
N units. If each unit has more than one observation, as in the case of longitudinal data, the dataset
y is specified as a random block vector denoted by
y=(y1,y2,...,yN)
. Let
⌢θ
be the unobservable vector of the population parameters (e.g., the subject-specific random effects in longitudinal analysis) and
X be a random matrix of the explanatory variables or covariates with
M columns. In Bayes theorem,
⌢θ
is expressed as a random vector estimated from data
y, which cannot be determined exactly. Given these conditions, uncertainty about
⌢θ
is expressed through probability statements and distributions. The probability statements are conditional on the observed outcome value
y and implicitly on the observed values of covariates
X, with the density of
⌢θ
written as
p(⌢θ|y)
. The function
p(⌢θ|y)
represents a conditional probability density with the argument determined by the observed data. With such probability statements on
⌢θ
, Bayesian inference can be described by three steps.
First, setting up a probability distribution of
⌢θ
, defined as
˜π(⌢θ)
, referred to, in the terminology of Bayesian inference, as the prior distribution or simply prior. The specification of the prior distribution depends on the researcher’s knowledge about the parameter before the data are examined (e.g., the normal distribution of the random effects in longitudinal data analysis).
Second, given the observed dataset
y, a statistical model is chosen to formulate the distribution of
y given
⌢θ
, written as
p(y|⌢θ)
.
Third, knowledge about
⌢θ
is updated by combining information from the prior distribution and the data through the calculation of
p(⌢θ|y)
, referred to as the posterior distribution. In a sense, the posterior distribution is simply the empirical realization of a probability distribution based on a prior.
The execution of the third step is based on the basic property of the conditional probability, referred as Bayes’ rule in Bayesian inference. Specifically, the probability density
p(⌢θ|y)
can be expressed in terms of the product of two densities, the prior distribution
˜π(⌢θ)
and the sampling distribution
p(y|⌢θ)
, referred to as a joint probability distribution and given by
p(⌢θ,y)=˜π(⌢θ)p(y|⌢θ).
The conditional probability of
⌢θ
given the known value of the data
y can be written as
p(⌢θ|y)=p(⌢θ,y)p(y)=p(y|⌢θ)˜π(⌢θ)p(y)=p(y|⌢θ)˜π(⌢θ)∫p(y|⌢θ)˜π(⌢θ)d⌢θ,
 (4.1)
(4.1)where the denominator in the third equality,
∫p(y|⌢θ)˜π(⌢θ) d⌢θ
, is the Bayes expression of
p(
y), assuming
⌢θ
to be continuous. In Bayesian inference, this expression is referred to as the marginal distribution of
y or the prior predictive distribution
(
Gelman et al., 2004). The specification of this term is the key to understanding Bayesian inference about fitting a probability model to data. To better understand the rationale of Bayesian inference, the reader not well-versed in calculus might want to view the data as the weighted average of a joint probability distribution with the prior of
⌢θ
(the discrete realization of an integral).
Given observed data
y, an unknown observable
˜y
can be predicted from the above inference. Let
y=(y1,y2,...,yN)
be the vector of the recorded values of an object weighed
N times on a scale and
⌢θ=(μ,σ2)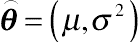
be the unknown value of the object with mean
μ and variance
σ2. Then, the distribution of
˜y
, given
y, is given by
p(˜y|y)=∫p(˜y,⌢θ|y)d⌢θ=∫p(˜y|⌢θ,y)p(⌢θ|y)d⌢θ=∫p(˜y|⌢θ)p(⌢θ|y)d⌢θ.
 (4.2)
(4.2)Given Equation
(4.2), the distribution or density of
˜y
is referred to as the posterior predictive distribution – posterior because it is conditional on the observed
y and predictive because it is a prediction for an observable
˜y
. The third equality in Equation
(4.2) reflects the posterior predictive distribution as an integral of the conditional predictions given the posterior distribution of
⌢θ
. This equation important in longitudinal data analysis because there is generally unobserved heterogeneity across subjects, and with the above inference it is practical to specify mixed-effects models in terms of the marginal mean given the distribution of the random effects. By viewing
⌢θ
as an unobservable parameter, the researcher can use Equation
(4.2) to express the marginal mean of a posterior predictive distribution with prior knowledge about the distribution of
⌢θ
. The reader might want to link this inference to longitudinal data analysis. The subject-specific random effects are specified as a prior to account for intraindividual correlation, and the marginal mean of the posterior predictive distribution is the prediction given the prior distribution.
In Bayesian inference, given a chosen probability model, the data
y affect the posterior inference only through the function
p(y|⌢θ)
, which, as a function of
⌢θ
given fixed data
y, is the likelihood function. The likelihood function of
⌢θ
can be any function proportional to
p(y|⌢θ)
, written as
L(⌢θ)∝p(y|⌢θ).
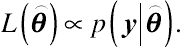 (4.3)
(4.3)With the above specification, a Bayes-type model can be expressed in terms of a likelihood function, given by
p(⌢θ,y)=L(⌢θ)˜π(⌢θ)∫L(⌢θ)˜π(⌢θ)d⌢θ,
 (4.4)
(4.4)where the denominator on the right of Equation
(4.4) is the likelihood expression of the marginal distribution
p(
y) as an integral. As long as the integral is finite, the value of the integral does not provide any additional information about the posterior
distribution. Correspondingly, the distribution of
⌢θ
given
y can be expressed as an arbitrary constant in a proportional form, given by
p(⌢θ|y)∝.L(⌢θ) ˜π(⌢θ).
 (4.5)
(4.5)To summarize, Bayesian inference starts with prior knowledge of the distribution for
⌢θ
and then updates the knowledge about the prior after learning information from the observed data
y. Empirically, all Bayesian inferences are performed from the posterior predictive distribution, namely
p(⌢θ|y)
. In longitudinal data analysis, if the researcher has prior information about the probability distribution of the subject-specific random effects, the distribution can be included in statistical inference by applying Bayesian inference. Various Bayes techniques can be applied to integrate the joint posterior distribution of all unknowns, and consequently, the desired marginal distribution can be obtained. It follows that the specified parameters of observed variables can be adequately estimated by including the unobserved quantities in a probability distribution. In statistics, the unknown quantities that are not of direct interest but are required in specifying a joint likelihood function are referred to as nuisance parameters. Most Bayesian methods require sophisticated computations, including complex simulation techniques and approximation algorithms.
4.2. Restricted maximum likelihood estimator
The maximum likelihood approach is perhaps the most popular fitting method in regression modeling. When the population mean is unknown, however, the maximum likelihood estimator for the variance σ2 is biased downward due to loss of the degrees of freedom in the estimation of the fixed effects. For small samples, it may be more appropriate to apply the REML estimator to derive unbiased estimates of variance and covariance parameters. In this section, I first display how the variance estimate is biased in the maximum likelihood estimator. Next, based on the discussion about the effect of the nuisance parameters, I describe statistical inference of the REML estimator.
4.2.1. MLE bias in variance estimate in general linear models
I begin with reviewing some basic statistics on the computation of sample variance with a sample of N subjects. With a known or an unknown population mean, denoted by μ, the variance estimate is computed differently, given by
ˆσ2={∑Ni=1(Yi−μ)2N if μ is known∑Ni=1(Yi−ˉY)2N−1 if μ is unknown}.
The above equation indicates that when
μ is unknown there is one degree of freedom lost in computing the sample mean
ˉY
. Such a loss in the degree of freedom needs to be corrected for, deriving an unbiased variance estimate. The corrected variance estimate given unknown
μ is statistically defined as the mean square error.
The above simple case can be extended to the inference of the MLE bias in the variance estimate in general linear models. Let all vectors of Yi, ɛi, and the matrices Xi be combined into Y, ɛ, and the matrices X, respectively. Then, a combined general liner model can be written as
Y=X′β+e,
where
e ∼ N(
0,Σ) and Σ is defined as an
N ×
N positive-definite variance–covariance matrix of random errors. The matrix Σ depends on the unknown parameters organized into a vector
˜Γ
, and given the specification of
β, this matrix is often simplified as
σ2I, where
I is the identity matrix, assuming random errors to be conditionally independent in the presence of the fixed-effect parameters. For Σ =
σ2I,
˜Γ≡σ2
. It follows that the classical MLE of
σ2, given the observed outcome data
y, is given by
ˆσ2=(y−X′ˆβ)′(y−X′ˆβ)N.
 (4.6)
(4.6)If the population mean
μ is unknown,
β needs to be estimated from the data first for deriving the sample mean
X′ˆβ
. Given
M degrees of freedom lost in
ˆβ
, the expectation of
σ2 becomes
E(ˆσ2)=N−MNσ2,
 (4.7)
(4.7)where
M is the dimension of
X, or the number of covariates if the model has full rank. Equation
(4.7) is the mean square error statistic, an unbiased estimator for
σ2. It can be mathematically proved that when
μ is unknown, Equation
(4.6) does not exactly correspond to Equation
(4.7), thereby yielding a biased estimate of
σ2. Below I provide a simple mathematical proof.
By contradiction, suppose
E(ˆσ2)=σ2
, given by
E[(y−X′ˆβ)′(y−X′ˆβ)N]=σ2.
 (4.8)
(4.8)It follows that
E[(y−X′ˆβ)′(y−X′ˆβ)N]=N−MNσ2<σ2=E[(y−X′ˆβ)′(y−X′ˆβ)N].
 (4.9)
(4.9)Obviously, Equation
(4.9) contradicts the condition that
E(ˆσ2)=σ2
. Therefore, the ML estimator for
σ2
is biased downward due to failure to account for loss of the degrees of freedom in the estimation of
μ given the estimates of
β. It is also clear from Equation
(4.9) that if
N is large and
M is relatively small, bias in MLE
ˆσ2
becomes negligible and thus can be overlooked.
4.2.2. Specification of REML in general linear models
The REML estimator is designed to correct for bias incurred from the classical MLE by avoiding the specification of β first in a simplified likelihood function. Specifically, REML maximizes a likelihood of a set of selected error contrasts, not of all the data, with the likelihood specified only in terms of Σ. The method starts with the construction of error contrasts with zero expectation, and maximization of the corresponding joint likelihood is then performed for yielding unbiased parameter estimates.
As indicated earlier, MLE of
σ2
is biased downward without an adjustment factor (
N −
M)/
N. For making a correction on this bias, the REML approach first specifies an
N-dimensional vector containing only ones, denoted by
1N. The distribution of
Y then can be written by
N(μ 1N,σ2IN)
(notice that
1 and the identity matrix
I are two different concepts). Let
⌢A={⌢a1,...,⌢aN−1}
be any
N × (
N − 1) matrix with
N − 1 linearly independent columns orthogonal to the vector
1N
. It follows that an
N × 1 vector of error contrasts is created, defined as
⌢U=⌢A′Y
. By definition,
⌢U
follows a normal distribution with mean
0 and covariance matrix
σ2⌢A′⌢A
. Maximizing the corresponding likelihood with respect to the only remaining parameter
σ2
gives
ˆσ2=Y′⌢A(⌢A′⌢A)−1⌢A′Y(N−1).
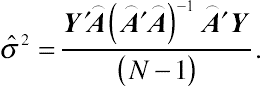 (4.10)
(4.10)Obviously, the above estimator is unbiased. Equation
(4.10) is the basic specification of the REML estimator.
Equation
(4.10) can be readily adapted to the estimation of
σ2
in general linear models. Given a linear regression
Y=X′β+e, 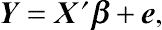
where
Y is an
N-dimensional vector and
X is an
N ×
M matrix with known covariate values. All elements in
e are assumed to be independent and identically distributed (iid) with zero expectation and variance
σ2
. Given the inclusion of the covariates,
⌢A={⌢a1,....,⌢aN−M}
is now any
N × (
N −
M) matrix with
N −
M linearly independent columns orthogonal to the columns of the design matrix
X. Accordingly, in general linear models, the vector of error contrasts
⌢U
is an (
N −
M) × 1 vector, given by
⌢U={⌢u1⋮⌢uN−M}={⌢a′1y⋮⌢a′N−My}=⌢A′Y,
 (4.11)
(4.11)where a given element in
⌢U
is
⌢a′iy
, which, by definition, is an error contrast if
E(⌢a′iy)=0
, and thereby
⌢a′ix=0′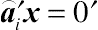
.
The vector
⌢U
follows a normal distribution with mean
0 and the newly structured covariance matrix
σ2⌢A′⌢A
, where
σ2
remains the only unknown parameter. Maximizing the corresponding likelihood with respect to
σ2
gives rise to the following estimator:
ˆσ2=[y−X(X′X)−1X′y]′[y−X(X′X)−1X′y]N−M,
 (4.12)
(4.12)which is the mean square error in the context of general linear models, unbiased for
σ2
. As a result, underestimation of MLE
σ2
is corrected. Therefore, the REML estimator is essentially a maximum likelihood approach on residuals. Additionally, from the specification
⌢U=⌢A′Y
, the following inference can be derived:
⌢U=⌢A′Y=⌢A′(X′β+e)=⌢A′X′β+⌢A′e=0+⌢A′e=⌢A′e,
where
⌢A′e∼N(0,⌢A′Σ⌢A)
.
After some additional algebra, the restricted log-likelihood function with respect to Σ for a sample of N subjects can be written as
lR(Σ|⌢U)=−N−M2log(2π)−12log|⌢A′Σ⌢A|−12⌢U′(⌢A′Σ⌢A)−1⌢U.
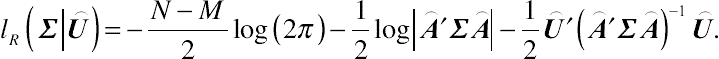 (4.13)
(4.13)Given the above inference, the REML estimator is a residual-based estimating method that integrates
β out. For this reason, this estimator is also referred to as the residual maximum likelihood or the modified maximum likelihood estimator (
Harville, 1974;
Patterson and Thompson, 1971).
4.2.3. REML estimator in linear mixed models
The above REML estimator for general linear models can be easily extended to linear mixed models by following the same approach of error contrasts. Combining vectors of
Yi
,
bi
, and
ɛi
and the matrices
Xi
into
Y,
b,
ɛ, and
X leads to
Y=X′β+Zb+e,
where
Z is the block diagonal matrix with blocks
Zi
on the main diagonal and zeroes off-diagonally. As formalized in
Chapter 3, the marginal distribution of
Y is normal with mean vector
X′β
and covariance matrix
V(R,G)
with blocks
Vi
on the main diagonal and zeroes off-diagonally. After some simplification, the classical log-likelihood function associated with MLE is
l(G,R)=−N2log(2π)−12log|V|−12⌢r′V−1⌢r,
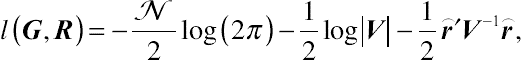 (4.14)
(4.14)where
⌢r=y−X′ˆβ
, defined as the vector of marginal residuals, which will be further discussed in
Chapter 6.
Maximization of the above log-likelihood function on the data yields an estimate of
β and
V(G,R)
. Analogous to the specification for general linear models, the diagonal elements in
V(G,R)
are underestimated for small samples due to loss of the degrees of freedom in estimation of the marginal mean
X′β
first. By extending the REML estimator for general linear models, such underestimation in variance estimates can be corrected.
The REML estimator for the variance components
R and
G in linear mixed models can be obtained from maximizing the log-likelihood function of a set of contrasts
⌢U=⌢A′Y
, where
⌢A
is any [
N × (
N −
M)] full-rank matrix with columns orthogonal to the columns of the
X matrix. The
⌢U
follows a normal distribution with mean vector
0 and covariance matrix
⌢A′V(R,G)⌢A
that integrates
β out. After some algebra, the joint restricted log-likelihood function with respect to parameter vectors
R and
G for a random sample of size
N is
lR(G,R)=−N−M2log(2π)−12log|V|−12⌢r′V−1⌢r−12log|X′V−1X|,
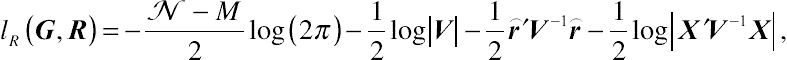 (4.15)
(4.15)where, given the standard formula,
⌢r=y−X′ˆβ=y−X(X′V−1X)−1X′V−1y.
Maximization of the above residual log-likelihood function on the transformed data of error contrasts yields an unbiased estimate of
V(G,R)
. In turn, Equation
(3.23) can be applied to estimate the vector
β (
Fitzmaurice et al., 2004).
By comparing Equations
(4.15) and
(4.14), there is one additional term in the REML log-likelihood, which is the last term on the right of Equation
(4.15). Expanding that term yields
−12log|X′V−1X|=12log|(X′V−1X)−1|=log|cov(ˆβ)|12,
which is the covariance of
ˆβ
. This additional term can be regarded as an adjustment factor for bias in
V(G,R)
from MLE. Correspondingly, the above restricted log-likelihood function can be expressed in terms of MLE plus an adjustment factor, given by
lR(G,R)≈l(G,R)+log|cov(ˆβ)|12.
 (4.16)
(4.16)Analogous to MLE, the REML estimator is based on the MAR hypothesis. Operationally, a maximum likelihood estimate of
V, derived either from MLE or
from REML, can be obtained through a specific iterative scheme, such as the NR
(Lindstrom and Bates, 1988) and the EM algorithms
(Dempster et al., 1977), which will be described in
Section 4.3.
4.2.4. Justification of the restricted maximum likelihood method
There is some debate concerning the validity of the REML estimator. At the first glance, some information seems lost by basing inferences of
G and
R on
lR rather than on
l.
Patterson and Thompson (1971) contend that for any vector of
N −
M linearly independent error contrasts, the log-likelihood function for the transformed data vector
⌢U=⌢A′Y
is proportional to the log-likelihood function for
y, so that inferences on
⌢A′Y
are valid as on
y. It actually makes no difference which
N −
M linearly independent contrasts are used because the log-likelihood function for any such set differs by no more than an additive constant
(Harville, 1977).
Harville (1974) found it attractive to use only error contrasts rather than all the data. Given this convenience, a prior distribution for
β does not need to be specified nor should analytic or numerical integrations be specified to determine the posterior distribution for
G and
R. For proving his argument,
Harville (1974) provides a justification of the REML estimator in general linear models by using Bayesian inference.
Let
⌢a′iy
be a linear combination of error contrasts such that
E(⌢a′iy)=0
and
⌢a′ix=0′
and the density of
⌢U
be
f⌢U(⌢A′Y|G,R)
. Given the familiar statistical expression of
β in linear regression models
β=(X′V−1X)−1X′V−1Y,
the estimate β can be rewritten as
ˆβ=⌢H′y,
 (4.17)
(4.17)where
⌢H
is defined as
⌢H=V−1X(X′V−1X)−1.
 (4.18)
(4.18)Using results on determinants in matrix algebra gives rise to
|det(⌢A,⌢H)|={det[(⌢A,⌢H)′(⌢A,⌢H)]}12=[det(1)]12[det(⌢H′⌢H−⌢H′⌢A1−1⌢A′⌢H)]12=[det(X′X)]−12.
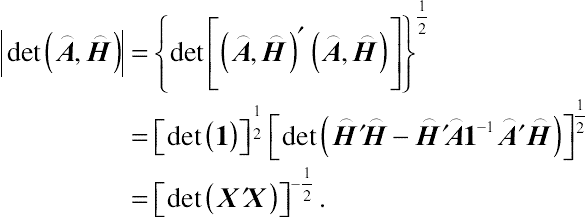 (4.19)
(4.19)Let
fˆβ(⋅|β,G,R)
and
fy(⋅|β,G,R)
be the probability density functions (p.d.f.) of
ˆβ
and
y, respectively. Given the well-known relationship
(y−X′β)′V−1(y−X′β)=(y−X′ˆβ)′V−1(y−X′ˆβ)+(β−ˆβ)′(X′V−1X)(β−ˆβ),
the Bayes-type expression about the likelihood of
⌢U
is then given by
f⌢U(⌢A′y|G,R)=∫f⌢U(⌢A′y|G,R)fˆβ(⌢H′y|β,G,R)dβ=[det(X′X)]12∫fy(y|β,G,R)dβ=(2π)−12(N−M)[det(X′X)]12[det(V)]−12[det(X′V−1X)]−12exp[−12(y−X′ˆβ)′V−1(y−X′ˆβ)].
 (4.20)
(4.20)Compared to Patterson and Thompson’s expression, Equation
(4.20) provides a more convenient perspective to derive the likelihood equations, thereby being preferable for numerical computation of the density
f⌢U(⌢A′y|G,R)
.
Let
f(G,R)
be the prior p.d.f. for the variance–covariance components
G and
R. When only the error contrasts are used, the posterior probability density for
G and
R is then written as
p(G,R|y)∝.f(G,R) f⌢U(⌢A′y|G,R).
 (4.21)
(4.21)Equation
(4.21) literally states that assuming
β and the variance components
(G,R)
to be statistically independent and the components of
β to be independent and identically distributed, the posterior density for
(G,R)
is proportional to the product of the prior density for
(G,R)
and the likelihood function of an arbitrary set of (
N −
M) linearly independent error contrasts. Therefore, from the standpoint of Bayesian inference, using only error contrasts to make inference on
(G,R)
is equivalent to ignoring any prior information on
β and using all the data to make these inferences. In other words, the REML estimator is identical to the mode of the marginal posterior density for
(G,R)
, formally integrating
β out.
4.2.5. Comparison between ML and REML estimators
Both ML and REML estimators are powerful estimating approaches with desirable properties of statistical consistency, asymptotic normality, and efficiency. It is traditionally regarded that MLE is associated with several advantages in linear regression modeling. As neither overestimating nor underestimating the corresponding population parameters, ML estimates are generally unbiased for large samples. The ML estimator is consistent as the parameter estimates converge in probability to the true value of the population parameters as the sample size increases, asymptotically following a multivariate normal distribution. When this large-sample behavior follows, the ML function approximates a chi-square distribution under the assumption of
multivariate normality, and accordingly, the model chi-square can be used to test the overall model fit. In linear mixed models, these statistical strengths usually remain effective in the estimation of the fixed effects and the variance components, as long as the sample size is sufficiently large. For small samples, however, these advantages in precision of using all the data may be negated to some extent by the additional approximation procedures to specify a complete prior distribution for
β,
G, and
R (
Harville, 1974, 1977). As indicated earlier, in theory the ML estimates of the variance components are biased downward due to loss of the degrees of freedom in estimating the fixed effects. From the Bayesian standpoint, when the prior distribution of
β is concentrated away from the true value of
β, the posterior distribution of
G and
R based on the complete data is adversely affected. In these situations, maximizing the likelihood based on error contrasts is effective.
In the application of linear mixed models, the REML estimator is often considered preferable over MLE as it corrects for loss of the degrees of freedom in MLE of the fixed effects (
Davidian and Giltinan, 1995;
Fitzmaurice et al., 2004;
Harville, 1977). If the sample size is sufficiently larger than the number of model parameters, however, the bias in MLE is negligible, and in such situations, the two estimators usually yield very close parameter estimates.
Harville (1977) compares the size of the estimated variances derived from the two estimators in the application of general linear models. The ML estimator of the variance
σ2
consistently yields smaller mean square errors than the REML estimator when
M = rank(
X) ≤ 4; by contrast, the REML estimator of the variance
σ2
has smaller mean square errors than MLE when
M = rank(
X) ≥ 5 and the size of
N −
M is sufficiently large. Therefore, when more fixed effects are specified, the difference between the ML and REML estimators of variance widens.
Notice that while it can be used to compare nested models for the covariance, the REML log-likelihood cannot be used to compare nested regression models for the mean (
Fitzmaurice et al., 2004). This is thought to be because the addition of the adjustment factor in the REML estimator, the last term on the right of Equation
(4.15), depends on the specification of a regression model. Therefore, the REML likelihood for two nested models for the mean response is based on different sets of error contrasts. If statistical assessment on the difference between two means is necessary, the researcher needs to use the ML estimator for estimating the two related nested regression models after carefully checking the statistical adequacy of using this classical estimator.
4.3. Computational procedures
In longitudinal data analysis, the maximum likelihood or the REML estimators cannot be expressed in a simple and closed form except in some special situations. Therefore, the ML and REML estimates of the parameters in G and R must be computed by applying numeric methods. In this section, two popular computational methods are described: the NR and the EM algorithms. Both methods are iterative schemes and have been widely applied in longitudinal data analysis.
4.3.1. Newton–Raphson algorithm
The NR algorithm is an iterative method for finding estimates for the parameters by minimizing −2 times a specific log-likelihood function. In applying this algorithm, both ML and REML log-likelihood functions can be used to estimate the variance components (
Laird and Ware, 1982;
Ware, 1985). The first step of the NR algorithm is to simplify the computational procedure by solving the ML and REML estimates of
σ2
as a function of
β,
G, and
R. In statistics, the procedure for reducing the dimension of an objective function by analytic substitution is referred to as profiling. In the NR algorithm, profiling is applied to ensure that the numerical optimization can be performed only over the model parameters. Given
quations (3.22) and
(4.15), the estimate of
σ2
can be simplified by
ˆσ2ML(β,G,R)=1Nr′V(G,R)−1r,
 (4.22)
(4.22)and
ˆσ2REML(β,G,R)=1N−Mr′V(G,R)−1r,
 (4.23)
(4.23)where
N=∑Ni=1ni
and
r=y−X′β
, both defined earlier.
The above two equations are then substituted into Equations
(3.22) and
(4.15). After some simplification, two corresponding profile log-likelihood functions of
β,
G, and
R can be specified:
PML(β,G,R|y)=−N2log(r′V(G,R)−1r)−12log|V(G,R)|,
 (4.24)
(4.24)PREML(β,G,R|y)=−N−M2log(r′V(G,R)−1r)−12log|V(G,R)|−12log|x′V(G,R)−1x|,
 (4.25)
(4.25)where
PML(⋅)
and
PREML(⋅)
are the profile log-likelihood functions for computing the ML and the REML estimates, respectively. According to
Lindstrom and Bates (1988), the NR optimization can be based either on the original log-likelihood or the profile log-likelihood function, but the latter is recommended as the profile log-likelihood usually requires fewer iterations for deriving estimates for
β,
G, and
R.
In the NR algorithm, a series of formulas are specified for the derivatives of the profile log-likelihoods in Equations
(4.24) and
(4.25) and with respect to
β,
G, and
R. These formulations enable an NR implementation. The derivatives for linear mixed models are computed with the conditionally independent errors, given by
Vi=σ2Vi(G,R)
. The chain rule (a rule in mathematics for differentiating compositions of functions) is used to find the derivatives for a specific mixed-effects model
with respect to the transformed
G and
R. The inverse of the second derivatives of the profile log-likelihood function at iterative convergence yields an estimate for the marginal variance–covariance matrix over the parameter space. If the residual variance
σ2
is a part of the mixed model, it can be profiled by analytically solving for the optima
σ2
and then plugging this expression back into the likelihood formula (
Wolfinger et al., 1994). The exact procedures for these formulas are complex, and the reader interested in the computational details concerning the first and second derivatives of
PML(β,G,R|y)
and
PREML(β,G,R|y)
is referred to the original articles in this regard (
Lindstrom and Bates, 1988;
Wolfinger et al., 1994).
Operationally, the estimation of
G and
R can be performed through a conventional NR iterative scheme, given some specified initial values for the parameter estimates. With regard to linear mixed models, the series of parameter estimates in the iterative scheme is generally denoted by
ˆθ˜j (¨j=1, 2, …)
(¨j=1, 2, …)
, where
θ consists of
β,
G, and
R. The iterative scheme terminates when
ˆθ˜j+1
is sufficiently close to
ˆθ˜j
given some statistical criterion. As a result, the maximum likelihood estimate of
θ can be operationally defined as
ˆθ=ˆθ˜j+1
.
The NR algorithm is widely considered to be a preferred computational method over other procedures in the application of linear mixed models given its desirable convergence properties and its capacity to derive information matrices. Sometimes, however, the researcher might encounter failure of convergence in the iterative processes or the occurrence of convergence at unrealistic parameter values when performing the NR algorithm. In general, such convergence problems occur much more frequently in the estimation of the variance components than in that of the fixed effects. In these situations, the researcher might want to consider specifying a different set of starting values for parameter estimates or using other numeric methods.
4.3.2. Expectation–maximization algorithm
The EM method is designed to estimate the unobserved parameters in regression models. Like the NR algorithm, the EM method can be applied to obtain both the ML and the REML estimates (
Laird and Ware, 1982). When MLE is applied, the covariance matrix can be estimated by using the classical EM algorithm described in Dempster et al. (1977, 1981),
Laird (1982), and
Laird and Ware (1982).
In longitudinal data analysis, the EM algorithm can be applied to approximate the unobserved subject-specific random effects by maximizing the likelihood function given the observed outcomes
y (
Laird and Ware, 1982). Given the estimates of
β,
G, and
R, the random effect for a specific subject can be obtained by the following equation:
ˆbi=ˆGZ′iˆV−1i(yi−X′iˆβ).
 (4.26)
(4.26)In Equation
(4.26),
Vi
is the overall variance–covariance matrix of
yi
, and its inverse,
V−1i
, is often used as a weight matrix in the estimation process to yield efficient
and robust parameter estimates. In this equation,
ˆbi
is computed as the proportion of the overall variance–covariance matrix that comes from the between-subjects variability times the overall residual from the marginal mean. Therefore, given the availability of
ˆG
and
ˆVi
,
ˆbi
can be readily computed. This estimator is efficient and robust because the fixed-effects estimate maximizes the likelihood based on the marginal distribution of the empirical data. The inference of Equation
(4.26) will be further presented in
Section 4.4.
Let
Ri=σ2I
and
G is an arbitrary
q ×
q nonnegative-definite covariance matrix. The variance
σ2
can then be written as
ˆσ2=∑Ni=1e′iei∑Ni=1ni=˜t1∑Ni=1ni,
 (4.27)
(4.27)and
ˆG=N−1∑Ni=1b′ibi=˜t2N,
 (4.28)
(4.28)where
ei
is an
ni × 1 column vector of model residuals for subject
i, as defined in
Chapter 3. According to
Laird and Ware (1982), the two terms of sum of squares,
˜t1=∑Ni=1e′iei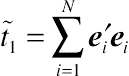
and
˜t2=∑Ni=1b′ibi
, are the sufficient statistics for
Ri and
G, respectively.
Let
Θ be an available estimate of
Ri and
G (notice that
Θ differs from
θ). The statistics
˜t1
and
˜t2
can then be calculated by using their expectations conditionally on the observed data vector
y, given by
ˆ˜t1=E{∑Ni=1e′iei|yi,ˆβ(ˆΘ),ˆΘ} =∑Ni=1{ˆei(ˆΘ)′ˆei(ˆΘ)+tr var[ei|yi,ˆβ(ˆΘ),ˆΘ]},
 (4.29)
(4.29)and
ˆ˜t2=E{∑Ni=1b′ibi|yi,ˆβ(ˆΘ),ˆΘ} =∑Ni=1{ˆbi(ˆΘ)′ˆbi(ˆΘ)+var[bi|yi,ˆβ(ˆΘ),ˆΘ]},
 (4.30)
(4.30)where
ˆei(ˆΘ)=E(ei|yi,ˆβ(ˆΘ),ˆΘ)=yi−X′iˆβ(ˆΘ)−Zibi(ˆΘ).
Operationally, the EM algorithm requires suitable starting values for
ˆRi
and
ˆG
and then iterate between Equations
(4.29) and
(4.30), referred to as the E-step (expectation step), and between Equations
(4.27) and
(4.28), referred to as the M-step (maximization step). At convergence of values in
˜t1
and
˜t2
after a series of iterations, the ML estimates of both the fixed and the random effects,
ˆΘML
,
ˆβ(ˆΘML)
, and
ˆb(ˆΘML)
, can be obtained from the last E-step.
The EM algorithm can also be applied to compute the REML estimates, denoted by
ˆΘREML
,
ˆβ(ˆΘREML)
, and
ˆbi(ˆΘREML)
, respectively, through an empirical Bayes approach. In the EM iterative series for the REML estimator, the M-step remains the same as iterating between Equations
(4.27) and
(4.28) because the estimation of
Θ is still based on
y,
β, and
e. The E-step in the REML estimator, however, differs from the procedure in MLE. While the E-step for MLE depends on
y and
β, the expectation with REML is only conditional on
y as
β is integrated out of the likelihood. Consequently, in REML Equations
(4.29) and
(4.30) are replaced with the following formulas:
ˆ˜t1=E{∑Ni=1e′iei|yi,ˆΘ} =∑Ni=1{ˆei(ˆΘ)′ˆei(ˆΘ)+tr var[ei|yi,ˆΘ]},
 (4.31)
(4.31)and
ˆ˜t2=E{∑Ni=1b′ibi|yi,ˆΘ} =∑Ni=1{ˆbi(ˆΘ)′ˆbi(ˆΘ)+var[bi|yi,ˆΘ]},
 (4.32)
(4.32)where
e′i(ˆΘ)
is still defined as
yi−X′iˆβ(ˆΘ)−Z′ibi(ˆΘ).
The expectations computed in the above E-step in the REML estimator involve the conditional means and variances of
bi
and
ei
. Theoretically, the variance estimates obtained from REML can differ from their ML counterparts that are biased downward, as indicated in
Section 4.2. For large samples, however, the bias in the ML estimates tends to be negligible, and therefore, the ML and the REML estimates are equally robust if the sample size is sufficiently large.
In summary, the EM algorithm is a simple and convenient approach for estimating the variance–covariance parameters. Given some desirable properties in this approach (
Dempster et al., 1977), the EM procedure has historically seen considerable applications in longitudinal data analysis. In many situations, however, the EM algorithm is regarded as a less preferable numerical method than the NR in several aspects. Its relatively weaker convergence properties are particularly criticized.
Lindstrom and Bates (1988) and Wolfinger et al. (1994) provide reasons for
this negative assessment on the EM algorithm. Consequently, the EM method has gradually become a less-applied computational algorithm than the NR approach in longitudinal data analysis.
4.4. Approximation of random effects in linear mixed models
In longitudinal data analysis, researchers are often interested in predicting the subject-specific trajectories of the response variable. To accomplish this prediction, the random effect for each subject needs to be approximated first. In linear mixed models, the conditional mean of
bi
can be predicted from data
y and
ˆβ
, given Equation
(4.26). In this section, I introduce a popular predictor in longitudinal data analysis, referred to as the best linear unbiased predictor (BLUP). Corresponding to the specification of BLUP, the shrinkage approach is also described, which is a powerful statistical technique in performing linear predictions of longitudinal trajectories.
4.4.1. Best linear unbiased prediction
BLUP was originally designed by
Henderson (1950, 1975) and now sees widespread applications in predicting the random effects in longitudinal data analysis. As indicated earlier, the fixed and the random components of the parameters can be estimated by the following two equations:
ˆβ=(∑Ni=1X′iV−1iXi)−1∑Ni=1X′iV−1iyi,
and
ˆbi=ˆGZ′iˆV−1i(yi−X′iˆβ).
In the second equation,
ˆbi
is computed as the proportion of the overall variance–covariance matrix that comes from the between-subjects variability times the overall residual from the marginal mean. Given this perspective, the covariance matrix of
ˆbi
as a parameter in a linear mixed model can be written as
var(ˆbi)=ˆGZ′i{ˆV−1i−ˆV−1iXi(∑Ni=1X′iˆV−1iXi)−1X′iˆV−1i}ZiˆG.
 (4.33)
(4.33)If
β,
G, and
R are known, the best linear predictor for
X′0β+Z′0b
, where
X0
and
Z0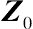
are matrices with some specific values, is
X′0β+Z′0GZ′V−1(y−X′ˆβ),
where
ˆβ
can be viewed as, in the general term, any solution for the following generalized least squares (GLS) equation
X′V−1X′ˆβ=X′V−1y.
As V is a large matrix containing G and R, Henderson (1950) specifies the celebrated BLUP equation, given by
(X′R−1X X′R−1Z Z′R−1XZ′R−1Z+G−1)(ˆβ ˆb)=(X′R−1y Z′R−1y).
 (4.36)
(4.36)For those not highly familiar with matrix algebra, the above block matrices can expand to the following simultaneous equations:
X′R−1X′ˆβ+X′R−1Zˆb=X′R−1y,
 (4.37a)
(4.37a)Z′R−1X′ˆβ+(Z′R−1Z+G−1)ˆb=Z′R−1y.
 (4.37b)
(4.37b)Henderson (1975) proves that in Equation
(4.36),
ˆβ
is a solution to Equation (4.35) and
ˆb
is equal to
GZ′V−1(y−X′ˆβ)
of Equation (4.34). The advantage of applying Equation
(4.36) over Equation (4.34) is that neither
V nor its inverse are required in the computation as
R is usually specified as an identify matrix and
G is often a diagonal matrix.
The variance–covariance matrix of parameter estimates in BLUP is also specified by
Henderson (1975), given by
E(ˆβ−β ˆb−b)(ˆβ−β ˆb−b)′=(X′R−1X X′R−1Z Z′R−1XZ′R−1Z+G−1)−1σ2.
 (4.38)
(4.38)In summary, the BLUP procedure maximizes the sum of two-component log-likelihoods given the joint distribution of
y and
b. In this expression, the log-likelihood is not a classical likelihood function in general linear models due to the specification of
b. Instead, BLUP selects estimates, or more accurately predictors, of
β,
b, and
σ2 to maximize the log-likelihood function. For the continuous response data, the BLUP estimators, denoted by
˜β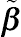
and
˜b
, are the values that make the derivatives of the log-likelihood function with respect to
β and
b equal
0 (
McGilchrist, 1994).
Statistically, the BLUP estimates have desirable distributional properties and may differ from those derived from the generalized least squares estimator. In the context of linear mixed models, BLUP estimates are linear in the sense that they are linear
functions of the data
y; unbiased because the average value of the estimate is equal to the average value of the quantity being estimated, written by
E(X′0β+Z′0b)=X′0β
; best in view of the fact that they have minimum mean squared error within the class of linear unbiased estimators; and prediction as to distinguish the estimates from the estimation of the fixed effects (
Henderson, 1975;
Robinson, 1991). For more details regarding BLUP’s derivations, justifications, and links to the other statistical techniques, the reader is referred to
Henderson (1950, 1975),
Liu et al. (2008),
McGilchrist (1994), and
Robinson (1991).
4.4.2. Shrinkage and reliability
Equations
(4.36) and
(4.38) imply that the estimation of model parameters depends on the relative size of the random effects per subject because
ˆbi
is equal to
GZ′iV−1i(yi−X′iˆβ)
. In the expression of
ˆbi
, the term
GZ′V−1
is the proportion of the overall covariance matrix that comes from the random effect components (
Verbeke and Molenberghs, 2000). Therefore, if between-subjects variability is relatively low, thereby indicating greater residuals, much weight will be given to the population predictor
X′ˆβ
. In contrast, if between-subjects variability is relatively high, much weight will be bestowed to the observed data
y. Consequently, the predicted outcome for subject
i, denoted by
ˆyi
, can be regarded as a weighted average of the model-based population mean and the observed data for subject
i. In statistics, this estimating technique is referred to as shrinkage, also called the borrowing of strength approach. In longitudinal data analysis, this technique not only plays an important role in the estimation of parameters in mixed-effects regression models, but it is also impactful in missing-data analysis and in the study on misspecification of the assumed distribution of predictions (
McCulloch and Neuhaus, 2011).
The concept of shrinkage might sound somewhat unfamiliar to the reader not highly familiar with advanced statistics. Given the importance of shrinkage in longitudinal data analysis, it may be useful to link shrinkage with the reliability analysis of the random effects applied in statistical inference of multilevel regression modeling (
Raudenbush and Bryk, 2002). The reliability of a measurement is defined as the ratio between the variance of true scores and the variance of observed data. In multilevel regression models, in which longitudinal data analysis can be regarded as a special case, reliability can be estimated by the ratio between the level-2 variance, denoted by
σ00
, and the sum of the level-2 and the level-1 variance components, with the latter divided by the number of observations within a level-2 unit
i. The equation is
ρ0i=σ00σ00+σ2/ni,
 (4.39)
(4.39)where
ρ0i
is the reliability score for level-2 unit
i,
σ2
is the level-1 variance, and
ni is the sample size within level-2 unit
i. Clearly, the smaller the size of
ni, the lower
the reliability for level-2 unit
i. Given Equation
(4.39), it is easy to calculate the reliability score of the random effects for each level-2 unit using the parameter estimates from a multilevel model.
The above reliability analysis can be extended to the longitudinal setting, in which the level-2 unit
i is the individual and the level-1 unit is a given observation at a given time point. In most datasets of a panel design, there are only a limited number of time points designed to follow up respondents at baseline, among whom many only have one, two, or three outcome observations due to various types of attrition (death, migration, or refusal to answer sensitive questions), as discussed in
Chapter 1. As a result, reliability is low for many subjects, thereby resulting in massive instability in the random-effects estimates. Given this long-existing problem in longitudinal data analysis, statisticians and other quantitative methodologists have applied the shrinkage approach to borrow information from subjects with high reliability in the estimation of the random effects for those with fewer observations (
Gelman et al., 2004;
Laird and Ware, 1982). In this empirical Bayes method, reliability of a subject is used as a weight factor in prediction of the random effects.
The shrinkage technique applied in longitudinal data analysis can be viewed as an extension of the above reliability analysis. From the inference described in
Section 4.4.1, the prediction of
y for subject
i can be specified by the following empirical Bayes algorithm:
ˆyi=X′iˆβ+Z′iˆbi=X′iˆβ+ZiˆGZ′iˆVi−1(yi−X′iˆβ)=(Ini−ZiˆGZ′iˆVi−1)X′iˆβ+ZiˆGZ′iˆVi−1yi=ˆRiVi−1X′iˆβ+(Ini−ˆRiˆVi−1)yi.
 (4.40)
(4.40)In the above BLUP estimation, prediction of the outcomes for subject
i is expressed as a weighted average of the population mean
X′iˆβ
and the observed data
yi, with weights
RiVi−1
and
Ini−RiΣi−1
, respectively. When within-subject variability is relatively sizable, the observed data are shrunk toward the prior average
X′iˆβ
because the weight component
Ini−RiΣi−1
is relatively low.
For the reader to better comprehend the rationale of the shrinkage approach in longitudinal data analysis, below I expand Equation
(4.40) to a random intercept linear model in which a scalar between-subjects random term,
bi, is specified. According to the inference described in
Section 4.4.1, the unbiased BLUP of
bi is given by
BLUP (ˆbi)=ˆσ2bˆσ2b+ˆσ2ɛ/ni(yi−X′iˆβ),
 (4.41)
(4.41)where the term
ˆσ2b/(ˆσ2b+ˆσ2ɛ/ni)
is referred to as the
shrinkage factor in longitudinal data analysis. By the inclusion of the shrinkage factor, the BLUP of
bi has mean 0 and variance
[ˆσ2b/(ˆσ2b+ˆσ2ɛ/ni)]ˆσ2b
. Therefore, the variance of
var|BLUP (ˆbi)|<var(bi)
.
It follows then that the BLUP of yi can be written as
ˆyi=X′iˆβ+ˆσ2bˆσ2b+ˆσ2ɛ/ni(yi−X′iˆβ).
 (4.42)
(4.42)After some algebra, Equation
(4.42) can be expanded to
BLUP (ˆyi)=yi−ˆσ2bˆσ2b+ˆσ2ɛ/ni(yi−X′iˆβ).
 (4.43)
(4.43)In the above random intercept model, the prediction of
yi depends on
σ2ɛ
,
σ2b
, and
ni
. Other things being equal, the number of observations for the subject determines the amount of shrinkage in linear estimation and prediction. In other words, if
ni
is small, within-subject variability is relatively large, and consequently, the observed data are more severely shrunk toward the population average
X′iˆβ
. This simple case can be readily extended to BLUP predictions in the linear random coefficient model.
In multilevel regression modeling, shrinkage has approved an efficient, robust, and consistent approach, even in the presence of large-scale missing observations. Its application in longitudinal data analysis, based on the MAR hypothesis, reduces instability in parameter estimates due to missing data and serial correlation among repeated measurements for the same subject.
Little and Rubin (1999) believe that in situations where good covariate information is available and included in the analysis, the MAR assumption is a reasonable approximation to reality. Given the application of shrinkage, the mixed-effects models have often been found to generate more reliable and robust outcomes than the models handling longitudinal data with the MNAR hypothesis. Furthermore,
McCulloch and Neuhaus (2011) found that very different distributions for BLUPs perform similarly in practice, as measured by mean square error; the random effects distributions that are statistically better fitting may not perform better in the overall prediction. Given such desirable properties, the standard approaches in linear mixed models, described in both
Chapter 3 and the present one, generally suffice to yield reliable parameter estimates and predictions. The statistical methods for handling exceptional cases of nonignorable missing data will be described and discussed in
Chapter 14.
In programming linear mixed models, many statistical software packages, including SAS, use various shrinkage estimators, combining empirical Bayes and the ML or the REML estimators for the estimation of parameters and prediction of the random effects. For example, in SAS, the PROC MIXED procedure provides the REML and BLUP estimators, both yielding Bayes-type shrinkage estimates (
SAS, 2012).
4.5. Hypothesis testing on variance component G
In performing hypothesis testing on the variance components in
G, the critical issue is whether the between-subjects variance components are tested on the boundary of the parameter space. If a hypothesis test is conducted on the non-negative variance of a single random effect,
σ2b˜i
, negative values are not allowed given the parameter space interval (0, ∞). In this situation, hypothesis testing should be performed on the boundary of the parameter space, and consequently, the classical hypothesis testing approaches are not valid. Instead, some one-sided testing statistics should be developed to test the null and the alternative hypotheses
H0:σ2b˜i=0
and
H1:σ2b˜i>0
(
Verbeke and Molenberghs, 2003). For large samples, the asymptotic null distribution of the likelihood ratio statistic should be approximated as a 50:50 mixture of two chi-square distributions (
Self and Liang, 1987).
For example, in the likelihood ratio test for the variance of a single random effect, the term
σ2b˜i
asymptotically follows a mixture of central chi-square distributions. In this case, the critical value should be set at
χ21,1−2α
, rather than
χ21,1−α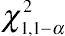
, for a significance test. Correspondingly, the adjusted
p-value of the likelihood ratio statistic is given by
p={1 if ˆΛ=00.5Pr(χ21≥ˆΛ) if ˆΛ>0} for q=1,
 (4.44)
(4.44)where
ˆΛ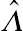
is the observed likelihood ratio test statistic. That is, for a single random effect, the
p-value of its variance is one-half of the
p-value for the regular
χ21
distribution.
If there are two random effect parameters under the null hypothesis, the p-value of the likelihood ratio statistic is written as
p=0.5Pr(χ21≥ˆΛ)+0.5Pr(χ22≥ˆΛ), for q=2.
 (4.45)
(4.45)Given the significance level α, the critical value, denoted by cα, for the likelihood ratio test can be obtained by the equation
α=0.5Pr(χ21≥c)+0.5Pr(χ22≥c).
 (4.46)
(4.46)For
q > 2, the researcher can test the statistical significance of the
qth element of the random effects
bi. Given the same rationale of the 50:50 mixture distributions, the
p-value of the likelihood ratio statistic, given as
ˆΛ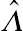
, is
p=0.5Pr(χ2s≥ˆΛ)+0.5Pr(χ2s+1≥ˆΛ), s=1, 2, ..., q−1.
 (4.47)
(4.47)In Equation
(4.47), the scenario is similar to the case for
q = 2 except that the first component on the right of Equation
(4.47) is a
q × 1 random vector. When
q is large, the above specified
p-value of the mixture distributions is closer to the classical likelihood ratio test statistic.
If a random effect is removed from an unstructured G matrix, the p-value of the likelihood ratio statistic is
p=0.5Pr(χ2˜q≥ˆΛ)+0.5Pr(χ2˜q−1≥ˆΛ).
 (4.48)
(4.48)In longitudinal data analysis, there are more complex situations for the specification of mixture distributions in the likelihood ratio test. In these complicated situations, it is not easy for the researcher to derive the mixing probabilities. One can use simulation techniques to calculate the
p-value. In this process, the structure of the information matrix and the approximating dimensions play important roles in the derivation of the asymptotic null distribution. For more details concerning the mixture distribution approach, the interested reader is referred to
Searle et al. (1992),
Self and Liang (1987); Verbeke and Molenberghs (
2000,
Chapter 6,
2003).
 .
. , referred to as a joint probability distribution and given by
, referred to as a joint probability distribution and given by (4.1)
(4.1) , is the Bayes expression of p(y), assuming ⌢θ
, is the Bayes expression of p(y), assuming ⌢θ (4.2)
(4.2) , which, as a function of ⌢θ
, which, as a function of ⌢θ , written as
, written as (4.4)
(4.4)
 (4.6)
(4.6) (4.7)
(4.7) (4.8)
(4.8) (4.9)
(4.9)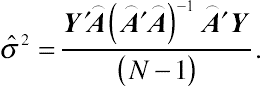 (4.10)
(4.10) (4.11)
(4.11) (4.12)
(4.12)
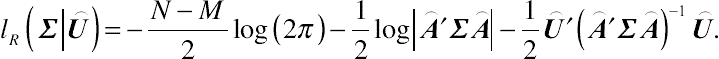 (4.13)
(4.13)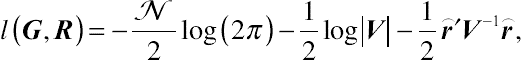 (4.14)
(4.14)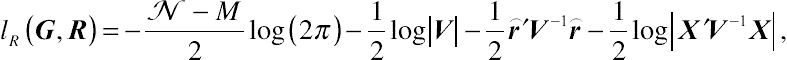 (4.15)
(4.15)

 (4.16)
(4.16)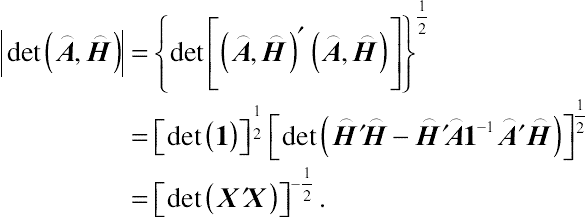 (4.19)
(4.19)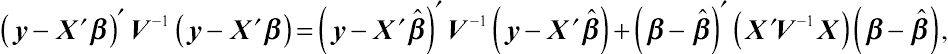
 (4.20)
(4.20) (4.22)
(4.22) (4.23)
(4.23) and r=y−X′β
and r=y−X′β (4.24)
(4.24) (4.25)
(4.25) (4.27)
(4.27) (4.28)
(4.28)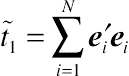 and ˜t2=∑Ni=1b′ibi
and ˜t2=∑Ni=1b′ibi , are the sufficient statistics for Ri and G, respectively.
, are the sufficient statistics for Ri and G, respectively. (4.29)
(4.29) (4.30)
(4.30)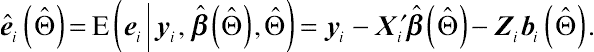
 (4.31)
(4.31) (4.32)
(4.32)
 (4.33)
(4.33) (4.36)
(4.36) of Equation (4.34). The advantage of applying Equation (4.36) over Equation (4.34) is that neither V nor its inverse are required in the computation as R is usually specified as an identify matrix and G is often a diagonal matrix.
of Equation (4.34). The advantage of applying Equation (4.36) over Equation (4.34) is that neither V nor its inverse are required in the computation as R is usually specified as an identify matrix and G is often a diagonal matrix. (4.38)
(4.38) . In the expression of ˆbi
. In the expression of ˆbi (4.39)
(4.39) (4.40)
(4.40) (4.41)
(4.41) .
. (4.42)
(4.42) (4.43)
(4.43) (4.44)
(4.44)