Appendix C
Quasi-likelihood functions and properties
The term quasi-likelihood function was initially introduced by Wedderburn (1974). While providing a way of allowing for overdispersion in statistical analysis, quasi-likelihood estimating equations are mostly applied for grouped binary or count data. In theories underlying this model, the quasi-likelihood function is shown to have similar properties to the log-likelihood function. Briefly, in this perspective, only relationship between the mean and the variance is specified in the form of a variance function.
Suppose we have independent observations Yi (i = 1, …, N) with expectation μi and variances V(μi), where V(·) is some known function. Let each observation μi be some known function of parameters β=(β1,...,βM)' . Then for each observation the quasi-likelihood function, denoted by Q(Yi,μi)
. Then for each observation the quasi-likelihood function, denoted by Q(Yi,μi) , is defined by the relation
, is defined by the relation
∂Q(Yi,μi)∂μi=Yi−μiV(μi),
 (C.1)
(C.1)or equivalently
∂∂μiQ(Yi,μi)=.∫μi Yi−μ′iV(μ′i)dμ′i+function of Yi.
For analytic convenience, the subscript i will be dropped in the succeeding texts, so that Y and μ will refer to an observation and its expectation, respectively.
Following immediately from the definition of Q , then Q
, then Q has the following first characteristic:
has the following first characteristic:
E(∂Q∂μ)=0.
 (C.2)
(C.2)By applying the chain rule, we have
∂Q∂βm=(∂Q∂μ)(∂μ∂βm),
where m = 1, …, M. Thus, we obtain another quasi-likelihood equation:
E(∂Q∂βm)=0.
 (C.3)
(C.3)Given V(μ) = var(Y), we have
E(∂Q ∂Q∂βm ∂βm′) =E(∂Q∂μ)2∂μ∂βm∂μ∂βm′=E{(Y−μ)2[V(μ)]2}∂μ∂βm∂μ∂βm′=1V(μ)∂μ∂βm∂μ∂βm′.
 (C.4)
(C.4)Also, the second partial derivative of the quasi-likelihood function with respect to β can be written by
−E(∂2Q ∂βm ∂βm′) =−E{∂∂βm′[Y−μV(μ)∂μ∂βm]}=−E{(Y−μ)∂∂βm′[1V(μ)∂μ∂βm]−1V(μ)∂μ∂βm∂μ∂βm′}=1V(μ)∂μ∂βm∂μ∂βm′.
 (C.5)
(C.5)Let l denote the log-likelihood and the distribution of Y be specified in terms of μ. Then, from the Cramér–Rao inequality (Stuart and Ord, 1994), we have
var(Y)≥−1E(∂2 l∂μ2).
 (C.6)
(C.6)Summarizing the above inferences, the quasi-likelihood Q has the following properties:
has the following properties:
Property (i):Property (ii):Property (iii):Property (iv):Property (v):E(∂Q∂μ)=0,E(∂Q∂βm)=0,E(∂Q∂μ)2=−E(∂2Q∂μ2)=1V(μ),E(∂Q ∂Q∂βm ∂βm′)=−E(∂2Q ∂βm ∂βm′)=1V(μ)∂μ∂βm∂μ∂βm′,−E(∂2Q∂μ2)≤−E(∂2 l∂μ2),

where Property (iii) is a special case of (iv), and for a one-parameter exponential family, the inequality in Property (v) becomes equality.
Wedderburn (1974) mathematically proves that the precision of maximum quasi-likelihood estimates can be
estimated from the expected second derivatives of
Q
in the same fashion as the precision of maximum likelihood estimates is estimated from the expected second derivatives of the log likelihood. In practice, using the Newton–Raphson method with the expected second derivatives of
Q
to calculate
βˆ
is equivalent to iteratively calculating a weighted linear regression of the residuals on the quantities of the scores by linear least squares, with the residuals and the score being calculated from the current estimate of
βˆ
.
![]() . Then for each observation the quasi-likelihood function, denoted by
. Then for each observation the quasi-likelihood function, denoted by ![]() , is defined by the relation
, is defined by the relation (C.1)
(C.1)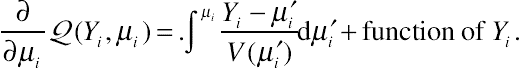
![]() , then
, then ![]() has the following first characteristic:
has the following first characteristic: (C.2)
(C.2)
 (C.3)
(C.3) (C.4)
(C.4) (C.5)
(C.5) (C.6)
(C.6)![]() has the following properties:
has the following properties:
