In longitudinal analysis on categorical outcome data, the analytic focus for the majority of empirical studies is placed upon individual-based or population-averaged trajectories of the response outcomes, as associated with certain covariates of interest. Occasionally, researchers seek to link such longitudinal trajectories to a prior status for predicting transition probabilities from a state of origin to a set of destination states. Such transition analyses are particularly popular in demographic and epidemiological studies, providing important information with policy implications to planners, policymakers, and academics. In medical research, transition analysis has tremendous promises, particularly since clinicians are usually interested more in the efficacy of a new medication or medical treatment on recovery from a medical condition than in the pattern of change over time in a disease’s prevalence. In the literature of multistate transitions, the Markov chain, fixed-effects techniques have been applied in various disciplines. In the analysis of longitudinal data with more than two time points, these classical approaches do not have sufficient capabilities for handling intraindividual correlation and unobserved heterogeneity. Mixed-effects regression modeling is perhaps the most appropriate statistical perspective for the analysis of multidimensional transitions.
In this chapter, a number of multidimensional transition models are described, which link categorical outcome data to time, value of a prior state, and other theoretically relevant covariates. I first review the classical approaches designed to model multidimensional transitions between only two time points. Next, I delineate some simple Markov chain regression models in the analysis of multidimensional transitions across more than two time points, using the fixed-effects perspective. The strengths and limitations of those fixed-effects techniques are discussed. The mixed-effects multinomial logit transition model is then introduced, with the description including model specifications, statistical inference, nonlinear predictions, and the approximation of the variance–covariance matrix for the predicted transition probabilities. Lastly, I provide an empirical illustration for the application of the mixed-effects multinomial logit transition model. All the multidimensional transition models described in this chapter build upon a competing risks framework, and therefore, the transition models for Gaussian or binary outcome data are not included in this text.
12.1. Overview of two-time multinomial transition modeling
Transition models were primarily developed and applied in the fields of demography, aging and health, and epidemiology. Given the lack of longitudinal data in the past, the classical transition models were mostly created for generalizing transition patterns between only two time points, the baseline and the follow-up, in the format of the multistate life table. Examples of such two-time transition models include transitions in multiple modes of health (
Crimmins et al., 1994), labor force participation (
Hayward and Grady, 1990), flows of migration from one geographical region to another (
Willekens and Rogers, 1978), and multidimensional transitions in health care (
Liu et al., 1997). Those models generally specified two or more states of origin (the state at the beginning of a specified observation interval) and three or more states at destination (the state at the end of the observation interval), which, combined, constitute a finite state space for a set of stochastic, multidimensional, and one-step transition processes. As heterogeneity is always intrinsic in longitudinal transitions, some researchers employed a multivariate approach for creating a two-time transition model. For example, some scientists used the hazard rate or the logistic regression model in the analysis of multidimensional transitions (
Gill, 1992;
Hayward and Grady, 1990;
Land et al., 1994). Given the desirable large sample property, those approaches are appropriate for handling substantial population heterogeneity in generalizing stochastic processes of two-time transitions and have the added advantage of deriving group-based estimates from data with a small sample size (
Land et al., 1994).
Liu et al. (1995) developed a competing-risks multinomial logit model on transitions in functional status in an older Japanese population, using a number of
theoretically relevant covariates as predictors on transitions. Given the data available only at two time points in that period, this multidimensional regression model consisted of six possible transitions, defined as the change in functional status between the baseline and follow-up investigations. At the beginning of the time interval, individuals are divided into two groups according to functional status, functional independence, and functional dependence, denoted by
Y0 = 0, 1. At the end of the observation interval, there are three possible outcomes with respect to an individual’s functional status, including functional independence, functional dependence, and deceased during the interval, respectively, denoted by
Y1 = 1, 2, 3. Consequently, there are six possible transition types given two functional states at baseline and three possible states at destination. Between the two functional states, functional independence and functional dependence, a transition can occur from either direction within the time interval, and therefore, they are called the transient states. The third status at destination, dead, is a permanently ending state, thereby referred to as the absorbing state. I let
i˜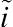 (i˜=0,1)
(i˜=0,1)
stand for the origin state and
k (
k = 1, 2, 3) denote the destination state.
There are two ways to model functional status transitions using the multinomial logit regression. If the sample size is reasonably large for each status group at baseline, a nested multinomial logit model can be specified on competing outcomes, using the functional status at baseline (presence vs. absence of disability) as a predictor in the model. The effect of the baseline state on the association between another covariate and the outcome states can be specified by creating an interaction term between the baseline functional status and that covariate. Let
Yi1 denote the value of a multinomial variable, indicating functional status at follow-up for subject
i. It follows then that the transition probability that
Yi1 =
k (
k = 1, …,
K) for subject
i given prior state
Yi0=i˜ (i˜=0, 1)
is given by
π˜i1k=Pr(Yi1=k|Yi0,Xi0)=[1+∑Kl=1exp(Yi0β1l+X′i0βrl)]−1exp(Yi0β1k+X′i0βrk), for Yi0 = 0, 1,
 (12.1)
(12.1)where
π˜i1k
represents the transition probability from functional status at baseline
i˜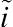
to destination state
k between time 0 and time 1, and
Xi0
is the
M × 1 vector of the covariates other than
Yi0, which, measured at baseline, may include one or more interaction terms. Likewise,
β1k
is the regression coefficient of functional status at baseline, and
βrk
is the
M × 1 vector of unknown regression parameters for other covariates on outcome state
k. The probability
π˜i1(K+1)
is specified as the residual probability, as in a regular multinomial logit regression.
By functional transformation, a typical multinomial logit transition model given prior state Yi0 and other covariates Xi can be expressed as a generalized linear model, given by
Log(π˜i1kπ˜i1(K+1))=Yi0β1k+X′i0βrk, i˜=0,1; k=1,...,K,
 (12.2a)
(12.2a)or
log it Pr(Yi1=k∣∣Yi0=i˜,Xi0)=Yi0β1k+X′i0βrk=ηi1k.
 (12.2b)
(12.2b)If there are a large number of covariates considered in a unified transition model with effects depending significantly on health state at baseline, the specification of too many interaction terms can cause strong numeric instability and a lack of statistical efficiency in estimating the multinomial logit parameters (
Liu et al., 1995). In such situations, an alternative approach is to model the competing risks of the multinomial response separately for each state at baseline. That is, the estimation of model parameters consists of two separate regression models, with each associated with an independent estimating process, given by
log it Pr(Yi1=k|Yi0=0,Xi0)=X′i0β0k,
 (12.3a)
(12.3a)log it Pr(Yi1=k|Yi0=1,Xi0)=X′i0β1k,
 (12.3b)
(12.3b)where the coefficient vector
βk
is subscripted by 0 or 1, and therefore, a unique set of coefficients is specified in association with a specific state of origin. This specification allows the effects of covariates on each logit component to differ between the two states of origin, and consequently, the specification of extra interaction terms is avoided.
The above two multinomial logit perspectives for prediction of the transition probabilities have their respective strengths and limitations. The unified multinomial logit regression model is fitted by maximizing the entire likelihood function over all parameters in an integrated estimating process. If the sample size is sufficiently large, this approach is statistically more efficient than the other. The application of this approach, however, does not function well when there are too many interaction terms specified in the model. The transition model specifying separate maximization processes is a robust alternative when the unifying approach fails to yield statistically stable and consistent regression coefficient estimates. From the statistical standpoint, however, this second statistical approach is not highly efficient because it is hard to statistically evaluate differences in parameter estimates with different sample sizes for the baseline groups. Using both perspectives in an empirical study can help the researcher command a better understanding of a covariate’s effects on a set of competing risks.
The model parameters in the multinomial logit transition model can be estimated by applying the standard procedures for the classical multinomial logit modeling. As the procedure is described extensively in
Section 11.1, the detailed steps are not further elaborated in this section. The variance–covariance matrix for the predicted transition probabilities, needed to evaluate the quality of nonlinear predictions, can be obtained from the delta method by extending the approach described in
Chapter 11. Suppose that
Lˆi˜k
is a random vector of the predicted multinomial logit components for transitions from baseline state
i˜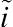
to destination state
k (Lˆi˜k=Lˆi˜1,....,Lˆi˜K)
with mean
ηi˜k
and the variance–covariance matrix
Vˆ(Lˆi˜k)
,
and
Π˜ˆi˜k=g−1(Lˆi˜k)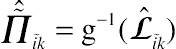
is a transform of
Lˆi˜k
where
g−1
is the inverse link function. The first-order Taylor series expansion of
g(Lˆi˜k)
yields approximation of mean
E[g(Lˆi˜k)]≈g(ηi˜k),
 (12.4)
(12.4)and the variance–covariance matrix
Vˆ(Π˜ˆi˜k)
V[g(Lˆi˜k)]≈[∂ g(Lˆi˜k)∂ Lˆi˜k∣∣Lˆi˜k=ηi˜k]′V(Lˆi˜k)[∂g(Lˆi˜k)∂Lˆi˜k∣∣Lˆi˜k=ηi˜k].
 (12.5)
(12.5)For the reader interested in this approach of approximation, a detailed description of the delta method is provided in
Appendix B.
Given Equation
(12.5), the variance–covariance matrix for a given set of the predicted transition probabilities can be approximated, based on which other measurements for the construction of a multistate life table can be estimated (
Liu et al., 1995). Because a set of the transition probabilities must sum to unity, all the transition probabilities originating from a specific baseline state should be regarded as statistically meaningful if any one of them is statistically significant (
Liu et al., 1995).
Because an actual transition probability is not empirically observable for an individual, the logit function does not have an observed value, and therefore, the variance–covariance matrix for the predicted logit components is not directly obtainable from empirical data. For this hindrance, the statistical method described in
Chapter 11 is recommended to obtain an approximate of the variance–covariance matrix for the logit components. Specifically, the score function, the first partial derivative of the log-likelihoods, approximates the residuals for a mean multinomial function conditionally on the model parameters. Consequently, the variances/covariance matrix of the random errors on the predicted logit components can be approximated by the local subset of the intercepts in the inverse of the observed Fisher information matrix. As indicated in
Chapter 11, in this approximation the covariates need to be rescaled to be centered at selected values.
In health research, a distinctive advantage of using the multinomial logit model is its capability to yield approximates of the variance–covariance matrix for the multinomial response data. The data structure of the multinomial response is multivariate, rather than univariate, given the constraint that a set of the transition probabilities must sum up to unity. With this constraint, in the construct of the multinomial logit model even the sets of regression coefficients on the logit components are correlated (
Greene, 2003). The specification of separate binary logistic regression models on the multinomial response data only can yield the univariate variances for the predicted transition probabilities, thereby resulting in bias in the standard error estimates. Perhaps due to such concerns, since the publication of the original article applying the multinomial logit model (
Liu et al., 1995) the multinomial logit approach has become increasingly popular in the analysis of multidimensional transitions in health studies. For example, the method has been replicated by
Zimmer et al. (1998), extended to the framework of structural equation modeling (
Liang et al., 2001;
Liu et al., 2006),
and used in a competing risks analysis on transitions in multiple idiopathic physical symptoms (
Engel et al., 2002).
Lièvre et al. (2003) developed a similar multinomial logit approach for estimating the transition probabilities and the health expectancies given the Markov chain assumption, though without the specification of the model covariates other than the time factor. The validity of the embedded Markov chain hypothesis in longitudinal data analysis will be discussed in
Section 12.3.
12.2. Longitudinal transition models with only fixed effects
In the two-time health transition model, statistical inference and the resulting estimating procedures essentially rely on a cross-sectional data structure with the baseline health status used either as a covariate or as defining a subsample of the analysis. Given only one data point for each individual, strictly speaking the two-time multinomial logit transition model is not in the domain of longitudinal data analysis. When more than two time points are specified, the data structure becomes more complex because a subject has at least two data points (in the data matrix, each subject has more than one row). The resulting dependence in this data structure thereby calls for the development of more advanced techniques to account for intraindividual correlation.
With a sequence of observed time points for subject i, the conditional distribution of the multinomial response at the jth time point, denoted by Yij where j = 1, …, ni, can be viewed as a function of the prior response or responses and covariates Xij. The simplest longitudinal transition model for data with more than two time points follows the basic Markov chain hypothesis that longitudinal transitions between different values in the state space depend only on the value of the previous state. Correspondingly, the transition probability from the state at time point j − 1 to the state at time point j can be written as a Markov process, given by
π˜ijk=Pr(Yi1=k∣∣Yi(j−1)=i˜), for i˜=0, 1; k=1,...,K+1,
 (12.6)
(12.6)where prior state
Yi(j−1)
and current state
Yij
are subject to different state spaces because the prior state space does not include an absorbing state but
Yij
does. With the specification of the Markov random variable, the only information about the past for predicting the present is the previous state. This basic Markov hypothesis implies that knowledge of the state values at times earlier than
j − 1 do not change the transition probability between
j − 1 and
j, thereby being overlooked. If such a Markov process is correctly assumed, it is reasonable to specify a separate multinomial logit model for each prior state value on
K outcome values.
Let
Yi(j−1)=0, 1
and
Yij=1,...,K+1
. Two separate multinomial logit models, with covariate vector
Xij
, can then be specified for
Yi(j−1)=0
and
Yi(j−1)=1
, respectively, written as
log it Pr(Yij=k∣∣Yi(j−1)=0,Xij)=X′ijβ0k,
 (12.7a)
(12.7a)log it Pr(Yij=k∣∣Yi(j−1)=1,Xij)=X′ijβ1k,
 (12.7b)
(12.7b)where, given subscript 0 or 1,
β0k
and
β1k
may differ to allow for variations in the effects of
Xij
between the two prior states.
As indicated in the description of the two-time transition model, the application of separate transition models can yield statistically inefficient results on parameter estimates and the corresponding standard errors. If serious problems arise, an integrated multinomial logit transition model can be specified by using the prior state as a covariate, given by
log it Pr(Yij=k∣∣Yi(j−1)=i˜,Xij)=Yi(j−1)β1k+X′ijβ0k,
 (12.8)
(12.8)where
β1k
, in the context of a longitudinal transition model, is the regression coefficient of the prior state at time
j − 1. With
Yi(j−1)
taking value 0 or 1,
β1k=β0k+β1k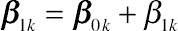
. Some interaction terms may be specified in
β0k
to account for differences in the effects of certain covariates between the two prior status groups. As only the immediately previous state is considered in predicting the logit on the current state, the above two types of transition models, separate or unified, are referred to as the first-order Markov chain models (
Diggle et al., 2002). This first-order Markov chain approach is somewhat popular in the analysis of health transitions and life expectancies (e.g.,
Lièvre et al., 2003). Ignoring intraindividual correlation in analyzing health transitions, conditionally on prior state, can result in substantial bias in nonlinear predictions of the transition probabilities.
Some researchers extend the above-mentioned first-order Markov approach by specifying a full set of the past responses, denoted by
Hij
, to create a transition model (
Diggle et al., 2002). Mathematically,
Hij
can be defined as the σ-algebra of the prior history of transitions, given by
Hij=σ{Yi(j−1),...,Yi(j−q˜)}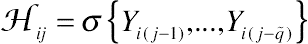
, where
q˜
is the number of prior observations. With the specification of
Hij
, the multinomial logit of the Markov chain
(Yij|Hij,Xij)=k(k=1,...,K)
for subject
i at time point
j can be written as
log it Pr(Yij=k|Hij,Xij)=∑q˜r˜=1Yi(j−r˜)βr˜k+X′ijβq˜k,
 (12.9)
(12.9)where
βr˜k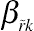
is the regression coefficient of the state value at time point
(j−r˜)
. The vector of regression coefficients for
Xij
given
Hij
, denoted by
βq˜k
, indicates that the value and the interpretation of the regression coefficients change with the Markov order
q˜
. Theoretically, when the above Markov model is correctly assumed, the transition events are conditionally uncorrelated, and consequently, the classical multinomial logit model with only fixed effects can be applied to estimate the regression coefficients and the corresponding standard errors (
Diggle et al., 2002). When too many time points are considered, the value of
q˜
is high, thereby making the estimating process tedious and cumbersome. The regression becomes even denser when the order of prior states impacts the effects of the covariates on the
response at the current time point. Specification of a large number of interaction terms will further complicate estimation of the parameters, thereby affecting the precision of the estimates. Furthermore, the precision in the parameter estimates depends on the Markov order in
Hij
; that is, for earlier responses, the information of the past responses is limited to fewer previous time occasions, and only for the last observed time point, the specified set of the past responses is complete. As a result, data at early times tend to be more correlated than the measurements of the response at later points.
As previously indicated, with dependence among repeated measurements of the response for the same subject, the specification of the between-subjects random effects is statistically efficient and effective to account for intraindividual correlation inherent in longitudinal data. Correspondingly, a heterogeneous transition pattern can be assumed to address the association between the history of transition events and the current state, conditionally on the specified fixed and random parameters. The mixed-effects multinomial logit model described in
Chapter 11 can be extended to the perspective of multidimensional transitions from prior state to a set of competing destination states. With the inclusion of the prior state as a covariate and the specification of the subject-specific random effects, the transition probabilities can be adequately predicted.
12.3. Mixed-effects multinomial logit transition models
The mixed-effects multinomial logit transition model is an extension of the mixed-effects multinomial logit perspective described in
Chapter 11 by adding a prior state variable to the covariate vector in model specifications and statistical inference. In the description of this approach, I start with the random intercept multinomial logit transition model, followed by a brief introduction of the random coefficient multinomial logit transition model. Next, I delineate statistical inference of the mixed-effects multinomial logit transition model, the approximation procedure of the variance–covariance matrix for the predicted transition probabilities, and the construction of separate multinomial logit transition models in some special situations.
12.3.1. Random intercept multinomial logit transition model
Let
Yijk denote the value of a categorical outcome variable with
K + 1 levels associated with subject
i at time point
j where
j = 1, …,
ni. For illustrative simplicity and analytic convenience, I begin with the random intercept multinomial logit model with adding a covariate representing prior state at time point
j − 1, denoted by
Yi(j−1).
Using
Yij = (
K + 1) as the reference, the transition probability that
Yij =
k (
k = 1, …,
K), given prior state
Yi(j−1)
and covariate vector
Xij
, is given by
π˜ijk=Pr(Yij=k∣∣Yi(j−1),Xij,bik) =[1+∑Kl=1exp(Yi(j−1)β1l+X′ijβrl+bil+ɛijl)]−1exp(Yi(j−1)β1k+X′ijβrk+bik+ɛijk) =[1+∑Kl=1exp(Yi(j−1)β1l+X′ijβrl)exp(bil+ɛijl)]−1exp(Yi(j−1)β1k+X′ijβrk)exp(bik+ɛijk), for j=1,...,ni,
 (12.10)
(12.10)where
Xij
consists of the covariates other than
Yi(j−1), including the time factor, specified for modeling longitudinal, multidimensional transitions,
β1k
is the regression coefficient of
Yi(j−1) on destination state
k, and
βrk
is the
M × 1 vector of unknown regression parameters of
Xij
. With respect to the random terms,
bik
is the between-subjects random effect assumed to be distributed as
N(0,σ2bk)
, and
ɛijk
is the within-subject random error distributed as
N(0,σ2ɛijk)
. As defined, the transition probability
π˜ij(K+1)
is the reference probability. Notice that while the time factor must be measured at time point
j, the other covariates contained in
Xij
need to be measured at time point (
j − 1). The development of this multivariate transition model is based on the analytic strategy that
Yi(j−1) is used as a covariate for linking the multinomial response at time point
j to the prior state at time point
j − 1, with the impact of the prior transition history before
j − 1 being accounted for by the specified random effects.
As in the mixed-effects multinomial logit model, Equation
(12.10) can be transformed into a combination of linear specifications for
K log odds. With the (
K + 1)th level serving as the reference, the inverse of Equation
(12.10) for level
k generates a typical random intercept multinomial logit transition model, given by
log(π˜ijkπ˜ij(K+1))=logit Pr(Yij=k∣∣Yi(j−1),Xijbik) =Yi(j−1)β1k+X′ijβrk+bik+ɛijk, where k=1,...,K.
 (12.11)
(12.11)As discussed on several occasions in the preceding chapters, the inherent within-subject variability cannot be directly captured in the observed multinomial response because an individual’s probability is not empirically observable at a specific time point. Ignoring the presence of the within-subject random errors, however, can result in substantial retransformation bias in nonlinear predictions of the transition probabilities. The within-subject random errors, if specified, can be approximated by using the score equation with the covariates rescaled to be centered at certain selected values, denoted by
X0. Given the application of centering on covariates, the logit
intercepts correspond to a mean multinomial logit function with respect to
X0. For example, let time
T be centered at five,
Yi(j−1)
is 0 or 1, and the other covariates be rescaled to be centered at sample means at time point
j − 1. It follows that the intercepts in the multinomial logit transition model correspond to the mean logits with respect to transitions from the prior state of value 0 to
K destination states at time point
j for a typical individual at time five. As a result, the score function approximates the within-subject random errors corresponding to the mean multinomial components conditionally on the between-subjects random effects and other specified parameters. The variance–covariance matrix of within-subjects random errors in the random intercept multinomial logit transition model can be approximated by using the local subset of the intercepts in the variance–covariance matrix for the fixed effects on the logit components.
Given the approximate of
σ2ɛk
, the transition probability from a given prior state at time point
j − 1 to the destination state
k at time point
j can be predicted by retransforming the linear predictor in Equation
(12.10). The predicting formula is
π˜ˆijk=Pr(Yij=k∣∣Yi(j−1),Xij,bˆik,ɛˆijk) =[1+∑Kl=1exp(Yi(j−1)βˆ1l+X′ijβˆrl)Φˆijl]−1exp(Yi(j−1)βˆ1k+X′ijβˆrk)Φˆijk, for k=1,...,K;l=1,...,K,
 (12.12)
(12.12)where
Φˆijk=exp[(bˆik+ɛˆijk)∣∣Yi(j−1)]
is the estimated multiplicative random error variable for subject
i on destination state
k (
k = 1, …,
K) given prior state
Yi(j−1)
. Given the prior distribution of the random components on transition probability
π˜ˆijk
being lognormal, the expectation of
Φˆijk
is given by
E(Φijk∣∣Yi(j−1),bik)=exp[(σ2bik+σ2ɛijk)∣∣Yi(j−1)2],
with variance
var(Φijk∣∣Yi(j−1),bik)=exp{2[(σ2bik+σ2ɛijk)∣∣Yi(j−1)]}−exp[(σ2bik+σ2ɛijk)∣∣Yi(j−1)].

Analogous to the corresponding equation in
Chapter 11, Equation
(12.12) is defined as the inverse link function of the random intercept multinomial logit transition model, with the random components parameterized by two variance terms to correct retransformation bias in nonlinear predictions. With positive skewness of the posterior predictive distribution, the expectation of
Φijk∣∣Yi(j−1),bik
is greater than unity, with equality holding if and only if
σ2bik∣∣Yi(j−1)=σ2ɛijk∣∣Yi(j−1)=0
. Conditionally on
βk
and
Yi(j−1)
, the vector of variances for the between-subjects and the within-subject
random components for
K levels, written as
V(O∣∣Yi(j−1))
and
V(E∣∣Yi(j−1))
, contain values
{σ2bi1∣∣Yi(j−1),...,σ2biK∣∣Yi(j−1)}′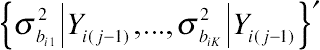
and
{σ2ɛij1∣∣Yi(j−1),...,σ2ɛijK∣∣Yi(j−1)}′
, respectively, with the latter specified as local approximations that vary over time points. Therefore, this random intercept multinomial logit transition model does not yield a CS pattern in the joint variance–covariance matrix for the predicted transition probabilities unless intrasubject correlation is zero for all subjects with the inclusion of prior state as a covariate. The relative size of
{σ2bi1∣∣Yi(j−1),...,σ2biK∣∣Yi(j−1)}′
determines whether the within-subject random errors can be ignored in predicting the transition probabilities for
K + 1 response levels longitudinally.
At first glance, Equation
(12.12) seemingly specifies a Markov chain process as the response at time point
j looks only related to prior state
Yi(j−1)
. With the specification of the time-dependent covariates and the between-subjects random effects, however, the equation actually specifies a semi-Markov transition process in which the current response is not only associated with the immediately prior response but also affected by both the observed and the unobserved heterogeneous factors. In particular, the specified random effects implicitly carry information of the influences from unspecified, unrecognizable factors, thereby accounting for the remaining elements of intraindividual correlation conditionally on the effect of prior state.
If
(Φˆijk∣∣Yi(j−1))
and
Xij
are replaced with
E(Φijk∣∣Yi(j−1))
and
X0, respectively, Equation
(12.12) predicts the marginal transition probabilities from the origin state
Yi(j−1)
to
K + 1 destination states at time point
j for a population taking covariate values
X0. The individual transition probabilities within the population are randomly scattered around each marginalized probability following the assumed prior distributions of both the between-subjects random effects and within-subject random errors. Because the expected value of the random variable
(Φˆijk∣∣Yi(j−1))
is greater than unity, overlooking retransformation of the random components in predicting a set of transition probabilities can result in serious retransformation bias in the predictions.
12.3.2. Random coefficient multinomial logit transition model
When the effects of some covariates on longitudinal transitions are considered to vary significantly over individuals, the random coefficient multinomial logit transition model needs to be specified and empirically applied. By replacing the term
bik
in Equation
(12.11) with
Z′ijbik
, the mixed-effects multinomial logit transition model is given by
logit Pr(Yij=k∣∣Yi(j−1),Xij,bik) =Yi(j−1)β1k+X′ijβrk+Z′ijbik+ɛijk, where k=1,...,K,
 (12.13)
(12.13)where
bik={bi1,...,biq}′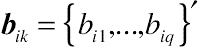
is a
q × 1 vector of unknown individual-specific random effects for outcome level
k, and
Zij is a design matrix for
bik. Analogous to
the corresponding specification in
Chapter 11, it is assumed that E(
bik ∣∣Yi(j−1)
) =
0, cov(
bik ∣∣Yi(j−1)
) =
Gk ∣∣Yi(j−1)
, and cov(
bik,
ɛijk ∣∣Yi(j−1)
) =
0. As defined, the multiplicative random variable for subject
i on response level
k (
k = 1, …,
K) follows a lognormal distribution. Given the value of prior state
Yi(j−1)
, the posterior predictive distribution of the random variable
(Φijk∣∣Yi(j−1),bik)
has mean
E(Φijk∣∣Yi(j−1),bik)=exp[Zij(Gk∣∣Yi(j−1))Z′ij+σ2ɛijk∣∣Yi(j−1)2],
 (12.14)
(12.14)and variance
var(Φijk∣∣Yi(j−1),bik)=exp{2[Zij(Gk∣∣Yi(j−1))Z′ij+σ2ɛijk∣∣Yi(j−1)]} −exp[Zij(Gk∣∣Yi(j−1))Z′ij+σ2ɛijk∣∣Yi(j−1)].
 (12.15)
(12.15)With the above specifications, the random intercept multinomial logit transition model can be regarded as a special case of the random coefficient multinomial logit transition model, with
Zij and
bik each containing only one element. If the random term, either the random intercept or the random coefficient, is correctly specified,
π˜ˆijk
provides an unbiased approximate of the transition probability from prior state
Yi(j−1)
to destination state
k at time point
j, behaving as a function of covariate vector
Xij and the past responses
Yi(j−1),...,Yi(j−q˜)
by means of the specified random effects.
As noted in
Chapter 11, the application of a random coefficient multinomial logit regression considerably complicates statistical inference and the estimating process given a longitudinal, multivariate distribution of the multidimensional responses. Therefore, some caution must be exercised when applying this complex transition model, particularly when the model complicates state-to-state transition processes. Specifically, in the estimation of a random coefficient transition model, the variance–covariance structure will expand to a block covariance matrix, and consequently, numeric instability often arises in the estimating process. Although the random intercept regression model specifies a CS covariance structure for the between-subjects random effects, it makes the joint random variable time-dependent to use local approximations for within-subjects random errors. Therefore, the inclusion of a within-subject error term captures a portion of variations in the effects of covariates. Empirically, specification of both variance components as time-varying is often unnecessary.
12.3.3. Statistical inference of mixed-effects multinomial logit transition model
Let
θ be the vector of parameters with elements
β and
V(O)
in the mixed-effects multinomial logit transition model where
β includes the regression coefficients of the prior state variable on
K log odds. It follows that, for subject
i, the likelihood function
in the mixed-effects multinomial logit transition model, given as
θ, can be written as a joint probability:
L(Yi∣∣Yi(j−1),θ)=∏nij=2∏K+1k=1(π˜ijk∣∣Yi(j−1))Yijk∣∣Yi(j−1),
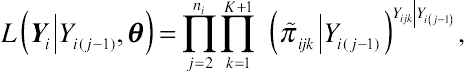 (12.16)
(12.16)where
Yijk∣∣Yi(j−1)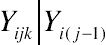
is 1 if the
ith subject falls in response level
k at time point
j and is 0 if otherwise given prior state
Yi(j−1)
, and
Yi is the (
ni −1) × (
K + 1) response matrix conditionally on prior state
Yi(j−1)
. With the specification of the prior state variable
Yi(j−1)
,
j is specified as
j = 2, …,
ni in the joint likelihood. For
k = 1, …,
K,
π˜ijk∣∣Yi(j−1)
is specified by Equation
(12.10) or Equation
(12.13), depending on the specification of the between-subjects random effects. As the reference probability, the estimation of
π˜K+1∣∣Yi(j−1)
relies on the estimates of nonreference transition probabilities in the same set, given by
π˜ˆK+1∣∣Yi(j−1)=1−π˜ˆ1∣∣Yi(j−1)−...−π˜ˆK∣∣Yi(j−1)
.
Taking log values on both sides of Equation
(12.16) gives rise to
l(Yi∣∣Yi(j−1),θ)=∑nij=2∑K+1k=1Yijk∣∣Yi(j−1)log(π˜ijk∣∣Yi(j−1)).
 (12.17)
(12.17)Following the procedure described in
Section 11.3, maximizing the above log-likelihood function over all individuals yields statistically efficient and robust estimates of
β and the random term
V(O)
. With including the fixed effects of prior state
Yi(j−1)
and the between-subjects random effects in
θ, statistically efficient and robust estimates of the model parameters on the multinomial response data can be obtained. Nonlinear predictions of the transition probabilities can be performed by using one of the approximation methods described in
Chapter 8. With the transition analysis generally being focused on the pattern for a population of interest, rather than on individuals, the marginal transition probabilities should be specified and predicted.
Let g be the logit link function and g
−1 be its inverse function. Then, the expectation of the transition probability
π˜ijk
can be expressed as
E(π˜ijk∣∣Yi(j−1),θ)=∫g−1[Yi(j−1)β1k+X′ijβrk+log(Φijk∣∣Yi(j−1))] dF (Φij∣∣Yi(j−1)),
 (12.18)
(12.18)where the error distributional function
F is the cumulative density function, and
Φij∣∣Yi(j−1)
is a vector of multiplicative random variables containing elements
{Φij1∣∣Yi(j−1),...,ΦijK∣∣Yi(j−1)}′
. Analogous to the description in
Chapter 11, the differential term is written as
dF(Φij∣∣Yi(j−1))
instead of
dF(Φijk∣∣Yi(j−1))
because nonlinear prediction of the transition probability
π˜ijk
involves all logit components. Conditionally on prior state
Yi(j−1)
,
β, and
Φij
, within-subjects random errors are embedded in the fixed effects in multinomial logit regression modeling (
Amemiya, 1985;
Zeger et al., 1988), with the variance–covariance matrix of random errors denoted by
V(e∣∣Yi(j−1))
.
I would like to alert the reader that in the analysis of longitudinal data with more than two observed time points, the estimator
g−1(Yi(j−1)β1k+X′ijβˆk)
does not predict the marginal mean of
π˜ijk
unless there is strong evidence that the first-order Markov
chain hypothesis is valid. Because
F is not a cumulative normal function,
π˜ˆijk
is usually not
g−1(Yi(j−1)β1k+X′ijβˆk)
, and therefore, retransformation of the random components is usually indispensable in predicting the transition probabilities.
Let N be the total number of subjects. The maximum likelihood estimates of θ in the random-effects multinomial logit transition model can be obtained by solving the following equation:
∂ l∂ θ=∑Ni=1g−1(Yi∣∣Yi(j−1))[∂ g(Yi∣∣Yi(j−1))∂ θ]=0.
 (12.19)
(12.19)As defined, the first partial derivative of the log-likelihood is the score function, used as approximates of the within-subject random errors.
The Fisher information matrix, the negative of the expected second partial derivative of the log-likelihood and denoted by
I(θ)
, is given by
I(θ)=E(−∂2 l∂ θ∂ θ′∣∣Yi(j−1))=∑Ni=1g−2(Yi)∂ g(Yi∣∣Yi(j−1))∂ θ[∂ g(Yi∣∣Yi(j−1))∂ θ]′.
 (12.20)
(12.20)As indicated in
Chapter 11, the inverse of the observed information matrix approximates the variance–covariance matrix for parameter estimates in the mixed-effects multinomial logit model. With prior state specified as a predictor, Equation
(12.20) can be applied to generate the approximate variance–covariance matrix for the within-subject random errors. Hypothesis testing on the linear combinations of the model parameters can be performed by calculating the generalized Wald statistic, distributed approximately as chi-square under the null hypothesis that
β =
0 and
V(O)=0
. These statistical procedures are analogous to the approach described in
Chapter 11 with only minor contextual modifications.
Among various approximation approaches that can be applied to derive Bayes-type estimators of
θ given
F, the Gaussian quadrature derives the most accurate results but is sometimes sensitive to complexity of the covariance structures. In contrast, the MCMC approximation method is not considered to produce analytic results as accurately as the quadrature techniques, but it is empirically more practicable (
McCulloch et al., 2008). Therefore, applicability of the approximation methods varies from situation to situation.
12.3.4. Approximation of variance–covariance matrix for transition probabilities
Approximation of the standard errors for the predicted transition probabilities is an integral part of nonlinear predictions in the application of various multidimensional transition models. In the application of the mixed-effects multinomial logit transition model, the approximation method described in
Chapter 11 can be borrowed to compute the standard errors of the predicted transition probabilities by the delta method.
Let
Lˆiji˜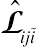
be a random vector of the predicted logit components given prior state
i˜=Yi(j−1)
and
K destination states at time point
j (Lˆiji˜=Lˆiji˜1,Lˆiji˜2,...,Lˆiji˜K)′
with mean
ηiji˜
and the variance–covariance matrix
Σ(Lˆiji˜)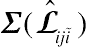
, and
Π˜ˆiji˜=g−1(Lˆiji˜)
is a transform of
Lˆiji˜
, as defined by Equation
(12.12), where g is the logit link function and g
−1 is its inverse. For large samples, the first-order Taylor series expansion of
g−1(Lˆiji˜)
yields approximation of mean
E[g−1(Lˆiji˜)]≈g−1(ηiji˜),
 (12.21)
(12.21)and the variance–covariance matrix
Vˆ(Π˜ˆiji˜)
V[g−1(Lˆiji˜)]≈[∂ g−1(Lˆiji˜)∂ Lˆiji˜∣∣Lˆiji˜=ηiji˜]′Σ(Lˆiji˜)[∂g−1(Lˆiji˜)∂Lˆiji˜∣∣Lˆiji˜=ηiji˜],
 (12.22)
(12.22)where
∂ g−1(Lˆiji˜)∂ Lˆiji˜=[∂g−11(Lˆiji˜1)∂Lˆiji˜1,∂g−12(Lˆiji˜2)∂Lˆiji˜2,...],
and
Σ(Lˆiji˜)=⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜var(Lˆiji˜1) cov(Lˆiji˜1,Lˆiji˜2) ⋅⋅⋅ cov(Lˆiji˜1,Lˆiji˜K) var(Lˆiji˜2) ⋅⋅⋅ cov(Lˆiji˜2,Lˆiji˜K) ⋱ var(Lˆiji˜K)⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟.
 (12.23)
(12.23)In Equation
(12.22), the matrix
V[g−1(Lˆiji˜)]
is the approximate of the variance–covariance matrix
V(Π˜iji˜)
for large samples. For analytic simplicity, this matrix is assumed to be common to all subjects. The square roots of the diagonal elements in this variance matrix yield the standard errors of the predicted transition probabilities contained in the vector
Π˜ˆiji˜
given
βˆ
and
Vˆ(Oˆ)
. As a result, the confidence interval for the predicted probability
π˜ˆijk
can be easily computed.
Bootstrapping has been applied to approximate the standard errors of the predicted transition probabilities in aging and health research. This method, however, provides approximates for a variance–covariance matrix assuming all the off-diagonal elements in
Σ(Lˆiji˜)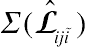
to be 0. Therefore, bootstrapping techniques are not statistically adequate to generate the standard error approximates of the predicted transition probabilities for longitudinal data. In this context, the delta method is a more efficient, robust approximation approach because the matrix
g−1(Lˆiji˜)
is a smooth nonlinear function of
Lˆiji˜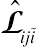
(
Stuart and Ord, 1994) and accounts for the multivariate
data structure in multidimensional health transitions. If the researcher is inclined to use the bootstrapping method due to practical purposes, some covariance structure in the multinomial distribution needs to be assumed for generating a variance– covariance matrix with multivariate normality on the multinomial response.
The approximation of the variance–covariance matrix
Σ(Lˆiji˜)
can be based on the approach described in
Chapter 11, with some minor contextual modifications. First, fit a conditional mixed-effects multinomial logit transition model with all the covariates, including prior state
Yi(j−1)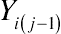
, rescaled to be centered at selected values. Second, use the squared standard error of each intercept estimate in the variance–covariance matrix of the fixed effects, denoted by
Σ(β)
, plus the corresponding variance term of the between-subjects random effects as the variance for each of the
K logit components. Third, take the values of covariance between each pair of the logit intercept estimates in
Σ(θ)
as the off-diagonal elements in
Σ(Lˆiji˜)
. If the covariates are rescaled to be centered at some specified values, the intercepts represent the population-averaged means of the logit components corresponding to the selected covariate values. It follows that the local variance–covariance matrix for the estimated intercepts plus the corresponding variance terms of the between-subjects random effects can be considered approximates of the variance/covariance matrix for the mean multinomial logit function. The empirical application of this approximation method in the mixed-effects multinomial logit transition model is described in
Section 12.4.
Sometimes the difference between two related transition probabilities needs to be tested statistically. For example, some aging and health researchers may be interested in the statistical significance of the difference between two predicted transition probabilities of the same type for two population subgroups. The approach described in
Chapter 11 can be applied for the test, and therefore, the method is not further introduced.
12.3.5. Creation of separate multinomial logit transition models
As the data structure in multidimensional transitions is complex, the researcher may occasionally encounter technical problems in the application of the mixed-effects multinomial logit transition model, such as failure of convergence, numeric instability, or unrealistic values of the parameter estimates. Under these circumstances, a statistically robust alternative approach is to create separate mixed-effects multinomial logit models, with each model being specified for the observations taking a specific value of prior state
Yi(j−1)
(e.g., 0 or 1).
With the specification of a set of separate mixed-effects multinomial logit models, multidimensional transitions in health status or in another outcome type of interest can be analyzed by the application of the mixed-effects multinomial logit model described in
Chapter 11. Let prior state
Yi(j−1)
take only two values, 0 or 1. Then, two separate mixed-effects multinomial logit models can be constructed, with the first model specified for those taking value 0 for
Yi(j−1)
and the second for those taking
value 1. Specifically, the two separate mixed-effects multinomial logit models are written as
log it Pr(Yij=k∣∣Yi(j−1)=0,Xij,b0ik)=X′ijβ0k+Z′ijb0ik+ɛ0ijk,
 (12.24a)
(12.24a)log it Pr(Yij=k∣∣Yi(j−1)=1,Xij,b1ik)=X′ijβ1k+Z′ijb1ik+ɛ1ijk,
 (12.24b)
(12.24b)where parameters
β0k
,
β1k
,
b0ik
, and
b1ik
are specified with subscript 0 or 1 to allow variations in the effects of
Xij
between observations with different prior state values. With the response outcomes at time point
j modeled separately for each prior state, the variable
Yi(j−1)
needs not be included as a predictor on the multinomial logit components and neither is the interaction term between the prior state and another covariate.
Such a modeling strategy by specifying separate regression models on multidimensional transitions makes statistical inference and estimation more parsimonious than the unified transition model. As indicated earlier, this modeling approach usually generates robust, consistent parameter estimates, although it is perhaps not highly statistically efficient. As a subject may be associated with different prior state
Yi(j−1)
at different time points, the data used for each separate model is observation-based rather than subject-specific. Therefore, this approach is recommended for use only when the unified multinomial logit model does not function correctly or when the groups with different prior states are somewhat balanced.
 (12.1)
(12.1) (12.2a)
(12.2a) (12.5)
(12.5) (12.6)
(12.6) (12.7a)
(12.7a) (12.7b)
(12.7b) (12.9)
(12.9) (12.10)
(12.10) (12.11)
(12.11) (12.12)
(12.12) is the estimated multiplicative random error variable for subject i on destination state k (k = 1, …, K) given prior state
is the estimated multiplicative random error variable for subject i on destination state k (k = 1, …, K) given prior state 

 and
and 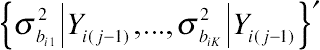 and
and  , respectively, with the latter specified as local approximations that vary over time points. Therefore, this random intercept multinomial logit transition model does not yield a CS pattern in the joint variance–covariance matrix for the predicted transition probabilities unless intrasubject correlation is zero for all subjects with the inclusion of prior state as a covariate. The relative size of
, respectively, with the latter specified as local approximations that vary over time points. Therefore, this random intercept multinomial logit transition model does not yield a CS pattern in the joint variance–covariance matrix for the predicted transition probabilities unless intrasubject correlation is zero for all subjects with the inclusion of prior state as a covariate. The relative size of  determines whether the within-subject random errors can be ignored in predicting the transition probabilities for K + 1 response levels longitudinally.
determines whether the within-subject random errors can be ignored in predicting the transition probabilities for K + 1 response levels longitudinally. (12.13)
(12.13) (12.14)
(12.14) (12.15)
(12.15)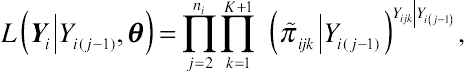 (12.16)
(12.16) (12.17)
(12.17) (12.18)
(12.18) . Analogous to the description in Chapter 11, the differential term is written as
. Analogous to the description in Chapter 11, the differential term is written as  (12.19)
(12.19) (12.20)
(12.20) is a transform of
is a transform of 
 (12.22)
(12.22)
 (12.23)
(12.23) is the approximate of the variance–covariance matrix
is the approximate of the variance–covariance matrix 