CHAPTER 22

SL(n)Examples with Slightly Composite n

In this chapter, we continue to study the object N of Theorem 21.1. Thus k is a finite field of characteristic p, Ã a nontrivial additive character of k, f(x) = ∑^a_i=–b A_ixⁱ ∈ k[x, 1/x] is a Laurent polynomial of “bidegree” (a, b), with a, b both ≥ 1 and both prime to p. We assume that f(x) is Artin-Schreier reduced. We take for N the object N := L_Ã(f(x))(1/2)[1] ∈ P_arith.

Theorem 22.1. The object N, viewed in <N>_geom, is not geometrically isomorphic to the middle convolution of any two objects K and L in <N>_geom each of which has dimension ≥ 2. Equivalently, the representation of G_geom,N corresponding to N is not the tensor product of two other representations of G_geom,N, each of which has dimension ≥ 2.

Proof. The key point is that the object N has no bad characters (because it is totally wildly ramified at both 0 and ∞, a property equivalent to having no bad characters). Therefore every object in <N>_arith shares this property of having no bad characters, cf. Theorem 4.1. In other words, every object M ∈< N >_arith is (strictly speaking, its H^–1(M) is) totally wildly ramified at both 0 and ∞. But every object in <N>_geom is, geometrically, a direct summand of some object of <N>_arith (indeed, of some multiple middle convolution of N and of its Tannakian dual N^∨), so itself is totally wildly ramified at both 0 and ∞. But N has generic rank one, so the theorem results from the following theorem.

Theorem 22.2. Let K and M be two irreducible objects of P_geom, each of which is nonpunctual and totally wildly ramified at both 0 and ∞. Then their middle convolution K ?_mid M has generic rank ≥ 2.

Proof. We have K = K[1] and M = M[1] for irreducible middle extension sheaves K and M on G_m/k, each of which is totally wildly ramified at both 0 and ∞. Over a dense open set U, their middle convolution is of the form Q[1], for Q a lisse sheaf on U whose stalk at a point a ∈ U(k) is the image of the “forget supports” map

H¹_c(G_m/k, K⊗ [x a/x]^? M) → H¹(G_m/k, K⊗ [x a/x]^? M).

We claim that, because K and M are totally wildly ramified at both 0 and ∞, the tensor product sheaf K⊗ [x a/x]^? M is, for all but at most finitely many a, itself totally wildly ramified at both 0 and ∞. Let us temporarily grant this claim. Then for good a, the forget supports map is an isomorphism, and hence the generic rank of Q is

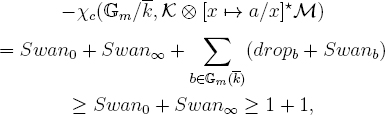
the last inequality because K⊗ [x a/x]^? M is totally wildly ramified at both 0 and ∞. Thus we are reduced to the following lemma, applied to the I(0) (resp. the I(∞)) representations of K and of [x 1/x]^? M.

Lemma 22.3. Let R and S be ℓ-adic representations of I(0) (resp. of I(∞)) which are both totally wildly ramified. Then for all but finitely many a ∈ G_m(k), R ⊗ [x ax]^? S is a totally wild ramified representation of I(0) (resp. of I(∞)).

Proof. We treat the I(0) case; the I(∞) case is identical. The wildness of an ℓ-adic representation of I = I(0) depends only on its restriction to the wild inertia group P = P (0). This restriction is semisimple with finite image, simply because P is a pro-p group, and ℓ ≠ p. So we may replace R and S by their semisimplifications as I-representations, then reduce to the case where R and S are each I-irreducible.

The next step is to reduce further to the case in which R and S are both P-irreducible. We claim that after some Kummer pullback by an n’th power map, for some n prime to p, both R and S are P-isomorphic to direct sums of irreducible P-representations, each of which extends to an I-representation. [Such a Kummer pullback is harmless for questions of total wildness, as P is unchanged.] Recall that once we pick an element ° ∈ I whose pro-order is prime to p and which mod P is a topological generator of the tame quotient I^tame ≅^∧_{Znot p} (1), we have a semidirect product expression

I ≅ P < ° >.

Since R (resp. S) is I-irreducible, conjugation by ° must permute the finitely many isomorphism classes of irreducible P-representations which occur in it. So replacing ° by a prime to p power of itself, which amounts to passing to a Kummer pullback, we get a situation where each P-irreducible in R (resp. in S) is isomorphic to its °-conjugate, hence extends to a representation of I (and the extended representation of I is unique up to tensoring with a Kummer sheaf L_χ, i.e., with a character of I/P = I^tame).

So we are reduced to the case where R and S remain irreducible when restricted to P. If R^∨ and S are inequivalent as P-representations, then (R ⊗ S)^P = Hom_P (R^∨,S) = 0, i.e., R ⊗ S is totally wild. So if no multiplicative translate of S is P-isomorphic to R^∨, we are done.

If some multiplicative translate of S is P-isomorphic to R^∨, say S itself, then (R ⊗ S)^P = Hom_P (R^∨,S) is one-dimensional, with trivial P action, so is some Kummer sheaf L_χ. In this latter case, we have an I-isomorphism

Hom_P (R^∨,S) ⊗ R^∨ ≅ S,

i.e.,

S ≅ R^∨ ⊗ L_χ.

Replacing R by R ⊗ Lχ, which is harmless for questions of total wildness, we must treat the case in which S ≅ R^∨ as I-representation. In view of the previous paragraph, it suffices to show that there are at most finitely many a ∈ G_m(k) such that S is P-isomorphic to [x ax]^? S. In fact, we will show that there are at most Max(Swan(S),Swan(det(S))) such translates.

We first recall [Ka-GKM, 4.1.6 (2)] that there are at most Swan(S) a ∈ G_m(k) such that S is I-isomorphic to [x ax]^–1S. To see this, we consider the canonical extension, say S, of S to a lisse sheaf on G_m which is tame at ∞ and whose I(0)-representation is isomorphic to S. Because S is I-irreducible, S is irreducible as lisse sheaf on G_m/k. If the I-isomorphism class of S is invariant under multiplicative translation by some a ≠ 1 in G_m(k), say by a of multiplicative order n > 1 prime to p, then the isomorphism class of S is invariant under multiplicative translation by µ_n, and hence S descends through the n’th power map, i.e., S ≅ [n]^? T for some lisse sheaf T on G_m, in which case Swan₀(S) = n × Swan₀(T). In particular, n divides Swan₀(S) = Swan(S). So there are at most Swan(S) multiplicative translates of S which are I-isomorphic to S.

We next infer from this that there are at most

Max(Swan(S),Swan(det(S)))

a ∈ G_m(k) such that S is P-isomorphic to [x ax]^? S. Consider first the case in which det(S) is itself wildly ramified. Then applying the above result to det(S), there are at most Swan(det(S)) values a ∈ G_m(k) such that det(S) is I-isomorphic to [x ax]^? det(S). But taking a Kummer sheaf L_χ which has the same value on ° as det(S), the ratio det(S)/L_χ is a wild character which takes only p-power roots of unity as values. Indeed, as S has p-power rank (being P-irreducible), we may replace S by its twist by the unique rank(S)’th root of L_χ, and reduce to the case where det(S) has p-power order. In this case, det(S) is a character of I ≅ P < ° > which is trivial on °, so is completely determined by its restriction to P. So in this case, the P -isomorphism class of det(S) is preserved by at most Swan(det(S)) multiplicative translations.

Now consider the case in which det(S) is tame. Here the I-isomorphism class of det(S) is invariant by multiplicative translation. But one knows that for an irreducible representation S of I which is P-irreducible, its I-isomorphism class is determined by the two data consisting of the P-isomorphism class of S and the I-isomorphism class of det(S), cf. [Ka-ClausCar, 2.5.1]. [Indeed, as noted earlier, if S₁ and S₂ are P-irreducible and P-isomorphic, then for some χ, S₁ ≅ S₂ ⊗ L_χ. Taking determinants, we get det(S₁) ≅ det(S₂) ⊗ L_χ^q, for q the common rank of the S_i. But q is some power q of p, by P-irreducibility, so if the determinants are isomorphic then χ is trivial.] Since the I-isomorphism class of S is preserved by at most Swan(S) translations, the same is true for its P-isomorphism class.

Theorem 22.4. We have the following result concerning the object N of Theorem 21.1. Suppose that a ≠ b, that gcd{i|A_i ≠ 0} = 1, and that (–1)^aaA_a = (–1)^b+1bA_–b. Suppose further that a + b is the product ℓ₁ℓ₂ of two distinct primes. Then G⁰_geom ⊂ SL(ℓ₁ℓ₂), already shown to be a connected irreducible subgroup which is not self-dual, has a simple Lie algebra.

Proof. We argue by contradiction. If Lie(G⁰_geom) is not simple, then G⁰_geom is the image in SL(ℓ₁ℓ₂) of a product group G₁ × G₂, with G₁ ⊂ SL(ℓ₁) and G₂ ⊂ SL(ℓ₂) connected irreducible subgroups, at least one of which is not self-dual, under the tensor product of the given representations.

Suppose first that 2 = ℓ₁. Then for lack of choice G₁ = SL(2), and hence by Gabber’s theorem on prime-dimensional representations [Ka-ESDE, 1.6], G₂ must be SL(ℓ₂), the only non-self-dual choice. The image of this G₁ × G₂ in SL(ℓ₁ℓ₂) is this product group, and it is its own normalizer in SL(ℓ₁ℓ₂). Therefore G_geom = G₁ × G₂. This contradicts Theorem 22.1.

Suppose now that both ℓ₁ and ℓ₂ are odd primes. Then at least one of the factors, say G₁, is not self-dual, so must be SL(ℓ₁). The second factor G₂ is either SL(ℓ₂) or SO(ℓ₂) or SO(3), viewed as the image of SL(2) in Sym^ℓ₂–1(std₂), or, if ℓ₂ = 7, possibly the exceptional group G2 in its seven-dimensional representation. In this case as well, the image of G₁ × G₂ in SL(ℓ₁ℓ₂) is this product group, and its normalizer in SL(ℓ₁ℓ₂) is itself, augmented by the scalars µ_ℓ1ℓ2 in SL(ℓ₁ℓ₂). In the case when G₂ is SL(ℓ₂), these scalars are already in G₁ × G₂, so G₁ × G₂ is its own normalizer in SL(ℓ₁ℓ₂). So in this case G_geom is the product group G₁ × G₂, and we contradict Theorem 22.1.

If G₂ is SO(ℓ₂) or one of its listed subgroups, G₂ contains no nontrivial scalars, so the normalizer of G₁ × G₂ in SL(ℓ₁ℓ₂) is the product group

G₁ × (µ_ℓ2 × G₂).

Thus we have

G₁ × ×G₂ ⊂ G_geom ⊂ G₁ × (µ_ℓ2 × G₂).

So G_geom is either G₁ × × G₂ or it is G₁ × (µ_ℓ2 × G₂), in either case contradicting Theorem 22.1.

Remark 22.5. In view of this result, it is natural to ask the following question: for which pairs of distinct primes ℓ₁ < ℓ₂ is it the case that the only connected irreducible subgroup of SL(ℓ₁ℓ₂) which is not self-dual, and whose Lie algebra is simple, is the entire group SL(ℓ₁ℓ₂) itself? Such a subgroup is the image of an irreducible, non-self-dual, ℓ₁ℓ₂-dimensional representation of a simply connected group with simple Lie algebra. We wish to know the cases in which the only such are the standard representation std_ℓ1ℓ2 of SL(ℓ₁ℓ₂) and its contragredient. One knows that only the types A_n, n ≥ 2, D_{2k+ 1}, k ≥ 2, and E₆ have irreducible representations which are not self-dual. According to a recent result of Goldstein, Guralnick and Stong [GGS, Cor. 1.5], only the A_n, n ≥ 2, have irreducible representations which are non-self-dual and of dimension equal to the product ℓ₁ℓ₂ of two distinct primes ℓ₁ < ℓ₂. Moreover, the only dimensions ℓ₁ℓ₂ so attained are of the following three types.

(1) Twin primes: ℓ₂ = ℓ₁ + 2. In general, n(n+ 2) is the dimension of the representation !₁ + (n – 1)!₂ of A₂.

(2) Sophie Germain primes: ℓ₂ = 2ℓ₁ + 1. In general, n(2n + 1) is the dimension of the representation Sym²(std_2n) of SL(2n), or the dimension of the representation Λ²(std_{2n+ 1})of SL(2n+ 1), or the dimension of the representation Sym^{2n+ 1}(std₃)of SL(3).

(3) Variant Sophie Germain primes: ℓ₂ = 2ℓ₁ – 1. In general, n(2n–1) is the dimension of the representation Sym²(std_2n–1) of SL(2n–1), or the dimension of the representation Λ²(std_2n) of SL(2n), or the dimension of the representation Sym²ⁿ(std₃) of SL(3).

Thus we obtain the following theorem.

Theorem 22.6. We have the following result concerning the object N of Theorem 21.1. Suppose that a ≠ b, that gcd{i|A_i ≠ 0} = 1, and that (–1)^aaA_a = (–1)^{b+ 1}bA_–b. Suppose further that a + b is the product ℓ₁ℓ₂ of two distinct primes ℓ₁ < ℓ₂. Suppose that these are neither twin primes, Sophie Germain primes, or variant Sophie Germain primes. Then G_geom = SL(ℓ₁ℓ₂).

Remark 22.7. Thus for example if ℓ₁ℓ₂ < 400 and (ℓ₁, ℓ₂) is not any of

(2, 3), (2, 5), (3, 5), (3, 7), (5, 7), (5, 11), (7, 13), (11, 13), (11, 23), (17, 19), then we have G_geom = SL(ℓ₁ℓ₂) in the theorem above. This can be seen directly, i.e., without invoking [GGS, Cor. 1.5], from the tables of Lübeck [Lu]. In these tables, the dimensions listed as valid for all large p are also the dimensions of the same representations of the complex group.