CHAPTER 30

Appendix: Deligne’s Fibre Functor

In this appendix, we prove Theorem 3.1, i.e., we show that N !(N) := H⁰(A¹/k, j_0!N) is a fibre functor on the Tannakian category P_geom of those perverse sheaves on G_m/k satisfying P, under middle convolution. Throughout this appendix, we work entirely over k, explicit mention of which we will omit. Thus we will write !(N) simply as H⁰(A¹, j_0!N). And when we wish to emphasize the roles of both 0 and ∞ in its definition, we will write it as !(N) := H⁰(P¹, Rj_∞?j_0!N) = H⁰(P¹, j_0!Rj_∞?N).

It will be convenient to define, for any object M ∈ D^b_c(G_m, Q_ℓ),

!(M) := H^?(P¹, j_0!Rj_∞?M) := ⊕_i∈ZHⁱ(P¹, j_0!Rj_∞?M).

Lemma 30.1. If M is perverse, then Hⁱ(P¹, j_0!Rj_∞?M) = 0 for i ≠ 0, and dim H⁰(P¹, j_0!Rj_∞?M) = χ(G_m, M)(= χ_c(G_m, M)). The functor M !(M) is an exact, faithful functor from the category Perv/Neg to the category of finite dimensional Q_ℓ-vector spaces.

Proof. We can also write H^?(P¹, j_0!Rj_∞?M) as H^?(A¹, j_0!M). Thus the first assertion was proven in Lemma 3.4. The dimension formula shows that !(M) = 0 if and only if M is negligible. The (not very) long exact cohomology sequence shows that ! is exact on Perv/Neg, and kills precisely the negligible objects.

Suppose now that K and N are both in P_geom. Then both K ?_! N and K ?_? N lie are perverse, and K?_mid is, by definition, the image of the “forget supports” map K ?_! N → K ?_? N. By Gabber-Loeser [Ga-Loe, 3.6.4], both the kernel and cokernel of this map are negligible perverse sheaves, i.e., with χ = 0. Hence we get

Lemma 30.2. For K and N in P_geom, under the natural maps

K ?_! N K ?_mid N K ?_? N,

the induced maps on !’s are isomorphisms

!(K ?_! N) ≅ !(K ?_mid N) ≅ !(K ?_? N).

Lemma 30.3. For M perverse, with M^∨ := [x 1/x]^? DM, !(M^∨) is the linear dual of !(M).

Proof. Indeed,

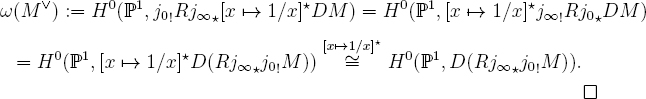
Lemma 30.4. Given two objects K and N in P_geom, we have the formula

dim(!(K) ⊗ !(N)) = dim !(K ?_! N),

i.e., we have

χ(G_m, K) × χ(G_m, N) = χ(G_m, K ?_! N).

Proof. Indeed, for mult : G_m × G_m → G_m the multiplication map, we have K ?_! N = R(mult)_!(K £ N). Thus

We now turn to the proof of Theorem 3.1. Given two objects K and N in P_geom, we will define bifunctorial maps

!(K)⊗!(N) → !(K ?_!N) ≅ !(K ?_midN) ≅ !(K ?_? N) → !(K)⊗!(N),

and show that their composite is the identity on !(K) ⊗ !(N). This is all we need: each of the five terms has dimension χ(G_m, K)×χ(G_m, N), so once the composite map is the identity, then the first map is injective and hence, for dimension reasons, an isomorphism. This isomorphism gives the required bifunctorial isomorphism

!(K) ⊗ !(N) ≅ !(K ?_mid N).

We begin with the construction of the map

!(K) ⊗ !(N) → !(K ?_! N).

Let us define

K := j_0!Rj_∞? K, N := j_0!Rj_∞? K.

Then we have

!(K) = H^? (P¹, K), !(N) = H^? (P¹, N),

and hence we have

!(K) ⊗ !(N) = H^? (P¹ × P¹, K £ N).

We would like to extend the multiplication map G_m × G_m → G_m to a map P¹ × P¹ → P¹. We cannot do this, but if we omit from P¹ × P¹ the two points (0, ∞) and (∞, 0), then we can define a map

π : P¹ × P¹ {(0, ∞), (∞, 0)} → P¹,

given in homogeneous coordinates (A, B), (X, Y) on P¹ × P¹ by

((A, B), (X, Y)) (AX, BY).

Over the open set G_m in the target, we have the multiplication map G_m × G_m → G_m. Over the point 0 in the target, the fibre π^–1(0) is the union of 0 × A¹ with A¹ × 0. Notice that because both K and N vanish at 0, the restriction of K £ N to π^–1(0) vanishes. [The fibre π^–1(∞) is the union of ∞× (P¹ 0) with (P¹ 0) ×∞, a fact we will use later.]

Because K £ N vanishes at both the points (0, ∞) and (∞, 0), we have an isomorphism

H^?_c(P¹ × P¹ {(0, ∞), (∞, 0)}, K £ N) ≅ H^? (P¹ × P¹, K £ N).

Slightly less obvious is the following lemma.

Lemma 30.5. The restriction map in ordinary cohomology gives an isomorphism

H^? (P¹ × P¹, K £ N) ≅ H^? (P¹ × P¹ {(0, ∞), (∞, 0)}, K £ N).

Proof. It suffices to show that, denoting by i_(0,∞) and i_(∞,0) the inclusions, we have

Ri^!_{(0, ∞)}(K £ N) = 0, Ri^!_{(∞, 0)}(K £ N) = 0.

By duality, this is equivalent to

i^?_{(0, ∞)}(DK £ DN) = 0, i^?_{(∞, 0)}(DK £ DN) = 0.

But both DK = Rj_0?j_∞!DK and DN = Rj_0?j_∞!DN vanish at ∞, so their external product DK £ DN vanishes at both the points (0, ∞) and (∞, 0).

So our situation now is that we have isomorphisms

H^?_c(P¹×P¹{(0, ∞), (∞, 0)}, K£N) ≅ H^? (P¹×P¹, K£N) = !(K)⊗!(N)
= H^? (P¹ × P¹, K £ N) ≅ H^? (P¹ × P¹ {(0, ∞), (∞, 0)}, K £ N),

in which the composite isomorphism is the “forget supports” map.

By the Leray spectral sequence for π in compact cohomology, we have

H^?_c(P¹ × P¹ {(0, ∞), (∞, 0)}, K £ N) = H^? (P¹, Rπ_!(K £ N)).

And by the Leray spectral sequence in ordinary cohomology, we have

H^? (P¹ × P¹ {(0, ∞), (∞, 0)}, K £ N) ≅ H^? (P¹, Rπ_? (K £ N)).

So we have isomorphisms

H^? (P¹, Rπ_!(K £ N)) ≅ !(K) ⊗ !(N) ≅ H^? (P¹, Rπ_? (K £ N)),

in which the composite map is induced by the “forget supports” map Rπ_!(K £ N) → Rπ_? (K £ N).

There are two further isomorphisms we now take into account. As already observed above, K £ N vanishes on the fibre π^–1(0), so by proper base change Rπ_!(K£N) vanishes at 0, and hence the adjunction map j_0!j₀^? → id induces an isomorphism

j_0!j₀^? Rπ_!(K £ N) ≅ Rπ_!(K £ N).

We claim that, dually, the adjunction map id → Rj_∞?j_∞^? induces an isomorphism

Rπ_? (K £ N) ≅ Rj_∞? j_∞^? Rπ_? (K £ N).

Indeed, this is equivalent, by duality, to the statement that the adjunction map j_∞!j_∞^? → id induces an isomorphism

j_∞!j_∞^? Rπ_!(DK £ DN) ≅ Rπ_!(DK £ DN).

This holds, because both DK and DN vanish at ∞, so their external product DK £ DN vanishes on π^–1(∞) (which we noted above is the union of ∞× (P¹ 0) with (P¹ 0) ×∞), and we get the assertion by proper base change.

Applying the adjunction map id → Rj_∞ j_∞^?, we get a map

j_0!j₀^? Rπ_!(K £ N) → Rj_∞?j_∞^? j_0!j₀^? Rπ_!(K £ N).

Here the cohomology of the target is !(K_! N).

Applying the adjunction map j_0!j₀^? → id, we get a map

j_0!j₀^? j_∞!j_∞ Rπ_? (DK £ DN) → j_∞!j_∞^? Rπ_? (DK £ DN).

Here the cohomology of the target is !(K_ℓ N).

So the situation now is that we have a diagram of horizontal “forget supports” maps and vertical adjunction maps as follows. To make the diagram fit horizontally on the page, we write S for the subset {(0, ∞), (∞, 0)} of P¹ × P¹. Thus

P¹ × P¹ S := P¹ × P¹ {(0, ∞), (∞, 0)},

and our diagram is this.

So what must be shown is the commutativity of the following diagram.

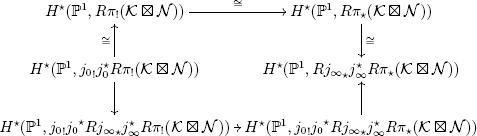
To see what is going on, let us define

A := Rπ_!(K £ N), B := Rπ_? (K £ N),

and denote by f : A → B the “forget supports” map. Then the diagram in question is gotten by applying the functor C H^? (P¹, C) to the following diagram.

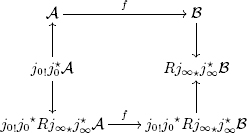
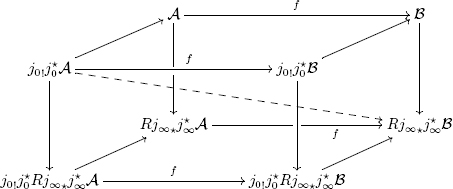
It suffices to show this this last diagram is commutative. To see this, we embed into the larger diagram, in which all the vertical and inward facing arrows are adjunctions, and all the horizontal arrows are induced by f.

A diagram chase shows that it suffices to show that the top face, the right side face, and the front face are each commutative. The top face is obtained by applying the adjunction j_0!j^?₀ → id to the morphism f; it is commutative by the functoriality of adjunction. The right side face is obtained by applying the adjunction id → Rj_∞? j^?_∞ to the (adjunction) morphism j_0!j^?₀B → B, so is commutative by the functoriality of adjunction. And the front face is obtained by applying the same adjunction to the morphism j_0!j^?₀(f), so is again commutative. [In fact, all six faces are commutative, always by the functoriality of adjunction.] This concludes the proof of Theorem 3.1.