1.2. Common Cryptographic Primitives

As claimed at the outset of this chapter, it is rather difficult to give a precise definition of the term cryptography. The best way to understand it is by examples. In this section, we briefly describe the common problems that cryptography deals with.

1.2.1. The Classical Problem: Secure Transmission of Messages

To start with, we introduce the legendary figures of cryptography: Alice, Bob and Carol. Alice wants to send a message to Bob over a public communication channel like the Internet and wants to ensure that nobody other than Bob can make out the meaning of the message. A third party like Carol, who has access to the communication channel, can intercept the message. But the message should be wrapped or transformed before transmission in such a way that knowledge of some secret piece of information is needed to unwrap or transform back the message. It is Bob who has this information, but not Carol (nor Dorothy nor Emily nor . . .).

It is expedient to point out here that Alice, Bob and Carol need not be human beings. They can stand for organizations (like banks) or, more correctly, for computers or computer programs run by individuals or organizations. It is, therefore, customary to call them parties, entities or subjects instead of persons or characters. In the cryptology jargon, Carol has got several names used interchangeably: adversary, eavesdropper, opponent, intruder, attacker and enemy are the most common ones. When a message transmission like that just mentioned is involved, Alice is called the sender and Bob is called the receiver of the message.

It is a natural strategy to put the message in a box and lock the box using a key, called the encryption key. A matching decryption key is needed to unlock the box and retrieve the message. The process of putting the message in the box is commonly called encoding and that of locking the box is called encryption. The reverse processes, namely unlocking the box and taking the message out of the box are respectively called decryption and decoding. This is precisely the classical encryption–decryption protocol of cryptography.^[1]

^[1] Some people prefer to use the terms enciphering and deciphering in place of the words encryption and decryption respectively.

In the world of electronic communication, a message M is usually a bit string, and encoding, encryption, decryption and decoding are well-defined transformations of bit strings. If we denote by f_e the transformation function consisting of encoding and encryption, then we get a new bit string C = f_e(M, K_e), where K_e stands for the encryption key. This bit string C is sent over the communication channel. After Bob receives C, he uses the reverse transformation f_d (decryption followed by decoding) to get the original message M back; that is, M = f_d(C, K_d). Note that the decryption key K_d is needed as an argument to f_d. If Carol does not know this, she cannot compute M. We conventionally call M the plaintext message and C the ciphertext message.

The encoding and decoding operations do not make use of keys and can be performed by anybody. (It should not be difficult to put a letter in or take a letter out of an unlocked box!) One might then wonder why it is necessary to do these transformations instead of applying the encryption and decryption operations directly on M and C respectively. With whatever we have discussed so far, we cannot give a full answer to this question. For the answer, we will need to wait until we reach the later chapters. We only mention here that the encryption algorithms often require as input some mathematical entities (like integers or elements of a field) which are logically not bit strings. But that’s not all! As we see later, the additional transformations often add to the security of the protocols. On the other hand, for a general discussion, it is often unnecessary to start from the encoding process and end at the decoding process. As a result, we will assume, unless otherwise stated, that M is the input to the encryption routine and the output of the decryption routine, in which case f_e and f_d stand for the encryption and decryption functions only.

Symmetric-key or secret-key cryptography

In the simplest form of locking mechanism, one has K_e = K_d. That is, the same key, called the symmetric key or the secret key, is used for both encryption and decryption. Common examples of such symmetric-key algorithms include DES (Data Encryption Standard) together with its various modifications like the Triple DES and DES-X, IDEA (International Data Encryption Algorithm), SAFER (Secure And Fast Encryption Routine), FEAL (Fast Encryption Algorithm), Blowfish, RC5 and AES (Advanced Encryption Standard). We will not describe all these algorithms in this book. Interested readers can look at the abundant literature to know more about them.

Asymmetric-key or public-key cryptography

The biggest disadvantage of using a secret-key system is that Alice and Bob must agree upon the key K_e = K_d secretly, for example by personal contact or over a secure channel. This is a serious limitation and is not often practical nor even possible. Another drawback of secret-key systems is that every pair of parties needs a key for communication. Thus, if there are n entities communicating over a net, the number of keys would be of the order of n². Also, each entity has to remember O(n) keys for communicating with other entities. In practice, however, an entity does not communicate with every other entity on the net. Yet the total number of keys to be remembered by an entity could be quite high.

Both these problems can be avoided by using what is called an asymmetric-key or a public-key protocol. In such a protocol, each entity decides a key pair (K_e, K_d), makes the encryption key K_e public and keeps the decryption key K_d secret. K_e is also called the public key and K_d the private key. Anybody who wants to send a message to Bob gets Bob’s public key, encrypts the message with the key, and sends the ciphertext to Bob. Upon receiving the ciphertext, Bob uses his private key to decrypt the message. One may view such a lock as a self-locking padlock. Anybody can lock a box with a self-locking padlock, but opening it requires a key which only Bob possesses.

The source of security of such a system is based on the difficulty of computing the private key K_d given the public key K_e. It is apparent that K_e and K_d are sort of inverses of each other, because the former is used to generate C from M and the latter is used to generate M from C. This is where mathematics comes into the picture. We mention a few possible constructions of key pairs in the next section and the rest of the book deals with an in-depth study of these public-key protocols.

Attractive as it looks, public-key protocols have a serious drawback, namely they are orders of magnitude slower than their secret-key counterparts. This is of concern, if huge amounts of data need to be encrypted and decrypted. This shortcoming can be overcome by using both secret-key and public-key protocols in tandem as follows: Alice generates a secret key (say, for AES), encrypts the message by the secret key and the secret key by the public key of Bob and sends both the encrypted message and the encrypted secret key. Bob first decrypts the encrypted secret key using his private key and uses this decrypted secret key to decrypt the message. Since secret keys are usually short bit strings (most commonly of length 128 bits), the slow performance of the public-key algorithms causes little trouble. But at the same time, Alice and Bob are relieved of having a previous secret meeting or communication for agreeing on the secret key. Moreover, neither Alice nor Bob needs to remember the secret key. During every session of message transmission, a random secret key can be generated and later destroyed, when the communication is over.

1.2.2. Key Exchange

There is an alternative method by which Alice and Bob can exchange secret information (like AES keys) over a public communication channel. Let us first see how this can be done in the physical lock-and-key scenario. Alice generates a secret, puts it in a box, locks the box with her own key and sends it to Bob. Bob, upon receiving the locked box, adds a second lock to it and sends the doubly locked box back to Alice. Alice then removes her lock and again sends the box to Bob. Finally, Bob uses his key to unlock the box and retrieve the secret. A third party (Carol) that can access the box during the three communications finds it locked by Alice or Bob or both. Since Carol does not possess the keys to these locks, she cannot open the box to discover the secret.

This process can be abstractly described as follows: Alice and Bob first independently generate key pairs (A_Ke, A_Kd) and (B_Ke, B_Kd) respectively. Alice then sends A_Ke to Bob and Bob sends B_Ke to Alice. The private keys A_Kd and B_Kd are not disclosed. They also agree upon a function g with which Alice computes g_A = g(A_Kd, B_Ke) and Bob computes g_B = g(B_Kd, A_Ke). If g_A = g_B, then this common value can be used as a shared secret between Alice and Bob.

Our intruder Carol knows g and taps the values of A_Ke and B_Ke. So the function g should be such that a knowledge of these values alone does not suffice for the computation of g_A = g_B. One of the private keys A_Kd or B_Kd is needed for the computation. Since (A_Ke, A_Kd) and (B_Ke, B_Kd) are key pairs, it is assumed that private keys are difficult to compute from the knowledge of the corresponding public keys.

Such a technique of exchanging secret values over an insecure channel is called a key-exchange or a key-agreement protocol. It is important to point out here that such a protocol is usually based on the public-key paradigm; that is to say, we do not know secret-key counterparts for a key-exchange protocol. Since a shared secret between the communicating parties is usually short, the low speed of public-key algorithms is really not a concern in this case.

1.2.3. Digital Signatures

A digital signature is yet another application of the public-key paradigm. Suppose Alice wants to sign a message M in such a way that the signature S can be verified by anybody but nobody other than Alice would be able to generate the signature S on the message M. This can be achieved as follows: Alice generates a key pair (K_e, K_d), makes K_e public and keeps K_d secret. She now uses the decryption function f_d to generate the signature, that is, S = f_d(M, K_d). The signature S is then made public. Anybody who has access to Alice’s public key K_e applies the reverse transformation f_e to get back the message M = f_e(S, K_e).

If Carol signs the message M with a different key , then she generates the signature S′ = f_d(M, ). Now, since and K_e are not matching keys, verification using K_e gives M′ = f_e(S′, K_e), which is different from M. If we assume that M is a message written in a human-readable language (like English), then M′ would generally look like a meaningless sequence of characters which is neither English nor any sensible string to a human reader. So the signature verifier would then immediately conclude that this is a case of forged signature.

Such a scheme of generating digital signatures is called a signature scheme with message recovery. It is obvious that this is the same as our encrypt–decrypt scheme with the sequence of encryption and decryption steps reversed. If the message M to be signed is quite long, using this algorithm calls for a large execution time both for signature generation and for verification. It is, therefore, customary to use another variant of signature schemes called signature schemes with appendix that we describe now.

Instead of applying the decryption transform directly on M, Alice first computes a short representative H(M) of her message M. Her signature now becomes the pair S = (M, σ), where σ = f_d(H(M), K_d). Typically, a hash function (see Section 1.2.6) is used to compute the representative H(M) from M and is assumed to be a public knowledge. Now anybody can verify the signature by checking if the equality H(M) = f_e(σ, K_e) holds. If a key different from K_d is used to generate the signature, one would (in general) get a value σ′ ≠ σ and the signature forging will be detected by observing that H(M) ≠ f_e(σ′, K_e).

1.2.4. Entity Authentication

By entity authentication, we mean a process in which one entity called the claimant proves its identity to another entity called the prover. Entity-authentication techniques, thus, tend to prevent impersonation of an entity by an intruder. Both secret-key and public-key techniques are used for entity-authentication schemes.

The simplest example of an entity-authentication scheme is the use of passwords, as in a computer where a user (the claimant) tries to gain access to some resources in a computer (the prover) by proving its identity using a password. Password schemes are mostly based on secret-key techniques. For example, the UNIX password system is based on encrypting the zero message (a string of 64 zero bits) using a repeated application of a variant of the DES algorithm with 64 bits of the user input (the password) as the key. Password-based authentication schemes are fixed and time-invariant and are often called weak authentication schemes.

We see applications of public-key techniques in challenge–response authentication schemes (also called strong authentication schemes). Assume that an entity, Alice, wants to prove her identity to another entity, Bob. Alice generates a key pair (K_e, K_d), makes K_e public and keeps K_d secret. Now, Bob chooses a random message M, encrypts M using Alice’s public key—that is, computes C = f_e(M, K_e)—and sends C to Alice. Alice, upon reception of C, decrypts it using her private key K_d; that is, she regenerates M = f_d(C, K_d) and sends M to Bob. Bob compares this value of M with the one he generated, and if a match occurs, Bob becomes sure that the entity who is claiming to be Alice possesses the knowledge of Alice’s private key. If Carol uses any private key other than K_d for the decryption, she gets a message M′ different from M and thereby cannot prove to Bob her identity as Alice. This is how this scheme prevents impersonation of Alice by Carol.

Entity authentication is often carried out using another interesting technique called zero-knowledge proof. In such a protocol, the prover (or any third party listening to the conversation) gains no knowledge regarding the secret possessed by the claimant, but develops the desired confidence regarding the claim by the claimant of the possession of the secret. We provide here an informal example explaining zero-knowledge proofs.

Let us think of a circular cave as shown in Figure 1.1. The cave has two exits, left and right, denoted by L and R respectively. The cave also has a door inside it, which is invisible outside the cave. Alice (A) wants to prove to Bob (B) that she possesses a key to this door without showing him the key or the process of unlocking the door with the key. Bob stations himself somewhere outside the exits of the cave. Alice enters the cave and randomly chooses the left or right wing of the cave (and goes there). She does not disclose this choice to Bob, because Bob is not allowed to know the session secrets too. Once Alice is placed in the cave, Bob makes a random choice from L and R and asks Alice (using cell phones or by shouting loudly) to come out of the cave via that chosen exit. Suppose Bob challenges Alice to use L. If Alice is in the left wing, she can come out of the cave using L. If Alice is in the right wing, she must use her secret key to open the central door to come to the left wing and then go out using exit L. If Alice does not possess the secret key, she can succeed in obeying Bob’s directive with a probability of half. If this procedure is repeated t times, then the probability that Alice succeeds on all occasions without possessing the secret key is (1/2)^t = 1/2^t. By choosing t appropriately, Bob can make the probability of accepting a false claim arbitrarily small. For example, if t = 20, then the chance is less than one in a million that Alice can establish a false claim.

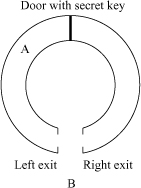
Thus, if Alice succeeds every time, Bob gains the desired confidence that Alice actually possesses the secret. However, during this entire process, Bob can obtain no information regarding Alice’s secrets (the key and the choices of wings). Another important aspect of this interaction is that Alice has no way of predicting Bob’s questions, preventing impostors (of Alice) from fooling Bob.

1.2.5. Secret Sharing

Suppose that a secret piece of information is to be distributed among n entities in such a way that n – 1 (or fewer) entities are unable to construct the secret. All of the n entities must participate to reveal the secret. As usual, let us assume that the secret is an l-bit string. A simple strategy would be to break the string into n parts and provide each entity with a part. This method is, however, not really attractive, because it gives partial information about the secret. Thus, for example, if a 256-bit long bit string is to be distributed equally among 16 entities, any 15 of them working together can reconstruct the secret by trying only 2¹⁶ = 65536 possibilities for the unknown 16 bits.

We now describe an alternative strategy that does not suffer from this drawback. Once again, we break the secret string into n parts and consider the parts as integers a₀, . . . , a_n–1. We construct the polynomial f(x) = xⁿ+a_n–1x^n–1 + · · · + a₁x+a₀ and give the integers f(1), f(2), . . . , f(n) to the entities. When all of the entities cooperate, the linear system of equations f(i) = iⁿ + a_n–1i^n–1 + · · · + a₁i + a₀, 1 ≤ i ≤ n, can be solved to find out the unknown coefficients a₀, . . . , a_n–1 which, in turn, reveal the secret. On the other hand, if n – 1 or less entities cooperate, they get an underspecified system of equations in n unknowns, from which the actual solution is not readily available.

The secret-sharing problem can be generalized in the following way: to distribute a secret among n parties in such a way that any m or more of the parties can reconstruct the secret (for some m ≤ n), whereas any m – 1 or less parties cannot do the same. A polynomial of degree m as in the above example readily adapts to this generalized situation.

1.2.6. Hashing

A function which converts bit strings of arbitrary lengths to bit strings of a fixed (finite) length is called a hash function. Hash functions play a crucial role in cryptography. We have already seen an application of it for designing a digital signature scheme with appendix. If H is a hash function, a pair of input values (strings) x₁ and x₂ for which H(x₁) = H(x₂) is called a collision for H. For any hash function H, collisions must exist, since H is a map from an infinite set to a finite set. However, for cryptographic purposes we want that collisions should be difficult to obtain. More specifically, a cryptographic hash function H should satisfy the following desirable properties:

First pre-image resistance

Except for a small set of hash values y it should be difficult to find an input x with H(x) = y. We exclude a small set of values, because an adversary might prepare (and maintain) a list of pairs (x, H(x)) for certain values of x of her choice. If the given value of y is the second coordinate of one pair in her list, she can produce the corresponding input value x easily.

Second pre-image resistance

Given a pair (x, H(x)), it should be difficult to find an input x′ different from x with H(x) = H(x′).

Collision resistance

It should be difficult to find two different input strings x, x′ with H(x) = H(x′).

Hash functions are also called message digests and can be used with a secret key. Popular examples of unkeyed hash functions are SHA-1, MD5 and MD2, whereas those for keyed hash functions include HMAC and CBCMAC.

1.2.7. Certification

So far we have seen several protocols which are based on the use of public keys of remote entities, but have never questioned the authenticity of public keys. In other words, it is necessary to ascertain that a public key is really owned by a remote entity. Public-key certificates are used to that effect. These are data structures that bind public-key values to entities. This binding is achieved by having a trusted certification authority digitally sign each certificate.

Typically a certificate is issued for a period of validity. However, it is possible that a certificate becomes invalid before its date of expiry for several reasons, like possible or suspected compromise of the private key. Under such circumstances it is necessary that the certification authority revokes the certificate and maintains a list called certificate revocation list (CRL) of revoked certificates. When Alice verifies the authenticity of Bob’s public-key certificate by verifying the digital signature of the authority and does not find the certificate in the CRL, she gains the desired confidence in using Bob’s public key.

The X 5.09 public-key infrastructure specifies Internet standards for certificates and CRLs.