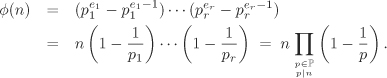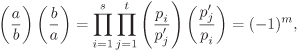2.5. Integers

The set of integers is the main object of study in this section. We use many results from previous sections to derive properties of integers. Recall that is a PID and hence a UFD.

2.5.1. Divisibility

The notions of divisibility, prime and relatively prime integers, gcd and lcm of integers are essentially the same as discussed in connection with a PID or a UFD. We avoid repeating the definitions here, but concentrate on other useful properties of integers, not covered so far. We only mention that whenever we talk about a prime integer, or the gcd or lcm of two or more integers, we will usually refer to a non-negative integer. This convention makes primes, gcds and lcms unique.

Theorem 2.12.

There are infinitely many prime integers. Proof Let be arbitrary and let p1, p2, . . . , pn be n distinct primes. The (non-zero non-unit) integer q := p1p2 · · · pn + 1 is divisible by neither of p1, . . . , pn and hence must have a prime divisor pn+1 different from p1, . . . , pn. The result then follows by induction on n (and the fact that the set of primes is non-empty).

Theorem 2.13.

For an integer a and an integer b ≠ 0, there exist unique integers q and r such that a = qb + r with 0 ≤ r < |b|. Proof Call the smallest non-negative element in the set to be r and the corresponding value of c to be q. Then these integers q and r satisfy the desired properties. To prove the uniqueness let a = q1b + r1 = q2b + r2, where 0 ≤ r1 < |b| and 0 ≤ r2 < |b|. But then (q2 – q1)b = r1 – r2 with –|b| < r1 – r2 < |b|. Since b|(r1 – r2), we must then have r1 – r2 = 0, that is, r1 = r2, which, in turn, implies that q1 = q2.

The integers q and r in the above theorem are respectively called the quotient and the remainder of Euclidean division of a by b and are denoted respectively by a quot b and a rem b. Do not confuse Euclidean division with the division (that is, the inverse of multiplication) of the ring . Euclidean division is the basis of the Euclidean gcd algorithm. More specifically:

Proposition 2.15.

For integers a, b with b ≠ 0, let r be the remainder of Euclidean division of a by b. Then gcd(a, b) = gcd(b, r). Proof Clearly, 〈a〉 + 〈b〉 = 〈r〉 + 〈b〉. Now use Proposition 2.14.

Proposition 2.16.

Let a and b be two integers, not both zero, and let d be the (positive) gcd of a and b. Then there are integers u and v such that d = ua + vb. (Such an equality is called a Bézout relation.) Furthermore, if a and b are both non-zero and (|a|, |b|) ≠ (1, 1), then u and v can be so chosen that |u| < |b| and |v| < |a|. Proof The existence of u and v follows immediately from Proposition 2.14. If a = qb, then u = 0 and v = 1 is a suitable choice. So assume that a  b and b  a, in which case d < |a| and d < |b|. We may assume, without loss of generality, that a and b are positive. First note that if (u, v) satisfies the Bézout relation, then for any the pair (u + kb, v – ka) also satisfies the same relation. So we may replace v by its remainder of Euclidean division by a and may assume |v| < a. But then |ua| – b < |ua| – d ≤ |ua – d| = |vb| ≤ (a – 1)b, which implies |u| < b.

The notions of the gcd and of the Bézout relation can be generalized to any finite number of integers a₁, . . . , a_n as

gcd(a₁, . . . , a_n) = gcd(· · · (gcd(gcd(a₁, a₂), a₃) · · ·), a_n) = u₁a₁ + · · · + u_na_n

for some integers u₁, . . . , u_n (provided that all the gcds mentioned are defined).

2.5.2. Congruences

Since is a PID, congruence modulo a non-zero ideal of can be rephrased in terms of congruence modulo a positive integer as follows.

Definition 2.27.

Let . Two integers a and b are said to be congruent modulo n, denoted a ≡ b (mod n), if n|(a – b), that is, if the remainders of Euclidean divisions of a and b by n are the same. In terms of ideals, this is the same as a ≡ b (mod 〈n〉) (See Definition 2.20). Congruence is an equivalence relation on , the equivalence classes being the cosets of the ideal of .

By an abuse of notation, we often denote the equivalence class [a] of simply by a. The following are some basic properties of congruent integers.

Proposition 2.17.

Let , a ≡ b (mod n) and c ≡ d (mod n). Then: a ± c ≡ b ± d (mod n). ac ≡ bd (mod n). For any polynomial , we have f(a) ≡ f(b) (mod n). If n′|n, then a ≡ b (mod n′). If m|a and m|b, then a/m ≡ b/m (mod n/ gcd(n, m)). Proof (1) and (2) follow from the consideration of the quotient ring . (3) follows from repeated applications of (1) and (2). For the proof of (4), consider a – b = kn and n = k′n′ for k, . For proving (5), take a – b = kn = lm. Then m/ gcd(n, m) divides k(n/ gcd(n, m)). Since m/ gcd(n, m) and n/ gcd(n, m) are coprime, by Corollary 2.5 l′ := k/(m/ gcd(n, m)) is an integer and we have a/m – b/m = l = kn/m = l′(n/ gcd(n, m)).

Let with gcd(n_i, n_j) = 1 for i ≠ j. Then lcm(n₁, . . . , n_r) = n₁ · · · n_r, and by the Chinese remainder theorem (Theorem 2.10), we have

This implies that, given integers a₁, . . . , a_r, there exists an integer x unique modulo n₁ · · · n_r such that x satisfies the following congruences simultaneously:

x	≡	a1 (mod n1)
x	≡	a2 (mod n2)
	⋮
x	≡	ar (mod nr)

We now give a procedure for constructing the integer x explicitly. Define N := n₁ · · · n_r and N_i := N/n_i for 1 ≤ i ≤ r. Then for each i we have gcd(n_i, N_i) = 1 and, therefore, there are integers u_i and v_i with u_in_i + v_iN_i = 1. Then (mod N) is the desired solution.

Let . We now study the multiplicative group of the ring . We say that an integer has a multiplicative inverse modulo n, if , or, equivalently, if there is an integer b with ab ≡ 1 (mod n). The following proposition is an important characterization of the elements of .

Proposition 2.18.

(The equivalence class of) an integer a belongs to if and only if gcd(a, n) = 1. Proof [if] By Proposition 2.16, there exist integers u and v such that ua + vn = 1. But then ua ≡ 1 (mod n). [only if] For some integers u and v, we have ua + vn = 1, which implies that the gcd of a and n divides 1 and hence is equal to 1.

Definition 2.28.

The cardinality of is denoted by φ(n). By Proposition 2.18, φ(n) is equal to the number of integers between 0 and n – 1 (both inclusive), which are relatively prime to n. The function is called Euler’s totient function. For example, for a prime p we have , so φ(p) = p – 1.

The following two theorems are immediate consequences of Proposition 2.4.

Theorem 2.14. Euler’s theorem

Let and with gcd(a, n) = 1. Then aφ(n) ≡ 1 (mod n).

Theorem 2.15. Fermat’s little theorem

Let p be a prime and with gcd(a, p) = 1. Then ap–1 ≡ 1 (mod p). For any integer , one has bp ≡ b (mod p).

Theorem 2.16. Wilson’s theorem

For every prime p, we have (p – 1)! ≡ –1 (mod p). Proof The result holds for p = 2. So assume that p is an odd prime. Since is a field, Fermat’s little theorem gives the factorization Equation 2.1 Looking at the constant terms in two sides proves Wilson’s theorem.

The structure of the group , , can be easily deduced from Fermat’s little theorem. This gives us the following important result.

Proposition 2.19.

For a prime p, the group is cyclic. Proof For every divisor d of p –1, we have Xp–1–1 = (Xd–1)f(X) for some with deg f = p – 1 – d. By Congruence 2.1, Xp–1 – 1 has p – 1 roots modulo p. Since is a field, f(X) (mod p) cannot have more than p – 1 – d roots (Proposition 2.25) and it follows that Xd–1 has exactly d roots modulo p. In particular, if d = qe for some and , then there exist exactly qe elements of of orders dividing qe and exactly qe–1 elements of of orders dividing qe–1, that is, there are qe – qe–1 > 0 elements of of order qe. If is the canonical prime factorization of p – 1 (with each ei ≥ 1), by the above argument there exists an element of order for each i = 1, . . . , r. It is now easy to check that has order .

Euler’s totient function plays an extremely important role in number theory (and cryptology). We now describe a method for computing it.

Lemma 2.2.

If n and n′ are relatively prime positive integers, then φ(nn′) = φ(n)φ(n′). Proof If a is invertible modulo nn′, then clearly it is invertible modulo both n and n′. Conversely, if ua ≡ 1 (mod n) and u′a′ ≡ 1 (mod n′), then by the Chinese remainder theorem there are integers x and α, unique modulo nn′, satisfying x ≡ u (mod n), x ≡ u′ (mod n′), α ≡ a (mod n) and α ≡ a′ (mod n′). But then xα ≡ 1 (mod nn′). Therefore, , whence the lemma follows.

Lemma 2.3.

If p is a prime and , then φ(pe) = pe – pe–1 = pe(1 – 1/p). Proof Integers between 0 and pe – 1, which are relatively prime to pe are precisely those that are not multiples of p.

Proposition 2.20.

Let be the prime factorization of a positive integer n with , with pairwise distinct primes p1, . . . , pr and with ei > 0. Then Proof Immediate from Lemmas 2.2 and 2.3.

By Proposition 2.18, the linear congruence ax ≡ 1 (mod n) is solvable for x if and only if gcd(a, n) = 1. In such a case, the solution is unique modulo n. Now, let us concentrate on the solutions of the general linear congruence:

ax ≡ b (mod n).

Theorem 2.17 characterizes the solutions of this congruence.

Theorem 2.17.

Let d := gcd(a, n). Then the congruence ax ≡ b (mod n) is solvable for x if and only if d|b. A solution of the congruence, if existent, is unique modulo n/d. Proof [if] By Proposition 2.17, (a/d)x ≡ b/d (mod n/d). Since gcd(a/d, n/d) = 1, the congruence (a/d)x′ ≡ 1 (mod n/d) is solvable for x′. Then a solution for x is x ≡ (b/d)x′ (mod n/d). [only if] There exists an integer k such that ax + kn = b. This shows that d|b. To prove the uniqueness let x and x′ be two integers satisfying the given congruence. But then a(x – x′) ≡ 0 (mod n), that is, (a/d)(x – x′) ≡ 0 (mod n/d), that is, x – x′ ≡ 0 (mod n/d), since gcd(a/d, n/d) = 1.

The last theorem implies that if d|b, then the congruence ax ≡ b (mod n) has d solutions modulo n. These solutions are given by ξ + r(n/d), r = 0, . . . , d – 1, where ξ is the solution modulo n/d of the congruence (a/d)ξ ≡ b/d (mod n/d).

2.5.3. Quadratic Residues

In this section, we consider quadratic congruences, that is, congruences of the form ax²+bx+c ≡ 0 (mod n). We start with the simple case . We assume further that p is odd, so that 2 has a multiplicative inverse mod p. Since we are considering quadratic equations, we are interested only in those integers a for which gcd(a, p) = 1. In that case, a also has a multiplicative inverse mod p and the above congruence can be written as y² ≡ α (mod p), where y ≡ x + b(2a)^–1 (mod p) and α ≡ b²(4a²)^–1 – c(a^–1) (mod p). This motivates us to provide Definition 2.29.

Definition 2.29.

Let p be an odd prime and a an integer with gcd(a, p) = 1. We say that a is a quadratic residue modulo p, if the congruence x2 ≡ a (mod p) has a solution (for x). Otherwise we say that a is a quadratic non-residue modulo p.

If a is a quadratic residue modulo an odd prime p, then the equation x² ≡ a (mod p) has exactly two solutions. If ξ is one solution, the other solution is p – ξ. It is, therefore, evident that there are exactly (p – 1)/2 quadratic residues and exactly (p – 1)/2 quadratic non-residues modulo p. For example, the quadratic residues modulo p = 11 are 1 = 1² = 10², 3 = 5² = 6², 4 = 2² = 9², 5 = 4² = 7² and 9 = 3² = 8². The quadratic non-residues modulo 11 are, therefore, 2, 6, 7, 8 and 10. We treat 0 neither as a quadratic residue nor as a quadratic non-residue.

Definition 2.30.

Let p be an odd prime and a an integer with gcd(a, p) = 1. The Legendre symbol is defined as:

Proposition 2.21.

Let p be an odd prime and a and b integers coprime to p. Euler’s criterion . . , and . If a ≡ b (mod p), then . In particular, if r is the remainder of Euclidean division of a by p, then . Proof If a is a quadratic residue modulo p, then a ≡ b2 (mod p) for some integer b (coprime to p) and by Fermat’s little theorem we have a(p–1)/2 ≡ bp–1 ≡ 1 (mod p). Conversely, the polynomial Xp–1 – 1 = (X(p–1)/2 – 1)(X(p–1)/2 + 1) has p – 1 (distinct) roots mod p (again by Fermat’s little theorem). We have seen that no quadratic residues are roots of X(p–1)/2 + 1. Since is a field, the (p – 1)/2 roots of X(p–1)/2 – 1 are precisely all the quadratic residues modulo p. This proves Euler’s criterion. The other statements are immediate consequences of this.

Euler’s criterion gives us a nice way to check if a given integer is a quadratic residue modulo an odd prime. While this is much faster than the brute-force strategy of enumerating all the quadratic residues, it is still not the best solution, because it involves a modular exponentiation. We can, however, employ a gcd-like procedure for a faster computation. The development of this method demands further results which are otherwise interesting in themselves as well. The first important result is known as the law of quadratic reciprocity (Theorem 2.18 below). Gauss was the first to prove it and he deemed the result so important that he gave eight proofs for it. At present about two hundred published proofs of this law exist in the literature. We go in the classical way, that is, the Gaussian way, because the proof, though somewhat long, is elementary.

Lemma 2.4. Gauss

Let p be an odd prime and a an integer with gcd(a, p) = 1. Let us denote t := (p – 1)/2. For an integer i, let ri be the unique integer with ri ≡ ia (mod p) and –t ≤ ri ≤ t. Let n be the number of i, 1 ≤ i ≤ t, for which ri is negative. Then . Proof It is easy to check that ri ≢ ±rj (mod p) for all i ≠ j with 1 ≤ i, j ≤ t. Thus |ri|, i = 1, . . . , t, are precisely (a permuted version of) the integers 1, . . . , t. Thus . Canceling t! and using Proposition 2.21(1) gives the desired result.

Definition 2.31.

Let . The largest integer smaller than or equal to x is called the floor of x and is denoted by ⌊x⌋. Similarly, the smallest integer larger than or equal to x is called the ceiling of x and is denoted by ⌈x⌉.

Corollary 2.7.

With the notations of Lemma 2.4 we have (mod 2). If a is odd, then (mod 2). In particular, , that is, 2 is a quadratic residue mod p if and only if p ≡ ±1 (mod 8). Proof Since is even , it follows that if rj > 0, then is even, and if rj < 0, then is odd. Therefore, (mod 2). If a is odd, p + a is even. Also 4 is a quadratic residue modulo p. So , where (mod 2) and (mod 2). Putting a = 1 gives and, therefore, , that is, .

Theorem 2.18. Law of quadratic reciprocity

Let p and q be distinct odd primes. Then . Proof By Corollary 2.7, , where , , s = (q – 1)/2 and t = (p – 1)/2. So we are done, if we can show that m + n = st. Consider the set S := {(x, y) | 1 ≤ x ≤ s, 1 ≤ y ≤ t} of cardinality st. Now S is the disjoint union of S1 and S2, where and . (Note that we cannot have px = qy.) It is easy to see that #S1 = m and #S2 = n.

To demonstrate how we can use the results deduced so far, let us compute . Since 360 = 2³ · 3² · 5, we have

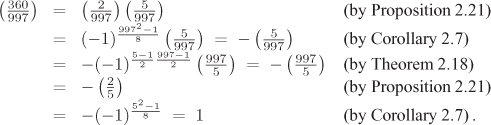
Thus 360 is a quadratic residue modulo 997. The apparent attractiveness of this method is beset by the fact that it demands the factorization of several integers and as such does not lead to a practical algorithm. We indeed need further machinery in order to have an efficient algorithm. First, we define a generalization of the Legendre symbol.

Definition 2.32.

Let a, b be integers with b > 0 and odd. We define the Jacobi symbol as where, in the last case, p1, . . . , pt are all the prime factors of b (not necessarily all distinct).

Note that if , then a is not a quadratic residue mod b. However, the converse is not always true, that is, does not necessarily imply that a is a quadratic residue modulo b (Example: a = 2 and b = 9). Of course, if b is an odd prime and if gcd(a, b) = 1, the Legendre and Jacobi symbols correspond to the same value and meaning.

The Jacobi symbol enjoys many properties similar to the Legendre symbol.

Proposition 2.22.

For integers a, a′ and positive odd integers b, b′, we have: , , and if a ≡ a′ (mod b), then . In particular, if r is the remainder of Euclidean division of a by b, then . Proof Immediate from the definition and Proposition 2.21.

Theorem 2.19.

For an odd positive integer b If a is another odd positive integer with gcd(a, b) = 1, then Proof Let b = p1 · · · ps, where pi are odd primes (not necessarily distinct). Then by definition , where . Now for odd integers x and y one has (mod 2). Repeated applications of this prove that (mod 2). To prove that , we proceed in a similar manner and note that for odd integers x and y one has (mod 2). If with odd primes, then by definition where from Theorem 2.18 it follows that

Now, we can calculate without factoring as follows.

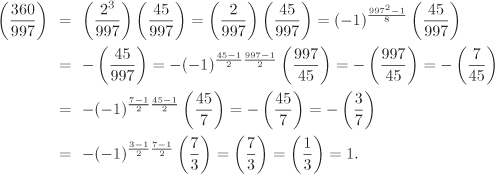
2.5.4. Some Assorted Topics

So far, we have studied some elementary properties of integers. Number theory is, however, one of the oldest and widest branches of mathematics. Various complex-analytic and algebraic tools have been employed to derive more complicated properties of integers. In Section 2.13, we give a short introductory exposition to algebraic number theory. Here, we mention a collection of useful results from analytic number theory. The proofs of these analytic results would lead us too far away and hence are omitted here. Inquisitive (and/or cynical) readers may consult textbooks on analytic number theory for the details missing here.

The prime number theorem

The famous prime number theorem gives an asymptotic estimate of the density of primes smaller than or equal to a positive real number. Gauss conjectured this result in 1791. Many mathematicians tried to prove it during the 19^th century and came up with partial results. Riemann made reasonable progress towards proving the theorem, but could not furnish a complete proof before he died in 1866. It is interesting to mention here that a good portion of the theory of analytic functions (also called holomorphic functions) in complex analysis was developed during these attempts to prove the prime number theorem. The first complete proof of the theorem (based mostly on the ideas of Riemann and Chebyshev) was given independently by the French mathematician Hadamard and by the Belgian mathematician de la Vallée Poussin in 1896. Their proof is regarded as one of the major achievements of modern mathematics. People started believing that any proof of the prime number theorem has to be analytic. Erdös and Selberg destroyed this belief by independently providing the first elementary proof of the theorem in 1949. Here (and elsewhere in mathematics), the adjective elementary refers to something which does not depend on results from analysis or algebra. Caution: Elementary is not synonymous with easy !

Theorem 2.20. Prime Number Theorem

Let π(x) denote the number of primes less than or equal to a real number x > 0. As x → ∞ we have π(x) → x/ln x (that is, the ratio π(x)/(x/ln x) → 1). In particular, for the density π(n)/n of primes among the natural numbers ≤ n asymptotically approaches 1/ ln n as n → ∞. It also follows that the n-th prime is approximately equal to n ln n.

Though the prime number theorem provides an asymptotic estimate (that is, one for x → ∞), for finite values of x (for example, for the values of x in the cryptographic range) it does give good approximations for π(x). Table 2.1 lists π(x) against the rounded values of x/ ln x for x equal to small powers of 10.

Table 2.1. Approximations to π(x)

x	π(x)	x/ ln x	x/(ln x – 1)	Li(x)
103	168	145	169	178
104	1229	1086	1218	1246
105	9592	8686	9512	9630
106	78,498	72,382	78,030	78,628
107	664,579	620,421	661,458	664,918
108	5,761,455	5,428,681	5,740,304	5,762,209

Given the prime number theorem it follows that π(x) approaches x/(ln x – ξ) for any real ξ. It turns out that ξ = 1 is the best choice. Gauss’ Li function is also an asymptotic estimate for π(x), where for real x > 0 one defines:

Gauss conjectured that Li(x) asymptotically equals π(x). The prime number theorem is, in fact, equivalent to this conjecture. Furthermore, de la Vallée Poussin proved that Li(x) is a better approximation to π(x) than x/(ln x – ξ) for any real ξ. Table 2.1 also lists x/(ln x – 1) and Li(x) against the actual values of π(x).

The asymptotic formula does not rule out the possibility that the error π(x)–(x/ ln x) tends to zero as x → ∞. It has been shown by Dusart [83] that (x/ ln x) – 0.992(x/ ln² x) ≤ π(x) ≤ (x/ ln x) + 1.2762(x/ ln² x) for all x > 598.

Density of smooth integers

Integers having only small prime divisors play an interesting role in cryptography and in number theory in general.

Definition 2.33.

Let . An integer x is called y-smooth (or simply smooth, if y is understood from the context), if all the prime divisors of x are ≤ y. We denote by ψ(x, y) the fraction of positive integers ≤ x, that are y-smooth.

The following theorem gives an asymptotic estimate for ψ(x, y).

Theorem 2.21.

Let x, with x > y and let u := ln x/ ln y. For u → ∞ and y ≥ ln2 x we have the asymptotic formula: ψ(x, y) → u–u+o(u) = e–[(1+o(1))u ln u].

In Theorem 2.21, the notation g(u) = o(f(u)) implies that the ratio g(u)/f(u) tends to 0 as u approaches ∞. See Definition 3.1 for more details. An interesting special case of the formula for ψ(x, y) will be used quite often in this book and is given as Corollary 4.1 in Chapter 4.

Like the prime number theorem, Theorem 2.21 gives only asymptotic estimates, but is indeed a good approximation for finite values of x, y and u (that is, for the values of practical interest). The most important implication of this theorem is that the density of y-smooth integers in the set {1, . . . , x} is a very sensitive function of u = ln x/ ln y and decreases very rapidly as x increases. For example, if y = 15,485,863, the millionth prime, then a random integer ≤ 2²⁵⁰ is y-smooth with probability approximately 2.12 × 10^–11, whereas a random integer ≤ 2⁵⁰⁰ is y-smooth with probability approximately 2.23 × 10^–28. (These figures are computed neglecting the o(u) term in the expression of ψ(x, y).) In other words, smaller integers have higher probability of being smooth (that is, y-smooth for a given y).

The extended Riemann hypothesis

The Riemann hypothesis (RH) is one of the deepest unsolved problems in mathematics. An extended version of this hypothesis has important bearings on the solvability of certain computational problems in polynomial time.

Definition 2.34.

The Euler zeta function ζ(s) is defined for a complex variable s with Re s ≥ 1 as The reader may already be familiar with the results: ζ(1) = ∞, ζ(2) = π2/6 and ζ(4) = π4/90. Riemann (analytically) extended the Euler Zeta function for all complex values of s (except at s = 1, where the function has a simple pole). This extended function, called the Riemann zeta function, is known to have zeros at s = –2, –4, –6, . . . . These are called the trivial zeros of ζ(s). It can be proved that all non-trivial zeros of ζ(s) must lie in the so-called critical strip : 0 ≤ Re s ≤ 1, and are symmetric about the critical line: Re s = 1/2.

Conjecture 2.1. Riemann hypothesis (RH)

All non-trivial zeros of ζ(s) lie on the critical line.

In 1900, Hilbert asserted that proving or disproving the RH is one of the most important problems confronting 20^th century mathematicians. The problem continues to remain so even to the 21^st century mathematicians.

In 1901, von Koch proved that the RH is equivalent to the formula:

Conjecture 2.2. An equivalent form of the Riemann hypothesis

π(x) = Li(x) + O(x1/2 ln x)

Here the order notation f(x) = O(g(x)) means that |f(x)/g(x)| is less than a constant for all sufficiently large x (See Definition 3.1).

Hadamard and de la Vallée Poussin proved that

for some positive constant α. While this estimate was sufficient to prove the prime number theorem, the tighter bound of Conjecture 2.2 continues to remain unproved.

Theorem 2.22. Dirichlet’s theorem on primes in arithmetic progression

Let a, be coprime. The set contains an infinite number of primes.

Dirichlet’s theorem is a powerful generalization of Theorem 2.12 (which corresponds to a = b = 1). One can accordingly generalize the notation π(x) as follows:

Definition 2.35.

Let a, with gcd(a, b) = 1. By πa, b(x), we denote the number of primes in the set , that are ≤ x.

The prime number theorem gives the estimate:

where φ is Euler’s totient function. The RH now generalizes to:

Conjecture 2.3. Extended Riemann hypothesis (ERH)

For a, with gcd(a, b) = 1,

Some authors use the expression Generalized Riemann hypothesis (GRH) in place of ERH. Taking b = 1 demonstrates that the ERH implies the RH. The ERH also implies the following:

Conjecture 2.4.

The smallest positive quadratic non-residue modulo a prime p is < 2 ln2 p.

Exercise Set 2.5

2.35	Show that any integer n ≥ 3 satisfies n2 = a2 – b2 for some a, . Show that for any integer n ≥ 2 the integer n4 + 4n is composite.
2.36	Let and S a subset of {1, 2, ..., 2n} of cardinality n + 1. Show that: [H] There exist x, such that x – y = 1. There exist x, such that x – y = n. There exist distinct x, such that x is a multiple of y. There exist distinct x, such that x is relatively prime to y.
2.37	Show that for any , n > 1, the rational number is not an integer. [H]
2.38	Show that the Mersenne number Mn := 2n – 1 is prime only if n is prime. Show that the Fermat number 2n + 1 is prime only if n = 2t for some .
2.39	Let n ≥ 2 be a natural number. A complete residue system modulo n is a set of n integers a1, . . . , an such that ai ≢ aj (mod n) for i ≠ j. Similarly, a reduced residue system modulo n is a set of φ(n) integers b1, . . . , bφ(n) such that gcd(bi, n) = 1 for all i = 1, . . . , φ(n) and bi ≢ bj (mod n) for i ≠ j. Show that: If {a1, . . . , an} is a complete residue system modulo n, the equivalence classes of a1, . . . , an (modulo the ideal ) constitute the set . In other words, given any integer a, there exists a unique i, 1 ≤ i ≤ n, for which a ≡ ai (mod n). If {b1, . . . , bφ(n)} is a reduced residue system modulo n, then the equivalence classes of b1, . . . , bφ(n) constitute the set . In other words, given any integer b coprime to n, there exists a unique i, 1 ≤ i ≤ φ(n), for which b ≡ bi (mod n). If {a1, . . . , an} is a complete residue system modulo n, then for any integer a coprime to n, the integers aa1, . . . , aan constitute a complete residue system modulo n. For example, if n is odd, then {2, 4, 6, . . . , 2n} is a complete residue system modulo n. If {b1, . . . , bφ(n)} is a reduced residue system modulo n, then for any integer b coprime to n, the integers bb1, . . . , bbφ(n) constitute a reduced residue system modulo n. For n > 2, the integers 12, 22, . . . , n2 do not constitute a complete residue system modulo n. [H] If p is an odd prime and if {a1, . . . , ap} and are two complete residue systems modulo p, then is not a complete residue system modulo p. [H]
2.40	Prove that the decimal expansion of any rational number a/b is recurring, that is, (eventually) periodic. (A terminating expansion may be viewed as one with recurring 0.) [H]
2.41	Let p be an odd prime. Show that the congruence x2 ≡ –1 (mod p) is solvable if and only if p ≡ 1 (mod 4). [H]
2.42	Let . Show that if n > 2, then φ(n) is even. Show that if n is odd, then φ(n) = φ(2n). Find out all the values of n for which φ(n) = 12.
2.43	For , show that .
2.44	Let n > 2 and gcd(a, n) = 1. Let h be the multiplicative order of a modulo n (that is, in the group ). Show that: ai ≡ aj (mod n) if and only if i ≡ j (mod h). The multiplicative order of al modulo n is h/ gcd(h, l). If a is a primitive element of (that is, if h = φ(n)), then 1, a, a2, . . . , ah–1 is a reduced residue system modulo n. If gcd(b, n) = 1 and b has multiplicative order k modulo n and if gcd(h, k) = 1, then the multiplicative order of ab modulo n is hk.
2.45	Device a criterion for the solvability of ax2 + bx + c ≡ 0 (mod p), where p is an odd prime and gcd(a, p) = 1. [H]
2.46	Let p be a prime and . An integer a with gcd(a, p) = 1 is called an r-th power residue modulo p, if the congruence xr ≡ a (mod p) has a solution. Show that a is an r-th power residue modulo p if and only if a(p–1)/ gcd(r, p–1) ≡ 1 (mod p). This is a generalization of Euler’s criterion for quadratic residues.
2.47	Let G be a finite cyclic group of cardinality n. Show that and that there are exactly φ(n) generators (that is, primitive elements) of G.
2.48	Let m, with m|n. Show that the canonical (surjective) ring homomorphism induces a surjective group homomorphism of the respective groups of units. (Note that every ring homomorphism induces a group homomorphism , where A* and B* are the groups of units of A and B respectively. Even when is surjective, need not be surjective, in general. As an example consider the canonical surjection for a prime p > 3.)
2.49	In this exercise, we investigate which of the groups is cyclic for a prime p and . Show that and are cyclic, but is not cyclic. Conclude that is not cyclic for e ≥ 3. [H] More specifically, show that for e ≥ 3 the multiplicative group is the direct product of two cyclic subgroups generated by –1 and 5 respectively. Show that if p is an odd prime and , then is cyclic. [H]
2.50	Show that the multiplicative group , n ≥ 2, is cyclic if and only if n = 2, 4, pe, 2pe, where p is an odd prime and . [H]