**2.14. p-adic Numbers
Let us now study a different area of algebraic number theory, introduced by Kurt Hensel in an attempt to apply power series expansions in connection with numbers. While trying to explain the properties of (rational) integers mathematicians started embedding ![]() in bigger and bigger structures, richer and richer in properties.
in bigger and bigger structures, richer and richer in properties. ![]() came in a natural attempt to form quotients, and for some time people believed that that is all about reality. Pythagoras was seemingly the first to locate and prove the irrationality of a number, namely,
came in a natural attempt to form quotients, and for some time people believed that that is all about reality. Pythagoras was seemingly the first to locate and prove the irrationality of a number, namely, ![]() . It took humankind centuries for completing the picture of the real line. One possibility is to look
. It took humankind centuries for completing the picture of the real line. One possibility is to look ![]() as the completion of
as the completion of ![]() . A sequence an,
. A sequence an, ![]() , of rational numbers is called a Cauchy sequence if for every real ε > 0, there exists
, of rational numbers is called a Cauchy sequence if for every real ε > 0, there exists ![]() such that |am – an| ≤ ε for all m,
such that |am – an| ≤ ε for all m, ![]() , m, n ≥ N. Every Cauchy sequence should converge to a limit and it is
, m, n ≥ N. Every Cauchy sequence should converge to a limit and it is ![]() (and not
(and not ![]() ) where this happens. Seeing convergence of Cauchy sequences, people were not wholeheartedly happy, because the real polynomial X2 + 1 did not have—it continues not to have—roots in
) where this happens. Seeing convergence of Cauchy sequences, people were not wholeheartedly happy, because the real polynomial X2 + 1 did not have—it continues not to have—roots in ![]() . So the next question that arose was that of algebraic closure.
. So the next question that arose was that of algebraic closure. ![]() was invented and turned out to be a nice field which is both algebraically closed and complete.
was invented and turned out to be a nice field which is both algebraically closed and complete.
Throughout the above business, we were led by the conventional notion of distance between points (that is, between numbers)—the so-called Archimedean distance or the absolute value. For every rational prime p, there exists a p-adic distance which leads to a ring ![]() strictly bigger than and containing
strictly bigger than and containing ![]() . This is the ring of p-adic integers. The quotient field of
. This is the ring of p-adic integers. The quotient field of ![]() is the field
is the field ![]() of p-adic numbers.
of p-adic numbers. ![]() is complete in the sense of convergence of Cauchy sequences (under the p-adic distance), but is not algebraically closed. We know anyway that a (unique) algebraic closure
is complete in the sense of convergence of Cauchy sequences (under the p-adic distance), but is not algebraically closed. We know anyway that a (unique) algebraic closure ![]() of
of ![]() exists. We have
exists. We have ![]() , that is, it was necessary and sufficient to add the imaginary quantity i to
, that is, it was necessary and sufficient to add the imaginary quantity i to ![]() to get an algebraically closed field. Unfortunately in the case of the p-adic distance the closure
to get an algebraically closed field. Unfortunately in the case of the p-adic distance the closure ![]() is of infinite extension degree over
is of infinite extension degree over ![]() . In addition,
. In addition, ![]() is not complete. An attempt to make
is not complete. An attempt to make ![]() complete gives an even bigger field Ωp and the story stops here, Ωp being both algebraically closed and complete. But Ωp is already a pretty huge field and very little is known about it.
complete gives an even bigger field Ωp and the story stops here, Ωp being both algebraically closed and complete. But Ωp is already a pretty huge field and very little is known about it.
In the rest of this section, we, without specific mention, denote by p an arbitrary rational prime.
2.14.1. The Arithmetic of p-adic Numbers
There are various ways in which p-adic integers can be defined. A simple way is to use infinite sequences.
Definition 2.111.
|
A p-adic integer is defined as an infinite sequence
|
See Exercise 2.144 for another way of defining p-adic integers. We now show that ![]() is a ring. Before doing that, we mention that the ring
is a ring. Before doing that, we mention that the ring ![]() is canonically embedded in
is canonically embedded in ![]() by the injective map
by the injective map ![]() , a ↦ (a).
, a ↦ (a).
Definition 2.112.
It turns out that ![]() is an integral domain. In order to see why, let us focus our attention on the units of
is an integral domain. In order to see why, let us focus our attention on the units of ![]() . Let us plan to denote
. Let us plan to denote ![]() (the multiplicative group of units of
(the multiplicative group of units of ![]() ) by Up. The next result characterizes elements of Up.
) by Up. The next result characterizes elements of Up.
Proposition 2.52.
|
For
Proof [(a)⇒(b)] Let (an)(bn) = (anbn) = 1 = (1) for some [(b)⇒(c)] Obvious. [(c)⇒(a)] Let us construct a p-coherent sequence bn, We also have an+1bn+1 ≡ 1 (mod pn), that is, anbn+1 ≡ 1 (mod pn), that is, |
Proposition 2.53.
|
Every Proof If p a1, take r := 0 and y := x. So assume that p|a1. Choose |
Proposition 2.54.
|
Proof Let x1 and x2 be non-zero elements of |
Definition 2.113.
|
The quotient field |
Proposition 2.55.
|
Every non-zero Proof One can write x = a/b for some a, |
The canonical inclusion ![]() naturally extends to the canonical inclusion
naturally extends to the canonical inclusion ![]() . We can identify
. We can identify ![]() with the rational a/b and say that
with the rational a/b and say that ![]() is contained in
is contained in ![]() . Being a field of characteristic 0,
. Being a field of characteristic 0, ![]() contains an isomorphic copy of
contains an isomorphic copy of ![]() . The map
. The map ![]() gives this isomorphism explicitly. Note that the ring
gives this isomorphism explicitly. Note that the ring ![]() is strictly bigger than
is strictly bigger than ![]() and the field
and the field ![]() is strictly bigger than the field
is strictly bigger than the field ![]() (Exercise 2.147).
(Exercise 2.147).
2.14.2. The p-adic Valuation
Proposition 2.55 leads to the notion of p-adic distance between pairs of points in ![]() . Let us start with some formal definitions.
. Let us start with some formal definitions.
Definition 2.114.
|
A metric on a set S is a map
A set S together with a metric d is called a metric space (with metric d). |
Definition 2.115.
|
A norm on a field K is a map
It is an easy check that for a norm ‖ ‖ on K the function A norm ‖ ‖ on a field K is called non-Archimedean (or a finite valuation), if ‖x + y‖ ≤ max(‖x‖, ‖y‖) for all x, |
Example 2.34.
|
Definition 2.116.
|
The p-adic norm
|
Theorem 2.59.
|
The p-adic norm | |p is a non-Archimedean norm on Proof Non-negative-ness, non-degeneracy and multiplicativity of | |p are immediate. For proving the triangle inequality, it is sufficient to prove the non-Archimedean condition. Take x, |
Definition 2.117.
|
Two metrics d1 and d2 on a metric space S are called equivalent if a sequence (xn) from S is Cauchy with respect to d1 if and only if it is Cauchy with respect to d2. Two norms on a field are called equivalent if they induce equivalent metrics. |
For every ![]() , the field
, the field ![]() is canonically embedded in
is canonically embedded in ![]() and thus we have a notion of a p-adic distance on
and thus we have a notion of a p-adic distance on ![]() . We also have the usual Archimedean distance | |∞ on
. We also have the usual Archimedean distance | |∞ on ![]() . We now state an interesting result without a proof, which asserts that any distance on
. We now state an interesting result without a proof, which asserts that any distance on ![]() must be essentially the same as either the usual Archimedean distance or one of the p-adic distances.
must be essentially the same as either the usual Archimedean distance or one of the p-adic distances.
Theorem 2.60. Ostrowski’s theorem
The notions of sequences and series and their convergences can be readily extended to ![]() under the norm | |p. Since the p-adic distance assumes only the discrete values pr,
under the norm | |p. Since the p-adic distance assumes only the discrete values pr, ![]() , it is often customary to restrict ourselves only to these values while talking about the convergence criteria of sequences and series, that is, instead of an infinitesimally small real ε > 0 one can talk about an arbitrarily large
, it is often customary to restrict ourselves only to these values while talking about the convergence criteria of sequences and series, that is, instead of an infinitesimally small real ε > 0 one can talk about an arbitrarily large ![]() with p–M ≤ ε.
with p–M ≤ ε.
Definition 2.118.
|
Let x1, x2, . . . be a sequence of elements of Consider the partial sums A sequence x1, x2, . . . of elements of |
Definition 2.119.
|
A field K is called complete under a norm ‖ ‖ if every sequence of elements of K, which is Cauchy under ‖ ‖, converges to an element in K. |
For example, ![]() is complete under | |∞. We shortly demonstrate that
is complete under | |∞. We shortly demonstrate that ![]() is complete under | |p.
is complete under | |p.
Consider a field K not (necessarily) complete under a norm ‖ ‖. Let C denote the set of all Cauchy sequences ![]() from K. Define addition and multiplication in C as (an) + (bn) := (an + bn) and (an)(bn) := (anbn). Under these operations C becomes a commutative ring with identity having a maximal ideal
from K. Define addition and multiplication in C as (an) + (bn) := (an + bn) and (an)(bn) := (anbn). Under these operations C becomes a commutative ring with identity having a maximal ideal ![]() . The field
. The field ![]() is called the completion of K with respect to the norm ‖ ‖. K is canonically embedded in L via the map
is called the completion of K with respect to the norm ‖ ‖. K is canonically embedded in L via the map ![]() . The norm ‖ ‖ on K extends to elements
. The norm ‖ ‖ on K extends to elements ![]() of L as limn→∞ ‖an‖. L is a complete field under this extended norm. In fact, it is the smallest field containing K and complete under ‖ ‖.
of L as limn→∞ ‖an‖. L is a complete field under this extended norm. In fact, it is the smallest field containing K and complete under ‖ ‖.
![]() is the completion of
is the completion of ![]() with respect to the Archimedean norm | |∞. On the other hand,
with respect to the Archimedean norm | |∞. On the other hand, ![]() turns out to be the completion of
turns out to be the completion of ![]() with respect to the p-adic norm | |p. Before proving this let us first prove that
with respect to the p-adic norm | |p. Before proving this let us first prove that ![]() itself is a complete field under the p-adic norm. Let us start with a lemma.
itself is a complete field under the p-adic norm. Let us start with a lemma.
Lemma 2.18.
|
A sequence (an) of p-adic numbers is a Cauchy sequence if and only if the sequence (an+1 – an) converges to 0. Proof [if] Take any Thus (an) is a Cauchy sequence. [only if] Take any |
Theorem 2.61.
|
The field Proof Let (an) be a Cauchy sequence in
It then follows that |an|p ≤ p–m for all Let an = an,0+an,1p+an,2p2+· · · be the p-adic expansion of an (Exercise 2.145). Since (an) is Cauchy, for every |
Theorem 2.62.
|
Proof Let C denote the ring of Cauchy sequences from If What remains is to show that the map |
Corollary 2.29.
|
The p-adic series Proof The only if part is obvious. For the if part, take a sequence (an) of p-adic numbers with |an|p → 0. Define |
This is quite unlike the Archimedean norm | |∞. For example, with respect to this norm ![]() , whereas the series
, whereas the series ![]() diverges.
diverges.
2.14.3. Hensel’s Lemma
Let us conclude our short study of p-adic methods by proving an important theorem due to Hensel. This theorem talks about the solvability of polynomial equations f(X) = 0 for ![]() . Before proceeding further, let us introduce a notation. Recall that every
. Before proceeding further, let us introduce a notation. Recall that every ![]() has a unique p-adic expansion of the form a = a0 + a1p + a2p2 + · · · with 0 ≤ an < p (Exercises 2.144 and 2.145). If a0 = a1 = · · · = an–1 = 0, then a = anpn + an+1pn+1 + an +2pn+2 + · · · = pnb, where
has a unique p-adic expansion of the form a = a0 + a1p + a2p2 + · · · with 0 ≤ an < p (Exercises 2.144 and 2.145). If a0 = a1 = · · · = an–1 = 0, then a = anpn + an+1pn+1 + an +2pn+2 + · · · = pnb, where ![]() . Thus pn|a in
. Thus pn|a in ![]() . We denote this by saying that a ≡ 0 (mod pn). Notice that a ≡ 0 (mod pn) if and only if |a|p ≤ p–n. We write a ≡ b (mod pn) for a,
. We denote this by saying that a ≡ 0 (mod pn). Notice that a ≡ 0 (mod pn) if and only if |a|p ≤ p–n. We write a ≡ b (mod pn) for a, ![]() , if a – b ≡ 0 (mod pn). Since pn can be viewed as the element
, if a – b ≡ 0 (mod pn). Since pn can be viewed as the element ![]() of
of ![]() , this congruence notation conforms to that for a general PID. (
, this congruence notation conforms to that for a general PID. (![]() is a PID by Exercise 2.148.)
is a PID by Exercise 2.148.)
Since by our assumption any ring A comes with identity (that we denote by 1 = 1A), it makes sense to talk for every ![]() about an element n = nA in A, which is the n-fold sum of 1. More precisely:
about an element n = nA in A, which is the n-fold sum of 1. More precisely:
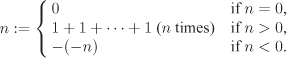
Given any ![]() , one can define the formal derivative of f as
, one can define the formal derivative of f as ![]() . Properties of formal derivatives of polynomials are covered in Exercise 2.61.
. Properties of formal derivatives of polynomials are covered in Exercise 2.61.
Theorem 2.63. Hensel’s lemma
|
Let
Then there exists a unique Proof Let us inductively construct a sequence α0, α1, α2, · · · of p-adic integers with the properties that |f(αn)|p ≤ p–(2M+n+1) and |f′(αn)|p = p–M for every
We want to find a suitable kn for which |f(αn)|p ≤ p–(2M+n+1). Taylor expansion gives f(αn) = f(αn–1) + knpM+nf′(αn–1) + cnp2(M+n) for some
Since pM+1 f′(αn–1), the element
This value of kn yields f (αn) = p2M + n(bnp + cnpn) ≡ 0 (mod p2M+n+1) for some Since |αn – αn–1|p ≤ p–(M+n), it follows that αn – αn–1 → 0, that is, (αn) is a Cauchy sequence (under | |p). By the completeness of For proving the uniqueness of α, let |
Note that αn in the last proof satisfies the congruence
f(αn) ≡ 0 (mod p2M+n+1)
for each ![]() . We are given the solution α0 corresponding to n = 0. From this, we inductively construct the solutions α1, α2, . . . corresponding to n = 1, 2, . . . respectively. The process for computing αn from αn–1 as described in the proof of Hensel’s lemma is referred to as Hensel lifting. The given conditions ensure that this lifting is possible (and uniquely doable) for every
. We are given the solution α0 corresponding to n = 0. From this, we inductively construct the solutions α1, α2, . . . corresponding to n = 1, 2, . . . respectively. The process for computing αn from αn–1 as described in the proof of Hensel’s lemma is referred to as Hensel lifting. The given conditions ensure that this lifting is possible (and uniquely doable) for every ![]() , and in the limit n → ∞ we get a root
, and in the limit n → ∞ we get a root ![]() of f. Since each kn is required modulo p, we can take
of f. Since each kn is required modulo p, we can take ![]() . So α admits a p-adic expansion of the form α = α0 + k1pM+1 + k2pM+2 + k3pM+3 + · · ·.
. So α admits a p-adic expansion of the form α = α0 + k1pM+1 + k2pM+2 + k3pM+3 + · · ·.
The special case M = 0 for Hensel’s lemma is now singled out:
Corollary 2.30.
|
Let
Then there exists a unique |
For this special case, we compute solutions αn of f(x) ≡ 0 (mod pn+1) inductively for n = 1, 2, 3, . . . , given a suitable solution α0 of this congruence for n = 0. The lifting formula is now:
Equation 2.21
![]()
Example 2.35.
|
For example, let p be an odd prime and As a specific numerical example, take p = 7, a = 2 and α0 = 3. Using Formula (2.21), we compute k1 = 1, α1 = 10, k2 = 2, α2 = 108, k3 = 6, α3 = 2166, and so on. Thus a square root of 2 in |
Exercise Set 2.14
| 2.144 |
|
| 2.145 | In view of Exercise 2.144, every
|
| 2.146 | Let p be an odd prime and |
| 2.147 |
|
| 2.148 | Prove the following assertions:
|
| 2.149 | Compute the p-adic expansion of 1/3 in |
| 2.150 | Show that |
| 2.151 | Prove the following assertions that establish that
|
| 2.152 | Show that:
|
| 2.153 | Prove that |
| 2.154 | Prove that for any |
| 2.155 | Let p, |
| 2.156 | Let a be an integer congruent to 1 modulo 8. Show that there exists an |
| 2.157 | Compute |
| 2.158 | Let p be an odd prime and |
| 2.159 | Show that the polynomial X2 – p is irreducible in |
| 2.160 | Teichmüller representative Let |
| 2.161 | Show that the algebraic closure |

 .
.