2.3. Groups
So far we have studied sets as unordered collections. However things start getting interesting if we define one or more binary operations on sets. Such operations define structures on sets and we compare different sets in light of their respective structures. Groups are the first (and simplest) examples of sets with binary operations.
Definition 2.1.
|
A binary operation on a set A is a map from A × A to A. If ◊ is a binary operation on A, it is customary to write a ◊ a′ to denote the image of (a, a′) (under ◊).
|
For example, addition, subtraction and multiplication are all binary operations on 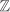 (or
(or 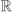 or
or 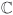 ). Subtraction is not a binary operation on
). Subtraction is not a binary operation on  , since, for example, 2 – 3 is not an element of
, since, for example, 2 – 3 is not an element of  . Division is not a binary operation on
. Division is not a binary operation on 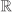 , since division by zero is not defined. Division is a binary operation on
, since division by zero is not defined. Division is a binary operation on  .
.
2.3.1. Definition and Basic Properties
Definition 2.2.
|
A group (G, ◊) is a set G together with a binary operation ◊ on G, that satisfy the following three conditions:
Associativity (a ◊ b) ◊ c = a ◊ (b ◊ c) for all a, b, 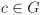 . . Identity element There exists a (unique) element 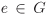 such that e ◊ a = a ◊ e = a for all such that e ◊ a = a ◊ e = a for all 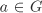 . The element e is called the identity of G. . The element e is called the identity of G. Inverse For each 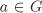 , there exists a (unique) element , there exists a (unique) element  such that a ◊ b = b ◊ a = e. The element b is called the inverse of a. such that a ◊ b = b ◊ a = e. The element b is called the inverse of a. If, in addition, we assume that Commutativity a ◊ b = b ◊ a for all a,  , , then G is called a commutative or an Abelian group.
|
A group (G, ◊) is also written in short as G, when the operation ◊ is understood from the context. More often than not, the operation ◊ is either addition (+) or multiplication (·) in which cases we also say that G is respectively an additive or a multiplicative group. For a multiplicative group, we often omit the multiplication sign and denote a · b simply as ab. The identity in an additive group is usually denoted by 0, whereas that in a multiplicative group by 1. The inverse of an element a in these cases are denoted respectively by –a and a–1. Groups written additively are usually Abelian, but groups written multiplicatively need not be so.
Note that associativity allows us to write a ◊ b ◊ c unambiguously to represent (a ◊ b) ◊ c = a ◊ (b ◊ c). More generally, if  , then a1 ◊ ··· ◊ an represents a unique element of the group irrespective of how we insert brackets to compute the element a1 ◊ ··· ◊ an.
, then a1 ◊ ··· ◊ an represents a unique element of the group irrespective of how we insert brackets to compute the element a1 ◊ ··· ◊ an.
Example 2.1.
The set 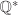 of non-zero rational numbers is a group under multiplication. The identity is 1 = 1/1 and the inverse of a/b is b/a. of non-zero rational numbers is a group under multiplication. The identity is 1 = 1/1 and the inverse of a/b is b/a. For a set A, the set of all bijective functions A → A is a group under composition of functions. The identity element is idA and the inverse of f is denoted by f–1. (See also Exercise 2.2.) This group is not Abelian in general. A group G is called finite, if G as a set consists of (only) finitely many elements. Finite groups play an extremely important role in cryptography. Here is our first example of finite groups: Let n be an integer ≥ 2. The set
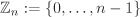
is a group under addition modulo n (that is, add (and subtract) two elements in 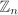 as integers and if the result is not in as integers and if the result is not in 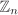 , take the remainder of division by n). For this group, the identity element is 0 and –a = n – a for a ≠ 0 and –0 = 0. (See Example 2.3 for a formal definition of , take the remainder of division by n). For this group, the identity element is 0 and –a = n – a for a ≠ 0 and –0 = 0. (See Example 2.3 for a formal definition of 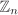 .) .) For an integer n ≥ 2, define the set
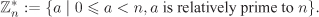
If n is prime, then  . The set . The set 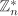 is a group under multiplication modulo n with identity 1. We need little more machinery than introduced so far in order to prove that every element is a group under multiplication modulo n with identity 1. We need little more machinery than introduced so far in order to prove that every element 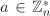 has a multiplicative inverse modulo n. Other group axioms are easy to check. has a multiplicative inverse modulo n. Other group axioms are easy to check.
|
Proposition 2.1.
|
Let (G, ◊) be a group and let a, b, 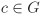 . Then a ◊ b = a ◊ c implies b = c. Similarly, a ◊ c = b ◊ c implies a = b. These statements are commonly known as (left and right) cancellation laws. . Then a ◊ b = a ◊ c implies b = c. Similarly, a ◊ c = b ◊ c implies a = b. These statements are commonly known as (left and right) cancellation laws.
Proof
We prove only the left cancellation law. The proof of the other law is similar. Let e denote the identity of G and d the inverse of a. Then b = e ◊ b = (d ◊ a) ◊ b = d ◊ (a ◊ b) = d ◊ (a ◊ c) = (d ◊ a) ◊ c = e ◊ c = c.
|
2.3.2. Subgroups, Cosets and Quotient Groups
Definition 2.3.
|
Let (G, ◊) be a group. Then a subset H of G is called a subgroup of G, if H is a group under the operation ◊ inherited from G. For a subset H of G to be a subgroup, it is necessary and sufficient that H is closed under the operation ◊ and under inverse. Any subgroup of an Abelian group is also Abelian.
|
Example 2.2.
For any group G with identity element e, the subsets {e} and G are subgroups of G. They are called the trivial subgroups of G. For an integer n ≥ 2, the set of all integral multiples of n is an additive subgroup of 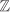 and is denoted by and is denoted by 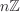 . . The set 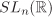 consisting of all n × n real matrices of determinant 1 is a subgroup of consisting of all n × n real matrices of determinant 1 is a subgroup of 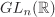 and is commonly referred to as the special linear group. and is commonly referred to as the special linear group.
|
Let (G, ◊) be a group. For subsets A and B of G, we denote by A ◊ B the set  . In particular, if A = {a} (resp. B = {b}), then A ◊ B is denoted by a ◊ B (resp. A ◊ b). Note that the sets A ◊ B and B ◊ A are not necessarily equal. If G is Abelian, then A ◊ B = B ◊ A.
. In particular, if A = {a} (resp. B = {b}), then A ◊ B is denoted by a ◊ B (resp. A ◊ b). Note that the sets A ◊ B and B ◊ A are not necessarily equal. If G is Abelian, then A ◊ B = B ◊ A.
Definition 2.4.
|
Let (G, ◊) be a group, H a subgroup of G and 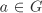 . The set a ◊ H is called the left coset of a with respect to H and the set H ◊ a is called the right coset of a with respect to H. If G is Abelian, then a left coset is naturally a right coset and vice versa. In that case, we call a ◊ H (or H ◊ a) simply a coset. . The set a ◊ H is called the left coset of a with respect to H and the set H ◊ a is called the right coset of a with respect to H. If G is Abelian, then a left coset is naturally a right coset and vice versa. In that case, we call a ◊ H (or H ◊ a) simply a coset.
|
From now onward, we consider left cosets only and call them cosets. If the underlying group is Abelian, then they are the same thing. The theory of right cosets can be parallelly developed, but we choose to omit that here. For simplicity, we also assume that the group G is a multiplicative group, so that the operation ◊ would be replaced by · (or by mere juxtaposition).
Proposition 2.2.
|
Let G be a (multiplicative) group and H a subgroup of G. Then, the cosets aH, 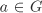 , partition G. Two cosets aH and bH are equal if and only if , partition G. Two cosets aH and bH are equal if and only if  . There is a bijective map from aH to bH for every a, . There is a bijective map from aH to bH for every a,  . .
Proof
We define a relation ~ on G such that a ~ b if and only if 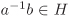 . Clearly, a ~ a. Now a ~ b implies . Clearly, a ~ a. Now a ~ b implies  , so that , so that  (See Exercise 2.8), that is, b ~ a. Finally, a ~ b and b ~ c imply a ~ c, since a–1c = (a–1b)(b–1c). Thus ~ is an equivalence relation on G and hence by Theorem 2.1 produces a partition of G. We now show that the equivalence class [a] of (See Exercise 2.8), that is, b ~ a. Finally, a ~ b and b ~ c imply a ~ c, since a–1c = (a–1b)(b–1c). Thus ~ is an equivalence relation on G and hence by Theorem 2.1 produces a partition of G. We now show that the equivalence class [a] of 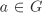 is the coset aH. This follows from that is the coset aH. This follows from that 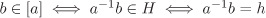 for some for some  for some for some  . .
Now we define a map 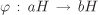 by ah ↦ bh for every by ah ↦ bh for every 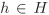 . The map is clearly surjective. Injectivity of . The map is clearly surjective. Injectivity of 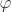 follows from the left cancellation law (Proposition 2.1). Hence follows from the left cancellation law (Proposition 2.1). Hence  is bijective. is bijective.
|
The following theorem is an important corollary to the last proposition.
Theorem 2.2. Lagrange’s theorem
|
Let G be a finite group and H a subgroup of G. Then, the cardinality of G is an integral multiple of the cardinality of H.
Proof
From Proposition 2.2, the cosets form a partition of G and there is a bijective map from one coset to another. Hence by Exercise 2.3 all cosets have the same cardinality. Finally, note that H is the coset of the identity element.
|
Definition 2.5.
|
Let G be a group and H a subgroup of G. The number of distinct cosets of H in G is called the index of H in G and is denoted by [G : H]. If G is finite, then [G : H] = #G/#H.
|
Definition 2.6.
|
Let H be a subgroup of a (multiplicative) group G. Then H is called a normal subgroup of G, if (aH)(bH) = (abH) for all a,  . It is clear that any subgroup H of an Abelian group G satisfies this condition and hence is normal. . It is clear that any subgroup H of an Abelian group G satisfies this condition and hence is normal.
If H is a normal subgroup of a group G, then the cosets aH, 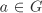 , form a group with multiplication defined by (aH)(bH) = (abH). This group is called the quotient group of G with respect to H and is denoted by G/H. , form a group with multiplication defined by (aH)(bH) = (abH). This group is called the quotient group of G with respect to H and is denoted by G/H.
|
Example 2.3.
For any group G with identity e, the trivial subgroups G and {e} are normal. G/G is a group with a single element, whereas G/{e} is essentially the same as the group G.
|
2.3.3. Homomorphisms
Definition 2.7.
|
Let (G, ◊) and (G′, ⊙) be groups. A function f : G → G′ is called a homomorphism (of groups), if f(a ◊ b) = f(a) ⊙ f(b) for all a,  , that is, if f commutes with the group operations of G and G′. , that is, if f commutes with the group operations of G and G′.
A group homomorphism f : G → G′ is called an isomorphism, if there exists a group homomorphism g : G′ → G such that g ο f = idG and f ο g = idG′. It can be easily seen that a homomorphism f : G → G′ is an isomorphism if and only if f is bijective as a function. If there exists an isomorphism f : G → G′, we say that the groups G and G′ are isomorphic and write G ≅ G′.
A homomorphism f from G to itself is called an endomorphism (of G). An endomorphism which is also an isomorphism is called an automorphism. The set of all automorphisms of a group G is a group under function composition. We denote this group by Aut G.
|
Example 2.4.
Proposition 2.3.
|
Let f be a group homomorphism from (G, ◊) to (G′, ⊙). Let e and e′ denote the identity elements of G and G′ respectively. Then f(e) = e′. If a, 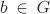 and c, and c, 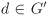 satisfy a ◊ b = e, c ⊙ d = e′ and f(a) = c, then f(b) = d. satisfy a ◊ b = e, c ⊙ d = e′ and f(a) = c, then f(b) = d.
Proof
We have e′ ⊙ f(e) = f(e) = f(e ◊ e) = f(e) ⊙ f(e), so that by right cancellation f(e) = e′. To prove the second assertion we note that c ⊙ d = e′ = f(e) = f(a ◊ b) = f(a) ⊙ f(b) = c ⊙ f(b). Thus f(b) = d.
|
Definition 2.8.
|
With the notations of the last proposition we define the kernel of f to be the following subset of G:
Ker  . .
We also define the image of f to be the subset
Im 
of G′. Then we have the following important theorem.
|
Theorem 2.3. Isomorphism theorem
|
Ker f is a normal subgroup of G, Im f is a subgroup of G′, and G/ Ker f ≅ Im f.
Proof
In order to simplify notations, let us assume that G and G′ are multiplicatively written groups. For u,  , we have f(uv–1) = f(u)(f(v))–1 = e′, that is, , we have f(uv–1) = f(u)(f(v))–1 = e′, that is,  . By Exercise 2.8, Ker f is a subgroup of H. We now show that it is normal. Note that for . By Exercise 2.8, Ker f is a subgroup of H. We now show that it is normal. Note that for  and and 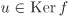 we have f(aua–1) = f(a)f(u)f(a–1) = e′, that is, we have f(aua–1) = f(a)f(u)f(a–1) = e′, that is, 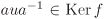 , since f(u) = e′ and f(a–1) = f(a)–1. By Exercise 2.10, Ker f is a normal subgroup of G. Now let a′ = f(a) and b′ = f(b) be arbitrary elements of Im f. Then, f(ab–1) = a′(b′)–1, that is, , since f(u) = e′ and f(a–1) = f(a)–1. By Exercise 2.10, Ker f is a normal subgroup of G. Now let a′ = f(a) and b′ = f(b) be arbitrary elements of Im f. Then, f(ab–1) = a′(b′)–1, that is,  . Thus, by Exercise 2.8 Im f is a subgroup of G′. . Thus, by Exercise 2.8 Im f is a subgroup of G′.
Now define a map 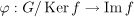 that takes a Ker f ↦ f(a). Let a Ker f = b Ker f. Then by Proposition 2.2, that takes a Ker f ↦ f(a). Let a Ker f = b Ker f. Then by Proposition 2.2, 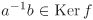 , that is, b = au for some , that is, b = au for some 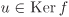 . But then f(b) = f(au) = f(a)f(u) = f(a)e′ = f(a). This shows that the map . But then f(b) = f(au) = f(a)f(u) = f(a)e′ = f(a). This shows that the map  is well-defined. It is easy to check that is well-defined. It is easy to check that 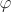 is a group homomorphism. Now is a group homomorphism. Now 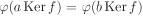 implies f(a) = f(b), that is, f(a–1b) = e′, that is, implies f(a) = f(b), that is, f(a–1b) = e′, that is,  , that is, a Ker f = b Ker f. Thus , that is, a Ker f = b Ker f. Thus  is injective. It is clearly surjective. Thus is injective. It is clearly surjective. Thus 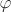 is bijective and hence an isomorphism from G/ Ker f to Im f. is bijective and hence an isomorphism from G/ Ker f to Im f.
|
2.3.4. Generators and Orders
Definition 2.9.
|
Let G be a group. In this section, we assume, unless otherwise stated, that G is multiplicatively written and has identity e. Let ai, 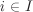 , be a family of elements of G. Consider the subset H of G defined as , be a family of elements of G. Consider the subset H of G defined as
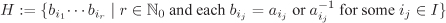
with the empty product (corresponding to r = 0) being treated as e. It is easy to check that H is a subgroup of G and contains all ai,  . We call H to be the subgroup generated by ai, . We call H to be the subgroup generated by ai, 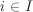 , or that the elements ai, , or that the elements ai, 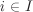 , generate H. H is called finitely generated, if it is generated by finitely many elements. In particular, H is called cyclic, if it is generated by a single element. If H is cyclic and generated by , generate H. H is called finitely generated, if it is generated by finitely many elements. In particular, H is called cyclic, if it is generated by a single element. If H is cyclic and generated by  , then g is called a generator or a primitive element of H. Note that, in general, a cyclic subgroup has more than one generators (Exercise 2.47). , then g is called a generator or a primitive element of H. Note that, in general, a cyclic subgroup has more than one generators (Exercise 2.47).
|
Example 2.5.
The group (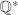 , ·) is generated by the “primes” p/1, , ·) is generated by the “primes” p/1, 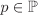 , and –1. , and –1. Let G be a multiplicative group (not necessarily Abelian) with identity e and let 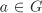 . Then the subgroup H generated by a is the set of elements of the form ar, . Then the subgroup H generated by a is the set of elements of the form ar, 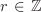 , and is always Abelian. If H is finite, then the elements ar, , and is always Abelian. If H is finite, then the elements ar, 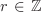 , cannot be all distinct, that is, as = at for some s, , cannot be all distinct, that is, as = at for some s, 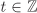 , s > t. Then as–t = e, where s – t > 0. Now a–1 = as–t–1 and, more generally, a–k = ak(s–t–1). Thus we may consider H to consist of non-negative powers of a only. Let , s > t. Then as–t = e, where s – t > 0. Now a–1 = as–t–1 and, more generally, a–k = ak(s–t–1). Thus we may consider H to consist of non-negative powers of a only. Let 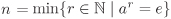 . It is easy to see that H = {ar | r = 0, . . . , n – 1}. . It is easy to see that H = {ar | r = 0, . . . , n – 1}.
|
Definition 2.10.
|
Let G be a finite group with identity e. The order of G is defined to be the cardinality of the set G and is denoted by ord G. The order of an element  is the cardinality of the subgroup of G generated by a and is denoted by ordG a or simply by ord a, when G is understood from the context. is the cardinality of the subgroup of G generated by a and is denoted by ordG a or simply by ord a, when G is understood from the context.
|
With these notations we prove the following important proposition.
Proposition 2.4.
|
The order m := ordG a of  is the smallest of the positive integers r for which ar = e. If n = ord G, then n is an integral multiple of m. In particular, an = e. is the smallest of the positive integers r for which ar = e. If n = ord G, then n is an integral multiple of m. In particular, an = e.
Proof
Let H be the (cyclic) subgroup of G generated by a. Then by Example 2.5 H = {ar | r = 0, . . . , m – 1} and m is the smallest of the positive integers r for which ar = e. By Lagrange’s theorem (Theorem 2.2), n is an integral multiple of m. That is, n = km for some 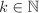 . But then an = (am)k = ek = e. . But then an = (am)k = ek = e.
|
Lemma 2.1.
|
Let G be a finite cyclic group. Then any subgroup of G is also cyclic.
Proof
Let G be generated by g and ord G = n. Then G = {gr | r = 0, . . . , n – 1}. The subgroup {e} of G is clearly cyclic. For an arbitrary subgroup H ≠ {e} of G, define 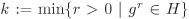 . Now take any . Now take any  and write r = qk + δ, where q and δ are respectively the quotient and remainder of division of r by k with 0 ≤ δ < k. Then gr = (gk)qgδ and so and write r = qk + δ, where q and δ are respectively the quotient and remainder of division of r by k with 0 ≤ δ < k. Then gr = (gk)qgδ and so  . The minimality of k implies that δ = 0, that is, gr = (gk)q. . The minimality of k implies that δ = 0, that is, gr = (gk)q.
|
Proposition 2.5.
|
Let G be a finite cyclic multiplicative group with identity e and let H be a subgroup of order m. Then an element  is an element of H if and only if am = e. is an element of H if and only if am = e.
Proof
If  , then am = e by Proposition 2.4. Conversely, assume that am = e, but a ∉ H. Let K be the subgroup of G generated by the elements of H and by a. By Lemma 2.1, K is cyclic. By assumption, K contains more than m elements (since H ∪ {a} ⊆ K). But every element of K has order dividing m, a contradiction. , then am = e by Proposition 2.4. Conversely, assume that am = e, but a ∉ H. Let K be the subgroup of G generated by the elements of H and by a. By Lemma 2.1, K is cyclic. By assumption, K contains more than m elements (since H ∪ {a} ⊆ K). But every element of K has order dividing m, a contradiction.
|
Finite cyclic groups play a crucial role in public-key cryptography. To see how, let G be a group which is finite, cyclic with generator g and multiplicatively written. Given  one can compute gr using ≤ 2 lg r + 2 group multiplications (See Algorithms 3.9 and 3.10). This means that if it is easy to multiply elements of G, then it is also easy to compute gr. On the other hand, there are certain groups for which it is very difficult to find out the integer r from the knowledge of g and gr, even when one is certain that such an integer exists. This is the basic source of security in many cryptographic protocols, like those based on finite fields, elliptic and hyperelliptic curves.
one can compute gr using ≤ 2 lg r + 2 group multiplications (See Algorithms 3.9 and 3.10). This means that if it is easy to multiply elements of G, then it is also easy to compute gr. On the other hand, there are certain groups for which it is very difficult to find out the integer r from the knowledge of g and gr, even when one is certain that such an integer exists. This is the basic source of security in many cryptographic protocols, like those based on finite fields, elliptic and hyperelliptic curves.
*2.3.5. Sylow’s Theorem
Sylow’s theorem is a powerful tool for studying the structure of finite groups. Recall that if G is a finite group of order n and if H is a subgroup of G of order m, then by Lagrange’s theorem m divides n. But given any divisor m′ of n, there need not exist a subgroup of G of order m′. However, for certain special values of m′, we can prove the existence of subgroups of order m′. Sylow’s theorem considers the case that m′ is a power of a prime.
Definition 2.11.
|
Let G be a finite group of cardinality n and let p be a prime. If n = pr for some  , we call G a p-group. More generally, let p be a prime divisor of n. Then a p-subgroup of G is a subgroup H of G such that H is a p-group. If H is a p-subgroup of G with cardinality pr for some , we call G a p-group. More generally, let p be a prime divisor of n. Then a p-subgroup of G is a subgroup H of G such that H is a p-group. If H is a p-subgroup of G with cardinality pr for some 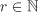 , then pr divides n. Moreover, if pr+1 does not divide n, then H is called a p-Sylow subgroup of G. , then pr divides n. Moreover, if pr+1 does not divide n, then H is called a p-Sylow subgroup of G.
|
We shortly prove that p-Sylow subgroups always exist. Before doing that, we prove a simpler result.
Theorem 2.4. Cauchy’s theorem
|
Let G be a finite group and p a prime dividing ord G. Then G has a subgroup of order p.
Proof
Let n := ord G. Note that if we can find an element 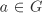 such that ord a = p, then the subgroup generated by a is the desired subgroup. To do that consider the set such that ord a = p, then the subgroup generated by a is the desired subgroup. To do that consider the set  consisting of all p-tuples (a1, . . . , ap) with consisting of all p-tuples (a1, . . . , ap) with  such that a1 . . . ap = e. such that a1 . . . ap = e.  consists of np–1 elements, since we can choose a1, . . . , ap–1 arbitrarily and independently from G and for each such choice of a1, . . . , ap–1 the value of ap = (a1 . . . ap–1)–1 gets fixed. Since p divides n, it follows that p divides consists of np–1 elements, since we can choose a1, . . . , ap–1 arbitrarily and independently from G and for each such choice of a1, . . . , ap–1 the value of ap = (a1 . . . ap–1)–1 gets fixed. Since p divides n, it follows that p divides  too. Now we define a relation ~ on too. Now we define a relation ~ on 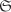 by (a1, . . . , ap) ~ (b1, . . . , bp) if and only if (b1, . . . , bp) = (ai, . . . , ap, a1, . . . , ai–1) for some by (a1, . . . , ap) ~ (b1, . . . , bp) if and only if (b1, . . . , bp) = (ai, . . . , ap, a1, . . . , ai–1) for some  (that is, (b1, . . . , bp) is a cyclic shift of (a1, . . . , ap)). It is easy to see that ~ is an equivalence relation on (that is, (b1, . . . , bp) is a cyclic shift of (a1, . . . , ap)). It is easy to see that ~ is an equivalence relation on 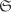 . The equivalence class of (a1, . . . , ap) contains 1 or p elements depending on whether a1 = · · · = ap or not. Let r and s be the the number of equivalence classes containing 1 and p elements of . The equivalence class of (a1, . . . , ap) contains 1 or p elements depending on whether a1 = · · · = ap or not. Let r and s be the the number of equivalence classes containing 1 and p elements of 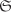 respectively. Then respectively. Then 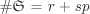 , so that p divides r. Since the equivalence class of (e, . . . , e) contains only one element, we must have r ≥ 1, that is, r ≥ p. This, in turn, proves the existence of , so that p divides r. Since the equivalence class of (e, . . . , e) contains only one element, we must have r ≥ 1, that is, r ≥ p. This, in turn, proves the existence of 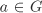 , a ≠ e, such that , a ≠ e, such that 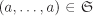 . But then ap = e. . But then ap = e.
|
Now we are in a position to prove the general theorem.
Theorem 2.5. Sylow’s theorem
|
Let G be a finite group of order n and let p be a prime dividing n. Then there exists a p-Sylow subgroup of G.
Proof
We proceed by induction on n. If n = p, then G itself is a p-Sylow subgroup of G. So we assume n > p and write n = prm, where p does not divide m. If r = 1, then the theorem follows from Cauchy’s theorem (Theorem 2.4). So we assume r > 1 and consider the class equation of G, namely,  (See Exercise 2.16). If p does not divide [G : C(a)] for some a ∉ Z(G), then #C(a) = #G/[G : C(a)] = prm′ < #G for some m′ < m. By induction, C(a) has a p-Sylow subgroup which is also a p-Sylow subgroup of G. On the other hand, if p divides [G : C(a)] for all a ∉ Z(G), then p divides #Z(G), as can be easily seen from the class equation. We apply Cauchy’s theorem on Z(G) to obtain a subgroup H of Z(G) with #H = p. By Exercise 2.16(b), H is a normal subgroup of G and we consider the canonical surjection μ : G → G/H. Since #(G/H) = pr–1m < n and r > 1, by induction G/H has a p-Sylow subgroup, say K. But then μ–1(K) is a p-Sylow subgroup of G. (See Exercise 2.16). If p does not divide [G : C(a)] for some a ∉ Z(G), then #C(a) = #G/[G : C(a)] = prm′ < #G for some m′ < m. By induction, C(a) has a p-Sylow subgroup which is also a p-Sylow subgroup of G. On the other hand, if p divides [G : C(a)] for all a ∉ Z(G), then p divides #Z(G), as can be easily seen from the class equation. We apply Cauchy’s theorem on Z(G) to obtain a subgroup H of Z(G) with #H = p. By Exercise 2.16(b), H is a normal subgroup of G and we consider the canonical surjection μ : G → G/H. Since #(G/H) = pr–1m < n and r > 1, by induction G/H has a p-Sylow subgroup, say K. But then μ–1(K) is a p-Sylow subgroup of G.
|
Note that if H is a p-Sylow subgroup of G and  , then gHg–1 is also a p-Sylow subgroup of G. The converse is also true, that is, if H and H′ are two p-Sylow subgroups of G, then there exists a
, then gHg–1 is also a p-Sylow subgroup of G. The converse is also true, that is, if H and H′ are two p-Sylow subgroups of G, then there exists a 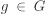 such that H′ = gHg–1. We do not prove this assertion here, but mention the following important consequence of it. If G is Abelian, then H′ = gHg–1 = gg–1H = H, that is, there is only one p-Sylow subgroup of G. If G is Abelian and
such that H′ = gHg–1. We do not prove this assertion here, but mention the following important consequence of it. If G is Abelian, then H′ = gHg–1 = gg–1H = H, that is, there is only one p-Sylow subgroup of G. If G is Abelian and 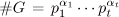 with pairwise distinct primes pi and with
with pairwise distinct primes pi and with  , then G is the internal direct product of its pi-Sylow subgroups, i = 1, . . . , t (Exercises 2.17 and 2.19).
, then G is the internal direct product of its pi-Sylow subgroups, i = 1, . . . , t (Exercises 2.17 and 2.19).
Exercise Set 2.3
| 2.8 | Let G be a multiplicatively written group (not necessarily Abelian). Prove the following assertions.
For all elements a,  , we have (ab)–1 = b–1a–1 and (a–1)–1 = a. , we have (ab)–1 = b–1a–1 and (a–1)–1 = a. A subset H of G is a subgroup of G if and only if 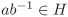 for all a, for all a, 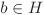 . .
|
| 2.9 | Let G be a multiplicatively written group and let H and K be subgroups of G. Show that:
H ∩ K is a subgroup of G. H ∪ K is a subgroup of G if and only if H ⊆ K or K ⊆ H. HK is a subgroup of G if and only if HK = KH. In particular, if K is normal in G, then HK is a subgroup of G. G × G is a group and H × K is a subgroup of G × G. If 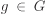 , then gHg–1 is a subgroup of G. , then gHg–1 is a subgroup of G.
|
| 2.10 |
Let G be a multiplicatively written group and H a subgroup of G. Show that the following conditions are equivalent: H is a normal subgroup of G. gHg–1 = H for all  . . gH = Hg for all 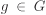 . .
Show that if [G : H] = 2, then H is normal.
|
| 2.11 | Let G be a (multiplicative) group.
Second isomorphism theorem Let H and K be subgroups of G and let K be normal in G. Show that H/(H ∩ K) ≅ (HK)/K. [H] Third isomorphism theorem Let H and K be normal subgroups of G with H ⊆ K. Show that G/K ≅ (G/H)/(K/H) (where 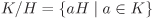 ). [H] ). [H]
|
| 2.12 |
Show that the only automorphisms of the group (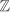 , +) are the identity map and the map that sends a ↦ –a. , +) are the identity map and the map that sends a ↦ –a. Show that the group of automorphisms of (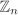 , +) is isomorphic to ( , +) is isomorphic to (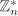 , ·). , ·).
|
| 2.13 | Let H be a subgroup of G generated by ai,  . Show that H is the smallest subgroup of G, that contains all of ai, . Show that H is the smallest subgroup of G, that contains all of ai,  . .
|
| 2.14 | Let  be a homomorphism of (multiplicative) groups. Show that: be a homomorphism of (multiplicative) groups. Show that:
If H is a subgroup of G, then 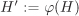 is a subgroup of G′. If is a subgroup of G′. If 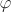 is surjective and H is normal, then H′ is also normal. is surjective and H is normal, then H′ is also normal. If H′ is a subgroup of G′, then  is a subgroup of G. If H′ is normal, then H is also normal. If is a subgroup of G. If H′ is normal, then H is also normal. If 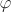 is surjective and H is normal, then H′ is also normal. is surjective and H is normal, then H′ is also normal. Correspondence theorem Let H be a normal subgroup of G. Then the subgroups (resp. normal subgroups) of G/H are in one-to-one correspondence with the subgroups (resp. normal subgroups) of G, that contain H. [H]
|
| 2.15 | Let G be a cyclic group. Show that G is isomorphic to 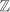 or to or to  for some for some 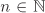 depending on whether G is infinite or finite. depending on whether G is infinite or finite.
|
| 2.16 | Let G be a finite (multiplicative) group (not necessarily Abelian).
We define the centre of G to be the set  . Show that Z(G) is a subgroup of G. . Show that Z(G) is a subgroup of G. If H ⊆ Z(G) is a subgroup of G, show that H is a normal subgroup of G. Define a relation ~ on G by a ~ b if and only if b = gag–1 for some  . Show that ~ is an equivalence relation on G. We say that the elements a and b of G are conjugate, if the equivalence classes [a] and [b] are the same. The equivalence classes are called the conjugacy classes of G. . Show that ~ is an equivalence relation on G. We say that the elements a and b of G are conjugate, if the equivalence classes [a] and [b] are the same. The equivalence classes are called the conjugacy classes of G. Show that the cardinality of the conjugacy class of 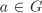 is equal to the index [G : C(a)]. is equal to the index [G : C(a)]. Deduce the class equation of G, that is, #G = #Z(G) + ∑[G : C(a)], where the sum is over a set of all pairwise non-conjugate a ∉ Z(G).
|
| 2.17 | Let G be a (multiplicative) Abelian group with identity e and order  , where pi are distinct primes and , where pi are distinct primes and 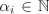 . For each i, let Hi be the pi-Sylow subgroup of G. Show that: . For each i, let Hi be the pi-Sylow subgroup of G. Show that:
Every element  can be written uniquely as g = h1 · · · hr with can be written uniquely as g = h1 · · · hr with  . Moreover, in that case we have ordG g = (ordH1 h1) · · · (ordHr hr). . Moreover, in that case we have ordG g = (ordH1 h1) · · · (ordHr hr). G is cyclic if and only if all of H1, . . . , Hr are cyclic.
|
| 2.18 | Let G be a finite (multiplicative) Abelian group with identity e. Assume that for every  there are at most n elements x of G satisfying xn = e. Show that G is cyclic. [H] there are at most n elements x of G satisfying xn = e. Show that G is cyclic. [H]
|
| 2.19 | Let G be a (multiplicative) group and let H1, . . . , Hr be normal subgroups of G. If G = H1 · · · Hr and every element  can be written uniquely as g = h1 · · · hr with can be written uniquely as g = h1 · · · hr with  , then G is called the internal direct product of H1, . . . , Hr. (For example, if G is finite and Abelian, then by Exercise 2.17 it is the internal direct product of its Sylow subgroups.) Show that: , then G is called the internal direct product of H1, . . . , Hr. (For example, if G is finite and Abelian, then by Exercise 2.17 it is the internal direct product of its Sylow subgroups.) Show that:
If G is finite, it is the internal direct product of normal subgroups H1, . . . , Hr if and only if G = H1 · · · Hr and Hi ∩ Hj = {e} for all i, j, i ≠ j. If G is the internal direct product of the normal subgroups H1, . . . , Hr, then G is isomorphic to the (external) direct product H1 × · · · × Hr. [H]
|
| 2.20 | Let Hi, i = 1, . . . , r, be finite Abelian groups of orders mi and let H := H1 × · · ·× Hr be their direct product. Show that H is cyclic if and only if each Hi is cyclic and m1, . . . , mr are pairwise coprime.
|
![]() (or
(or ![]() or
or ![]() ). Subtraction is not a binary operation on
). Subtraction is not a binary operation on ![]() , since, for example, 2 – 3 is not an element of
, since, for example, 2 – 3 is not an element of ![]() . Division is not a binary operation on
. Division is not a binary operation on ![]() , since division by zero is not defined. Division is a binary operation on
, since division by zero is not defined. Division is a binary operation on ![]() .
.![]() , then a1 ◊ ··· ◊ an represents a unique element of the group irrespective of how we insert brackets to compute the element a1 ◊ ··· ◊ an.
, then a1 ◊ ··· ◊ an represents a unique element of the group irrespective of how we insert brackets to compute the element a1 ◊ ··· ◊ an.![]() . In particular, if A = {a} (resp. B = {b}), then A ◊ B is denoted by a ◊ B (resp. A ◊ b). Note that the sets A ◊ B and B ◊ A are not necessarily equal. If G is Abelian, then A ◊ B = B ◊ A.
. In particular, if A = {a} (resp. B = {b}), then A ◊ B is denoted by a ◊ B (resp. A ◊ b). Note that the sets A ◊ B and B ◊ A are not necessarily equal. If G is Abelian, then A ◊ B = B ◊ A.![]() one can compute gr using ≤ 2 lg r + 2 group multiplications (See Algorithms 3.9 and 3.10). This means that if it is easy to multiply elements of G, then it is also easy to compute gr. On the other hand, there are certain groups for which it is very difficult to find out the integer r from the knowledge of g and gr, even when one is certain that such an integer exists. This is the basic source of security in many cryptographic protocols, like those based on finite fields, elliptic and hyperelliptic curves.
one can compute gr using ≤ 2 lg r + 2 group multiplications (See Algorithms 3.9 and 3.10). This means that if it is easy to multiply elements of G, then it is also easy to compute gr. On the other hand, there are certain groups for which it is very difficult to find out the integer r from the knowledge of g and gr, even when one is certain that such an integer exists. This is the basic source of security in many cryptographic protocols, like those based on finite fields, elliptic and hyperelliptic curves.![]() , then gHg–1 is also a p-Sylow subgroup of G. The converse is also true, that is, if H and H′ are two p-Sylow subgroups of G, then there exists a
, then gHg–1 is also a p-Sylow subgroup of G. The converse is also true, that is, if H and H′ are two p-Sylow subgroups of G, then there exists a ![]() such that H′ = gHg–1. We do not prove this assertion here, but mention the following important consequence of it. If G is Abelian, then H′ = gHg–1 = gg–1H = H, that is, there is only one p-Sylow subgroup of G. If G is Abelian and
such that H′ = gHg–1. We do not prove this assertion here, but mention the following important consequence of it. If G is Abelian, then H′ = gHg–1 = gg–1H = H, that is, there is only one p-Sylow subgroup of G. If G is Abelian and ![]() with pairwise distinct primes pi and with
with pairwise distinct primes pi and with ![]() , then G is the internal direct product of its pi-Sylow subgroups, i = 1, . . . , t (Exercises 2.17 and 2.19).
, then G is the internal direct product of its pi-Sylow subgroups, i = 1, . . . , t (Exercises 2.17 and 2.19).