7.2. Side-Channel Attacks
Side-channel attacks refer to a class of cryptanalytic tools for determining a private key by measuring signals (like timing, power fluctuation, electromagnetic radiation) from or by inducing faults in the device performing operations involving the private key. In this section, we describe three methods of side-channel cryptanalysis: timing attack, power attack and fault attack.
7.2.1. Timing Attack
Paul C. Kocher introduced the concept of side-channel cryptanalysis in his seminal paper [155] on timing attacks. Though not unreasonable, timing attacks are somewhat difficult to mount in practice.
Details of the attack
The private-key operation in many cryptographic systems (like RSA or discrete-log-based systems) is usually a modular exponentiation of the form
y := xd (mod n),
where d is the private key. The private-key procedure may involve other overheads (like message decoding), but the running time of the routine is usually dominated by and so can be approximated by the time of the modular exponentiation.
Assume that this exponentiation is carried out by a square-and-multiply algorithm known to Carol, the attacker. For example, suppose that Algorithm 3.9 is used. Each iteration of the for loop involves a modular squaring followed conditionally by a modular multiplication. The multiplication is done in an iteration if and only if the corresponding bit ei in the exponent is 1. Thus, an iteration runs slower if ei = 1 than if ei = 0. If Carol could measure the timing of each individual iteration of the for loop, she would correctly guess most (if not all) of the bits in the exponent. But it is unreasonable to assume that an attacker can collect such detailed timing data. Moreover, if Algorithm 3.10 is used, these detailed data do not help much, because in this case the timing of an individual iteration of the for loop can at best differentiate between the two cases ei = 0 and ei ≠ 0. There are 2t – 1 non-zero values for each ei.
However, it is not difficult to think of a situation where the attacker can measure, to a reasonable accuracy, the total time of the exponentiation. In order to guess d, Carol requires the times of the modular exponentiations for several different values of x, say x1, . . . , xk, all known to her. (Note that xi may be messages to be signed or intercepted ciphertexts.) The same exponent d is used for all these exponentiations. Let Ti be the time for computing ![]() (mod n), as measured by Carol. We may assume that all these k exponentiations are carried out on the same machine using the same routine.
(mod n), as measured by Carol. We may assume that all these k exponentiations are carried out on the same machine using the same routine.
Kocher considers the attack on the exponentiation routine of RSAREF, a cryptography toolkit available from the RSA Laboratories. This routine implements Algorithm 3.10 with t = 2. For the sake of convenience, the algorithm is reproduced below. We may assume that the exponent has an even number of bits—if not, pad a leading zero.
Algorithm 7.1. RSAREF’s exponentiation routine
Every step of the above algorithm runs in a time dependent on the operands. For example, the modular multiplication in Step (9) takes time dependent on the operands y and z(d2j+1d2j)2. The variation in the timing depends on the implementation of the modular arithmetic routines and also on the machine’s architecture. However, we make the assumption that for fixed operands each step requires a constant time on a given machine (or on identical machines). This is actually a loss of generality, since the running time of a complex step (like modular multiplication or squaring) for fixed operands may vary for various reasons like process scheduling, availability of cache, page faults and so on. It may be difficult, perhaps impossible, for an attacker to arrange for herself a verbatim emulation of the victim’s machine at the time when the latter performed the private-key operations. Let us still proceed with our assumption, say by conceiving of a not-so-unreasonable situation where the effects of these other factors are not sizable enough.
We use the subscript i to denote the i-th private-key operation for 1 ≤ i ≤ k. The entire routine takes time Ti for the i-th exponentiation, that is, for the input xi. This measurement may involve some (unknown) error which we denote by ei. The first four steps are executed only once during each call and take a total time of pi (precomputation time). The for loop is executed l times. We ignore the time needed to maintain the loop (like decrementing j) and also the time taken by the if statement in Step (8). Let si,j and ti,j be the times taken respectively by Steps (6) and (7), when the loop variable (j) assumes the value j. If Step (9) is executed, we denote by mi,j the time taken by this step, else we set mi,j := 0. It follows that
Equation 7.1

where the index in the sum decreases from l – 1 to 0 in steps of 1. Carol does not know this break-up (that is, the explicit values of ei, si,j, ti,j and mi,j), but she can make an inductive guess in the following way.
Carol manages a machine and a copy of the exponentiation software both identical to those of the victim. She then successively guesses the secret bit pairs d2l–1d2l–2, d2l–3d2l–4, d2l–5d2l–6 and so on. Assume that at some stage Carol has correctly determined the exponent bits d2j+1d2j for j = l–1, l–2, . . . , j′+1. Initially j′ = l–1. Using this information Carol computes d2j′ +1d2j′ as follows. Carol’s knowledge at this stage allows her to measure pi and si,j, ti,j, mi,j for j = l – 1, . . . , j′ + 1 — she simply runs Algorithm 7.1 on xi. Carol then enters the loop with j = j′. The squaring operations are unconditional. Carol has the exact operands as the victim for the squaring steps. So Carol also measures si,j′ and ti,j′.
The bit pair d2j′+1d2j′ (considered as a binary integer) can take any one of the four values g = 0, 1, 2, 3. Carol measures the time ![]() of Step (9) for each of the four choices of g and adds this time to the time taken by the algorithm so far, in order to obtain:
of Step (9) for each of the four choices of g and adds this time to the time taken by the algorithm so far, in order to obtain:
Equation 7.2
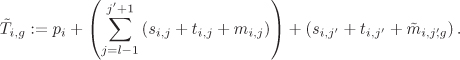
Kocher observed that the distribution of Ti, i = 1, . . . , k, is statistically related to that of ![]() only for the correct guess g. In order to see how, we subtract Equation (7.2) from Equation (7.1) to get:
only for the correct guess g. In order to see how, we subtract Equation (7.2) from Equation (7.1) to get:
Equation 7.3
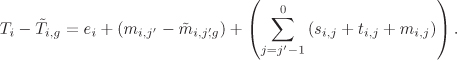
Let us assume that the error term ei is distributed like a random variable E. Similarly suppose that each multiplication (resp. squaring) has the distribution of a random variable M (resp. S). Taking the variance of Equation (7.3) over the values i = 1, 2, . . . , k and assuming that the sample size k is so large that the sample variances are very close to the variances of the respective random variables, we obtain:
Equation 7.4
![]()
where λ denotes the number of times Step (9) is executed for j = j′ – 1, . . . , 0. Note that λ is dependent on the private key and not on the arguments to the exponentiation routine. For the correct guess g, we have ![]() and so
and so
![]()
On the other hand, for an incorrect guess g we have:
![]()
if one of mi,j′ or ![]() is zero, or
is zero, or
![]()
if both mi,j′ and ![]() are non-zero. (Recall that Var(αX + βY) = α2 Var(X) + β2 Var(Y) for any real α, β.)
are non-zero. (Recall that Var(αX + βY) = α2 Var(X) + β2 Var(Y) for any real α, β.)
Calculation of the sample variances of ![]() for the four choices of g gives Carol a handle to determine (or guess) the correct choice. Carol simply takes the g for which the variance is minimum. This is the fundamental observation that makes the timing attack work.
for the four choices of g gives Carol a handle to determine (or guess) the correct choice. Carol simply takes the g for which the variance is minimum. This is the fundamental observation that makes the timing attack work.
Of course, statistical irregularities exist in practice, and the approximation of the actual variances by the sample variances introduces errors in Equation (7.4). These errors are of particular concern for large values of j′, that is, during the beginning of the attack. However, if an incorrect guess is made at a certain stage, this is detected soon with high probability, as Carol proceeds further. Suppose that an erroneous guess of d2j″ + 1d2j″ has been made for some j″ > j′. This means that the values of y are different from the actual values starting from the iteration of the loop with j = j″ – 1. (We may assume that most, if not all, xi ≠ 1.) We then do not have a cancellation of the timings for j = j″ – 1, . . . , j′. More correctly, if the guesses for j = l – 1, . . . , j″ + 1 are correct and the first error occurs at j = j″, then denoting the subsequent timings by ![]() one gets
one gets
Equation 7.5

Since each of the square and multiplication operations takes y as an operand, the original timings and the measured timings (the ones with hat) behave like independent variables and, therefore, taking the variance of Equation (7.5) yields
![]()
for some λ′ depending on the private key and on the previous guesses, but independent of the current guess g. In other words, Carol loses a meaningful relation of Var ![]() with the correctness of the current guess. Once Carol notices this, she backtracks and changes older guesses until the expected behaviour is restored. Thus, the timing attack comes with an error detection and correction strategy.
with the correctness of the current guess. Once Carol notices this, she backtracks and changes older guesses until the expected behaviour is restored. Thus, the timing attack comes with an error detection and correction strategy.
An analysis done by Kocher (neglecting E and assuming normal distributions for S and M) shows that Carol needs k = O(l) for a good probability of success.
Countermeasures
There are several ways in which timing attacks can be prevented.
If every multiplication step takes exactly the same time and so does every squaring step, the above timing attack does not work. Thus, forcing each multiplication and each squaring take the same respective times independent of their operands disallows Carol to mount the timing attack. Making mi,j constant alone does not suffice, for difference in square timings can be exploited in subsequent iterations to correct a guess. Forcing every operation take exactly the same time as the slowest possibility makes the implementation run slower. Moreover, finding the slowest possibility may be difficult.
Interleaving random delays also makes timing attacks difficult to mount, because the attacker then requires more number of samples in order to smooth out the effect of the delays. But again adding delays harms performance and does not completely rule out the possibility of timing attacks.
Perhaps the best strategy to thwart timing attacks is to use a random pair (u, v) with v := u–d (mod n) for each private-key operation. Initially x is multiplied by u and then the product ux is exponentiated to get udxd ≡ v–1y (mod n). Multiplication by v then yields the desired y. A new random pair (u, v) must be used for every exponentiation. However, the exponentiation v := u–d (mod n) is too costly to be performed during every private-key operation and may itself invite timing attacks. A good trade-off is to choose (u, v) once, keep it secret and for the next private-key operation update (and replace) the old (u, v) by (u′, v′) with u′ ≡ ue (mod n) and v′ ≡ ve (mod n) for some small e (random or deterministic). The choice e = 2 is quite satisfactory in practice—performing two modular squares is much cheaper than computing the full exponentiation v := u–d (mod n).
7.2.2. Power Analysis
In connection with timing attacks, we mentioned that if an adversary were able to measure the timing of each iteration of the square-and-multiply loop during an RSA (or discrete-log-based) private-key exponentiation, she could guess the bits in the key quite efficiently from only a few timing measurements. But it is questionable if such detailed timing data can be made available.
Now, think of a situation where Carol can measure patterns of power consumption made by the decrypting (or signing) device during one or more private-key operations with Alice’s private key. If Alice carries out the private-key operations in her personal workstation, it is difficult for Carol to conduct such measurements. So assume that Alice is using a smart card with a device to which Carol has a control. Carol inserts a small resistor in series with the line which drives Alice’s smart card. The power consumed by the smart-card circuit is roughly proportional to the current through the resistor. Measuring the voltage across the resistor (and multiplying by a suitable factor) Carol can observe the power consumed by Alice’s decryption device. Carol has to use a power measuring device that takes readings at a high frequency (100 MHz to several GHz depending on the budget of Carol). A set of power measurements obtained during a cryptographic operation is called a power trace. We now study how power traces can reveal Alice’s secrets.
Simple power analysis (SPA)
The individual steps in a private-key operation may be nakedly exposed in a power trace. This is, in particular, the case when different steps consume different amounts of power and/or take different times. Obtaining information about the operation of the decrypting device and/or the secrets by a direct interpretation of power traces is referred to as simple power analysis or SPA in short.
As an example of SPA, consider an implementation of RSA exponentiation using the naive square-and-multiply Algorithm 3.9. Here, the most power-consuming operations are modular squaring and modular multiplication. Modular multiplication typically runs slower than modular squaring. Also modular multiplication requires two different operands to fetch from the memory, whereas modular squaring requires only one operand. Thus, a multiplication operation has more and longer power requirements than a squaring operation.
A hypothetical[1] SPA trace during a portion of an RSA private-key operation is shown in Figure 7.1. Each spike in the trace corresponds to either a square or a multiplication operation. Let us assume that the power consumption is measured with sufficient resolution, so that no spike is missed. Since multiplication runs longer (and requires more operands) than squaring, multiplication spikes are wider than squaring spikes.
[1] SPA traces from real-life experiments on smart cards, as reported in several references, look similar to this. We, however, generated the trace using a random number generator. Absolute conformity to reality is not always crucial for the purposes of illustration.
Figure 7.1. Simulated SPA trace for a portion of an RSA private-key operation
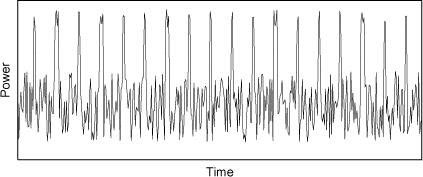
Let us denote a squaring operation by S and a multiplication operation by M. We observe that Alice’s smart card performs the sequence
SMSMSSMSSSSMSSSMSS
of operations during the measurement interval shown. Since multiplication in an iteration of the loop is skipped if and only if the corresponding bit in the exponent is zero, we can group the operations as
(SM)(SM)(S)(SM)(S)(S)(S)(SM)(S)(S)(SM)(S)(S.
This, in turn, reveals the bit string 110100010010 in Alice’s private key.
Effective as it appears, SPA, in practice, does not pose a huge threat to the security of conventional cryptographic systems. Using algorithms for which power traces do not bear direct relationships with the bits of the private key largely reduces risks of fruitful SPA. The inefficient repeated square-and-multiply Algorithm 7.2 always performs a multiplication after squaring and thereby eliminates chances of a successful SPA.
Algorithm 7.2. SPA-resistant exponentiation
|
Input: Output: y := xd (mod n). Steps: y := 1. |
Using the (more efficient) Algorithm 7.1 also frustrates SPA. Some chunks of two successive 0 bits are anyway revealed by power traces collected during the execution of this algorithm. But, for a decently large and random private key, this still leaves Carol with many unknown bits to be guessed. Note, however, that neither of the three remedies suggested to thwart the timing attack on Algorithm 7.1 seems to be effective in the context of SPA. Delays normally do not consume much power (unless some power-intensive dummy computations fill up the delays). Also, the masking of (x, y) by (u, v) fails to produce any alteration in the power consumption pattern during exponentiation.
If some private-key algorithm has unavoidable branchings due to individual bits in the private key, SPA can prove to be a notorious botheration.
Differential power analysis (DPA)
A carefully designed algorithm (like Algorithm 7.2) does not reveal key information from a simple observation of power traces. Moreover, the observed power traces may be corrupted by noise to an extent where SPA is not feasible. In such cases, differential power analysis (DPA) often helps the cryptanalyst reduce the effects of noise and exploit subtle correlation of power consumption patterns with specific bits in the operands. DPA requires availability of power traces from several private-key operations with the same key.
Consider the SPA-resistant Algorithm 7.2. Suppose that k power traces P1(t), . . . , Pk(t) for the computations of ![]() (mod n), i = 1, . . . , k, are available to Carol, that the ciphertexts x1, . . . , xk are known to Carol and that d = (dl–1 · · · d1d0)2. Carol successively guesses the bits dl–1, dl–2, dl–3, . . . of the exponent. Suppose that Carol has correctly guessed dj for j = l – 1, . . . , j′ + 1. She now uses DPA to guess dj′.
(mod n), i = 1, . . . , k, are available to Carol, that the ciphertexts x1, . . . , xk are known to Carol and that d = (dl–1 · · · d1d0)2. Carol successively guesses the bits dl–1, dl–2, dl–3, . . . of the exponent. Suppose that Carol has correctly guessed dj for j = l – 1, . . . , j′ + 1. She now uses DPA to guess dj′.
Let e := (dl–1dl–2 · · · dj′ + 1)2. At the beginning of the for loop with j = j′ the variable y holds the value xe modulo n. The loop computes x2e and x2e+1 and assigns y the appropriate value. If dj′ = 0, then in the next iteration the loop computes x4e and x4e+1, whereas if dj′ = 1, then in the next iteration the loop computes x4e+2 and x4e+3. It follows that the algorithm handles the value x4e if and only if dj′ = 0.
For each i = 1, . . . , k, Carol computes ![]() (mod n). Carol then chooses a particular bit position (say, the least significant bit) and considers the bit bi of zi at this position. We make the assumption that there is some subsequent step (or substep) in the implementation for which the average power consumption Π0 for b = 0 is different from the average power consumption Π1 for b = 1.[2]
(mod n). Carol then chooses a particular bit position (say, the least significant bit) and considers the bit bi of zi at this position. We make the assumption that there is some subsequent step (or substep) in the implementation for which the average power consumption Π0 for b = 0 is different from the average power consumption Π1 for b = 1.[2]
[2] The exact step which exhibits differential bias toward an individual bit value is dependent on the implementation. If the implementation does not provide such a step, the attack cannot be mounted in this way. Initially, the DPA was proposed for DES, a symmetric encryption algorithm, in which such a dependence is clearly available. With asymmetric-key encryption, such a strong dependence of the power, consumed by a step, on an individual bit value is not obvious. One may, however, use other dividing criteria, like low versus high Hamming weight (that is, number of one-bits) in the operand, which bear more direct relationships with power consumption.
Carol partitions {1, . . . , k} into two subsets:
| I0 | := | {i | bi = 0}, |
| I1 | := | {i | bi = 1}. |
Carol computes the average power traces ![]() and
and ![]() and subsequently the differential power trace
and subsequently the differential power trace
![]()
First, let dj′ = 0. In this case, the routine handles ![]() and so the power consumption at some time τ is correlated to the bit bi of
and so the power consumption at some time τ is correlated to the bit bi of ![]() . At any other instant, the power consumption is uncorrelated to this particular bit value. Therefore, if the sample size is sufficiently large and if the measurement noise has mean at zero, we have:
. At any other instant, the power consumption is uncorrelated to this particular bit value. Therefore, if the sample size is sufficiently large and if the measurement noise has mean at zero, we have:
![]()
On the other hand, if dj′ = 1, the value ![]() never appears in the execution of the algorithm and so at every time t the power consumption is uncorrelated to the particular bit of
never appears in the execution of the algorithm and so at every time t the power consumption is uncorrelated to the particular bit of ![]() and so we expect
and so we expect
| Δ(t) ≈ 0 | for all t. |
Figure 7.2 illustrates the two cases.[3] If the differential power trace has a distinct spike, the guess dj′ = 0 is correct. So by observing the existence or otherwise of a spike, Carol determines whether dj′ = 0 or dj′ = 1.
[3] Once again, these are hypothetical traces obtained by random number generators.
Figure 7.2. Simulated DPA trace for a portion of an RSA private-key operation
(a) for the correct guess
(b) for an incorrect guess

The number k of samples required for a good probability of success depends on the bias Π1–Π0 relative to the measurement noise. We assume that ![]() . If the noise has a variance of σ2, then by the central limit theorem the noise in each average power trace
. If the noise has a variance of σ2, then by the central limit theorem the noise in each average power trace ![]() or
or ![]() has at each t an approximate variance 2σ2/k, and so in the differential power trace Δ(t) the noise has an approximate variance 4σ2/k. In order that the bias Π1 –Π0 stands out against the noise, we require
has at each t an approximate variance 2σ2/k, and so in the differential power trace Δ(t) the noise has an approximate variance 4σ2/k. In order that the bias Π1 –Π0 stands out against the noise, we require ![]() , say,
, say, ![]() , that is, k ≥ 64σ2/(Π1 – Π0)2.
, that is, k ≥ 64σ2/(Π1 – Π0)2.
Countermeasures
Several countermeasures can be adopted to prevent DPA, both in the software level and in the hardware level.
Interleaving random delays between instructions destroys the alignment of the time τ in different power traces. Using a clock with randomly varying tick-rate has a similar effect. The delays should be such that they cannot be easily analyzed and subsequently removed. Random delays increase the number of samples required for a successful DPA to an infeasible value.
Suitable implementations of the power-critical steps destroy the power consumption signature of these steps. For example, one may go for an implementation that exhibits a constant power consumption pattern irrespective of the operands. Another possibility is replacement of complex critical instructions by atomic instructions (like assembly instructions) for which the dependence of power consumption on operands is less or difficult to analyze. However, the assumption that one can measure power at any resolution (perhaps at infinite resolution, say, using an analog device) indicates that this countermeasure challenges only the attacker’s budget.
Masking (x, y) by multiplying with (u, v) (as we did to prevent timing attacks) also eliminates chances of mounting successful DPA. One has to use a fresh mask for each private-key operation. Random unknown masks destroy the correlation of the bit values bi with power consumption. That is, the chosen bit bi of
 behaves randomly in relation to the same bit of (uixi)4e and so the differential power trace no longer leaks the bias Π1 – Π0.
behaves randomly in relation to the same bit of (uixi)4e and so the differential power trace no longer leaks the bias Π1 – Π0.Another strategy to foil DPA is to use randomization in the private exponent d. Instead of computing y := xd (mod n), one chooses a small random integer r (typically of bit size ≤ 20) and computes y := xd+rh (mod n), where h is φ(n) for RSA or the order of the discrete-log (sub)group. Since d = O(h) typically, the performance of the exponentiation routine does not deteriorate much. But random values of r during different private-key operations change the exponent bits in an unpredictable manner.
Quick changes in the exponent (the private key, that is, the key pair) also prevent the attacker to gather sufficiently many power traces for mounting a successful DPA. A key-use counter can be employed for this purpose. Whenever a given private key has been used on a small predetermined number of occasions, the key pair is updated.
Hardware shielding of the decrypting device also reduces DPA possibilities. For example, in-chip buffers between the external power source and the chip processor have been proposed to mask off the variation of internal power from external measurements. Such hardware countermeasures are, in general, somewhat costlier than software countermeasures.
Paul Kocher asserts: DPA highlights the need for people who design algorithms, protocols, software, and hardware to work closely together when producing security products.
7.2.3. Fault Analysis
We finally come to the third genre of side-channel cryptanalysis. We investigate how hardware faults occurring during private-key operations can reveal the secret to an adversary. There are situations where a single fault suffices. Boneh et al. [30] classify hardware faults into three broad categories.
Transient faults These are faults caused by random (unpredictable) hardware malfunctioning. These may be the outcomes of occasional flips of bit values in registers or of temporary erroneous outputs from logic or arithmetic circuits in the processor. These faults are called transient, because they are not repeated. It is rather difficult to detect such (silent) faults.
Latent faults These are faults generated by some permanent malfunctioning and/or bugs inherent in the processor. For example, the floating-point bug in the early releases of the Pentium processor may lead to latent faults. Latent faults are permanent, that is, repeated, but may be difficult to locate in practice.
Induced faults An induced fault is deliberately caused by an adversary. For example, a short surge of electromagnetic radiation may cause a smart card to malfunction temporarily. A malicious adversary can induce such temporary hardware faults to extract secret information from the smart card. It is, however, difficult to induce deliberate faults in a remote workstation.
Although induced faults appear to be the ones to guard against most seriously, the other two types of faults are also of relevance. Consider a certifying authority signing many messages. Transient and/or unknown latent faults may reveal the authority’s private key to a user who can later utilize this knowledge to produce false certificates.
Fault attack on RSA based on CRT
Consider the implementation of RSA private-key operation based on the CRT combination of the values obtained by exponentiation modulo the prime divisors p and q of the modulus n (Algorithm 5.4). Suppose that m is a message to be signed and s := md (mod n) the corresponding signature, where d is the signer’s private key. The CRT-based implementation computes s1 := s (mod p) and s2 := s (mod q). Assume that due to hardware fault(s) exactly one of s1 and s2 is wrongly computed. Say, s1 is incorrectly computed as ![]() . The corresponding faulty signature is denoted by
. The corresponding faulty signature is denoted by ![]() . We assume that the CRT combination of
. We assume that the CRT combination of ![]() and s2 is correctly computed.
and s2 is correctly computed.
An adversary requires the faulty signature ![]() and the correct signature s on the same message m in order to obtain the factor q of n. To see how, note that
and the correct signature s on the same message m in order to obtain the factor q of n. To see how, note that ![]() (mod p), s ≡ s1 (mod p) and
(mod p), s ≡ s1 (mod p) and ![]() (mod p), so that
(mod p), so that ![]() (mod p), that is,
(mod p), that is, ![]() . On the other hand,
. On the other hand, ![]() (mod q), that is,
(mod q), that is, ![]() . Therefore,
. Therefore,
![]()
This is how the fault analysis of Boneh et al. [30] works.
Arjen K. Lenstra et al. [142] point out that the knowledge of the faulty signature ![]() alone reveals the secret divisor q, that is, one does not require the genuine signature s on m. The verification key e of the signer is publicly known. Since RSA exponentiation is bijective,
alone reveals the secret divisor q, that is, one does not require the genuine signature s on m. The verification key e of the signer is publicly known. Since RSA exponentiation is bijective, ![]() (mod n). However,
(mod n). However, ![]() (mod q), and so
(mod q), and so ![]() (mod p). It follows that
(mod p). It follows that
![]()
Fault attack on RSA without CRT
Now, consider an implementation of RSA decryption based on a single exponentiation modulo n. For such an implementation, several models of fault attacks have been proposed. These attacks are less practical than the attack on CRT-based RSA just mentioned, because now one requires several faulty signatures in order to deduce the entire private key. Here, we present an attack due to Bao et al. [17].
As usual, the RSA modulus is n = pq and the signer’s key pair is (e, d). Consider a valid signature s on a message m. Let d = (dl–1 · · · d1d0)2 be the binary representation of the private key. Consider the powers:
| si ≡ m2i (mod n) | for i = 0, 1, . . . , l – 1. |
The signature s can be written as:
![]()
We assume that the attacker knows m and s and hence can compute si and ![]() modulo n for i = 0, . . . , l – 1. There is no harm in assuming that the message m is randomly chosen. (We may assume that randomly chosen integers are invertible modulo n, because encountering a non-invertible non-zero integer by chance is a stroke of unimaginable good luck and is tantamount to knowing the factors of n.)
modulo n for i = 0, . . . , l – 1. There is no harm in assuming that the message m is randomly chosen. (We may assume that randomly chosen integers are invertible modulo n, because encountering a non-invertible non-zero integer by chance is a stroke of unimaginable good luck and is tantamount to knowing the factors of n.)
In order to guess a bit of d, the attacker induces a fault in exactly one of the bits dj, changing it from dj to ![]() . The position j is random, that is, not under the control of the attacker. Now, the algorithm outputs the faulty signature
. The position j is random, that is, not under the control of the attacker. Now, the algorithm outputs the faulty signature
![]()
and so
![]()
A repetition in the values sl–1, . . . , s0, ![]() , . . . ,
, . . . , ![]() modulo n is again an incident of minuscule probability. Hence the attacker can uniquely identify the bit position j and the bit value dj in d by comparing
modulo n is again an incident of minuscule probability. Hence the attacker can uniquely identify the bit position j and the bit value dj in d by comparing ![]() with these 2l values.
with these 2l values.
Statistical analysis implies that the attacker needs to repeat this procedure about l log l times (on same or different (m, s) pairs) in order to ensure that the probability of identifying all the bits of d is at least 1/2.
Fault attack on the Rabin digital signature algorithm
Recall from Algorithm 5.34 that the Rabin signature algorithm uses CRT to combine s1 (mod p) and s2 (mod q). Thus, the attack on CRT-based RSA, described earlier, is applicable mutatis mutandis to the Rabin signature scheme. The computation of the square roots s1 and s2 demands the major portion of the running time of the routine. Inducing a fault during the execution is, therefore, expected to affect exactly one of s1 and s2, as desired by the attacker.
Fault attack on DSA
Bao et al. [17] propose a fault attack on the digital signature algorithm (DSA). We work with the notations of Algorithm 5.43 and Algorithm 5.44, except that, for maintaining uniformity in this section, we use m (instead of M) to denote the message to be signed. The (public) parameters are p, a prime divisor r of p – 1 of length 160 bits and an element ![]() of multiplicative order r. The signer’s DSA key pair is (d, gd(mod p)) with 1 < d < r.
of multiplicative order r. The signer’s DSA key pair is (d, gd(mod p)) with 1 < d < r.
Suppose that during the generation of a DSA signature, an attacker induces a fault in exactly one bit position of d changing it to ![]() . The routine generates the faulty signature
. The routine generates the faulty signature ![]() , where
, where

(d′, gd′) being the session key pair (not mutilated). As in the DSA signature-verification scheme, the attacker computes the following:

For each i = 0, . . . , l – 1 (where the bit length of d is l), the attacker also computes
![]()
Assume that the j-th bit dj of d is altered. If dj = 0, ![]() and so
and so
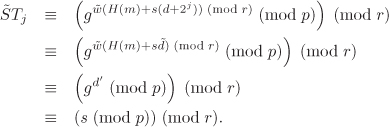
On the other hand, if dj = 1, then ![]() and a similar calculation shows that
and a similar calculation shows that
![]()
Thus, the attacker computes ![]() and
and ![]() for all j = 0, . . . , l – 1 and notices a unique match (with s). This discloses the position j and the corresponding bit dj.
for all j = 0, . . . , l – 1 and notices a unique match (with s). This discloses the position j and the corresponding bit dj.
Fault attack on the ElGamal signature scheme
A fault attack similar to that on the DSA scheme can be mounted on the ElGamal signature scheme. We here propose an alternative method proposed by Zheng and Matsumoto [315]. The novelty in their approach is that it performs the cryptanalysis of the ElGamal signature scheme by inducing fault on the pseudorandom bit generator of the signer’s smart card.
Algorithms 5.36 and 5.37 describe the ElGamal signature scheme on a general cyclic group G. Here, we restrict our attention to the specific group ![]() (though the following exposition works perfectly well for a general G). The parameters are a prime modulus p and a generator g of
(though the following exposition works perfectly well for a general G). The parameters are a prime modulus p and a generator g of ![]() . The signer’s key-pair is (d, gd(mod p)) for some d, 2 ≤ d ≤ p – 2.
. The signer’s key-pair is (d, gd(mod p)) for some d, 2 ≤ d ≤ p – 2.
In order to generate a signature (s, t) on a message m, a random session key d′ is generated and subsequently the following computations are carried out:
| s | ≡ | gd′ (mod p), |
| t | ≡ | d′–1(H(m) – dH(s)) (mod p – 1). |
Zheng and Matsumoto attack the generation of the session key d′. They propose the possibility that an abnormal physical stress (like low voltage) forces a constant output d0 for d′ from the pseudorandombit generator (software or hardware) in the smart card. First, assume that this particular value d0 is known a priori to the attacker. She then lets a message m generate a signature (s, t) with the session secret d0. The private key d is then immediately available from the equation:
d ≡ H(s)–1(H(m) – d0t) (mod p – 1).
Here, we assume that H(s) is invertible modulo p – 1.
If d0 is not known a priori, the attacker generates two signatures (s1, t1) and (s2, t2) on messages m1 and m2 respectively. Since d′ is always d0, we have s1 = s2 = s0, say. One can then easily calculate
d0 ≡ (t1 – t2)–1(H(m1) – H(m2)) (mod p – 1),
which, in turn, yields
d ≡ H(s0)–1(H(m1) – d0t1) (mod p – 1).
Fault attack on the Feige–Fiat–Shamir identification protocol
Let us conclude our repertoire of fault attack examples by explaining an attack on the FFS zero-knowledge identification protocol. This attack is again from Boneh et al. [30].
We use the notations of Algorithm 5.69. A modulus n = pq, p, ![]() , is first chosen (by Alice or by a trusted third party). Alice selects random x1, . . . ,
, is first chosen (by Alice or by a trusted third party). Alice selects random x1, . . . , ![]() and random bits δ1, . . . , δt, computes
and random bits δ1, . . . , δt, computes ![]() (mod n), publishes (y1, . . . , yt) and keeps (x1, . . . , xt) secret.
(mod n), publishes (y1, . . . , yt) and keeps (x1, . . . , xt) secret.
During an identification session with Bob, Alice generates a random commitment ![]() and sends to Bob the witness w := c2 (mod n). (For simplicity, we take γ of Algorithm 5.69 to be 0.) When Alice is waiting for a challenge from Bob, a fault occurs in her smart card changing the commitment c to c + E. Assume that the fault is at exactly one bit position, that is, E = ±2j for some
and sends to Bob the witness w := c2 (mod n). (For simplicity, we take γ of Algorithm 5.69 to be 0.) When Alice is waiting for a challenge from Bob, a fault occurs in her smart card changing the commitment c to c + E. Assume that the fault is at exactly one bit position, that is, E = ±2j for some ![]() , l being the bit length of c (or of n). This fault may be purposely induced by Bob with the malicious intention of guessing Alice’s secret (x1, . . . , xt).
, l being the bit length of c (or of n). This fault may be purposely induced by Bob with the malicious intention of guessing Alice’s secret (x1, . . . , xt).
Bob then generates a random challenge ![]() as usual. Upon reception of this challenge Alice computes and sends to Bob the faulty response
as usual. Upon reception of this challenge Alice computes and sends to Bob the faulty response
![]()
The knowledge of ![]() now aids Bob to obtain the product
now aids Bob to obtain the product ![]() as follows. First, note that
as follows. First, note that
![]()
so that
| for some |
There are only 4l possible values of (E, δ). Bob tries all these possibilities one by one. To simplify matters we assume that only one value of (E, δ) with E of the special form ±2j and with ![]() satisfies the last congruence. In practice, the existence of two (or more) solutions for (E, δ) is an extremely improbable phenomenon. For a guess of (E, δ), the commitment c can be computed as
satisfies the last congruence. In practice, the existence of two (or more) solutions for (E, δ) is an extremely improbable phenomenon. For a guess of (E, δ), the commitment c can be computed as
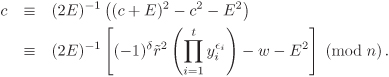
The correctness of the guess (E, δ) can be verified from the relation w ≡ c2 (mod n). Bob can now compute the desired product
![]()
In order to strengthen the confidence about the correctness of T, Bob may repeat the protocol once more with the same values of ∊1, . . . , ∊t, but under normal conditions (that is, without faults). This time he obtains w′ ≡ (c′)2 (mod n) and r′ ≡ c′T (mod n), which together give (r′)2 ≡ w′T2 (mod n), a relation that proves the correctness of T.
Bob repeats the above procedure t times in order to generate the system:
Equation 7.6
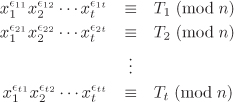
Here, ∊ki and Tk are known to Bob. Moreover, the exponents ∊ki can be so selected that the matrix (∊ki) is invertible modulo 2. In order to determine x1, Bob tries to find ![]() satisfying
satisfying
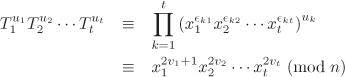
for some integers v1, . . . , vt. Comparing the coefficients gives the linear system

which can be solved for u1, . . . , ut, since the matrix (∊ki) is invertible modulo 2. The solution gives v1, . . . , vt and hence
![]()
Similarly, x2, . . . , xt can be determined up to sign. Plugging in these values of xi in System (7.6) and solving another linear system modulo 2 gives the exact signs of all xi.
Notice that Bob could have selected ∊ki = δki (where δ is the Dirac delta). For this choice, System (7.6) immediately gives x1, . . . , xt. But, in practice, Alice may disagree to respond to such simplistic challenges. Moreover, Bob must not raise any suspicion about a possible malpractice. For a general choice, all Bob has to do additionally is a little amount of simple linear algebra. The parameter t is rather small (typically less than 20); so this extra effort is of little concern to Bob.
Countermeasures
Fault analysis could be a serious threat, especially to smart-card users and certification authorities. We mention here some precautions to guard against such attacks. Some of these work for a general kind of fault attack, the others are specific to the algorithms they plan to protect.
One obvious general strategy is to perform the private-key operation twice and compare the results from the two executions. If the two results disagree, a fault must have taken place. It is then necessary to restart the computation from the beginning. This strategy slows down the implementation by a factor of two. Moreover, latent (permanent) faults cannot be detected by this method—the same error creeps in during every run.
It is sometimes easier to verify the correctness of the output by performing the reverse operation. For instance, after an RSA signature s ≡ md (mod n) is generated, one can check whether m ≡ se (mod n). If so, one can be reasonably confident about the correctness of s. If the RSA encryption exponent is small (like 3 or 257), this verification is quite efficient.
Ad hoc algorithm-specific tricks often offer effective and efficient checks for errors. Shamir [268] proposes the following check for CRT-based RSA signature generation. One chooses a small random prime r (say, of length ~ 32 bits) and computes s1 ≡ md (mod pr) and s2 ≡ md (mod qr). If s1 ≢ s2 (mod r), then one or both of the exponentiations went wrongly. If, on the other hand, s1 ≡ s2 (mod r), then s1 (mod p) and s2 (mod q) are combined by the CRT.
Maintaining extraneous error-checking data can guard against random bit flips. Parity check bits can detect the existence of single bit flips. Retaining a verbatim copy of a secret information d and comparison of the two copies at strategic instants can help detect more serious faults. It appears unlikely that both the copies can be affected by faults in exactly the same way. For discrete-log-based systems, maintaining d–1 in tandem with d appears to be a sound approach. Since the bits of d–1 are not in direct relationship with those of d, an attack on d cannot easily produce the relevant changes in d–1. As an example, consider the attack on DSA effected by toggling a bit of the secret key d. The second part of the signature can be generated in two ways: by computing t1 ≡ d′–1(H(m) + ds) (mod r) using d, and by computing t2 ≡ d′–1(d–1)–1(d–1H(m) + s) (mod r) using d–1. If t1 ≡ t2 (mod r), we can be pretty confident that this common value is the correct signature.
Appending random strings to the messages being signed also prevents timing attacks. Such random strings are not known to the adversary and cannot be easily recovered by the verification routine on a faulty signature. Also in this case the signer signs different strings on different occasions, even when the message remains the same.
Hardware countermeasures can also be adopted. Adequately shielded cards resist induced faults. In a situation described by Zheng and Matsumoto, the card should refuse to work instead of generating constant random bits. In the scenario of fault analysis, it, however, appears that robustness can be implanted easily at the software level. At any rate, sloppy hardware designs are never advocated.
Exercise Set 7.2
| 7.1 | Consider the notations of Section 7.2.1. Assume that mi,j is constant for all i, j (and irrespective of d2j+1d2j), but the square times si,j and ti,j vary according to their operands. Device a timing attack on such a system. |
| 7.2 | Show that under reasonable assumptions the SPA-resistant Algorithm 7.2 can be crypt-analyzed by timing attacks. |
| 7.3 | Recall that SPA of Algorithm 7.1 may leak partial information on the private key (some 00 sequences in the key). Rewrite the algorithm to prevent this leakage. |
| 7.4 | Assume that in Bao et al.’s attack on RSA described in the text, the attacker can induce faults in exactly two bit positions of d. Suggest how the two bits of d at these positions can be revealed from the resulting faulty signature. |
| 7.5 | Consider a variant of the Bao et al.’s attack on RSA described in the text, in which the valid signature s on m is unknown to the attacker. Explain how the position j of the erroneous bit and the bit dj at this position can still be identified. [H] |
| 7.6 | Bao et al. [17] propose an alternate fault analysis on RSA with square-and-multiply exponentiation. Use the notations (n, e, d, m, s, si) as in the text. Assume that the attacker knows an (m, s) pair and can induce a fault in exactly one of the values sj (and nowhere else) and generate the corresponding faulty signature. Suggest a strategy how the position j and the bit dj can be recovered in this case. |
| 7.7 | Propose a fault attack on the ElGamal signature scheme (Algorithms 5.36 and 5.37), similar to the attack on DSA described in the text. |
