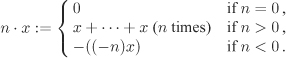2.7. Vector Spaces and Modules

Vector spaces and linear transformations between them are the central objects of study in linear algebra. In this section, we investigate the basic properties of vector spaces. We also generalize the concept of vector spaces to get another useful class of objects called modules. A module which also carries a (compatible) ring structure is referred to as an algebra. Study of algebras over fields (or more generally over rings) is of importance in commutative algebra, algebraic geometry and algebraic number theory.

2.7.1. Vector Spaces

Unless otherwise specified, K denotes a field in this section.

Definition 2.42.

A vector space V over a field K (or a K-vector space, in short) is an (additively written) Abelian group V together with a multiplication map · : K × V → V called the scalar multiplication map, such that the following properties are satisfied by every a, and x, .

  1. a · (x + y) = a · x + a · y,

  2. (a + b) · x = a · x + b · x,

  3. 1 · x = x,

  4. a · (b · x) = (ab) · x,

where ab denotes the product of a and b in the field K. When no confusions are likely, we omit the scalar multiplication sign · and write a · x simply as ax.

Example 2.12.

  1. Any field K is trivially a K-vector space with the scalar multiplication being the same as the field multiplication. More generally, if K ⊆ L is a field extension, then L is a K-vector space.

  2. For , the product Kn = K × · · · × K (n factors) is a K-vector space under the scalar multiplication map a(x1, . . . , xn) := (ax1, . . . , axn). For arbitrary K-vector spaces V1, . . . , Vn, we can analogously define the product V1 × · · · × Vn.

  3. The polynomial ring K[X] (or K[X1, . . . , Xn]) is a K-vector space (with the natural scalar multiplication).

Corollary 2.8.

Let V be a K-vector space. For every and , we have:

  1. 0 · x = 0.

  2. a · 0 = 0.

  3. (–a) · x = a · (–x) = –(a · x).

Proof

Easy verification.

Definition 2.43.

Let V be a vector space over K and S a subset of V. We say that S is a generating set or a set of generators of V (over K), or that S generates V (over K), if every element can be written as a finite linear combination x = a1x1 + · · · + anxn for some (depending on x) and with and for 1 ≤ i ≤ n. A generating set S of V is called minimal, if no proper subset of S generates V. If V has a finite generating set, then V is called finitely generated or finite-dimensional.

Example 2.13.

  1. Consider the field extension L := K[X]/〈f(X)〉 of K, where f is an irreducible polynomial in K[X] of degree n. If α denotes the equivalence class of X in L, then every element of L can be written as an–1αn–1 + · · · + a1α + a0 with for 0 ≤ i ≤ n – 1. Thus {1, α, . . . , αn–1} is a generating set of L over K. In particular, L is finitely generated over K.

  2. The K-vector space Kn is generated by the unit vectors ei, 1 ≤ i ≤ n, defined as ei := (0, . . . , 0, 1, 0, . . . , 0) (1 in the i-th position). Thus Kn is also finitely generated over K.

  3. {1, X, X2, · · ·} is an infinite generating set of the polynomial ring K[X] regarded as a K-vector space. K[X] is not finitely generated over K.

    It is not difficult to show that the generating sets discussed in these examples are minimal.

Definition 2.44.

A subset S of a K-vector space V is called linearly independent (over K), if whenever a1x1 + · · · + anxn = 0 for some , and , 1 ≤ i ≤ n, we have a1 = · · · = an = 0. If S is not linearly independent, it is called linearly dependent. If S is linearly independent (resp. dependent), then we also say that the elements of S are linearly independent (resp. dependent). A maximal linearly independent subset of V is a linearly independent subset S ⊆ V with the property that S ∪ {x} is linearly dependent for any .

If , then S is linearly dependent, since a · 0 = 0 for any . One can easily check that all the generating sets of Example 2.13 are linearly independent too. This is, however, not a mere coincidence, as the following result demonstrates.

Theorem 2.25.

A subset S of a K-vector space V is a minimal generating set for V if and only if S is a maximal linearly independent set of V.

Proof

[if] Given a maximal linearly independent subset S of V, we first show that S is a generating set for V. Take any non-zero . By the maximality of S, the set S ∪ {x} is linearly dependent, that is, there exists a linear relation of the form a0x + a1x1 + · · · + anxn = 0, , , with some ai ≠ 0. The linear independence of S forces a0 ≠ 0 and so is a finite linear combination of elements of S. Thus S generates V. Now, we show that S is minimal. Assume otherwise, that is, S′ := S {y} generates V for some . Since S is linearly independent, y ≠ 0. For some , , , we then have y = b1y1 + · · · + bmym, a contradiction to the linear independence of S.

[only if] Given a minimal generating set S of V, we first show that S is linearly independent. Assume not, that is, a1x1 + · · · + anxn = 0 for some , and with some ai, say a1, non-zero. But then and, therefore, S {x1} also generates V, a contradiction to the minimality of S. Thus S is linearly independent. Now choose a non-zero . Since S generates V, we can write y = b1y1 + · · · + bmym, , and , that is, 1y – b1y1 – · · · – bmym = 0, that is, S ∪ {y} is linearly dependent.

Definition 2.45.

Let V be a K-vector space. A minimal generating set S of V is called a basis of V over K (or a K-basis of V). By Theorem 2.25, S is a basis of V if and only if S is a maximal linearly independent subset of V. Equivalently, S is a basis of V if and only if S is a generating set of V and is linearly independent.

Any element of a vector space can be written uniquely as a finite linear combination of elements of a basis, since two different ways of writing the same element contradict the linear independence of the basis elements.

A K-vector space V may have many K-bases. For example, the elements 1, aX + b, (aX + b)2, · · · form a K-basis of K[X] for any a, , a ≠ 0. However, what is unique in any basis of a given K-vector space V is the cardinality[8] of the basis, as shown in Theorem 2.26.

[8] Two sets (finite or not) S1 and S2 are said to be of the same cardinality, if there exists a bijective map S1 → S2.

For the sake of simplicity, we sometimes assume that V is a finitely generated K-vector space. This assumption simplifies certain proofs greatly. But it is important to highlight here that, unless otherwise stated, all the results continue to remain valid without the assumption. For example, it is a fact that every vector space has a basis. For finitely generated vector spaces, this is a trivial statement to prove, whereas without our assumption we need to use arguments that are not so simple. (A possible proof follows from Exercise 2.63 with U = {0}.)

Theorem 2.26.

Let V be a K-vector space. Then any K-basis of V has the same cardinality.

Proof

We assume that V is finitely generated. Let S = {x1, . . . , xn} be a minimal finite generating set, that is, a basis, of V. Let T be another basis of V. Assume that m := #T > n. (We might even have m = ∞.) We can choose distinct elements . Note that xi and yj are non-zero. Now we can write y1 = a1x1 + · · · + anxn for some (unique) , with some ai ≠ 0. Renumbering x1, . . . , xn, if necessary, we may assume that a1 ≠ 0. Then . It follows that y1, x2, . . . , xn generate V. In particular, we can write y2 = b1y1 + b2x2 + · · · + bnxn, , with some bi ≠ 0. If b2 = · · · = bn = 0, then y1, y2 are linearly dependent, a contradiction. So bi ≠ 0 for some i, 2 ≤ i ≤ n. Again we may renumber x2, . . . , xn, if necessary, to assume that b2 ≠ 0. Then , that is, y1, y2, x3, . . . , xn generate V. Proceeding in this way we can show that y1, . . . , yn generate V, a contradiction to the minimality of T as a generating set. Thus we must have m ≤ n. In particular, m is finite. Now reversing the roles of S and T we can likewise prove that n ≤ m.

Theorem 2.26 holds even when V is not finitely generated. We omit the proof for this case here.

Definition 2.46.

Let V be a K-vector space. The cardinality of any K-basis of V is called the dimension of V over K and is denoted by dimK V (or by dim V, if K is understood from the context). We call V finite-dimensional (resp. infinite-dimensional), if dimK V is finite (resp. infinite).

For example, dimK Kn = n, , and dimK K[X] = ∞.

Definition 2.47.

Let V be a K-vector space. A subgroup U of V, which is closed under the scalar multiplication of V, is again a K-vector space and is called a (vector) subspace of V. In this case, we have dimK U ≤ dimK V (Exercise 2.63).

Example 2.14.

Let V be a vector space over K.

  1. The subset {0} and V are trivially subspaces of V.

  2. Let S be any subset of V (not necessarily linearly independent). Then the set is a vector subspace of V. We say that U is spanned or generated by S, or that S generates or spans U, or that U is the span of S. This is often denoted by or by U = Span S. If S is linearly independent, then S is a basis of U.

Definition 2.48.

Let V and W be K-vector spaces. A map f : V → W is called a homomorphism (of vector spaces) or a linear transformation or a linear map over K, if

f(ax + by) = af(x) + bf(y)

for all a, and x, . Equivalently, f is a linear map over K if and only if f(x + y) = f(x) + f(y) and f(ax) = af(x) for all and x, . The set of all K-linear maps V → W is denoted by HomK(V, W). HomK(V, W) is a K-vector space under the definitions (f + g)(x) := f(x) + g(x) and (af)(x) := af(x) for all f, and . A K-linear transformation V → V is called a K-endomorphism of V. The set of all K-endomorphisms of V is denoted by EndK V. A bijective[9] homomorphism (resp. endomorphism) is called an isomorphism (resp. automorphism).

[9] As in Footnote 2, we continue to be lucky here: The inverse of a bijective linear transformation is again a linear transformation.

Theorem 2.27.

Let V and W be K-vector spaces. Then V and W are isomorphic if and only if dimK V = dimK W.

Proof

If dimK V = dimK W and S and T are bases of V and W respectively, then there exists a bijection f : S → T. One can extend f to a linear map as , for , and . One can readily verify that is an isomorphism. Conversely, if g : V → W is an isomorphism and S is any basis of V, then is clearly a basis of W.

Corollary 2.9.

A K-vector space V with n := dimK V < ∞ is isomorphic to Kn.

Let V be a K-vector space and U a subspace. As in Section 2.3 we construct the quotient group V/U. This group can be given a K-vector space structure under the scalar multiplication map a(x + U) := ax + U, , . If T ⊆ V is such that the residue classes of the elements of T form a K-basis of V/U and if S is a K-basis of U, then it is easy to see that S ∪ T is a K-basis of V. In particular,

Equation 2.2


For , the set is called the kernel Ker f of f, and the set is called the image Im f of f. We have the isomorphism theorem for vector spaces:

Theorem 2.28. Isomorphism theorem

Ker f is a subspace of V, Im f is a subspace of W, and V/Ker f ≅ Im f.

Proof

Similar to Theorem 2.3 and Theorem 2.9.

Definition 2.49.

For , the dimension of Im f is called the rank of f and is denoted by Rank f, whereas the dimension of Ker f is called the nullity of f and is denoted by Null f. An immediate consequence of the isomorphism theorem and of Equation (2.2) is the following important result.

Theorem 2.29.

Rank f + Null f = dimK V for any .

*2.7.2. Modules

If we remove the restriction that K is a field and assume that K is any ring, then a vector space over K is called a K-module. More specifically, we have:

Definition 2.50.

Let R be a ring. A module over R (or an R-module) is an (additively written) Abelian group M together with a multiplication map · : R × M → M called the scalar multiplication map, such that for every a, and x, we have a · (x + y) = a · x + a · y, (a + b) · x = a · x + b · x, 1 · x = x, and a · (b · x) = (ab) · x, where ab denotes the product of a and b in the ring R. When no confusions are likely, we omit the scalar multiplication sign · and write a · x as ax.

Example 2.15.

  1. Vector spaces are special cases of modules, when the underlying ring is a field.

  2. Ideals of R are modules over R with the ring multiplication map taken as the scalar multiplication.

  3. Every Abelian group G is a -module under the scalar multiplication

  4. The polynomial rings R[X] and R[X1, . . . , Xn] are modules over R.

  5. Let Mi, , be a family of R-modules. The direct product of Mi is defined as the set of all tuples indexed by I. The direct sum is the subset of the Cartesian product consisting only of the tuples for which ai = 0 except for a finite number of . Both the direct product and the direct sum are R-modules under component-wise addition and scalar multiplication. When I is finite, they are naturally the same.

Modules are a powerful generalization of vector spaces. Any result we prove for modules is equally valid for vector spaces, ideals and Abelian groups. On the other hand, since we do not demand that the ring R be necessarily a field, certain results for vector spaces are not applicable for all modules.

It is easy to see that Corollary 2.8 continues to hold for modules. An R-submodule of an R-module M is a subgroup of M, that is closed under the scalar multiplication of M. For a subset S ⊆ M, the set of all finite linear combinations of the form a1x1 + · · · + anxn, , , , is an R-submodule N of M, denoted by RS or . We say that N is generated by S (or by the elements of S). If S is finite, then N is said to be finitely generated. A (sub)module generated by a single element is called cyclic. It is important to note that unlike vector spaces the cardinality of a minimal generating set of a module is not necessarily unique. (See Exercise 2.68 for an example.) It is also true that given a minimal generating set S of M, there may be more than one ways of writing an element of M as finite linear combinations of elements of S. For example, if and S = {2, 3}, then 1 = (–1)·2+1·3 = 2·2+(–1)·3. The nice theory of dimensions developed in connection with vector spaces does not apply to modules.

For an R-submodule N of M, the Abelian group M/N is given an R-module structure by the scalar multiplication map a(x + N) := ax + N. This module is called the quotient module of M by N.

For R-modules M and N, an R-linear map or an R-module homomorphism (from M to N) is defined as a map f : M → N with f(ax+by) = af(x)+bf (y) for all a, and x, (or equivalently with f(x + y) = f(x) + f(y) and f(ax) = af(x) for all and x, ). An isomorphism, an endomorphism and an automorphism are defined in analogous ways as in case of vector spaces. The set of all (R-module) homomorphisms M → N is denoted by HomR(M, N) and the set of all (R-module) endomorphisms of M is denoted by EndR M. These sets are again R-modules under the definitions: (f + g)(x) := f(x) + g(x) and (af)(x) := af(x) for all and (and f, g in HomR(M, N) or EndR M).

The kernel and image of an R-linear map f : M → N are defined as the sets Ker and Im . With these notations we have the isomorphism theorem for modules:

Theorem 2.30. Isomorphism theorem

Ker f and Im f are submodules of M and N respectively and M / Ker f ≅ Im f.

For an R-module M and an ideal of R, the set consisting of all finite linear combinations with , and is a submodule of M. On the other hand, for a submodule N of M the set is an ideal of R. In particular, the ideal (M : 0) is called the annihilator of M and is denoted as AnnR M (or as Ann M). For any ideal , one can view M as an under the map . One can easily check that this map is well-defined, that is, the product is independent of the choice of the representative a of the equivalence class .

Definition 2.51.

A free module M over a ring R is defined to be a direct sum of R-modules Mi with each Mi ≅ R as an R-module. If I is of finite cardinality n, then M is isomorphic to Rn.

Any vector space is a free module (Theorem 2.27 and Corollary 2.9). The Abelian groups , , are not free.

Theorem 2.31. Structure theorem for finitely generated modules

M is a finitely generated R-module if and only if M is a quotient of a free module Rn for some .

Proof

[if] The free module Rn has a canonical generating set ei, , where

ei = (0, . . . , 0, 1, 0, . . . , 0) (1 in the i-th position).

If M = Rn/N, then the equivalence classes ei + N, i = 1, ..., n, constitute a finite set of generators of M.

[only if] If x1, ..., xn generate M, then the R-linear map f : Rn → M defined by (a1, ..., an) ↦ a1x1 + · · · + anxn is surjective. Hence by the isomorphism theorem M ≅ Rn / Ker f.

**2.7.3. Algebras

Let be a homomorphism of rings. The ring A can be given an R-module structure with the multiplication map for and . This R-module structure of A is compatible with the ring structure of A in the sense that for every a, and x, one has (ax)(by) = (ab)(xy).

Conversely, if a ring A has an R-module structure with (ax)(by) = (ab)(xy) for every a, and x, , then there is a unique ring homomorphism taking a ↦ a · 1 (where 1 denotes the identity of A). This motivates us to define the following.

Definition 2.52.

Let R be a ring. An algebra over R or an R-algebra is a ring A together with a ring homomorphism . The homomorphism is called the structure homomorphism of the R-algebra A. If A and B are R-algebras with structure homomorphisms and ψ : R → B, then an R-algebra homomorphism (from A to B) is a ring homomorphism η : A → B such that .

Example 2.16.

Let R be a ring.

  1. The polynomial ring R[X1, . . . , Xn] is an R-algebra with the canonical inclusion as the structure homomorphism and is called a polynomial algebra over R.

  2. For an ideal of R, the canonical surjection makes an R-algebra.

  3. If A is an R-algebra with structure homomorphism and if B is an A-algebra with structure homomorphism ψ : A → B, then B is an R-algebra with structure homomorphism .

  4. Combining (2) and (3) implies that if A is an R-algebra and an ideal of A, then the ring is again an R-algebra, called the quotient algebra of A by .

An R-algebra A is an R-module with the added property that multiplication of elements of A is now legal. Exploiting this new feature leads to the following concept of algebra generators.

Definition 2.53.

Let A be an R-algebra with the structure homomorphism . A subset S of A is said to generate A as an R-algebra, if every element can be written as a polynomial expression in (finitely many) elements of S with coefficients from R (that is, from ). We write this as A = R[S]. If S = {x1, . . . , xn} is finite, we also write R[x1, . . . , xn] in place of R[S] and say that A is finitely generated as an R-algebra or that the homomorphism is of finite type.

Example 2.17.

  1. The polynomial algebra R[X1, . . . , Xn], n ≥ 1, over R is not finitely generated as an R-module, but is finitely generated as an R-algebra.

  2. For an ideal of R[X1, . . . , Xn], the ring is generated as an R-algebra by the equivalence classes of Xi, 1 ≤ i ≤ n, that is, A = R[x1, . . . , xn]. If is not the zero ideal, then A is not a polynomial algebra, because x1, . . . , xn are not indeterminates in the sense that they satisfy (non-zero) polynomial equations f(x1, . . . , xn) = 0 for every . (In this case, we also say that x1, . . . , xn are algebraically dependent.) The notation R[. . .] is a generalization of the notation for polynomial algebras. In what follows, we usually denote polynomial algebras by R[X1, . . . , Xn] with upper-case algebra generators, whereas for an arbitrary finitely generated R-algebra we use lower-case symbols for the algebra generators as in R[x1, . . . , xn].

One may proceed to define kernels and images of R-algebra homomorphisms and frame and prove the isomorphism theorem for R-algebras. We leave the details to the reader. We only note that algebra homomorphisms are essentially ring homomorphisms with the added condition of commutativity with the structure homomorphisms.

Theorem 2.32.

A ring A is a finitely generated R-algebra if and only if A is a quotient of a polynomial algebra (over R).

Proof

[if] Immediate from Example 2.17.

[only if] Let A := R[x1, . . . , xn]. The map η : R[X1, . . . , Xn] → A that takes f(X1, . . . , Xn) ↦ f(x1, . . . , xn) is a surjective R-algebra homomorphism. By the isomorphism theorem, one has the isomorphism A ≅ R[X1, . . . , Xn]/Ker η of R-algebras.

This theorem suggests that for the study of finitely generated algebras it suffices to investigate only the polynomial algebras and their quotients.

Exercise Set 2.7

2.63Let V be a K-vector space, U a subspace of V, and T an arbitrary K-basis of U. Show that there is a K-basis of V, that contains T. [H]
2.64

  1. Let V be a K-vector space, and U1, U2 subspaces of V. Show that the set is a K-subspace of V. If U1 ∩ U2 = {0}, we say that U is the direct sum of U1 and U2 and write U = U1 ⊕ U2.

  2. Let V be a K-vector space and W a subspace of V. Show that there exists a subspace W′ of V such that V = W ⊕ W′. This space W′ is called the complement subspace of W in V. [H]

2.65Let V and W be K-vector spaces and f : V → W a K-linear map. Show that f is uniquely determined by the images f(x), , where S is a basis of V.
2.66Let V and W be K-vector spaces. Check that HomK(V, W) is a vector space over K. Show that dimK(HomK(V, W)) = (dimK V)(dimK W). In particular, if W = K, then HomK(V, K) is isomorphic to V. The space HomK(V, K) is called the dual space of V.
2.67Let V and W be m- and n-dimensional K-vector spaces, S = {x1, . . . , xm} a K-basis of V, T = {y1, . . . , yn} a K-basis of W, and f : V → W a K-linear map. For each i = 1, . . . , m, write f(xi) = ai1y1 + · · · + ainyn, . The m × n matrix is called the transformation matrix of f (with respect to the bases S and T). We have:

Let V1, V2, V3 be K-vector spaces, f, f1, , and . Prove the following assertions:

  1. .

  3. .

  4. f is invertible (as a map) if and only if is invertible (as a matrix).

(Remark: This exercise explains that the linear transformations of finite-dimensional vector spaces can be explained in terms of matrices.)

2.68Show that for every there are integers a1, . . . , an that constitute a minimal set of generators for the unit ideal in . [H]
2.69Let M be an R-module. A subset S of M is called a basis of M, if S generates M and is linearly independent over R in the sense that , , , , implies a1 = · · · = an = 0. Show that M has a basis if and only if M is a free R-module.
2.70We define the rank of a finitely generated R-module M as

RankR M := min{#S | M is generated by S}.

If N is a submodule of M, show that RankR M ≤ RankR N + RankR(M/N). Give an example where the strict inequality holds.

2.71Let M be an R-module. An element is called a torsion element of M, if Ann Rx ≠ 0, that is, if there is with ax = 0. The set of all torsion elements of M is denoted by Tors M. M is called torsion-free if Tors M = {0}, and a torsion module if Tors M = M.

  1. Show that Tors M is a submodule of M.

  2. Show that Tors M is a torsion module (called the torsion submodule of M) and that the module M/Tors M is torsion-free.

  3. If R is an integral domain, show that every free module over R is torsion-free. In particular, every vector space is torsion-free.

2.72Show that:

  1. is not finitely generated as a -module. [H]

  2. is not a free -module. [H]

  3. is a torsion-free -module.

This shows that the converse of Exercise 2.71(c) is not true in general.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.
Reset
3.137.223.10