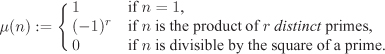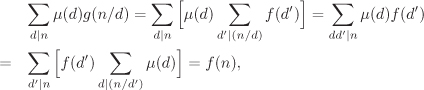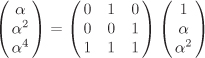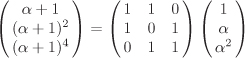2.9. Finite Fields

Finite fields are seemingly the most important types of fields used in cryptography. They enjoy certain nice properties that infinite fields (in particular, the well-known fields like , and ) do not. We concentrate on some properties of finite fields in this section. As we see later, arithmetic over a finite field K is fast, when char K = 2 or when #K is a prime. As a result, these two classes of fields are the most common ones employed in cryptography. However, in this section, we do not restrict ourselves to these specific fields only, but provide a general treatment valid for all finite fields. As in the previous section, we continue to use the letters F, K, L to denote fields. In addition, we use the letter p to denote a prime number and q a power of p: that is, q = pⁿ for some .

2.9.1. Existence and Uniqueness of Finite Fields

Let K be a finite field of cardinality q. Then p := char K > 0. By Proposition 2.7, p is a prime, that is, K contains an isomorphic copy of the field . If , we have q = pⁿ. Therefore, we have proved the first statement of the following important result.

Theorem 2.35.

Theorem 2.36. Fermat’s little theorem for finite fields

Theorem 2.37.

This uniqueness allows us to talk about the finite field of cardinality q (rather than a finite field of cardinality q). We denote this (unique) field by .

The results proved so far can be generalized for arbitrary extensions , where q = pⁿ, n, . We leave the details to the reader (Exercise 2.82). It is important to point out here that since is the splitting field of X^qm – X over , by Exercise 2.77 we have:

Corollary 2.14.

This implies that an irreducible polynomial has either none or all of its roots in . Also if with q = pⁿ, then α^q = α^pn = α. Therefore, α^pn–1 is a p-th root of α. By Exercise 2.76(b), we then conclude:

Corollary 2.15.

Proposition 2.34.

Corollary 2.16.

Theorem 2.38.

Theorem 2.39.

Corollary 2.17.

2.9.2. Polynomials over Finite Fields

In this section, we study some useful properties of polynomials over finite fields. We concentrate on polynomials in for an arbitrary q = pⁿ, , . We have seen how the polynomials X^qm – X proved to be important for understanding the structures of finite fields. But that is not all; these polynomials indeed have further roles to play. This prompts us to reserve the following special symbol: .

Let be a finite extension of finite fields and let be a root of the polynomial . Since each , we have . Therefore, . More generally, for each r = 0, 1, 2, · · · the element is a root of f(X). This gives us a nice procedure for computing the minimal polynomial of α as the following corollary suggests.

Corollary 2.18.

We now prove a theorem which has important consequences.

Theorem 2.40.

The first consequence of Theorem 2.40 is that it leads to a procedure for checking the irreducibility of a polynomial . Let d := deg f. If f(X) is reducible, it admits an irreducible factor of degree ≤ ⌊d/2⌋. Since is the product of all distinct irreducible factors of f with degrees dividing m, we compute the gcds g₁, . . . , g_⌊d/2⌋. If all these gcds are 1, we conclude that f is irreducible. Otherwise f is reducible. We will see an optimized implementation of this procedure in Chapter 3. Besides irreducibility testing, the above theorem also leads to algorithms for finding random irreducible polynomials and for factorizing polynomials, as we will also discuss in Chapter 3.

The second consequence of Theorem 2.40 is that it gives us a formula for calculating the number of monic irreducible polynomials of a given degree over a given field. First we need to define a function on .

Definition 2.58.

Lemma 2.6.

Lemma 2.7. Möbius inversion formula

Let us denote by ν_q,m the number of monic irreducible polynomials in of degree m and by the product of all monic irreducible polynomials in of degree m. By Theorem 2.40, we have and . Applications of the Möbius inversion formula then yield the following formulas:

Equation 2.4

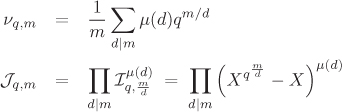
If p₁, . . . , p_r are all the prime divisors of m (not necessarily all distinct), Equation (2.4) together with the observation that μ(n) ≥ –1 for all imply that But each p_i ≥ 2, so that m ≥ 2^r, and hence . We, therefore, have an independent proof of the second statement in Corollary 2.17. Moreover, for practical values of q and m we have the good approximation:

Equation 2.5

Since the total number of monic polynomials of degree m in F_q[X] is q^m, a randomly chosen monic polynomial in of degree m has an approximate probability of 1/m for being irreducible, that is, one expects to get an irreducible polynomial of degree m, after O(m) random monic polynomials are picked up from . These observations have an important bearing for devising efficient algorithms for finding irreducible polynomials over finite fields. (See Chapter 3.)

The conjugates of over are α^qi, . It is interesting to look at the sum and the product of the conjugates of α. By Corollary 2.18, for some . Since , the elements and belong to . Since α^qd = α, for any (positive) integral multiple δ of d, the sum and the product are elements of too.

Definition 2.59.

The trace and norm functions play an important role in the theory of finite fields. See Exercise 2.86 for some elementary properties of these functions.

2.9.3. Representation of Finite Fields

is a vector space of dimension m over . Let β₀, . . . , β_m–1 be an -basis of . Each element has a unique representation a = a₀β₀ + · · · + a_m–1β_m–1 with each . Therefore, if we have a representation of the elements of , we can also represent the elements of . Thus elements of any finite field can be represented, if we have representations of elements of prime fields. But the set {0, 1, . . . , p – 1} under the modulo p arithmetic represents .

So our problem reduces to selecting suitable bases β₀, . . . , β_m–1 of over . In order to illustrate how we can do that, let us choose a priori a fixed monic irreducible polynomial with deg f = m. We then represent , where α (the residue class of X) is a root of f in . The elements are linearly independent over , since otherwise we would have a non-zero polynomial of degree less than m, of which α is a root. The -basis 1, α, . . . , α^m–1 of is called a polynomial basis (with respect to the defining polynomial f). The elements of are then polynomials of degrees < m. The arithmetic in is carried out as the polynomial arithmetic of modulo the irreducible polynomial f.

Example 2.19.

Polynomial bases are most common in finite field implementations. Some other types of bases also deserve specific mention in this context.

Definition 2.60.

It can be shown that normal bases exist for all finite extensions . It can even be shown that primitive normal bases also do exist for all such extensions.

Example 2.20.

Computations over finite fields often call for exponentiations of elements a = a₀β₀ + · · · + a_m–1β_m–1. If β_i = α^qi, i = 0, . . . , m – 1, construct a normal basis, , since α^qm = α and for each i. Thus the coefficients of a^q (in the representation under the given normal basis) is obtained simply by cyclically shifting the coefficients a₀, . . . , a_m–1 in the representation of a. This leads to a considerable saving of time. In particular, this trick becomes most meaningful for q = 2 (a case of high importance in cryptography).

Now that exponentiations become cheaper with normal bases, one should not let the common operations (addition and multiplication) turn significantly slower. The sum of a = a₀β₀ + · · · + a_m–1β_m–1 and b = b₀β₀ + · · · + b_m–1β_m–1 continues to remain as easy as in the case of a polynomial basis, namely, a + b = (a₀ + b₀)β₀ + · · · + (a_m–1 + b_m–1)β_m–1, where each a_i + b_i is calculated in . However, computing the product ab introduces difficulty. In particular, it requires the representation of β_iβ_j, 0 ≤ i, j ≤ m – 1, in the basis β₀, . . . , β_m–1, say, . For i ≤ j, we have . It is thus sufficient to look only at the coefficients , 0 ≤ j, k ≤ m – 1. We denote by C_α the number of non-zero . From practical considerations (for example, for hardware implementations), C_α should be as small as possible. For q = 2, one can show that 2m – 1 ≤ C_α ≤ m². If, for this special case, C_α = 2m – 1, the normal basis α, α^q, . . . , α^qm–1 is called an optimal normal basis. Unlike normal (or primitive normal) bases, optimal normal bases do not exist for all values of .

We finally mention another representation of elements of a finite field , that does not depend on the vector space representation discussed so far, but which is based on the fact that the group is cyclic. If we are given a primitive element (that is, a generator) γ of , then the elements of are 0, 1 = γ⁰, γ, . . . , γ^q–2. Multiplication and exponentiation become easy with this representation, since 0 · a = 0 for all , whereas γⁱ · γ^j = γ^k with k ≡ i + j (mod q – 1). Unfortunately, this representation provides no clue on how to compute γⁱ + γ^j. One possibility is to store a table consisting of the values z_k satisfying 1 + γ^k = γ^z_k for all k = 0, . . . , q – 2 (with γ^k ≠ –1), so that for i ≤ j one can compute γⁱ + γ^j = γⁱ(1 + γ^j–i) = γⁱγ^z_j–i = γ^l, where l ≡ i + z_j–i (mod q – 1). Such a table is called Zech’s logarithm table, can be maintained for small values of q and may facilitate computations in extensions . But if q is large (or more correctly if p is large, where q = pⁿ), this representation of elements of is not practical nor often feasible. Another difficulty of this representation is that it calls for a primitive element γ. If q is large and the integer factorization of q – 1 is not provided, there are no efficient methods known for finding such an element or even for checking if a given element is primitive.

Example 2.21.

Table 2.4. Zech’s logarithm table for with respect to γ = β + 1

k	γk	1 + γk	zk
0	1	2	4
1	β + 1	β + 2	7
2	2β	2β + 1	3
3	2β + 1	2β + 2	5
4	2	0	–
5	2β + 2	2β	2
6	β	β + 1	1
7	β + 2	β	6

Exercise Set 2.9

2.80	Let F be a field (not necessarily finite) of characteristic and let a, . Prove that (a + b)p = ap + bp, or, more generally, (a + b)pn = apn + bpn for all . [H]
2.81	Let , and q := pn. Prove that: If , then f(Xp) = f(X)p. If , then f(Xp) = g(X)p for some .
2.82	Let , n, and q := pn. Let F ⊆ K be an extension of finite fields with #F = q and #K = qm. Show that K is the splitting field of over . [H]
2.83	Write the addition and multiplication tables of (some representations of) the fields and . Use these tables to find a primitive element in each of these fields and a normal element in (over ).
2.84	Let K be a field (not necessarily finite or of positive characteristic). Let be of degree 2 or 3. Prove that f is reducible in K[X] if and only if f has a root in K. Deduce that X2 + X + 1 and X3 + X + 1 are irreducible in . Let be of degree d ≥ 0. The opposite of f is the polynomial . Show that f(X) is irreducible in K[X] if and only if fop(X) is irreducible in K[X]. Deduce that X3 + X2 + 1 is irreducible in .
2.85	In this exercise, one studies the arithmetic in the finite field . Show that is irreducible. Let us represent as . Call and consider the elements a := 3α2 + 2α + 1 and b := 2α2 + 3 in . Compute ab–1 in this representation of . You should compute the canonical representative of ab–1 in , that is, a polynomial in α of degree < 3 with coefficients reduced modulo 5.
2.86	Let F ⊆ K ⊆ L be finite extensions of finite fields with [L : K] = s. Let α, and . Prove the following assertions: TrK|F(α + β) = TrK|F(α) + TrK|F (β) and NK|F (αβ) = NK|F (α) NK|F (β). TrL|F (α) = s TrK|F (α) and NL|F (α) = NK|F (α)s. Transitivity of trace and norm TrL|F (γ) = TrK|F (TrL|K(γ)) and NL|F (γ) = NK|F (NL|K (γ)).
2.87	Let be a finite extension of finite fields. In this exercise, we treat both K and L as vector spaces over K. Show that: TrL|K is a surjective linear transformation L → K. All the linear transformations L → K are given by Tα : L → K, β ↦ TrL|K(αβ), where . (In this notation, TrL|K = T1.) Moreover, for distinct elements α, the linear transformations Tα and Tα′ are distinct.
2.88	Let K and L be as in Exercise 2.87 and let . Show that TrL|K(β) = 0 if and only if β = γq – γ for some .
2.89	Let K and L be as in Exercise 2.87. Two K-bases (β0, . . . , βm–1) and (γ0, . . . , γm–1) of L are called dual or complementary, if TrL|K(βiγj) = δij.[10] Show that every K-basis of L has a unique dual basis. [10] The Kronecker delta δ on an index set I (finite or infinite) is defined for i, as:
2.90	Prove that every finite extension of finite fields is Galois. [H]
2.91	For the extension , consider the map , α ↦ αq. Show that is an -automorphism of . is called the Frobenius automorphism of over . Show that is cyclic of order m and with as a generator. [H]
2.92	Let be irreducible with deg f = d. Consider the extension and let r := gcd(d, m). Show that f is irreducible in if and only if r = 1. [H] More generally, show that f factors in into a product of r irreducible polynomials each of degree d/r.
2.93	Consider the representation of in Example 2.19. Construct the minimal polynomials over of the elements of . [H]
2.94	Show that the number of (ordered) -bases of is (qm – 1)(qm – q)(qm – q2) · · ·(qm – qm – 1).