B.7. Matrix-based Key Predistribution

The matrix-based key predistribution scheme is derived from the idea proposed by Blom [25]. It is similar to the polynomial-based key predistribution and employs symmetric matrices (in place of symmetric polynomials). Let be a finite field with q just large enough to accommodate a symmetric key and let G be a t × n matrix over , where t is determined by the memory of a sensor node and n is the number of nodes in the network. It is not required to preserve G with secrecy. Anybody, even the enemies, may know G. We only require G to have rank t, that is, any t columns of G must be linearly independent. If g is a primitive element of , the following matrix is recommended.

Equation B.10

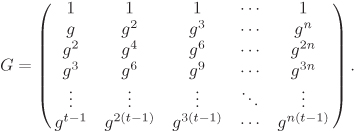
In a memory-starved environment, this G has a compact representation, since its j-th column is uniquely identified by the value g^j. The remaining elements in the column can be easily computed by performing few multiplications.

Let D be a secret t × t symmetric matrix, and A the n × t matrix defined by:

A := (DG)^t = G^tD^t = G^tD.

Finally, define the n × n matrix

K := AG.

It follows that K = AG = G^t DG = G^t (G^t D^t)^t = G^t (G^t D)^t = G^t A^t = (AG)^t = K^t, that is, K is a symmetric matrix. If the (i, j)-th element of K is denoted by k_ij, we have k_ij = k_ji, that is, this common value can be used as a pairwise key between the i-th and j-th nodes.

Let the (i, j)-th element of A be denoted by a_ij for 1 ≤ i ≤ n and 1 ≤ j ≤ t. Also let g_ij, 1 ≤ i ≤ t and 1 ≤ j ≤ n, denote the (i, j)-th element of G. But then the pairwise key k_ij = k_ji is expressed as:

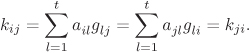
Thus, the i-th row of A and the j-th column of G suffice for the i-th node to compute k_ij. Similarly, the j-th row of A and the i-th column of G allow the j-th node to compute k_ji. In view of this, every node, say, the i-th node, is required to store the i-th row of A and the i-th column of G. If G is as in Equation (B.10), only gⁱ needs to be stored instead of the full i-th column of G. Thus, the storage of t + 1 elements of (equivalent to t + 1 symmetric keys) suffices.

During direct key establishment, two physical neighbours exchange their respective columns of G for the computation of the common key. Since G is allowed to be a public knowledge, this communication does not reveal secret information to the adversary.

Suppose that the adversary gains knowledge of some t′ ≥ t rows of A (say, by capturing nodes). We also assume that the matrix G is completely known to the adversary. The adversary picks up any t known rows of A and constructs a t × t matrix A′ comprising these rows. But then A′ = G′D, where G′ is a suitable t × t submatrix of G. Since G is assumed to be of rank t, G′ is invertible and so the secret matrix D can be easily computed. Conversely, if D is known to the adversary, she can compute A and, in particular, any t′ ≥ t rows of A.

If only t′ < t rows are known to the adversary, then any choice of any t – t′unknown rows of A yields a value of the matrix D, and subsequently we can construct the remaining n–t unknown rows of A. In other words, D cannot be uniquely recovered from a knowledge of less than t rows of A. This task is difficult too, since there is an infeasible number of choices for assigning values to the elements of the unknown t – t′rows of A.

To sum up, the matrix-based key predistribution scheme is completely secure, if less than t nodes are only captured. On the other hand, if t or more nodes are captured, then the system is completely compromised. Thus, the resilience against node capture of this scheme is determined solely by t and is independent of the size n of the network. The parameter t, in turn, is restricted by the memory of a sensor node (a node has to store t + 1 elements of ).

In order to overcome this difficulty, Du et al. [79] propose a matrix-pool-based scheme. Here, S matrices A₁, A₂, . . . , A_S are computed from S pairwise different secret matrices D₁, D₂, . . . , D_S. The same G may be used for all these key spaces. Each node is given shares (that is, rows) of s matrices randomly chosen from the pool {A₁, A₂, . . . , A_S}. The resulting details of the matrix-pool-based scheme are quite analogous to those pertaining to the polynomial-pool-based scheme described in the earlier section, and are omitted here.