CHAPTER 7
Time Value and Decay
Option expiration and the resulting regular decay in value set options apart from nearly every other financial vehicle. Options are a wasting asset and as such the time value, meaning the value of the luxury of waiting to make a decision, will go toward zero as expiration approaches. At expiration this time value becomes zero, you don’t have the luxury of waiting any longer to make up your mind.
Every option is a contest between value, which is volatility in the underlying asset, and price, which is really just the accumulated time decay. That battle between erosion and volatility means that the two factors offset each other. If volatility helps your option position, even if it’s movement in a particular direction, then the passage of time and the resulting decay generally hurt your position. For example, if you’re long the at-the-money call option, then you want movement to the upside and you want a ton of it, the more the better. But if you’re long that call option, then the passage of time is your enemy because the price of that option will erode. If you need time to fly then you want the market to sit. If you need the market to move then you want time to stand still.
Option traders have to be careful how they talk about time decay. The entire value of an option doesn’t decay; it’s only the time value of the option that erodes. The inherent value, that is the value by which the option is in-the-money, will never erode; if an option is worth $1.75 and is in-the-money by $1.00, then $0.75 of that option value is pure time value. It’s that $0.75 that’s going to erode.
Many option traders make the mistake of only thinking of option prices in terms of the total premium paid or received. They paid $3.00 for an option, so they think that is the cost. But option traders would do better by thinking of the daily decay in option prices as the real price of an option—it’s the price the option owner pays for being long that option for that day, and it’s the price the option seller expects to receive for bearing the risk in being short that option for that day. It is that day’s rent paid or received for having or giving the luxury of waiting. Thinking of option prices in discrete days also helps traders remember that they are only long or short from the previous day’s closing price, and that you always have the right to make a more informed trade.
TIME VALUE BY STRIKE PRICE
As we saw in Chapter 1, time value is greatest for an option that is at-the-money, and time value trails off as we get further from at-the-money. How quickly does time value trail off? Let’s look at some hypothetical 30-day options and keep all variables fixed with the exception of strike price. (See Table 7.1.)
Table 7.1 Time Value by Strike Price
| Strike Price | Option Time Value |
| 92 | 0.00 |
| 93 | 0.01 |
| 94 | 0.02 |
| 95 | 0.04 |
| 96 | 0.10 |
| 97 | 0.21 |
| 98 | 0.40 |
| 99 | 0.71 |
| 100 | 1.14 |
| 101 | 0.71 |
| 102 | 0.40 |
| 103 | 0.21 |
| 104 | 0.10 |
| 105 | 0.04 |
| 106 | 0.02 |
| 107 | 0.01 |
| 108 | 0.00 |
The graph in Figure 7.1 is very similar to the graph we saw in Figure 1.7.
FIGURE 7.1 Time Value by Strike Price
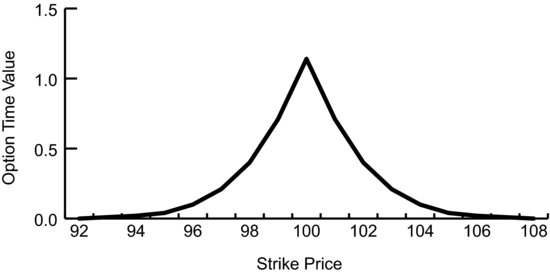
The curve is the time value by strike price for 30-day options. Time value is at its maximum of 1.14 for the at-the-money strike price. It falls as the strike prices become further from at-the-money until the time value becomes zero, or very nearly zero; the time value of an extremely out-of-the-money strike price is very close to zero. For our purposes it is zero because it’s likely to be less than the minimum price at which the option can trade. Decay affects only the time value portion of an option price, and time value is greatest for at-the-money options. It follows that daily decay is greatest for at-the-money options and trails off as we move away from at-the-money just as total time value does. This makes sense because the time value for all options is going to zero. If the at-the-money option has furthest to go by expiration, then it has to go fastest in order to get there.
Two of these options, the 92 strike put and the 108 strike call, effectively have zero time value. What would the time value of those same options (i.e., options with the same strike price) be if they had ninety days to expiration? They would almost certainly have some time value. Zero time value to some time value would be quite an increase. Would an at-the-money option that’s about to expire and which still has a little time value see the same sort of increase in time value if we extended the expiration to 90 days?
THETA—THE MEASURE OF DAILY OPTION TIME VALUE EROSION
We know that at-the-money options will erode faster than out-of-the-money options because they have further to go to get to zero but have the same amount of time as any other option with that expiration date. Other than that, we know when our option is going to expire, we know what we’re paying/receiving for our option, so why care about other issues surrounding decay other than it being the day’s measure of what the buyer expects to pay and what the seller expects to collect? I divide my option price by days to expiration and, bingo, I know what my option is going to cost/pay me today, right? Let’s see, using the following numbers.
If we divided that $8.00 price by 90 days to expiration we get 0.089, so we might expect the daily erosion of that option to be 0.089.
We can calculate the expected price erosion by using an option pricing model like the one at OptionMath.com. The formula for this calculation can be found in the Appendix. Using this pricing model we learn that the model expects the daily erosion to be 0.045. Why is there such a difference? The “straight line” erosion is double that generated by the model. Which one is correct? Is there a way to take advantage of this discrepancy?
With, say, 90 days to expiration the erosion of time value for an at-the-money option is obviously finite. Even if we don’t know precisely what the erosion should be, we know the option isn’t going to be worthless, all else being equal, when we wake up the next day with 89 days left to expiration. Yet on the day of expiration the rate of decay is infinite; when we woke up on expiration morning the time value of the option was positive, maybe not by much but it was positive. At the moment of expiration the time value becomes zero. The rate of erosion, for example the erosion we’d expect each day, seems to increase, moving from finite to infinite on the day of expiration. This would be why the linear erosion assumption of 0.089 daily differs from the result of 0.045 generated by the model. It seems that erosion may speed up, buy why?
OPTION PRICE EROSION DOESN’T HAPPEN IN A STRAIGHT LINE
It seems that option price erosion may speed up, but it also seems logical that option prices may erode in a straight line as time passes. So which is it, and why?
Option price erosion doesn’t happen in a straight line. Why? Because return is a function of time, and risk is a function of the square root of time. The result is that erosion for an at-the-money option increases exponentially.
Let’s see how this works out with our previous example, but let’s change the numbers slightly.
What if all the option specifics we used in the samples remain constant except for time to expiration, which decreases to 30 days? Our option pricing model tells us that call option is worth $4.60 (since it’s at-the-money all of the price represents time value) and our option pricing model tells us the price of this call option will erode by $0.077 that day. The first proof that the model is correct and that erosion doesn’t happen in a straight line is that the price of our 30-day option isn’t one third of the price of our 90-day option.
What if we’re really close to expiration? All the other option specifics remain constant but there’s only five days to expiration? We’d expect that call option to be worth $1.87, and we expect the price to erode by $0.188 that day.
Because of the option math and the nature of risk, time value does not erode in a straight line. Erosion gets faster as time passes and eventually moves very fast becoming essentially infinite at the moment of option expiration, when time value goes from something to nothing. Putting our examples into an option pricing model confirms that erosion changes, it accelerates as time passes and expiration nears.
If we were to calculate the expected daily erosion for every day, all else being equal, we’d find that the expected erosion is actually exponential.
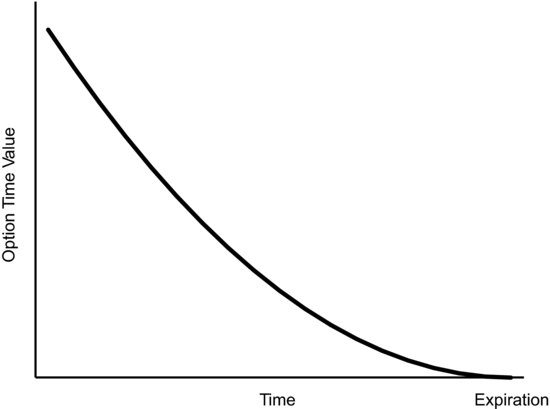
As we see in Table 7.2,the daily erosion is initially relatively small. The erosion each day is a little bit greater than it was the day before and it is a little bit less than it will be tomorrow. It increases exponentially until at the moment of expiration the erosion is infinite. The important point is that at-the-money options erode faster as expiration nears. Figure 7.2 shows what the typical time value erosion would look like for an at-the-money option.
Table 7.2 Expected Time Value Erosion by Expiration, At-the-Money Option
| Days to Expiration | Theoretical Option Value | Expected Daily Price Erosion |
| 90 | 8.00 | 0.045 |
| 60 | 6.52 | 0.055 |
| 30 | 4.60 | 0.077 |
| 20 | 3.75 | 0.094 |
| 10 | 2.65 | 0.133 |
| 5 | 1.87 | 0.188 |
FIGURE 7.2 Typical Erosion for an At-the-Money Option

Erosion doesn’t happen in a straight line because of the relationship between the math of reward and the math of risk, but that doesn’t mean erosion happens the same for all options. We see in Figure 7.2 the half-parabola shape for at-the-money options. Given that the relationship between time and risk is different for an out-of-the-money option, what would that erosion graph look like? Figure 7.3 is the typical graph of the time value erosion for an out-of-the-money option.
FIGURE 7.3 Option Price Erosion for an Out-of-the-Money Option
Most of the erosion of out-of-the-money options occurs earlier in their term. Eventually there’s no time value to erode away. The important point for the option trader is that far out-of-the-money options erode more slowly as expiration nears but they’re eroding from a very cheap price because the bulk of the time value has already come out of the option price.
For these exercises our use of the terms at-the-money and out-of-the-money are relative. If the underlying stock is at $99.95, then the 100 call is technically out-of-the-money but we’d expect it to act pretty much like an at-the-money option. In fact, most option traders would say the 100 call is the at-the-money call option in that situation.
Don’t think that these erosion relationships change drastically if the price of the underlying stock changes by a small amount. These relationships change gradually. But this difference in the timing and rates of erosion is a phenomenon we can exploit using calendar spreads, as we’ll see in Part Three.
OPTION PRICE EROSION, THE WHAT
Option price erosion is purely a function of the fact that options are wasting assets. The expected option price erosion (theta) is purely a function of the option math. Unlike some other important measures like option skew, which we discussed in Chapter 6, option price erosion isn’t a function of the underlying asset. All options will erode and are expected to do so without regard to factors outside the option math. Now this doesn’t mean that the actual option price changes we experience will equal what is expected, even from an option pricing model; in those cases there are other factors at work. Generally, implied volatility will have changed.
The starting points on Figure 7.2 and Figure 7.3, the prices of the option and the expected daily price change due to erosion, will change with changes in implied volatility, but the general shape of the curves won’t change.
But this raises the question: How much does implied volatility impact the rate of option price erosion for an at-the-money option? How does that curve we saw in Figure 7.1 change with different levels of implied volatility? Let’s assume all the other variables are unchanged and the option has 30 days to expiration.
The erosion as a percentage of option price decreases slightly as implied volatility increases as we see in Table 7.3, but the impact is minimal and is largely a function of compounding. Table 7.4 shows erosion for an out-of-the-money option.
Table 7.3 Expected Option Price Erosion by Implied Volatility, At-the-Money Option

Table 7.4 Expected Option Price Erosion by Implied Volatility, 10% Out-of-the-Money
| Implied Volatility | Theoretical Option Value | Expected Daily Price Erosion |
| 5% | 0.01 | 0.000 |
| 10% | 0.06 | 0.002 |
| 20% | 0.98 | 0.015 |
| 50% | 6.21 | 0.054 |
| 100% | 16.05 | 0.111 |
| 200% | 35.20 | 0.204 |
It’s not important for the retail option trader to be able to calculate this daily erosion, particularly for directional trades, but it’s vital to understand that erosion isn’t linear; for an at-the-money option or a just out-of-the-money option it speeds up as expiration nears. A 30-day option is going to erode more tomorrow in dollar terms than an otherwise identical 60-day option will. It’s also vital to understand that there are trades and structures that take advantage of it and trades and structures that are really punished by it.
ANOTHER WAY OF LOOKING AT DAILY EROSION
It’s easy to get wrapped up in the actual erosion of options because that’s what we see on our screen or in our brokerage statement. The expected daily erosion is generally once removed from our experience. We have to calculate it and even if we actually see it, then it’s only as the difference between what the option was worth yesterday and what it’s worth today. Figure 7.4 shows in sharp relief how the theta of an at-the-money option and an out-of-the-money option will change with time to expiration.
FIGURE 7.4 Changes in Theta Over Time
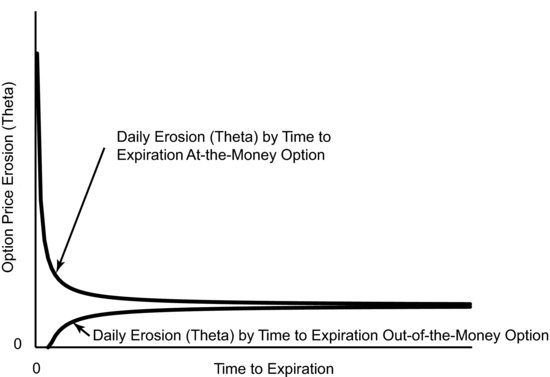
The important lesson to be gleaned from Figure 7.4 is that erosion will increase exponentially for an at-the-money option eventually becoming infinite at the moment of expiration. For an option that is far enough out-of-the-money the phenomenon of erosion works differently near expiration. Nearly all of the time value will have already been wrung out of the option price leaving it very close to zero. This being the case, that there’s little time value to erode away, theta will actually decline as expiration nears. In this situation there is little use in selling an out-of the-money option if it’s so near expiration that erosion is slowing.

- Time value of an option is greatest when that option is at-the-money.
- The time value of the at-the-money option erodes more quickly as time passes until the erosion becomes infinite at the moment of expiration.
- The time value of an out-of-the-money option will erode more slowly as time passes when the option is close to expiration. This is due to the fact that most of the time value will have already disappeared for an out-of-the-money option.
