CHAPTER 8

The Bid/Ask Spread

The bid/ask spread is how market makers make their money, and some of them have made a ton of it.

Everyone who’s traded stock or options knows that the last traded price is just the beginning. When it’s actually time to execute a trade you’re faced with two prices, the bid price and the ask price (sometimes called the offer or offer price). The bid price is the price that the market is bidding for your stock or option. It is the price the market is willing to pay you for your stock or for options if you want to sell. If you wanted to sell a single share or option immediately, then you’d expect to receive the bid price.

The ask price is the price that the market is asking for in order to sell you stock or options. It is the price the market is willing to accept in exchange for selling your stock or option to you. If you wanted to buy a single share or option immediately, then the ask price is the price you’d expect to pay. Think of the bid price as the wholesale price, think of the ask price as the retail price.

WHAT DO WE MEAN BY “THE MARKET”?

When we refer to “the market” we really mean the combination of all the market participants. There might be market makers, high-frequency traders, hedge funds, and long-term investors who are willing to pay the bid price. The bid you see on your screen is generated by all those who have entered limit orders saying that they’re willing to pay that bid price (but no more) in order to buy this stock or option. You could join this bid by placing a limit order to buy at that price. You may get your limit order filled, that is, you may buy the stock at that price, or you may not see your order filled. You’ll get your limit order to buy filled only if someone is willing to sell to you at that price. It may be just a single order or a few orders willing to sell at that bid price, in which case the few buyers are selected by the exchange through an algorithm that may take into account when the buy order was entered, market-maker status (and hence market-maker responsibility to the market), size of the order, and other factors. It may turn out that the market in general decides that the stock or option is worth less than the bid price, in which case all of the bids at that price will be filled.

The bid may be composed of a single limit order for only a few shares, or it might be composed of many separate limit orders representing many thousands of shares. Sophisticated data feeds will tell you the total number of shares or options bid for at that price, as well as the number of separate orders bidding at that price.

The same is true for the ask price. A market maker may be willing to sell at the ask while a long-term investor may be willing to sell stock owned for decades at that same ask price. Again, you can join this offer by placing a limit order to sell at that price. Many different types of market participants are likely to have offers to sell the stock or option at that ask price.

It’s not only possible but it’s likely that the same trader or market maker is willing to both pay the bid price and sell at the ask price and simultaneously has orders entered to accomplish both. These true market makers are happy to buy at the bid price in the expectation that they might later sell at the ask price in order to close their position. They’d be nearly as willing (more on why they wouldn’t be just as willing later) to first sell at the ask price in the expectation that they’ll later pay the bid price to close their position. The difference is their hoped-for profit. That profit is likely to be small in absolute terms for each transaction but multiply by thousands or hundreds of thousands of such trades each day, and market makers can generate significant profit. The risk to market makers is that the market will move against them before they are able to close out their position, resulting in a loss.

True market makers provide liquidity by serving as willing buyers to sellers and by serving as willing sellers to buyers. The bid/ask spread is the compensation for this service. Market makers are an important element in any well-functioning market. Imagine you wanted to buy a particular, not very commonly traded, option. If there were no market makers willing and able to take the risk of selling that option to you (and in the process, put their own money at risk), you’d have to wait until someone else needed to sell that exact option. Even then there is no assurance that the difference between the price you’re willing to pay and the price they’re willing to accept wouldn’t be insurmountable. And we haven’t even addressed the fact that you might want to buy ten options and they might only have three options to sell.

Just because market makers are an important part of the landscape doesn’t mean we have to donate to their livelihood. Smart traders will try to diminish the bite the bid/ask spread takes out of trading profits. Really smart traders will try to put the bid/ask spread to their advantage.

MARKET MAKERS

The term market maker, in both the equity and option worlds, actually refers to several different types of traders doing several different things.

Some market makers are lead market makers, meaning they have certain advantages but also have certain responsibilities. On the New York Stock Exchange they’re called Designated Market Makers (DMMs), and they’ve replaced the old specialists. Like those old specialists, DMMs have the responsibility of maintaining a fair and orderly market in their stocks. On option exchanges like the International Securities Exchange (ISE), one of the biggest option exchanges in the world, the lead market makers are called Primary Market Makers (PMMs). PMMs continuously post bids and offers in all of the options for which they are designated and have responsibility for maintaining fair and orderly markets.

Other market makers have less responsibility and may simply use technology to stream bids and offers for most of the options on selected underlyings. For example, at the ISE, these are referred to as Competitive Market Makers (CMMs) or Electronic Access Members (EAM).

Generally these market makers will post a bid price, the price they’re willing to pay, and an ask price, the price at which they’re willing to sell, for each option on the underlying stocks they follow. Again, this is done with limit orders. Years ago this interaction was accomplished face to face. Options on each underlying stock were traded at a particular post on the exchange floor. The lead market maker or a broker would request a quote, meaning both a bid and an offer, from the “crowd” that traded the options at that post. The broker would request both a bid and an offer, even if he knew he had an order to sell these options, in an effort to force the assembled traders to provide prices that are as close as possible to fair value. The assembled traders would consult trading sheets that listed every option and its value for every potential underlying price. If the assembled traders all independently thought the option was worth approximately $3.10 (some might think it’s worth $3.08, some might think it’s worth $3.12, some might think it’s worth something in between but all are going to believe that the option is worth about $3.10—if some of them thought it was worth significantly more or less than that then they’d end up trading among themselves until the price had reached equilibrium), then they might collectively bid $3.00 and offer it at $3.20. Now imagine that the broker comes into the pit and asks for only a bid for this option. He’s tipped his hand that he’s likely a seller. The assembled traders, knowing that the broker is likely to be a seller, might bid $2.75. They would not even have to offer the option for sale.

Today, this bidding and offering is done instantaneously and electronically. Today’s market makers input general parameters into trading computers, which automatically transmit bids and offers for each option for a specific underlying stock. If the price of the stock moves, even if it moves by only a penny, the trading computer will recalculate its bids and offers for all the options on that stock, cancel those that are no longer valid, and post new bids and offers.

BID/ASK SPREAD, THE WHAT

Table 8.1 shows actual bids and offers for some options on SPY, the S&P ETF. There were 15 days to expiration and the SPY market was 132.56 bid, 132.57 ask, 132.57 last trade.

Table 8.1 SPY Option Bids and Offers

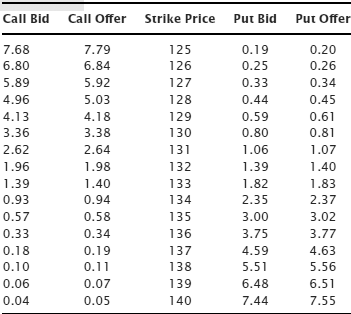
Just a cursory look at these numbers generates some interesting questions. Why is the spread between bid and ask so large for in-the-money options if it’s so small for out-of-the-money options with the same strike price? The spread is only $0.01 for many of these out-of-the-money options. Since that’s as small as it can get I’m agnostic as to which option I trade, at least in terms of the bid/ask spread, right? Other questions arise: What do these bids and offers say about the “fair value” of any particular option? Given these prices, what kind of order should I execute, and if I enter a limit order what should my limit price be? There are many others but we’ll begin with these.

As we’ve discussed, the true cost of an option, the apples-to-apples comparison price, is implied volatility. If we took these prices and generated implied volatilities, what would we get? Table 8.2 shows the bids and offers from Table 8.1 translated into implied volatilities assuming that the SPY price was the last traded price, $132.57. Remember that implied volatility is a percentage and we’ve removed the “%” sign—just as we’ve removed the “$” sign from the option prices in Table 8.1 to make the table clearer.

Table 8.2 SPY Option Bids and Offers by Implied Volatility

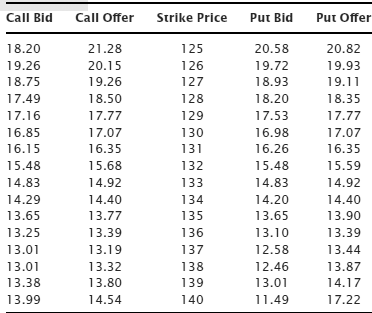
Things look a little different when viewed in terms of implied volatility. Among the call options the smallest bid/ask spread is at the 133 strike where the spread is only 0.09 volatility points (14.92 – 14.83). That is also the smallest spread as a percentage of the volatility. It’s less than 1 percent of the volatility at that strike (0.09/14.83). It’s no accident that the option with the smallest bid/ask spread in volatility terms is the first option from at-the-money (132.57) to have a $0.01-wide spread. From there the spread remains $0.01 wide in dollar terms but continues to increase in volatility terms. This increase is merely a function of the fact that the spread can’t get smaller in dollar terms, but as an option gets further out-of-the-money and decreases in price that $0.01 represents a bigger difference in implied volatility. Figure 8.1 shows a graph of the bid/ask spread of SPY in terms of volatility.

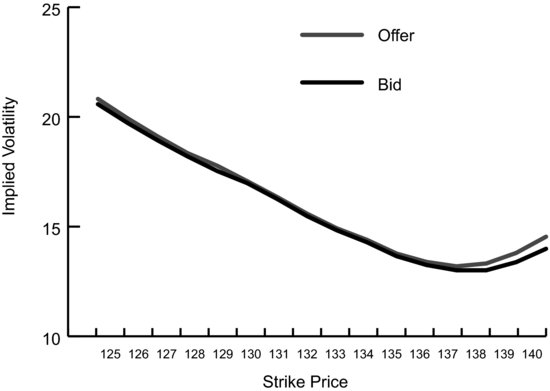
Looking at Figure 8.1 it’s easy to see that the true bid/ask spread, the spread between the bid implied volatility and the ask implied volatility, is relatively narrow for all strike prices. The absolute range in implied volatility across all strike prices makes viewing Figure 8.1 difficult for at-the-money strike prices. Figure 8.2 shows bids and offers by implied volatility for a smaller range of strike prices.

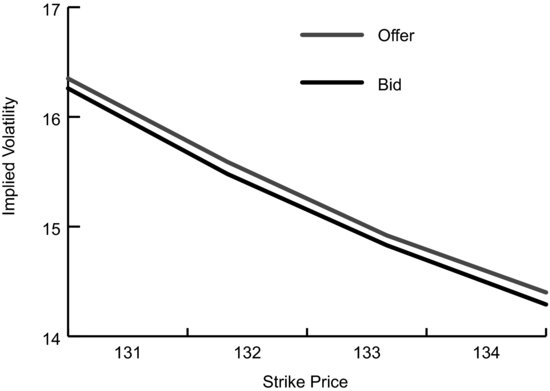
You’ve probably noticed that the spread for deep-in-the-money options is big in both dollar and volatility terms. The dollar spread for the 125 calls is $0.11 and the volatility spread is over 3.00 volatility points, even though the dollar spread for the 125 puts is only $0.01 and the volatility spread is only 0.24 volatility points. Why is that? First, there’s very little trading of deep-in-the-money options like the 125 calls in this situation. That means that there’s very little need for market makers to compete for trades. If they don’t need to compete, they don’t need to improve their markets by increasing their bid and/or reducing their offer.

DELTA’S IMPACT ON BID/ASK SPREADS

A more compelling issue for market makers bidding and offering those 125 strike calls is delta hedging. Option market makers seek to strip the directionality out of their trades and thereby turn them into volatility-based positions. They do this by delta hedging their options. They would do this in the case of these 125 strike calls by selling SPY shares if they were buyers of the calls and by buying SPY shares if they were sellers of the calls. They would hedge using SPY in an amount that would offset the directionality of the position. That amount is the delta of the option we discussed in Chapter 4.

The same option pricing model that generated these implied volatilities tells us that the delta of these 125 calls is 93. The 125 calls will move by 93 percent of the amount the SPY does. This means our market maker would have to execute 93 shares of SPY for each call option traded. Seen in this light it’s obvious that the width of the bid/ask spread in the underlying becomes an issue for the option market maker. How big an issue is it?

Instead of calculating these implied volatilities using the last traded price for SPY, as we’ve done so far, what would we get if we calculated the implied volatility of the option’s bid versus the bid of SPY? This would represent the effective implied volatility an option market maker would pay in buying the call on the bid and hedging by selling the underlying SPY on the bid. If we did that we’d find that the bid in implied volatility terms is actually 18.50. We might do the same thing using the call offer price and the SPY offer price. This would represent selling the call at the offer and paying the offer for SPY ($132.57) to delta hedge the option position and strip the short-term directionality out of the trade. But we don’t need to do this separately. We calculated these original implied volatilities assuming that SPY was at $132.57 because that was the last traded price. Thus, those original implied volatilities represent the “offered” implied volatility. That bid/ask spread in implied volatility terms (18.50/21.28) is better, but it’s still pretty wide. It’ll stay wide because there’s no incentive for the market to improve the spread, and that wide spread is necessary to compensate the market maker for the risk inherent in having to hedge by buying or selling a bunch of shares of SPY.

In an underlying with a very active, liquid option market like SPY, directional traders don’t have to pay too much attention to the real bid/ask spread for options that are at-the-money or close to at-the-money because the money spread is only $0.01, as small as it can get, and the result is that the volatility spread is pretty small too. It’s as small as it can get as long as $0.01 is the minimum price increment for the option.

WIDER BID/ASK SPREADS

What about options that don’t have $0.01-wide bid/ask spreads? This might be the case because the underlying is much more expensive. In that case the options have to be much more expensive, meaning a small bid/ask in implied volatility terms will generate wider spreads in dollar terms. Let’s do this comparison by looking at SPX options. SPX options trade at the Chicago Board Options Exchange (CBOE) exclusively and are options on the actual S&P 500 Index. Because they’re options on the actual S&P 500 Index they’re very similar but not identical to SPY options. The SPX option bids and offers shown in Table 8.3 were noted at exactly the same moment as the SPY bids and offers used above.

Table 8.3 SPX Option Bids and Offers

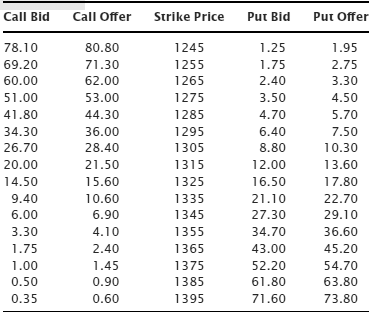
These options show much wider bid/ask spreads in dollar terms. This might make sense given the difference in cost of the underlying, but even the least expensive options like the 1395 calls and 1245 puts seem to have wide bid/ask spreads in dollar terms. What do they look like in implied volatility terms? (See Table 8.4.)

Table 8.4 SPX Option Bids and Offers by Implied Volatility

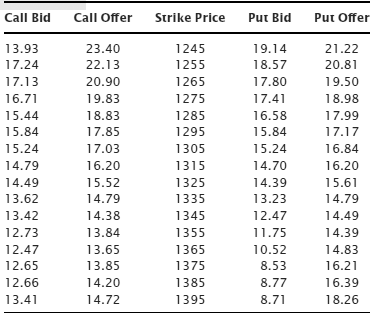
Wow, even in implied volatility terms these bid/ask spreads are really wide. The at-the-money call was the 1325 strike, and the spread between the bid and ask was 1.03 volatility points (15.52 – 14.49). Some of the deep-in-the-money bids are going to appear odd because SPX options are European-style meaning they can only be executed at expiration, but for the at-the-money call that shouldn’t have much impact on the width of the bid/ask spread.

What would a chart of the bid implied volatility and ask implied volatility for these calls look like? This is shown in Figure 8.3.

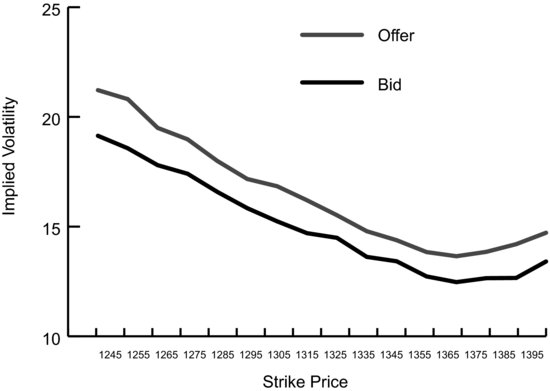
Comparing Figure 8.3 to Figure 8.1 shows a stark difference in the real bid/ask spread between SPY options and SPX options.

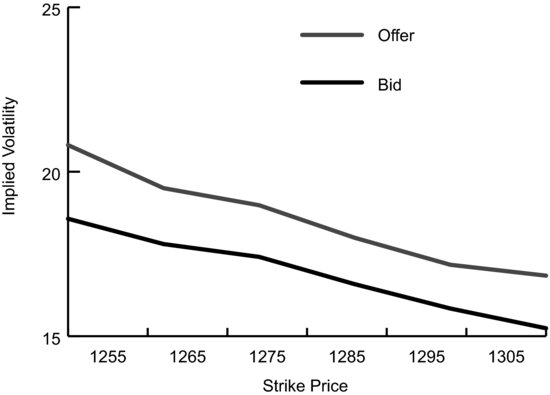
Let’s also look at a range of strike prices similar to the smaller range we looked at in Figure 8.2.

Comparing Figure 8.4 to Figure 8.2 also shows a startling difference in the real bid/ask spread between SPY options and SPX options.

THE BID/ASK SPREAD WHEN THERE’S MORE COMPETITION

These bid/ask spreads on a real basis, as measured by implied volatility, are huge, almost obscenely so. Why? Because SPX options are only listed on one exchange, the CBOE, so market makers in SPX options have no outside competition. They have much less reason to improve their markets by raising their bids and/or lowering their offers. This is likely to be the case for any option that is listed on only one exchange or that is thinly traded. In contrast, Russell 2000 options trade in much lower volume than SPX options, but the market for Russell 2000 options tends to be tighter in implied volatility terms because they’re listed on several exchanges and the universe of market makers has to compete for orders. It’s also likely that the actual bids and offers for SPX options are tighter than the electronic indication that we see. SPX options are still largely executed by traders standing face to face in a pit rather than electronically on a screen. If we were to call to the CBOE floor and ask for a quote it might very well be tighter than what we see on our screen. Or it might not.

The preliminary takeaway is that the real bid/ask spread, the spread in terms of implied volatility, is a function of many things, but one of those things is whether the options are multi-listed and how much competition there is between market makers. Since 2000, almost all equity options are multi-listed. Most ETF options (e.g. SPY) are multi-listed. Combine multi-listing with the huge interest in SPY options and you end up with very efficient option markets. There’s so much volume in SPY options that a market maker can make less per trade and make up for it with the greater volume. Since the SPX market makers have the market to themselves, they have no incentive to cut each other’s markets.

EQUITY OPTIONS

What if we do the same sort of option analysis for an equity, that is, for a single stock, rather than for an index or ETF? Do we find that the real bid/ask spread makes for relatively easy trading like SPY options or do we have to continue to really pay attention to our execution? Let’s look at options on Google (GOOG) in Table 8.5.

Table 8.5 Google Option Bids and Offers

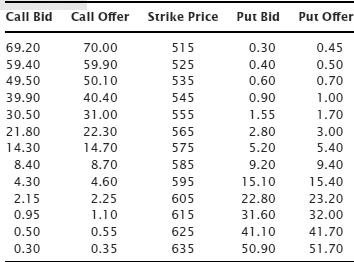
The widths of these bid/ask spreads seem moderately wide. They’re not huge like some SPX options, but they’re not $0.01 wide either.

By now we know that the real bid/ask spread is the one we get when we calculate implied volatilities. What are the implied volatilities of these prices for GOOG options? (See Table 8.6.)

Table 8.6 Google Option Bids and Offers by Implied Volatility

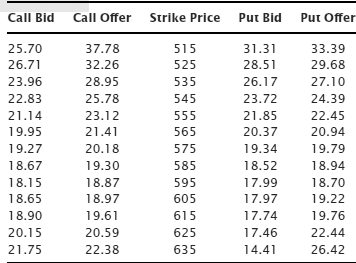
The real bid/ask spread, the one measured by implied volatility, is still pretty wide for Google options. The difference between the implied volatility for the 585 calls is 0.63 volatility points (19.30 – 18.67). The chart of these bids and offers by implied volatility can be seen in Figure 8.5.

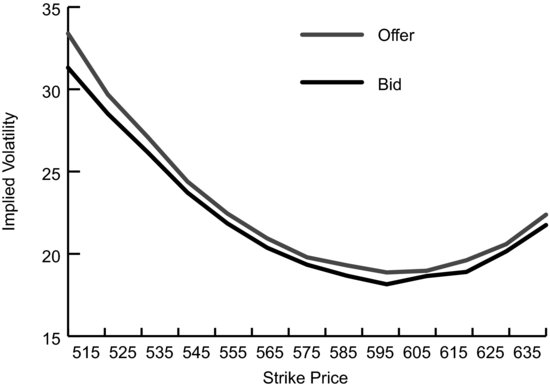
Google options are multi-listed, that is they’re listed on several exchanges, so why aren’t the real bids and offers tighter?

Multi-listing has almost certainly improved (i.e., narrowed) the width of the real bid/ask spread in GOOG options, so let’s look at the underlying stock. At the time these quotes were noted, the bid for GOOG stock was $584.04, and the ask for GOOG stock was $584.21. That bid/ask spread for Google shares is pretty wide all by itself. It’s much wider, even in percentage terms, than the $0.01-wide market we saw in SPY shares. If we compare that 585 call bid price of $8.40 to the stock bid price of $584.04 (remember that a market maker who buys calls is going to sell stock as a hedge), rather than the midpoint of the stock’s bid and ask as we did to calculate the implied volatilities we see in Table 8.6, we find that the implied volatility is 18.76. If we compare the call ask price of $8.70 to the stock ask price of $584.21 we find that the implied volatility was 19.23. In those terms the bid/ask for that call option is 18.76 bid versus 19.23 offered. The spread is only 0.47 in implied volatility terms. Consider the additional factor that only 200 shares of GOOG were bid for at $584.04, and that only 100 shares were offered for sale at $584.21. If, as hedgers, we have to execute 1,000 shares of GOOG, there’s also going to be slippage. If we’re buyers of the call we’re sellers of stock. We get to sell 200 shares at $584.04, unless someone beats us to them, and we’re going to have to sell 800 shares below $584.04, exactly where we don’t know, effectively increasing the implied volatility we’ve paid even further.

If we traders are sellers of the calls then we’re going to have to buy Google stock. We get to buy 100 shares at $584.21 but we’re going to have to pay more than $584.21 for the other 900 shares. We don’t know precisely what we’ll have to pay but it will effectively decrease the implied volatility of the option we’ve sold. All in all, the real market for GOOG options is pretty fair but we should probably still use limit orders to execute our trades someplace between these bids and offers for reasons we shall see.

THE BID/ASK FOR OPTION SPREADS

In a market with very small bid/ask spreads it’s easy to overlook the impact if you’re just buying or selling options outright. Giving up a half cent from fair value to pay the ask price on a SPY call isn’t likely to impact the outcome of our trade. The volatility-based spread may seem high, but the actual money at stake, literally $0.01, isn’t. But what about those trades that have several legs, such as butterflies? Now our trade has four different elements, and if we give up the width of the bid/ask spread four times (once for each wing and twice for the body since we do twice as many of those options) then it’s possible that we’re getting into territory where it’s tough to make money even if we’re right about volatility and direction. In options with wide bid/ask spreads it’s actually possible to get into a situation where it’s impossible to make money.

How do we calculate the bid and the offer for a spread from the markets in the constituent options? Let’s look at the SPY options again and look at a simple spread that’s buying one call option and selling another call option. If we wanted to buy the 135 call and sell the 136 call then what would the market, the bid and the offer, for that spread be?

The market is willing to sell the 135 call to us for $0.58. It’s simultaneously willing to buy the 136 call from us for $0.33. If we did both of those trades, bought the 135 call and sold the 136 call, we’d be long the 135/136 call spread and we would have paid $0.25 ($0.58 − $0.33) for the spread.

If we wanted to sell that same call spread we would have been able to sell the 135 call at $0.57. We would have been able to buy the 136 call at $0.34. If we did both of those trades we’d be short the 135/136 call spread and we would have received $0.23 ($0.57 − $0.34) for the spread.

From this it’s easy to see that the market is willing to pay $0.23 for that spread—that’s the bid for the spread. The market is willing to accept $0.25 for the spread—that’s the offer for the spread. The market for this spread is 0.23 bid/0.25 ask on legs.

Why is this spread, which would require very little hedging from the market maker, wider in terms of bid/ask spread than a much riskier outright option? Both of the constituent options have a bid/ask spread that’s only $0.01 wide. If we assume that fair value of these SPY options is the midpoint of the bid and the ask, then we have a fair value of $0.575 for the 135 call and of $0.335 for the 136 call. Using those values, what’s the fair value of our spread? It turns out that it’s $0.24. Market makers will go hungry if they buy and sell at fair value all day. The highest bid that provides some profit is $0.23; the lowest offer that provides some profit is $0.25. It’s no accident that those are the same bid and offer we got when we calculated the market by looking at the individual legs.

Market makers in very liquid options like options on SPY will calculate their idea of an option’s fair value to at least one decimal place. If a market maker thinks the 135 call is worth $0.5725 then he might well be willing to bid $0.57 and offer $0.58 simultaneously. What does this mean for our call spread? If the same market maker thinks the 136 call is actually worth 0.3375 then on legs he thinks the 135/136 call spread is worth $0.2350 ($0.5725 − $0.3375). In this case he might very well bid $0.23 for this spread and offer it at $0.24.

Google on the other hand has very wide markets. If we wanted to buy the 585/595 call spread in Google then we see that the market is willing to sell us the 585 call for $8.70 and willing to pay $4.30 for the 595 call. If we executed those trades we would have paid $4.40 ($8.70 − $4.30) for the spread.

What if we wanted to sell that same 585/595 call spread? The market is willing to pay us $8.40 for the 585 call and is willing to sell us the 595 call for 4.60. In this case we would have sold the spread for $3.80.

This market for the Google 585/595 call spread, 3.80 bid/4.40 ask, is the market for this spread on legs. This may very well be different from the bid/ask quoted if we asked for a market for the spread as a package, that is, as a single trade. The value of this spread is probably close to the difference in the midpoint for both options. If we do that math we find that the 585 call is probably worth close to $8.55. The 595 call is probably worth close to $4.45. Using those prices the spread is probably worth close to $4.10. There’s very little hedging a market maker would have to do if we executed our trade as a spread, that is, sold them one leg and simultaneously bought the other leg. The delta of the one leg would largely offset the delta of the other leg. The market maker on the opposite side of our spread would only have to hedge the difference. An option pricing model tells us the delta of the 585 call is 42. It also tells us the delta of the 595 call is 31. The delta of the 585/595 call spread is 11 (42 − 31). If a market maker bought one of these spreads he’d have to sell just 11 shares of GOOG.

If traders or market makers in GOOG options were lazy or obstinate or thought we were foolish enough to just sell this spread at $3.80 (the bid on legs) or buy it at 4.40 (the offer on legs) then they might not budge on their market of 3.80 bid/4.40 ask for the spread as a package. In that case it makes sense to “get in the middle.” If we want to buy this spread we could enter a limit order to pay $4.10 for the spread. This might prompt someone to offer the spread for sale at $4.20 (after all, it’s only worth the $4.10 we’re bidding). We’ve gotten them to improve their offer, which we can now buy.

If we wanted to sell the spread we could enter a limit order to sell at $4.10. This might prompt someone to bid to buy the spread at $4.00, a bid we could now sell.

This means we’d expect to pay/receive a price very close to the actual value of the spread. If we called our broker and asked for the market for the 585/595 call spread we’d probably get a quote around that $4.10 value. In this case the market for the spread was quoted at $4.00 bid, $4.20 offered.

THE BID/ASK OF MULTI-LEGGED SPREADS

Imagine we believe that Google is going to move sideways or down between now and expiration of these options. We decide we want to sell a call butterfly in Google to collect some premium and to profit if our outlook is correct. If we decide to sell the 585/590/595 butterfly we’re going to sell one of each of the 585 calls and the 595 calls and we’re going to buy two of the 590 calls. Our maximum potential profit is the net premium we receive and our maximum potential loss is $5 (the distance between any two strike prices) less the premium we receive.

If we execute all of these options at the market, that is, we sell at the bid price and buy at the ask price, then how do we make out? Let’s use the prices we used previously and see. We’d sell one of the 585 calls at $8.40 and we’d sell one of the 595 calls at $4.30. We’d take in a total of $12.70. We’d also buy two of the 590 calls at $6.40 each for a total of $12.80. We’ve spent $12.80 and we’ve taken in $12.70 so we’re actually selling the butterfly for a net debit of $0.10. And that’s our maximum profit! The very best we can hope for is a $0.10 loss. That means our maximum potential loss is $5.10. Because of the width of the bid/ask spread we’ve put on a trade that can never make a profit.

When trying to trade multi-leg spreads in names with wide bid/ask spreads your execution is absolutely vital to profitability. Brokers will take your order as a spread, meaning they’ll execute the trade as a butterfly rather than as a series of individual orders. Even then, using a limit order is critical.

What’s the fair value for our Google butterfly? If we could do all the legs at the midpoint of each respective bid/ask spread then we’d sell the 585 call at $8.55 and the 595 call at $4.45. That’s a total of $13.00 we would collect. We’d pay $6.25 for each of the two 590 calls to complete the butterfly, or a total of $12.50. This time we’ve received a net credit of $0.50 for selling our butterfly. That’s more like it.

WHAT’S THE REAL FAIR VALUE OF AN OPTION BASED ON THE BID/ASK?

It’s natural to look at a bid/ask spread and think that the real fair value for that option, as determined by the market, is the midpoint. That’s likely to be really close in certain options including those with narrow bid/ask spreads and those that are really liquid. However, this assumes that the next initiator of a trade is equally likely to be a seller as a buyer, meaning that our market maker feels that when selling an option the odds of buying it back soon are pretty good. If that’s so, then the bid/ask should be symmetrical around the fair value.

For options that are illiquid, the asymmetries of both pay off and information come into play. Market makers may feel that if they sell an illiquid option there’s no way of knowing if the next order is going to be a sell or a buy. They may feel that they’re at an information disadvantage and that they need to protect themselves from a catastrophic loss by leaning their bid and ask so that they’re a little more likely to be buyers than sellers. Thus, in the case of illiquid options, market makers will lean their bids and offers such that their bid is closer to their opinion of fair value, and their offer is further away. Since the potential damage from being wrong when selling an option is greater than the potential damage from being wrong when buying an option, and since it can be much more difficult to buy back options in a very thinly traded name and that this problem can become much more severe in the midst of turmoil, our market makers will lean a little toward being on the buying side. This will change if our market makers feel more confident or if they’ve accumulated a large position and need to lean their bids and offers differently in order to facilitate closing out this position.