Appendix
STANDARD DEVIATION
Standard deviation is a statistical measure of variability among a data set such as the daily percentage returns of an investment portfolio or equity index.
A low standard deviation indicates that the data points tend to be very close to the average of all the data points, while a high standard deviation indicates that the data points are spread out over a larger range from the average of all the data points.
As we’ve seen, standard deviation is often used to measure confidence in statistical results. We would be about 68 percent certain that any data point would be within 1 standard deviation of the average of all the data points. We’d be about 95 percent certain that the data point would be within 2 standard deviations of the average of all the data points.
The formula for standard deviation is:
![]()
Let’s calculate the standard deviation for some daily index returns by hand to better understand the concepts. In real life there’s no reason to do this as any spreadsheet can accomplish the calculation nearly instantaneously.
10 Days' Returns
0.56%
–0.22%
0.64%
0.45%
–0.81%
0.70%
–0.11%
1.01%
0.37%
–0.67%
Step 1: Calculate the average of all 10 data points.
![]()
Step 2: Calculate the deviation of each data point from the average and the square of that deviation.
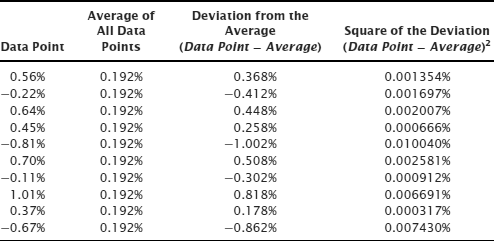
Step 3: Calculate the sum of all the squared deviations. The sum of the squares of the deviations is 0.033696 percent.
Step 4: Divide the sum of the squares of the deviations by n – 1.
![]()
Step 5: Find the square root of the solution in Step 4.
![]()
0.612 percent is the standard deviation of the daily returns for the 10 days we’re examining.
REALIZED VOLATILITY
Every trader and investor knows realized volatility when they see it; prices bounce around significantly and demonstrate big moves.
How can we calculate realized volatility so that it is objective and in units that we can compare to the implied volatility that we see in an option pricing model at OptionMath.com?
Realized volatility is the standard deviation of the natural log of daily returns multiplied by the square root of 260 (the approximate number of trading days in a calendar year).
The natural log is the logarithm to the base e, e being the constant approximately equal to 2.718281828. The natural log of a number x is the power to which e would have to be raised to equal x, it is commonly written as ln(x). The natural log is commonly used in finance, most often in calculating rate of return and the time for asset growth.
Let’s calculate the realized volatility of the 10 daily percentage changes we looked at in the discussion of standard deviation. To calculate the realized volatility, we need to start with the actual asset prices so that we can calculate the natural log daily returns. The natural log return for any day is:
![]()
| Closing Price | Percentage Daily Return | Natural Log Daily Returns |
| 100.000 | ||
| 100.560 | 0.56% | 0.0055844 |
| 100.339 | −0.22% | −0.0022024 |
| 100.981 | 0.64% | 0.0063796 |
| 101.435 | 0.45% | 0.0044899 |
| 100.614 | −0.81% | −0.0081330 |
| 101.318 | 0.70% | 0.0069756 |
| 101.207 | −0.11% | −0.0011006 |
| 102.229 | 1.01% | 0.0100493 |
| 102.607 | 0.37% | 0.0036932 |
| 101.920 | −0.67% | −0.0067225 |
The standard deviation of these natural log daily returns is 0.0061154. Thus, the realized volatility for these prices is:
![]()
VOLATILITY FOR DIFFERENT TIME PERIODS
The realized volatility we just calculated and the volatility input to any pricing model, including the implied volatility we might derive from observed prices, are expressed in terms of the expectations we have for change in the asset price. Since different assets have different absolute prices, the important measure of price change is the percentage price change.
By convention these volatilities apply to one calendar year so the volatility is the standard deviation of annual percentage price changes.
But what if we want to know what an annual volatility (standard deviation) of 20 percent says about the likely price change tomorrow or next month. How do you convert that volatility of 20 percent into a meaningful number for a shorter (or longer) time frame?
As we’ve already seen, standard deviation changes in proportion to the square root of time. So, volatility for a time frame other than a year is the annual volatility divided by the square root of the number of relevant time periods in a year.
How large a daily price change would we expect (with the 68.2 percent certainty we’d have given a range that’s 1 standard deviation up and 1 standard deviation down) if the annual volatility was 20 percent?
![]()
Any security displaying annual volatility of 20 percent would be expected 68.2 percent of the time to have a single day’s percentage return to fall between +1.24 percent and –1.24 percent.
What does this 20 percent annual volatility say about the 68.2 percent expectations for a monthly move?
![]()
Notice that the monthly move isn’t 20 times the daily move despite there being approximately 20 trading days in a calendar month. Again, that’s because changes in risk aren’t linear with respect to time. Rather risk changes with the square root of time.
THE BLACK-SCHOLES FORMULA EXTENDED, PUTS AND THE GREEKS
The Black-Scholes formula for the value of a call option is:
![]()
Where:
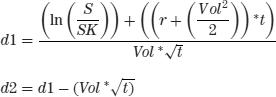
| And where: | S is the price of the underlying stock |
| SK is the strike price of the call option | |
| r is the annual risk-free interest rate | |
| Vol is the annualized standard deviation of underlying stock returns | |
| t is the time to expiration (in annual terms such that 6 months is 0.5) | |
| e is the base of the natural log and is equal to 2.7183 | |
| ln is the natural logarithm | |
| N represents the cumulative standard normal distribution. This cumulative distribution describes the probability of a random variable falling within a certain interval. The cumulative distribution value for any number can be found in online tables or can be calculated using a spreadsheet. |
The Black-Scholes formula for the value of a put option is:
![]()
Where:
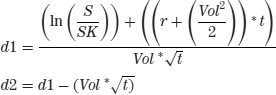
The Greeks—delta, gamma, vega, and theta—for a call option.
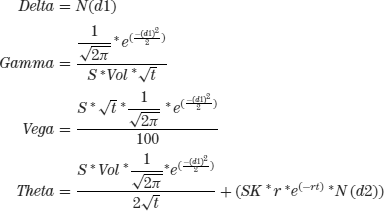
This theta formula is the generally accepted formula for theta but since time is measured in years in order to get a number that represents a single day’s erosion, which is both more common in actual usage and more useful, divide by 365.
The Greeks—delta, gamma, vega, and theta—for a put option.
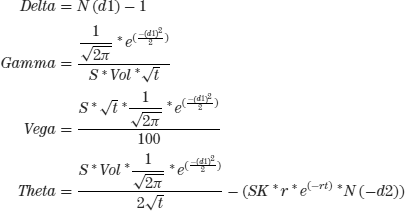
This theta formula is the generally accepted formula for theta but since time is measured in years in order to get a number that represents a single day’s erosion, which is both more common in actual usage and more useful, divide by 365.
It’s no accident that the formula for gamma and vega are the same for call options and put options.
Delta, gamma, vega, and theta aren’t the only Greeks that professional options traders pay attention to. As we’ve discussed there are others include rho, an option’s sensitivity to changes in interest rates, omega, a measure of the change in an option’s price with respect to the percentage change in the underlying price, and zomma, the change in the gamma of an option due to changes in volatility. The list goes on.
Some practitioners express theta as a negative number to represent the daily price change due to the passage of time. However, I’ve always looked at as the daily erosion of an option price. As such, and for these purposes, it’s a positive number.
LINEAR INTERPOLATION
Linear interpolation is a handy method of describing a value using adjacent data points. For example, if a stock was trading at 72.34 and you wanted to estimate what a call option with a strike price exactly equal to 72.34 would cost you could do so using the 70 and 75 strike options.
The formula for linear interpolation is:
![]()
In this example if the 70 strike call was trading at 3.60 and the 75 strike call was trading at 0.70 then we could approximate the value of a 72.34 strike call by:
![]()
ANNUALIZING YIELD
A quick way to annualize the yield from selling a covered call or the cost of buying a protective put—or for any other option strategy—is to simply multiply the yield by the number of relevant periods in one year. This generates an estimate, but the estimate doesn’t take compounding into account. If we want to be more precise and calculate an annualized number that takes compounding into account then we’ll end up with a result that is more consistent with other measures of investment performance.
The formula for annualized investment performance is:
![]()
| Where: | Yield is the period yield from selling the covered call (or period cost for buying a protective put) |
| N is the number of periods in a calendar year. |
For example, in Chapter 10 we discussed selling a 30-day to expiration covered call for $4.00 when the underlying was priced at $77.00. We calculated an estimate of the annual yield as 62.40 percent (4.00/77.00 * 12). A more precise calculation would generate an annualized yield of 83.7 percent:
![]()
The significant difference between the quick method and the more accurate method is a function of the period yield. If this period yield was lower the difference between the results generated by the two methods would be lower.
