CHAPTER 13

Risk Reversal

Just as calendar spreads isolate the benefit of differences in time decay, risk reversals isolate the phenomena of skew to the option trader’s advantage. With a risk reversal, option traders get to sell expensive options while buying cheap options, usually get to pocket some premium, and get long exposure to a stock they think is going to appreciate—all while generating a potentially significant margin of error in which the worst thing that happens is the risk reversal expires worthless and they keep any premium received. While it’s possible to establish a risk reversal at a debit, and we’ll discuss that later, it’s generally best for a risk reversal to generate a net credit, even if it’s small. Likewise, any net debit should be relatively small.

A risk reversal is constructed by selling a put option and buying a call option of the same expiration, but with a higher strike price. The premium received for selling the put option is generally greater than the premium paid in buying the call option. This difference is due to skew and results in the standard risk reversal generating a net credit to the option trader, even if the call is the same distance from at-the-money as the put. If the risk reversal were done for zero net premium, we would expect the call option bought to be closer to at-the-money than the put option sold.

The XYZ 95/105 risk reversal shown in Table 13.1 would consist of being long the XYZ 105 strike call option at a cost of $2.50 and short the XYZ 95 strike put option, generating $2.75. The net credit from doing the risk reversal would be $0.25 ($2.75 – $2.50).

Table 13.1 A Risk Reversal

	Price
XYZ Stock	100.00
Buy XYZ 30-Day 105 Strike Call	2.50
Sell XYZ 30-Day 95 Strike Put	2.75
Net Credit	0.25

A RISK REVERSAL AND SKEW

Skew is one of the phenomena discussed in Part Two. Due to several factors, including the flawed assumptions of option pricing models and the tendency for investors to insure their stock holdings via put purchases, options with strike prices below at-the-money (i.e., put options) generally display implied volatilities that are higher than the implied volatilities of options with strike prices that are above at-the-money, even if the put and call are equidistant from at-the-money. If the implied volatility for every strike price in an expiration cycle were plotted, it would show the curve that we’ve called skew. Figure 13.1 shows implied volatility plotted for SPY, the S&P 500 ETF, and how it is used to construct a risk reversal.

A risk reversal generates a long position in the underlying stock by selling the left side of the skew chart (which is the higher side in terms of implied volatility) in the form of a put and buying the right side of the skew chart (which is the lower side in terms of implied volatility) in the form of a call option.

A risk reversal is always a bullish strategy since both legs of the trade are bullish. (See Table 13.2.) Selling a put is mildly bullish and using that premium generated to buy a call option adds to the bullishness. The total bullishness of the position, expressed as the total delta of the two legs, depends on how far each is from at-the-money. The closer each leg is to at-the-money, assuming both legs are still out-of-the-money, the higher the total delta of the risk reversal and the greater the bullishness of the position.

Table 13.2 XYZ Risk Reversal Bullishness with Underlying at 102.50

Option	Delta
90 Strike Put	−12
95 Strike Put	−22
100 Strike Put	−40
105 Strike Call	38
110 Strike Call	20
115 Strike Call	8
Total Delta
90/115 Risk Reversal	20
95/110 Risk Reversal	42
100/105 Risk Reversal	78

Let’s say the underlying stock is below the put strike price at expiration; we, by using a risk reversal, are going to have the stock put to us and must pay the strike price of the put option. If the underlying stock is above the call strike price at expiration we’re going to choose to exercise the call option we’re long and will pay the call strike price for the stock.

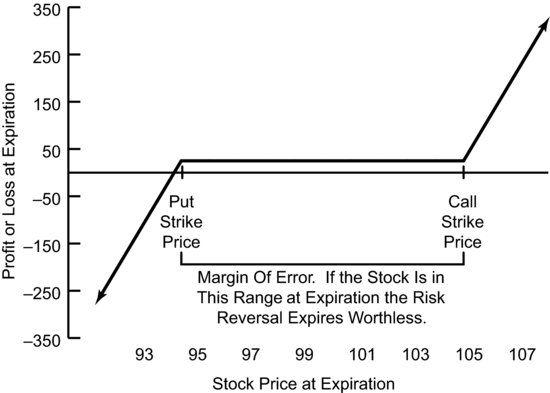
If the stock falls inside the range between the strike prices at expiration, above the put strike price and below the call strike price, then risk reversal users do not buy the stock. Both options will expire worthless and we will keep (lose) whatever net premium we received (paid) when executing the risk reversal.

What is the profitability of the XYZ 95/105 risk reversal we looked at previously? See Table 13.3, which shows that, if we bought the 105 call at $2.50 and financed it by selling the 95 put at $2.75, we’d generate a net credit of $0.25. Table 13.3 shows the profitability across a range of prices.

Table 13.3 Profit and Loss From the XYZ 95/105 Risk Reversal

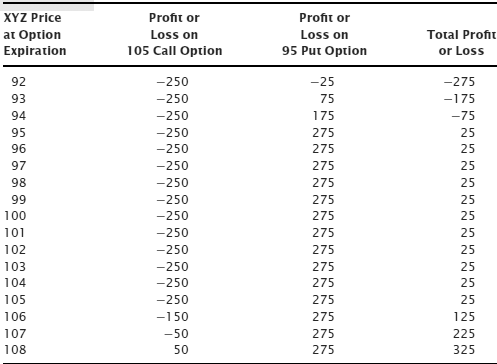
Figure 13.2 shows the payoff chart for this risk reversal including the area between the strike prices, which generates a small profit.

WHEN TO USE A RISK REVERSAL

Since a risk reversal is always a bullish strategy it is best used on underlying stocks that we are bullish on. If we were very bullish then we’d want to use another strategy, such as an outright purchase of the stock or the purchase of an at-the-money call option.

If we thought the underlying stock would likely head higher but might be stuck in neutral, then we’d sell a put option as we discussed in Chapter 11, but wouldn’t buy a call option. By simply selling a put, we make money if the stock goes nowhere but underperform if the stock rallies enough. By adding a long call option to the put sale, a trader adds significant upside to the trade if the stock rallies. A trader using a risk reversal should be more bullish than a put seller.

As with any strategy that involves selling a put option, a risk reversal should only be used on underlying stocks that a trader is willing to own. Since the net premium received for using a risk reversal is usually relatively small and might be slightly negative, the discount if the stock drops below the put strike price at expiration is also relatively small; in our XYZ example the discount would only be the $0.25 credit received. If the stock dropped below the put strike price the effective purchase price would be $94.75. If the risk reversal were initiated at a debit, the stock would be put to the trader at an effective price slightly above the put strike price. As such, a risk reversal isn’t a good way to buy a stock at a discount. Rather, it’s a good way to get long exposure to a stock while creating a margin of error in the form of a range between the strike prices where nothing happens. Inside that margin of error the entire trade expires worthless.

Since using a risk reversal results in being short a put option, your broker will require you to leave cash or margin availability in your account to pay for the stock if it’s put to you. While your broker will be satisfied with margin capability in your account, we won’t consider using margin, and all the payoff charts and profit and loss calculations will ignore the effects of margin.

USING A RISK REVERSAL

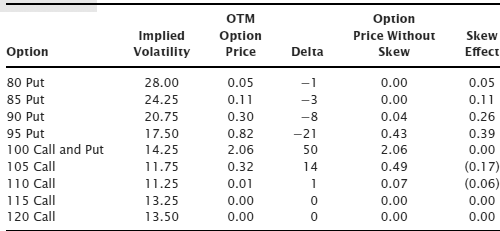
Since skew is most prevalent and obvious in equity index products let’s examine SPY for a risk reversal example, as seen in Table 13.4. SPY was at $140.71 when these prices were observed.

Table 13.4 Skew and Delta for a SPY Risk Reversal

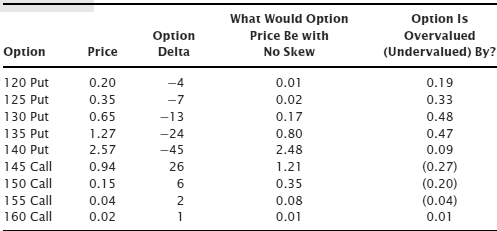
If we were simply interested in maximizing the positive impact of skew on option prices we would select the 130/145 risk reversal. We would sell the 130 put at $0.65, $0.48 more than it would be worth if it weren’t for skew, and we would use the proceeds to buy the 145 call at $0.94, about $0.27 less than the option would be worth if it weren’t for skew. Since the 145 call costs more than we will receive for selling the 130 put, we will have to pay $0.29 ($0.94 – $0.65) to execute this trade.

There is no downside breakeven for this trade because it cost money to put on. There’s no price to which the stock could break that would result in a profit on the option trade. That doesn’t mean it’s necessarily a bad trade, it just means the stock has to rally for a risk reversal executed at a net debit to be profitable. For this risk reversal the upside breakeven is $145.29. At that point, at expiration, the risk reversal will result in buying the shares at $145.00 and the gain will be equal to the $0.29 paid initially. Above that breakeven level at expiration the trade makes $1 for each $1 the underlying rallies; above this level it’s essentially a long position in the stock.

SPY was at $140.71 when these prices were observed. That means that the breakeven point ($145.29) required only a 3.25 percent increase in the price of the underlying stock. There is no downside breakeven but since the entire trade cost only $0.29 we can compare the rally required to get to breakeven to the drop that would result in having the stock put to us. That happens with SPY below $130 at expiration and would require a drop of 7.61 percent, as we see in Table 13.5. We could consider the $0.29 paid for the risk reversal as the price paid to have good things happen with only a 3.25 percent increase while keeping bad things from happening unless we experience a drop of 7.61 percent.

Table 13.5 SPY Risk Reversal

Buy 145 Call	0.94
Sell 130 Put	0.65
Net Premium Paid	0.29
Total Delta	39
Downside Breakeven Point	None
Upside Breakeven Point	145.29
Drop in Stock Required to Have Stock Put to Trader	7.61%
Rally Required to Achieve Upside Breakeven	3.25%

This trade highlights the danger of being locked into the idea that a risk reversal (or its opposite trade, a collar) needs to be done at no cost or for a credit. Sometimes, the expenditure of a little bit of premium will result in strike prices and a payoff chart that are superior to those generated from a risk reversal that is done at a credit. Figure 13.3 shows the payoff chart for this risk reversal.

How much long exposure does this risk reversal generate? The delta of the put sold is –13 and the delta of the call option bought is 26. The total delta is 39 (the impact of selling a put which has negative delta is to gain positive exposure or positive delta).

This total delta of 39 doesn’t really give us much exposure in the case of a small movement. Remember from Part One that a delta of 39 means that if SPY rallies by $1 we’d expect our risk reversal to increase in value by $0.39. As SPY rallied this delta would gradually increase, and since the 145 call is the lowest call strike price that is out-of-the-money among those strike prices we looked at, our trader may be very happy to use this combination of strike prices.

However, our trader may want more exposure meaning he wants a higher total delta. Is there another risk reversal that would generate a net credit as well as a higher delta? The 135/145 risk reversal offers almost as much positive effect of skew and offers much more market exposure since the delta is higher. In executing the 135/145 risk reversal our trader would sell the 135 put at $1.27, $0.47 more than the option would be worth if it weren’t for skew, and would use part of the proceeds to buy the 145 call at $0.94. The result is a net credit of $0.33.

This risk reversal offers more exposure to price changes in the underlying stock because the put option sold is closer to at-the-money. The delta of the 135 put was –24, meaning the delta of the second risk reversal was 50 (selling the 135 put generates positive delta of 24 while buying the 145 call generates positive delta of 26) as you can see in Table 13.6. Over short distances, this risk reversal will change in price by about half of the change in SPY. Our trader has accomplished the goal of getting more exposure to changes in the price of SPY and has also put the risk reversal on for a net credit.

Table 13.6 New SPY Risk Reversal

Buy 145 Call	0.94
Sell 135 Put	1.27
Net Premium Received	0.33
Total Delta	50
Downside Breakeven Point	134.67
Upside Breakeven Point	None
Drop in Stock Required to Achieve Downside Breakeven	4.29%
Rally Required to Achieve Call Strike Price	3.05%

The downside breakeven for this trade, the 135/145 risk reversal, is $134.67. This trade has a downside breakeven because it was done at a net credit; there is no upside breakeven. If the stock were to rally it would simply add to profits. Figure 13.4 shows the payoff chart for this risk reversal.

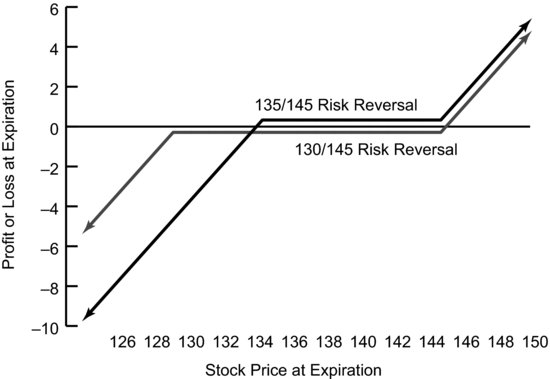
This second risk reversal, the 135/145, was executed for a credit. At what cost? First, since it has a higher delta it has increased exposure to changes in the price of SPY. That might be good or bad. If SPY falls in price, then the value of the 135/145 risk reversal will fall faster than will the value of the 130/145 risk reversal. Second, exposure on the downside will happen sooner because the strike price of the put is now higher. If the SPY were at 130 at option expiration, the first risk reversal (the 130/145) would expire worthless and the net outcome would be the loss of the $0.29 initially paid. However, if SPY dropped to 130, the second risk reversal (the 135/145) would result in a loss because the 135 is now in-the-money. The loss from this second risk reversal would be $4.67, a $5.00 loss on the 135 put our trader is short less the $0.33 credit received at initiation. Figure 13.5 compares the payoff charts for both risk reversals.

RISK REVERSALS PRIOR TO EXPIRATION

The delta effect we’ve discussed results in market exposure from the time we put the trade on. Since the delta for a risk reversal can be fairly large, often representing 50 percent or more of the move in the underlying stock, a risk reversal can be a proxy for a long position in the stock in a way that other option strategies can’t. Simply selling a put option, as we discussed in Chapter 11, doesn’t generate a delta of 50 or greater unless the put option sold is at-the-money or in-the-money. A calendar spread can be bullish but it can go too far and become bearish. Covered calls and short puts need less movement, not more.

This delta effect means that a risk reversal doesn’t require the stock to rally above the call strike price in order to be profitable. Rather the risk reversal will increase in value as the underlying stock rallies even if it doesn’t get above the call strike price. While an outright long call will increase in value as the underlying rallies, an outright call is always fighting erosion. For a risk reversal the negative effect of erosion on the call option is balanced by the positive effect of erosion on the put option. However, eventually time decay becomes a problem as the long call option begins to erode more quickly once it’s at-the-money.

There are several good ways to mitigate the impact of erosion if the underlying rallies and the call becomes at-the-money. We’ll explain these later when we discuss follow-up action.

It’s impossible to know what a risk reversal will be worth given a specific price for the underlying until expiration, but if we make some assumptions about skew (always a very dangerous thing) it is possible to approximate what a risk reversal would be worth before expiration. This exercise, as shown in Table 13.7, is done only so that readers can see a possible outcome prior to expiration. It requires assumptions about skew, implied volatility, the passage of time, and how all of those interact. The example assumes an at-the-money price of $100.00, the at-the-money implied volatility was 14.25 percent, and there were 50 days to expiration.

Table 13.7 Risk Reversal Alternatives

There are several risk reversals we could select from among these options. If we wanted to maximize the positive effect of skew on option prices and simultaneously get the maximum delta exposure while using out-of-the-money options, we would execute the 95/105 risk reversal for a $0.50 credit. We would do this by selling the 95 strike put at $0.82 and buying the 105 strike call for $0.32. Due to skew the 95 put is “overpriced” by $0.39 and the 105 call is “underpriced” by $0.17; the risk reversal is worth $0.56 more than it would be if there were no skew. The delta of this 95/105 risk reversal is 35 (selling the put with a negative delta of 21 and buying the call with a positive delta of 14 generates a positive delta of 35).

It is not always possible to simultaneously maximize the skew effect and delta, as we’ve seen in the SPY example in Table 13.4.

What would this 95/105 risk reversal be worth if just after initiation the underlying moved to 105? Using an option pricing model like the one available at OptionMath.com it’s possible to estimate. In that case, using the same relative implied volatilities the risk reversal would look like the one in Table 13.8.

Table 13.8 The 95/105 Risk Reversal After a Rally to 105

The total unrealized profit from the risk reversal is $2.26 ($0.52+ $1.74). Observant readers will notice this is more than would be expected from a 5 point move for a 35 delta option position. This is due to the fact that delta changes as the underlying moves. The originally observed delta of 35 is only valid over short distances. As the underlying rallies this delta increases (this is the effect of gamma). With the underlying at 105 the delta of this risk reversal would be 59.

What would the risk reversal be worth if the underlying had not moved but time had passed? What would the risk reversal be worth with 25 days to expiration with the underlying at $100.00? We see this scenario in Table 13.9.

Table 13.9 The 95/105 Risk Reversal After the Passage of Time

In this situation the risk reversal has made $0.26 ($0.50 – $0.24) even though the risk reversal is bullish and the underlying hasn’t moved. The only thing that has changed is that time has passed. You’d expect a risk reversal executed for a credit and with the strike prices equidistant from at-the-money to be profitable in this situation.

These examples are offered only with the caveat that we’ve tried to isolate a single variable so that we can see its impact on a risk reversal. The markets rarely act like this. Obviously markets tend to move, implied volatilities tend to change, and the shape of the skew curve evolves.

These examples show that a risk reversal doesn’t require the underlying stock to be above the call strike price to be profitable, and the reason is the effect delta has on the risk reversal and the difference in the impact of time on the two options.

The value of the risk reversal will increase as the stock appreciates although eventually time decay becomes a problem. With the stock at the call strike price at expiration the worst thing has happened: You’ve been right but you’ve only made a tiny bit of money; you’ve made the amount of the credit the risk reversal generated, meaning that if you put the risk reversal on for a debit the whole thing ends up being a loser. This doesn’t mean you should only initiate a risk reversal for a credit, it just means you should have a good reason for paying to put one on.

A risk reversal is optimal, meaning the relationship between how far the strikes are out-of-the-money and the net credit received or net debit paid is most advantageous, when the general investing public hates a particular stock and has bid up the price of put options and has sold down the price of call options.

WHEN A RISK REVERSAL DOESN’T WORK

Risk reversals work because of put skew, meaning they work because implied volatility and the subsequent price of put options is higher than for call options. If there were no skew, the call would cost as much as the put and the risk reversal user would have no advantage. What about those underlying assets or stocks we discussed in Chapter 6, the ones that don’t exhibit put skew but rather exhibit call skew, meaning that calls are relatively more expensive than puts? Those assets included gold, crude oil, and some of the companies that produce these commodities, as well as companies that are seen as takeover candidates.

One example is GLD, the ETF that tracks gold prices. Table 13.10 draws on some recently observed prices for options on GLD.

Table 13.10 GLD Option Prices

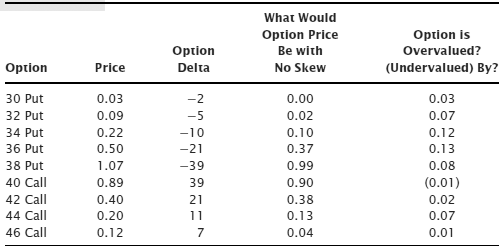
In our first example, the SPY example, any combination of short put and long call would have demonstrated an advantage generated by skew. In GLD that’s not the case. The 32/44 risk reversal would result in selling the 32 put for $0.07 more than it would be worth without skew and buying the 44 call for $0.07 more than it would be worth without skew. There’s no advantage there. That’s because gold tends to show either call skew or equal skew, which is what we see here. What about a stock that’s a takeover candidate?

One recent example of a stock that’s considered a takeover candidate is Yahoo! (YHOO). It, like many takeover candidates, shows call skew. What would a risk reversal in Yahoo! look like? First let’s look at some of the options available to construct our risk reversal in Table 13.11.

Table 13.11 YHOO Option Prices

In this situation the risk reversals we might pick all result in losing money to skew. Of the put options, the 13 put has the most additional value due to skew, so that might be the one we’d sell. However, every call is higher than it would be if not for skew, and each one is higher by more than that $0.03. The 13/16 risk reversal would result in paying $0.03 to put it on, and the net effect of skew would always be negative for this trade since the call bought is “overpriced” by more than the put sold. The 14/15 risk reversal would cost $0.05 to put on. Again, the net effect of skew would be negative.

In situations like this where call skew exists, it’s best to think of a risk reversal as a way to get upside exposure for a very low cost, although the requirement to deposit margin should be taken into account. The benefit of a risk reversal in a situation like this is that if the stock is between the two strike prices at expiration, we don’t have to worry about holding stock that isn’t rallying as we expected. However, if an offer had been made to buy the company, then it would likely be for a price greater than the strike price of the call we’re long. It shouldn’t be forgotten that bad news could still come out leaving us short a put and ultimately long the stock when we don’t want to own it. In a situation where call skew cancels out or overwhelms the benefit generated by put skew, there’s no reason not to use a risk reversal if we recognize that what we expect to go up might go down. There’s just no extra benefit generated by skew.

In the presence of put skew a risk reversal should usually be put on for a small credit, but if spending a small amount of premium generates a risk reversal with better risk/reward characteristics, we should spend the little bit of extra money. This is also the case with underlying stocks exhibiting call skew. This is true particularly if the result of spending a little in premium is that we participate at a price that is an important technical level on the stock chart.

RISK REVERSALS AND LONGER-DATED EXPIRATIONS

Risk reversals are usually hurt by extending the expiration. This is because option pricing assumes the underlying is going to appreciate by the risk-free rate of interest resulting in the at-the-money strike for a call option being above the current price for the stock. This is also why a stock at $100.00 will often have 100 strike call options with deltas greater than 50.

The result is that what we might think of as the at-the-money call is really in-the-money if the expiration is distant enough and a slightly out-of-the-money call might actually be at-the-money. Since the call is at-the-money, it will be more expensive. Similarly, the put option will be further out-of-the-money than we really believe it is and will have less value. This all means our option trader will collect less for selling the put option and must pay more to buy the call option. The normal economics of a risk reversal are changed by the more distant expiration. Table 13.12 shows deltas for hypothetical options at 30 percent implied volatility, 100 strike price, and the underlying at $100.00.

Table 13.12 Risk Reversals and Time to Expiration

Time To Expiration	Delta
Calls
1	50.7
5	51.5
15	52.6
30	53.6
90	56.3
180	58.9
360	62.4
Puts
1	49.3
5	48.5
15	47.4
30	46.4
90	43.7
180	41.1
360	37.6

In some cases the call strike price can be significantly above the current price. This happens if interest rates are high and the options are particularly long-dated. What strike price, assuming $1 wide strike prices, would have a call (and put) delta closest to 50 for these expirations in Table 13.12? Table 13.13 shows the at-the-money strike price increases for calls as the number of days to expiration increases.

Table 13.13 Time to Expiration and Moneyness

Time To Expiration	At-the-Money Strike Price
Calls
1	100
5	100
15	100
30	101
90	102
180	105
360	110

Time to Expiration and Risk Reversal Deltas

Let’s look at some different hypothetical options and the potential risk reversals in Table 13.14. Note that because these are hypothetical there is no skew in order to isolate the impact of time to expiration.

Table 13.14 Risk Reversal Time and Delta

Time to Expiration	Price	Delta
105 Call Option
15 Days	0.75	22
30 Days	1.57	30
180 Days	6.33	45
360 Days	9.80	49
95 Put Option
15 Days	0.66	−19
30 Days	1.42	−26
180 Days	5.93	−36
360 Days	9.21	−37
95/105 Risk Reversals
15 Days	0.09 Debit	41
30 Days	0.15 Debit	56
180 Days	0.40 Debit	81
360 Days	0.59 Debit	86

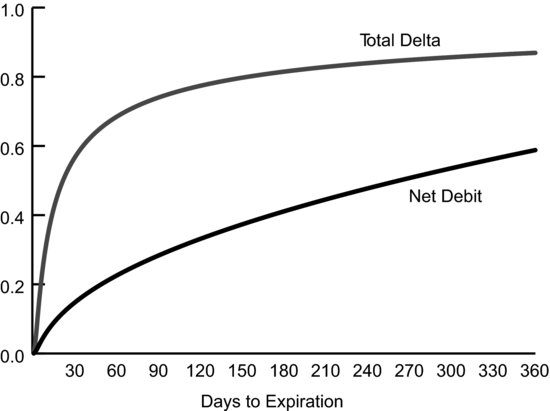
As time to expiration increases the call option gets more expensive relative to the put option. Thus, the risk reversal gets more expensive.

We also see that the delta of the risk reversal increases as time to expiration increases. This makes sense as the delta of each option increases as time to expiration increases. This is due to the idea that with more time to expiration; there’s a greater possibility for a call option that is currently out-of-the-money to become in-the-money at expiration.

Figure 13.6 shows how this hypothetical cost and delta changes as time changes. Changes in the price of the risk reversal are fairly linear, but the real impact is on the delta. As time to expiration increases the delta initially increases very rapidly and eventually levels off. If your major goal is to get delta exposure rather than use the option math of skew, then you’re better off using slightly longer dated options.

FOLLOW-UP ACTION

Follow-up action for a risk reversal isn’t as involved as it is for some of the other strategies we’ve discussed. In selling a put a trader may be most focused on collecting and keeping the premium received. This might result in rolling the position to keep from owning the stock. In a risk reversal the potential to get put the stock if it’s below the strike price of the short put might result in our trader wanting to close the put or roll down or down and out.

Since the initial trade probably didn’t generate much net premium, it’s much tougher to roll the put and not have the trade end up a big loser. In this case rolling the put down and out (so that the net premium paid for the follow-up trade is very small) is likely the best idea. The problem is that by rolling down and out we have extended the period during which we’re short a put option. If we think the issues that are weighing on the stock are transient then this may make sense, but we executed the trade in order to get long exposure to the underlying stock. We’ve been wrong. Rolling down and out will lower the strike price we’re short but it may not be low enough. We should recognize that by using a risk reversal we likely had the option math working for us and, thanks to the delta being less than 100, probably lost less money than we would have if we’d simply bought the stock.

If the stock is below the put strike price, then it’s probably best to recognize the trade for the loser it is and move on by closing the position and taking the loss. If the call option is worthless, or nearly so, there’s no reason to sell it. This is much like the situation we discussed previously. We could leave a good-till-canceled (GTC) order to sell the call at a reasonable price, something like $0.50. If the short put still has substantial time value remaining then it may make sense to leave the trade as it is. We expected the underlying stock to rally, so it may be near a bottom.

If the stock isn’t yet below the put strike price and there’s very little time to expiration it probably makes sense to simply monitor the trade in the hope that the stock stays above the put strike price and stays within the margin of safety between the two strike prices.

Since a risk reversal generates so little premium, and might actually be executed at a debit, the goal needs to be long exposure to the underlying stock. That doesn’t mean that we shouldn’t take advantage of the opportunity to make a better, more informed trade, particularly if the stock has rallied to our call option strike price so that erosion is now working against our position.

For example, Table 13.15 shows QQQ, the ETF that tracks the NASDAQ 100 index, at $66.25 with about 30 days to expiration.

Table 13.15 QQQ Risk Reversal

This is about what we would expect for a risk reversal, particularly one on an equity index. There’s significant put skew, as you can see from the fact that the put option is further from at-the-money ($66.25) than the call option but is still more expensive than the call. Since both options share an expiration, the expected daily erosion for the put option is greater since it’s more expensive, however the net expected erosion is tiny. This trade clearly has the option math working for it, but what would happen if QQQ rallied, as expected, and was at $68.00? How would this effect the risk reversal? Would the option math still be working in our favor? While it’s always difficult to assume what the trade would look like, Table 13.16 shows a reasonable estimate of what this trade would look like with QQQ at $68.00 and 10 days to expiration.

Table 13.16 QQQ Risk Reversal After a Rally

The risk reversal shows a profit of $0.90 ($0.78 value now plus the $0.12 already collected) as we’d expect given that QQQ has rallied. What about the rest of the term of the trade? Is the option math still working in our favor? Daily erosion is now working against us; the value of the risk reversal will erode by nearly $0.03 today, and as expiration approaches that erosion penalty will increase. If QQQ doesn’t move any further, the 68 strike call will expire worthless and the additional unrealized value of $0.78 will disappear. The entire profit will fall back to the $0.12 credit received for initiating the trade. Clearly, the passage of time and the option math are no longer working for this risk reversal, they’re now working against it. So what’s the right follow-up trade?

With 10 days left to expiration our trader needs to focus on the call side of this trade. It’s certainly possible that QQQ could fall below the 64 level before expiration, and many traders would buy back that nearly worthless put or would bid $0.05 for it. Either makes sense, although that would eat into the credit of $0.12. Buying back the put would also free up all of the cash or margin that’s currently being used. However, the call option is where the action is.

Our trader really has three alternatives: Leave the trade as it is, close the trade and take the profit, or roll the call.

Leave the Trade As It Is

Not every trade can always have the option math working in its favor and presumably our trader was bullish QQQ and put this risk reversal on for that reason. Right so far: There’s no reason to think that the rally is going to stop simply because QQQ has reached the call strike price. From this point forward the risk reversal will increase in value by $1 for each $1 rally in the price of QQQ, although that $1 increase in value will require holding the trade until expiration. As long as traders in this situation recognize that QQQ has to reach $68.78 at expiration to be as well off as they are right now, they should leave the trade on if they think that is likely.

Close the Trade

If traders think QQQ going substantially higher is unlikely, they may very well choose to exit the trade and take the profit. In doing so they would sell the call at $0.85 and buy back the put at $0.07. Traders shouldn’t get in the habit of taking off the call and staying short the teenie put option. Staying short this put option will usually work out since it will usually expire worthless but occasionally some unexpected news will come out and torpedo the stock or ETF, QQQ in this case, and the $0.07 they’re hoping to collect will end up being pretty expensive.

Roll the Call

The final alternative is to roll this long call. Simply rolling the call up will generate net premium since the 68 call sold will be more expensive than the upside call bought. This will add additional premium to the $0.12 received when the trade was initiated, but at the cost of reduced exposure to a continued rally because the delta of the new call will be lower than the delta of the 68 call. Since the new call option will be cheaper than the 68 call, the net daily erosion paid will be reduced as well.

Rolling the call up and out will reduce the net premium received for selling the 68 call to the point that no net premium might be received. However, since the new call option is both longer-dated and has a higher strike price, the penalty of daily erosion will be reduced, as we discussed in Part Two.