This chapter marks a departure in the book’s progression. Instead of describing the Cell’s capabilities as a processing device, the goal of this and succeeding chapters is to show how these capabilities accomplish practical tasks. This chapter concentrates on performing vector and matrix operations with the Cell, and it covers five topics:
The first topic is the Vector library (libvector). This provides functions for basic vector operations, such as the cross product and dot product. These functions run on the SPU and PPU and were designed primarily for engineers and graphics developers.
The Matrix library (libmatrix) contains routines that operate solely on 4x4 floating-point matrices. These run on the PPU and SPU, and are well-suited for manipulating pixels in graphics. These operations are also useful for performing scientific calculations in three-dimensional space.
The functions in the Large Matrix library (liblarge_matrix) manipulate square and nonsquare matrices of variable size. This library is available only for the SPU and is geared toward solving linear equations. Its functions perform such tasks as matrix decomposition, transposition, row/column swapping, and matrix solving.
The BLAS library (libblas) provides routines from the commonly used Basic Linear Algebra Subprograms standard. This library provides routines for vector-vector, matrix-vector, and matrix-matrix operations. All the BLAS functions are available for the PPU, and a subset of them can be run on the SPU.
The last topic in this chapter isn’t a library at all, but concerns one of the SDK’s sample projects: matrix_mul. This complex example takes maximum advantage of the Cell’s architecture to multiply two very large matrices. Matrix multiplication isn’t hard to grasp, but IBM uses many important techniques to optimize this application. The better you understand how this example works, the better you’ll be able to apply these techniques in your own code.
Before I describe the Vector library, I need to make an important distinction. So far, the term vector has been used as a synonym for SIMD (Single Instruction, Multiple Data), and has referred to processing multiple scalars at once or data structures that contain multiple scalars. But the Vector library is concerned with the vectors used by physicists, engineers, and graphics/game developers. These mathematical structures represent motion in space, physical forces, combinations of color components, and so on. As I learned it in school, a vector is simply a mathematical abstraction with a magnitude and direction.
Still, the Vector library functions operate on SPU vectors, specifically vector floats and pointers to vector floats. These functions are contained within libvector.a, which is available for the PPU (/opt/cell/sdk/src/lib/vector/ppu) and the SPU (/opt/cell/sdk/src/lib/vector/spu). The functions are declared in libvector.h, located in /opt/cell/sdk/src/lib/vector.
This presentation splits the libvector routines into two parts: functions that deal with vector products and lengths, and functions that perform graphic and miscellaneous operations.
Table 16.1 lists the traditional operations associated with vectors. These include the dot product, the cross product, and finding the length (norm) of a vector. Many of the functions have variants that end with _v. These operate on multiple vectors simultaneously.
Table 16.1. Vector Library Functions for Vector Products and Lengths
Function Name | Purpose |
|---|---|
| Take the dot product of two vectors |
| Calculate four dot products of three- and four-component vectors |
| Take the cross product of two vectors |
| Calculate four cross products of three-component vectors |
| Returns the length of |
| Returns four vector lengths at once |
| Returns the inverse of the length of |
| Returns the inverses of four vector lengths at once |
| Return a vector with the direction of vec and unit length |
| Normalize four vectors at once |
The first entries in the table perform the two most common vector operations: the dot product and cross product. The first returns a scalar representing how close vectors are and the second returns a vector whose magnitude is proportional to how divergent they are. If a = (ax, ay, az), b = (bx, by, bz), and θ is the angle between them, the following relationships hold:
a·b = axbx + ayby + azbz = |a||b|cosθ
a×b = (aybz − azby)i − (axbz − azbx)j + (axby − aybx)k = (|a||b|sinθ)n
The vector n is perpendicular to the plane containing a and b, and (i, j, k) are unit vectors pointing in the positive x, y, and z directions.
The dot_product3 and dot_product4 functions are straightforward. Each accepts two vector floats as input and returns a float result. dot_product3 uses only the first three components of both vectors and dot_product4 operates all four.
When you need to perform multiple dot products on values with three dimensions, dot_product3 isn’t very efficient. It only uses ¾ of each vector and adds elements within a vector, which takes more time than adding elements across separate vectors. For this reason, the Vector library provides dot_product3_v, which performs four efficient dot products at once.
Note
Most functions ending with _v require that their inputs be converted from AOS form to SOA before processing. This is called swizzling, and the process is explained in Chapter 8 for the PPU and Chapter 11 for the SPU.
To understand how dot_product3_v works, you need to recall the SOA versus AOS discussion in Chapters 8, “SIMD Programming on the PPU, Part 1: Vector Libraries and Functions,” and 11, “SIMD Programming on the SPU.” The AOS (array of structures) method stores different types of values in a vector, such as the (x, y, z) components of a point in space. The SOA (structure of arrays) arrangement stores similar scalars in vectors, so one vector may contain all x-components while another stores all y-components. The dot_product3_v function operates on SOA data, which means it uses every element of each input and performs addition across vectors rather than inside vectors.
In the dot product/cross product equations, |a| is used to represent the magnitude, or length, of the vector a. If vector a has components (ax, ay, az), its length is given by
The length_vec3 function computes the length of a single vector, and length_vec3_v computes the lengths of multiple vectors. There are no functions available for calculating the length of vectors with four components.
The reciprocal of the length can be obtained by calling inv_length_vec3 and inv_length_vec3_v. If a vector’s components are divided by its length, the result is called a normalized vector, which has the same direction as the original but length equal to one. This operation is performed by normalize3 and normalize3_v.
The functions in Table 16.2 perform a wide range of vector operations, from interpolation to vector creation. A number of them are particularly well-suited for building 3D graphic applications.
Table 16.2. Graphic and Miscellaneous Vector Functions
Function Name | Purpose |
|---|---|
sum_across_float3/ sum_across_float4 | Return sum of scalars within vector float |
| Create a vector float from four scalars |
| Create a vector signed |
reflect_vec3/ reflect_vec3_v | Reflect vectors across normal |
lerp_vec4/ lerp_vec2_v/ lerp_vec3_v/ lerp_vec4_v | Perform linear interpolation between vectors |
| Returns vector passing between two points on a plane |
| Returns a clip code for a vertex or vertices |
intersect_ray_triangle/ intersect_ray_triangle_v/ intersect_ray1_triangle8_v/ intersect_ray8_triangle1_v | Determine distance between rays and triangles |
xform_vec3/ xform_vec4/ xform_vec3_v/ xform_vec4_v | Transform a column vector by a matrix |
| Transform a normal vector |
The first function, sum_across_float, operates just as its name implies: It adds the three/four floats inside a vector and returns the result. Similarly, load_vec_float4 creates a vector float from four floats, and load_vec_int4 creates a vector signed int from four ints.
reflect_vec3 is the first of the libvector functions that will interest graphic developers. When light bounces off a surface, its vector must be reflected across the vector perpendicular to the surface—the surface normal. reflect_vec3 accepts a vector and a normal vector, and returns the reflected vector. reflect_vec3_v returns four reflected vectors.
In many cases, you might not know the exact components of a vector, but you know how close it should be relative to two other vectors. The lerp_vec functions perform linear interpolation, and they use a t parameter to identify where the vector should be placed. For example, if v1 and v2 are the vectors that bound the interpolation, the equation that generates the vector result vout is given as
vout = (1 − t)v1 + tv2
The Large Matrix library provides a similar function for spherical interpolation called slerp.
clip_ray is similar to lerp_vec, but the interpolation factor t is the output rather than an input. If vec passes through v1 and v2 and a specified plane, clip_ray returns the value of t such that the interpolated vector intersects the plane.
The OpenGL graphics library converts coordinates to normalized device coordinates (NDCs) before displaying them on the screen. These NDCs lie between −1 and 1 in the (x, y, z) directions, and vertices lying outside this range are clipped. clipcode_ndc returns a constant depending on where a vertex was clipped: CLIP_CODE_LEFT, CLIP_CODE_RIGHT, CLIP_CODE_BOTTOM, CLIP_CODE_TOP, CLIP_CODE_NEAR, and CLIP_CODE_FAR.
Instead of checking for intersecting planes, intersect_ray_triangle checks to see whether a ray intersects a triangle. If so, it returns the distance from the ray’s origin to the intersection and the location of the intersection, using the triangle’s parameterized coordinates. intersect_ray1_triangle8_v determines whether a ray intersects one of eight triangles, and intersect_ray8_triangle1_v determines whether one of eight rays intersects a triangle.
The last two functions in Table 16.2 perform vector multiplication. The xform_vec functions treat input vectors as column vectors and premultiply them by 4x4 matrices. This is commonly used in 3D graphics to transform vertices and colors. But transforming normal vectors is more complicated: You have to compute the transpose of the inverse of the matrix associated with regular vectors. xform_norm3 transforms a single normal vector, and xform_norm3_v transforms four normal vectors simultaneously.
The next section explains how 4x4 matrices are accessed and operated upon by the SDK. The example application shows how xform_vec3 is used in code.
The Matrix library (libmatrix) can be found in the /opt/cell/sdk/src/lib/matrix directory. There you’ll find a set of header files and folders for the ppu, ppu-shared, and spu versions of the code. This discussion focuses on the code in the spu directory, which contains source files, object files, and a single library: libmatrix.a.
Each function in the library operates on a 4x4 matrix of floating-point values. Most of the functions accept pointers to four vector floats, but one function accepts a pointer to eight vector doubles. Figure 16.1 shows how the elements are accessed in memory.
If a matrix is composed of vector floats, each row occupies a vector. If a matrix composed of vector doubles, each row takes up two vectors.
The libmatrix functions can be divided into three categories:
Basic matrix operations
Perspective matrix operations
Vector rotation
Functions in the first category are general-purpose routines that you can find in any matrix library. But the functions in the second and third categories are more specifically geared toward 3D graphic development.
Table 16.3 lists the common functions available for operating on 4x4 matrices. Each returns void and most only accept pointers to vector floats (vf*) as arguments. Some accept pointers to vector doubles (vd*).
Table 16.3. Basic Functions in the Matrix Library
Function Name | Purpose |
|---|---|
| Initialize |
| Set |
| Set |
| Multiply elements of |
| Set |
| Convert vector float to vector double |
| Convert vector double to vector float |
| Replicates each element of in into a separate vector float |
The first three are the simplest, and are comprehensible to anyone experienced with matrices. identity_matrix4x4 initializes the vector floats so that the matrix has 1s on its diagonal and 0s everywhere else. transpose_matrix4x4 reverses the rows and columns in the input matrix and inverse_matrix4x4 computes the inverse of the matrix. When the inverse of matrix A, called A−1, is premultiplied by A, the product AA−1 equals the identity matrix.
No functions in this listing add or subtract matrices, but two perform multiplication. The first, scale_matrix4x4, multiplies each column of the in matrix by one of the scalars in the scale vector. For example, if scale contains {1.0, 2.0, 3.0, 4.0}, the first column of in will be unchanged, the second column will be doubled, the third will be tripled, and the fourth will be quadrupled.
The second multiplication function, mult_matrix4x4, performs traditional matrix multiplication. For the matrix equation AB = C, the top-left element of C, c11, equals the dot product of the top row of A and the leftmost column of B. Each succeeding element in the top row of C is found by multiplying the top row of A by succeeding rows of B. Elements in the lower rows of C are found by multiplying lower rows of A by succeeding rows of B.
In formal matrix notation, an element cij of the product matrix C is given by

where n is the number of elements in each row and column.
Listing 16.1 shows how these two multiplication functions are used in code. Both operate on a matrix whose element values equal the concatenation of their indices. That is, a11 = 11.0 and a24 = 24.0.
Example 16.1. Matrix Multiplication: spu_matmul.c
#include <stdio.h>
#include <libmatrix.h>
#include <spu_intrinsics.h>
int main(int argc, char **argv) {
int i, j;
vector float scale = (vector float){1.0, 2.0, 3.0, 4.0};
/* Declare 4x4 matrices, initialize input matrix */
vector float in[4], out[4];
in[0] = (vector float){11.0, 12.0, 13.0, 14.0};
in[1] = (vector float){21.0, 22.0, 23.0, 24.0};
in[2] = (vector float){31.0, 32.0, 33.0, 34.0};
in[3] = (vector float){41.0, 42.0, 43.0, 44.0};
/* Scale matrix by vector */
scale_matrix4x4(out, in, scale);
printf("Scaled Matrix:
");
for(i=0; i<4; i++) {
for(j=0; j<4; j++)
printf("%f ", spu_extract(out[i], j));
printf("
");
}
/* Multiply matrix by itself */
mult_matrix4x4(out, in, in);
printf("
Matrix Product:
");
for(i=0; i<4; i++) {
for(j=0; j<4; j++)
printf("%f ", spu_extract(out[i], j));
printf("
");
}
return 0;
}The next two functions in Table 16.3 convert vector float matrices to vector double matrices and vice versa. The last function, splat_matrix4x4, extracts each float from the input matrix and repeats it inside a separate vector float. That is, it accepts a pointer to four vector floats and returns a pointer to 16 vector floats, where each output vector contains identical scalars.
Chapter 20, “OpenGL on the Cell: Gallium and Mesa,” discusses OpenGL, an open source library for developing graphical applications. An important task in any OpenGL application is to create a viewing region. This is the space that contains the application’s graphics. Viewing regions may have two or three dimensions.
Mathematically, the viewing region is represented by a 4x4 matrix that transforms the vertices of any objects placed inside of it. This transformation is called a projection, and if the viewing region displays objects at their proper size, the projection is called orthographic. If the projection reduces an object’s size as it moves away from the viewer, it’s a perspective projection.
libmatrix provides three functions that create projection matrices. Table 16.4 lists each function, its arguments, and the purpose it serves.
Table 16.4. Projection Functions in the Matrix Library
Function Name | Purpose |
|---|---|
| Creates an orthographic projection matrix with the desired dimensions |
| Creates a perspective projection matrix with the desired dimensions |
| Creates a perspective projection matrix with the desired dimensions |
Orthographic projections are easy to understand because the viewing region is a simple box. The projection matrix transforms vertices of an object in such a way that the object is placed inside the box. This transformation does not affect the object’s size or shape. ortho_matrix4x4, creates a matrix for orthographic projection, and its arguments are the dimensions of the box. This is shown in Figure 16.2.
near and far locate the planes that bound the region in the z-direction. These are called the near and far clipping planes. By default, OpenGL places the viewer at z = 0 looking down the -z axis. So near and far identify the negative z-coordinates through which the near and far clipping planes pass.
An orthogonal projection displays each primitive at actual size, no matter where it is placed in the viewing region. But that’s not how we, as humans, view the world. From our perspective, objects get smaller as they move farther away. To display objects in this fashion, the perspective projection shrinks them as they move away from the near clipping plane.
Because objects at the far end are reduced in size, the viewing region can accommodate larger objects in back than it can in front. Therefore, the region expands as z moves from the near clipping plane toward the far clipping plane. The resulting shape is a truncated pyramid, called a frustum. This is shown in Figure 16.3.
The matrix needed to place an object within the frustum is more complex than that for the orthographic viewing region. But you don’t need to worry about generating these matrices. The last two functions in Table 16.2, frustum_matrix4x4 and perspective_matrix4x4, create them for you.
frustum_matrix4x4 accepts the same parameters as ortho_matrix4x4: left, right, bottom, top, near, and far. The viewing region is shown in Figure 16.3. left, right, bottom, and top frame the near clipping plane, whose z-coordinate is specified with near. frustum_matrix4x4 is similar to the OpenGL function, glFrustum, which accomplishes the same result.
perspective_matrix4x4 performs the same perspective projection as frustum_matrix4x4, but defines the viewing region with a different set of parameters. The first, fovy, represents the field of view angle in the y-direction. This angle is centered at the origin and touches the top and bottom of the near and far clipping planes. aspect sets the width-to-height ratio of the near clipping plane. perspective_matrix4x4 resembles the OpenGL function, gluPerspective, which uses the same parameters to perform the perspective projection.
If the camera in your game tilts, all the objects in the scene have to tilt at the same angle. This rotation is conceptually simple but mathematically complex. Table 16.5 lists the libmatrix functions that perform rotation.
Table 16.5. Matrix Library Functions for Rotation
Function Name | Purpose |
|---|---|
| Creates a 4x4 rotation matrix |
| Converts a rotation matrix to a quaternion |
| Converts a quaternion to a rotation matrix |
| Multiplies two quaternions and returns the product |
| Interpolates between two quaternions |
The first function, rotate_matrix4x4, creates a matrix that rotates points around the unit vector, axis. The rotation is counterclockwise and subtends the angle identified by angle (specified in radians). A matrix representing multiple rotations can be computed by multiplying rotation matrices together.
In the case of rotate_matrix4x4, a 4x4 matrix is required to rotate a vector of four floats. This is inefficient, particularly when an object needs to be shown moving across a range of angles. If quantization errors affect the rotation matrix, the drift can cause unpredictable results.
For this reason, many 3D developers rely on quaternions, which rotate vectors using smaller, four-element structures. But some background is necessary before the quaternion functions can be explained in full.
In 1799, a Norwegian surveyor named Caspar Wessel published the results of a major discovery: If the coordinates of two two-dimensional points are multiplied in a certain way, the resulting point has an angle equal to the sum of the angles of the two original coordinates.
This might not sound important, but Wessel’s multiplication provides an easy way to rotate a point in two dimenions. To rotate (a, b) an angle β, find the point with unit length and angle β, and multiply the two coordinates using Wessel’s method. This method is given as follows: If the second point is at (x, y), the rotation of (a, b) is located at (ax − by, ay + bx). This is shown in Figure 16.4.
Because (x, y) lies on the unit circle, x = cos(β) and y = sin(β).
The vertical axis in Figure 16.4 is labeled i, and coordinates in this space are commonly identified as x + iy. The i stands for “imaginary” because, mathematically speaking, ![]() . When you square x + iy, the result is
. When you square x + iy, the result is
(x + iy)(x + iy) = x2 + i2y2 + 2xy
Replacing i2 with −1, the new coordinate is (x2 − y2, 2xy).
Nearly fifty years after Wessel’s discovery, William Hamilton found a way to rotate three-dimensional coordinates using a method similar to Wessel’s. But rather than using x + iy, he arrived at a four-element structure, w + ix + jy + kz, where i, j, and k all equal ![]() . These structures are quaternions, and can be used to perform 3D rotation just as rotation matrices do.
. These structures are quaternions, and can be used to perform 3D rotation just as rotation matrices do.
The clockwise rotation around the unit axis vector (a, b, c) with angle θ produces a quaternion, q = {w, x, y, z}, where the components are computed as follows:

As an example, to rotate a point around the axis (1/√2, 1/2, 1/2) clockwise with an angle of 60 degrees (π/3 radians), q = {√3/2, 1/2√2, 1/4, 1/4}.
Once q is derived, the rotation of a point p can be calculated as q * p * q’, where * represents quaternion multiplication and q’ is the conjugate of q, given by {w, −x, −y, −z}. Quaternion multiplication is more complicated than matrix multiplication, but libmatrix provides a function specifically for this purpose.
OpenGL doesn’t directly support quaternions yet, so you need to create your own routines or use the functions in the SDK’s Matrix library. rot_matrix4x4_to_quat accepts a rotation matrix and returns a vector float containing the elements of a quaternion that performs the same rotation. quat_to_rot_matrix4x4 converts a vector float to a rotation matrix.
Note
Quaternion components are commonly presented as {w, x, y, z}, but the Matrix library stores quaternions as {x, y, z, w}. Remember that w is the last component.
As with rotation matrices, multiple rotations can be performed by multiplying successive quaternions. mult_quat performs this multiplication, and is needed to rotate points in space. This is shown in Listing 16.2. This application converts a rotation matrix to a quaternion and then rotates a point using both the rotation matrix and the quaternion.
Example 16.2. Coordinate Rotation: spu_rotate.c
#include <stdio.h>
#include <libmatrix.h>
#include <libvector.h>
#include <spu_intrinsics.h>
int main(int argc, char **argv) {
int i;
vector float rot_matrix[4], quat, quat_conj;
vector float axis = (vector float){.7071, .5, .5, 0};
vector float point = (vector float){2.0, 2.0, 2.0, 0};
float angle = 1.0472; /* 30 deg in radians */
/* Declare output vectors */
vector float matrix_out, quat_out;
/* Create the rotation matrix */
rotate_matrix4x4(rot_matrix, axis, angle);
/* Rotate point using the matrix */
float temp;
temp = dot_product3(rot_matrix[0], point);
matrix_out = spu_insert(temp, matrix_out, 0);
temp = dot_product3(rot_matrix[1], point);
matrix_out = spu_insert(temp, matrix_out, 1);
temp = dot_product3(rot_matrix[2], point);
matrix_out = spu_insert(temp, matrix_out, 2);
temp = dot_product3(rot_matrix[3], point);
matrix_out = spu_insert(temp, matrix_out, 3);
printf("Rotation by matrix:
");
for (i=0; i<4; i++)
printf("%f ",(float)spu_extract(matrix_out, i));
/* Convert the rotation matrix into a quaternion */
quat = rot_matrix4x4_to_quat(rot_matrix);
/* Rotate point using quaternion */
vector float conv = (vector float){-1, -1, -1, 1};
quat_conj = spu_mul(quat, conv);
quat_out = mult_quat(mult_quat(quat, point), quat_conj);
printf("
Rotation by quaternion:
");
for (i=0; i<4; i++)
printf("%f ",(float)spu_extract(quat_out, i));
printf("
");
return 0;
}
Rotation by matrix: 2.207091 1.494841 2.212257 0.000000 Rotation by quaternion: 2.207094 1.494844 2.212260 0.000000
In addition to storage efficiency and drift resistance, quaternions make it simpler to interpolate between rotations. When you want the camera to rotate smoothly from one position to the next, it’s much more efficient to update a 4-element quaternion than a 16-element rotation matrix.
Quaternion interpolation is performed by the last function in Table 16.3, slerp_quat. This returns a quaternion between the in1 and in2 quaternions, and uses the t parameter to determine how close the result should be to the inputs. For example, slerp_quat returns in1 if t = 0.0 and in2 if t = 1.0. It returns unpredictable results for t outside (0.0, 1.0).
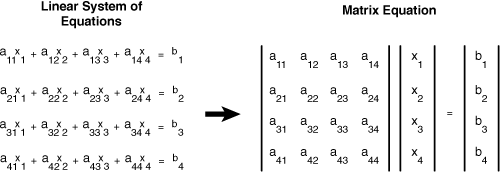
While the Matrix library functions concentrate on graphics, the routines in the Large Matrix library focus on solving linear equations. Throughout this discussion, we’ll be concerned with the equation Ax = b. Matrix A stores the coefficients of linear equations which depend on the unknown variables in vector x, and the known solutions are contained in a variable vector b. This is shown in Figure 16.5.
There are two other important differences between the Large Matrix library and the Matrix library. First, the Large Matrix library functions execute only on the SPU. Second, they can operate on matrices of any dimensionality. In many cases, the input matrices don’t even have to be square.
The liblarge_matrix functions access matrices as float arrays, and the matrix elements must be stored in row order: The first element should be a11, followed by a12, a13, and so on. Many functions need to know the matrix size and require a stride parameter that specifies the number of elements in each row. The library functions rely on SIMD operations, so stride must be a multiple of four.
The Large Matrix library functions are declared in the header liblarge_matrix.h, located in /opt/cell/sdk/src/lib/large_matrix/spu. They can be divided into two categories: basic matrix operations and matrix solution operations. This section describes both categories in detail.
Table 16.6 lists the functions in the Large Matrix library that perform simple operations: transposing, swapping, scaling, and basic arithmetic. Many of the functions operate on both vectors and matrices.
Table 16.6. Basic Matrix Operations of the Large Matrix Library
Function Name | Purpose |
|---|---|
| Returns index of the maximum element in a vector |
| Returns row index of the maximum element in the specified column |
| Sets |
| Swaps vectors |
| Swaps rows in matrix |
| Scales elements of vector |
| Scales column of matrix by |
| Multiplies elements of |
| Multiplies |
| Multiplies |
| Multiplies elements of |
| Multiplies |
| Multiplies |
The first two functions search through a vector or matrix column to find the element with the largest absolute value. The returned int is the index of this value.
transpose_matrix performs the same role as transpose_matrix4x4 in the Matrix library, and replaces rows of a matrix with columns. Because the matrix can be any size, additional parameters are needed to specify the stride, number of columns, and number of rows. swap_vectors and swap_matrix_rows operate as their names imply, but swap_matrix_rows requires explanation. Rows k1 through k2 – 1 of the matrix are swapped with the rows whose indices are pointed to by the rows parameter.
The last six functions combine matrix multiplication with addition and subtraction. As with the SPU intrinsics, madd refers to multiply and add, and nmsub refers to multiply and subtract. These functions are simple to understand and use as long as you keep track of the many parameters.
The functions in Table 16.7 rely on the functions described earlier to decompose matrices and solve systems of linear equations. In each case, matrices are accessed as float arrays, and must be accompanied by a stride value that identifies how many floats are in a row of the matrix.
Table 16.7. Large Matrix Library Functions for Matrix Decomposition and Solution
Function Name | Purpose |
|---|---|
| Decompose A (any dimensions) into upper/lower matrices and store pivot values |
| Efficiently decompose A ( |
| Solve Ax = B, where A is an |
| Solve Ax = b, where A is an |
| Solve Ax = b, where A is an |
| Solve Ax = b, where A is an |
The first two functions in the table perform LU (lower-upper) matrix decomposition, which reduces A into an upper-triangular matrix (zeros below the diagonal) and a lower-triangular matrix (ones on the diagonal, zeros above). This decomposition simplifies the process of solving linear systems by replacing Ax = B with LUx = b, which requires much less computation to solve.
The two functions, lu2_decomp and lu3_decomp_block, accept A and combine L and U into a single matrix that takes the place of A. The diagonal of the returned matrix equals the diagonal of the upper-triangular matrix, and the diagonal of the lower-triangular matrix is discarded. If A isn’t square, the L and U matrices will be upper-trapezoidal and lower-trapezoidal.
lu2_decomp performs basic LU decomposition on matrices of any dimension. It iterates through each column of the matrix and operates on the submatrix bounded by the column and the row with the same index. This operation consists of four tasks:
Find the index of the value with the greatest magnitude in the column and set this value as the pivot
Swap the row containing the pivot with the row with the same index as the current column
Scale the elements in the current column by 1/pivot
Find the product of the current row and matrix and subtract this from the submatrix
Each iteration checks whether the diagonal element is 0. If it is, the matrix is singular and the function returns the index of the row containing the 0 diagonal element. Figure 16.6 shows an example 4x4 matrix and the steps required to decompose it into LU form.
The second function in the table, lu3_decomp_block, improves the efficiency of LU decomposition by dividing the matrix into square submatrices called blocks. Then it calls lu2_decomp to decompose each block. The block size is 16 by default, which means that the matrix will be divided into 16x16 submatrices. To modify the block size, change the line
#define BLOCK_SIZE 16
in liblarge_matrix.h. This header file is located in the same directory as the liblarge_matrix library.
The rest of the functions in the table solve linear systems Ax = B, where A is stored as a matrix. A must be lower-triangular for solve_unit_lower.solve_unit_lower_1 is the same except that b is a vector. solve_upper_1 solves Ax = b, where A is upper-triangular and b is a vector. solve_linear_system_1 solves Ax = b, where A is any matrix and b is a vector.
The matrix routines described so far have all been specific to the Cell SDK, and because of this, it’s hard to compare their performance to that of similar functions running on other devices. In the late 1970s, researchers recognized the need for a baseline set of vector/matrix operations and they devised a set of standard routines. This set is called the Basic Linear Algebra Subprograms (BLAS), and this standard has become important in computational mathematics and high-performance computing.
The BLAS standard consists of over 50 routines, and you can find a full list at www.netlib.org/blas. Each function is assigned a level depending on the nature of its arguments:
Level 1 BLAS routines perform vector-vector operations such as vector arithmetic, length computation, dot product, rotation, and maximum/minimum index determination.
Level 2 BLAS routines focus on matrix-vector products, sums of matrix-vector products, and solving Ax = B linear systems.
Level 3 BLAS routines perform matrix-matrix operations, including matrix products and sums of matrix products.
BLAS routines are further distinguished by the type of vectors and matrices they accept as arguments. Different routines operate on symmetric matrices, Hermitian matrices, and complex matrices.
BLAS has been available for the PowerPC for some time, and the SDK’s BLAS library, libblas, provides PPU implementations of all BLAS functions. The BLAS library is installed by default, but there may be a problem if the SDK BLAS toolset is overwritten by the traditional PPC version. To check whether this is the case, enter the following:
find / -name blas_s.h
If the header file is available, there’s nothing to be concerned about. If it isn’t, you need to uninstall the BLAS packages as follows:
rpm -e --nodeps --allmatches blas rpm -e --nodeps --allmatches blas-devel
Then you need to reinstall the BLAS packages from the SDK. On my system, this is done with the following commands:
rpm -ivh blas-3.0-6.ppc.rpm rpm -ivh blas-devel-3.0-6.ppc.rpm
Your version numbers may differ. When you’ve finished, add the following line to /etc/yum.conf:
exclude=blas blas-devel
This will prevent these packages from being overwritten again. The blas_s.h header file should now be available in /usr/spu/include.
libblas provides an implementation of every BLAS routine for the PPU, but only a few are available to run on SPUs. Table 16.8 lists the single-precision forms of these functions.
Table 16.8. BLAS Functions Available for the SPU (Single Precision)
Purpose | |
|---|---|
| Scales the vector x by the scalar a (x = kx). |
| Copies the content of vector y into vector x (x = y). |
| Scales x by a and adds to y (y = kx + y). |
| Returns the dot product of x and y. |
| Returns the index of the largest element in x. |
| Multiplies mxn matrix A by x, scales the product by k, and adds to y (y = kAx + y). |
| Multiplies mxp matrix A by pxn matrix B, adds result to mxn matrix C (C = AB + C). |
| Multiplies 64x64 matrix A by its transpose, scale by k and add the result to C (C = kAAT + C). |
| Solves equations Ax = b where multiple b vectors are combined in the B matrix. Matrix A must be lower-triangular and nxn, B is nxm. |
| Solve equations Ax = b where multiple b vectors are combined in the B matrix. A and B must be 64x64, A must be lower-triangular. |
With the exceptions of ssyrk64x64 and strsm64x64, each of these has a double-precision equivalent that can be found my replacing the first s with a d. For example, the double-precision equivalent of isamax_spu is idamax_spu, and the equivalent of sdot_spu is ddot_spu. The signature of ddot_spu is given by the following:
double ddot_spu(double* x, double* y, int n)
This function returns a double, but most of the BLAS functions return void.
The parameter n identifies the number of elements in the vector or the number of rows/columns in a matrix. All the functions require that n be a multiple of four, but many require n to be a multiple of a higher power of two. For example, saxpy_spu requires n to be a multiple of 32 and saxpy_spu requires n to be a multiple of 16. The BLAS Programming Guide API provides more information.
strsm_spu is one of the most useful functions in Table 16.8 because it solves multiple linear systems at once. Most solvers solve Ax = b for a single vector x, but strsm_spu solves AX = B where X is a matrix, A is lower-triangular, and B contains multiple solution vectors. An example of the double-precision equivalent, dtrsm_spu, is shown in Figure 16.7.
Listing 16.3 shows how dtrsm_spu is used in code.
Example 16.3. Solving Systems of Equations: spu_blas.c
#import <stdio.h>
#import <blas_s.h>
#define B_ROWS 8
#define B_COLS 4
int main() {
double a_mat[B_ROWS*B_ROWS] __attribute__((aligned(16)));
double b_mat[B_ROWS*B_COLS] __attribute__((aligned(16)));
/* Initialize the A matrix */
int i, j;
for(i=0; i<B_ROWS; i++) {
for(j=0; j<i; j++) {
a_mat[j + i*B_ROWS] = 0.5*j+0.5;
}
a_mat[i + i*B_ROWS] = (double)1.0;
for(j=i+1; j<B_ROWS; j++) {
a_mat[j + i*B_ROWS] = 0.0;
}
}
/* Initialize the B matrix */
for(i=0; i<B_ROWS*B_COLS; i++) {
b_mat[i] = B_ROWS*B_COLS-1-i;
}
/* Solve the equations */
dtrsm_spu(B_COLS, B_ROWS, a_mat, b_mat);
/* Display the contents of the B matrix */
for(i=0; i<B_ROWS; i++) {
for(j=0; j<B_COLS; j++) {
printf("%e ",b_mat[i*B_COLS + j]);
}
printf("
");
}
printf("
");
return 0;
}The a_mat and b_mat matrices are aligned on 16-byte boundaries. For dtrsm_spu, the number of rows and columns in a_mat must be a multiple of two. The number of rows of b_mat must be a multiple of two, and the number of columns must be a multiple of four. The requirements are doubled for the single-precision function, strsm_spu.
The matrix functions discussed in this chapter only run on a single processor. But the code in the /opt/cell/sdk/src/demos/matrix_mul directory combines the PPU and SPUs to multiply large matrices together. Examining this code is important because, according to the README file, it is “highly optimized and demonstrates near-theoretical peak system performance.” The code in matrix_mul uses a number of techniques to achieve this performance and this section explains how they work.
The operation of matrix_mul consists of three main tasks:
The PPU creates the matrix and SPU contexts.
The SPUs receive information and load matrix blocks.
The SPUs process the matrix blocks and store results back to memory.
This section describes each step in detail. But before you examine the inner workings of matrix_mul, you should run the application to verify that it performs properly.
To run the matrix_mul executable, you need to enable memory access in 16MB TLB pages. These are called hugepages, and the process of configuring this feature is discussed in Appendix B, “Updating the PS3 Add-On Packages and Installing a New Linux Kernel.” When this is accomplished, allocate 24 huge pages with the following:
echo "24" > /proc/sys/vm/nr_hugepages
Then create and mount the /huge directory as follows:
mkdir /huge mount -t hugetlbfs nodev /huge
The -t hugetlbfs specifies that the directory should be mounted with the huge TLB file system, and the nodev flag ensures that the /huge directory can’t be used as a device. Finally, change the directory permissions with
chmod 755 /huge
Create a file called matrix_mul.bin in the /huge directory. This will be mapped to process memory and used to store matrix values.
matrix_mul creates three matrices: A, B, and C. Each matrix must have size n x n, where n can be 64, 128, 256, 512, 1,024, 2,048, or 4,096. The size is identified as a command-line parameter for matrix_mul, whose full description is given as
matrix_mul [-h] [-i <num>] [-m <num>] [-s <num>] [-v <num>]
Executing the command with -h explains the options available. These are
-i <num>: Performs the matrix multiplicationnumtimes (1 by default).-m <num>: Matrix size (64, 128, 256, 512, 1,024, 2,048, or 4,096) (64 by default).-s <num>: Number of SPUs to be used in the calculation (1 by default).-v <num>: Verifies num results. −1 verifies all results, 0 verifies none (0 by default).
For example, to multiply two 2048x2048 matrices using six SPUs, run the following command:
./matrix_mul -m 2048 -s 6
After allocating memory for the matrices, the PPU sets each value in A and B to a random number between 0 and 1. The SPUs will access these matrices in 64x64 blocks, so the PPU calls block_swizzle to rearrange the elements of A and B. It also creates a fourth matrix, exp, that contains the expected results of the product of A and B.
Once the matrices are initialized, the PPU creates and loads contexts for the number of SPUs specified on the command line. In each case, it obtains the address of the SPU’s problem space (see Chapter 7, “The SPE Runtime Management Library (libspe)”) and creates a variable to hold the available capacity of the SPU’s incoming mailbox. Finally, the PPU creates a thread for each context and starts the threads.
The PPU sends six mailbox messages to each SPU:
The matrix size
The number of iterations (one by default)
Address of the counters
Address of the A matrix
Address of the B matrix
Address of the C matrix
The PPU creates two counters for the SPUs. The first counts the number of blocks that have been started, and the second returns the number of blocks that have been completed.
After the messages have been sent, the PPU waits until the threads complete. Then it verifies that the C matrix matches the matrix of expected values.
When the SPUs start running, they wait for mailbox messages to arrive from the PPU. They read the PPU’s counters atomically and, if there are blocks that haven’t been processed, they increment the number of blocks started. Each block is 64*64*4 bytes = 16KB, which is the maximum size of a DMA transfer. Each SPU calls mfc_get twice: first to get a block of the A matrix, and then to get a block from the B matrix.
The SPUs use double buffering for the matrix multiplication. With each multiplication, the SPUs switch between two sets of buffers, InA/InB and OpA/OpB, and the data in one buffer pair is processed while the other buffers are filled with new data.
The main processing of the application is performed by the MatInit_MxM and MatMult_MxM functions, and a casual glance at them may leave you feeling bewildered. These functions are long and complicated, using macros that expand to macros that expand to macros. But once you see how they operate, I’m sure you’ll appreciate the structure of the algorithm and the degree of optimization used to compute A × B = C.
The first step to understanding MatInit_MxM and MatMult_MxM is to see how the matrix elements are accessed and multiplied. The A matrix is broken up into 4x4 submatrices, and each element is replicated across a vector, a00–a33. The B and C matrices are divided into vectors identified by numbers and letters. For example, the vector Bx_yA contains data in the xth row and the yth column of the A range of columns. This is shown in Figure 16.8.
An important question arises: Why use numbers and letters to denote columns in the B and C matrices? The answer is separability: While the A columns are processed, the B columns can be loaded and stored to memory. This separability is crucial in providing the algorithm’s efficiency. Remember that there are many tasks that need to be performed at once:
The C vectors must be calculated and stored to the C matrix in main memory.
The B vectors must be used in calculation and loaded from the B matrix.
The A vectors must be used in calculation, loaded from the A matrix, and shuffled.
If you look at either of the processing functions, you’ll see a number of macros with names like StageACB, StageBAC, and StageMisc. They perform essentially the same three tasks as those listed previously. The only difference between them is how different tasks are combined to take the fullest advantage of the SPU’s dual-pipeline architecture.
As an example, the StageMISCmod macro stores the A columns of the C vectors and shuffles the elements of A while computing the B columns of the C matrix. Then it switches, and computes the A columns of the C matrix while shuffling elements of the A matrix, storing elements of the C matrix, and loading elements of the B matrix. The code is monstrous to look at, but the overall goal is clear: This code multiplies, shuffles, loads, and stores data at the same time.
Once each 64x64 block is processed, the SPU calls Block_Store. This function consists of a single mfc_put that stores the submatrix of C to the appropriate position in main memory. Then the SPU updates the counter to show that a block has been finished. If more blocks need to be processed, the cycle continues. Otherwise, the SPU waits until all blocks have been completed and then stops executing.
When Arthur Cayley launched his investigations into matrix theory, he was happy to have devised a mathematical abstraction that would never be of use to anyone. But today, matrices are inescapable: They’re crucial tools for mathematicians, scientists, engineers, and programmers. The goal of this chapter has been to show that the Cell SDK provides a broad range of matrix routines that can satisfy all practitioners of matrix computation. The discussion has presented four libraries: the Vector library, the Matrix library, the Large Matrix library, and the BLAS library.
The Vector library, libvector, contains functions that operate on mathematical vectors. It provides standard functions such as the dot product and cross product, and also contains an assortment of routines for tasks like interpolation, reflection, and normalization. Many of these functions have variants ending in _v that efficiently operate on four vectors at once.
The functions in the Matrix library, libmatrix, operate only on 4x4 matrices of floats. libmatrix provides a number of basic matrix functions, but concentrates on functions for 3D graphics. Its functions create matrices for orthographic and perspective projections, and perform vector rotation using quaternions and rotation matrices.
Those not interested in 3D graphics will probably rely on functions in the Large Matrix library, liblarge_matrix. Despite the name, the routines in this library operate on matrices of any size, and the matrices can be square or nonsquare. These functions concentrate on two main aspects: matrix arithmetic and linear equation solution. The matrix arithmetic functions add, subtract, and multiply matrices. The equation solving functions perform matrix decomposition and linear system solution for both triangular and full matrices.
The functions in the BLAS library perform many of the same operations as those in other libraries, but they’re implementations of the important BLAS standard. This standard set of routines makes it possible to compare the performance of matrix operations on different systems and platforms. For the PPU, libblas provides implementations for the entire set of BLAS routines. A smaller set of functions is available to run on the SPU.