2.4. Rings
So far we have studied algebraic structures with only one operation. Now we study rings which are sets with two (compatible) binary operations. Unlike groups, these two operations are usually denoted by + and · . One can, of course, go for general notations for these operations. However, that generalization doesn’t seem to pay much, but complicates matters. We stick to the conventions.
2.4.1. Definition and Basic Properties
Definition 2.12.
|
A ring (R, +, ·) (or R in short) is a set R together with two binary operations + and · on R such that the following conditions are satisfied. As in the case of multiplicative groups we write ab for a · b.
Additive group The set R is an Abelian group under +. The additive identity is denoted by 0. · is associative (ab)c = a(bc) for every a, b, 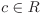 . . · is commutative ab = ba for every a,  . . Multiplicative identity There is an element (denoted by 1) in R such that a · 1 = 1 · a = a for every  . The element 1 is called the identity of R. . The element 1 is called the identity of R. Distributivity The operation · is distributive over +, that is, a(b+c) = ab + ac and (a + b)c = ac + bc for every a, b, 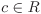 . .
|
Notice that it is more conventional to define a ring as an algebraic structure (R, +, ·) that satisfies conditions (1), (2) and (5) only. A ring (by the conventional definition) is called a commutative ring (resp. a ring with identity), if it (additionally) satisfies condition (3) (resp. (4)). As per our definition, a ring is always a commutative ring with identity. Rings that are not commutative or that do not contain the identity element are not used in the rest of the book. So let us be happy with our unconventional definition of a ring.
We do not rule out the possibility that 0 = 1 in R. In that case, for any  , we have a = a · 1 = a · 0 = 0 (See Proposition 2.6), that is to say, the set R consists of the single element 0. In this case, R is called the zero ring and is denoted (by an abuse of notation) by 0.
, we have a = a · 1 = a · 0 = 0 (See Proposition 2.6), that is to say, the set R consists of the single element 0. In this case, R is called the zero ring and is denoted (by an abuse of notation) by 0.
Finally, note that R is, in general, not a group under multiplication. This is because we do not expect a ring R to contain the multiplicative inverse of every element of R. Indeed the multiplicative inverse of the element 0 exists if and only if R = 0.
Example 2.6.
Let R be a ring and S a set. The set of all functions S → R is a ring under pointwise addition and multiplication of functions (that is, if f and g are two such functions, then we define (f + g)(a) := f(a) + g(a) and (f g)(a) := f(a)g(a) for every 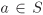 ). The additive (resp. multiplicative) identity in this ring is the constant function 0 (resp. 1). ). The additive (resp. multiplicative) identity in this ring is the constant function 0 (resp. 1). Let R be a ring. The set R[X] of all polynomials in one indeterminate X and with coefficients from R is a ring. The identity elements in R[X] are the constant polynomials 0 and 1. The addition and multiplication operations in R[X] are the standard ones on polynomials. For a non-zero polynomial 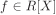 , the largest non-negative integer d for which the coefficient of Xd is non-zero is called the degree of the polynomial f and is denoted by deg f. The coefficient of Xdeg f in f is called the leading coefficient of f and is denoted by lc(f). The degree of the zero polynomial is conventionally taken to be –∞. A non-zero polynomial with leading coefficient 1 is called a monic polynomial. , the largest non-negative integer d for which the coefficient of Xd is non-zero is called the degree of the polynomial f and is denoted by deg f. The coefficient of Xdeg f in f is called the leading coefficient of f and is denoted by lc(f). The degree of the zero polynomial is conventionally taken to be –∞. A non-zero polynomial with leading coefficient 1 is called a monic polynomial. More generally, for 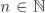 one can define the ring R[X1, . . . , Xn] of multivariate polynomials over R. Polynomial rings are of paramount importance in algebra and number theory. We devote Section 2.6 to a study of these rings. one can define the ring R[X1, . . . , Xn] of multivariate polynomials over R. Polynomial rings are of paramount importance in algebra and number theory. We devote Section 2.6 to a study of these rings. We also define the ring R(X) of rational functions over R, which consists of elements of the form f/g with f,  , g ≠ 0. More generally, the set of elements f/g with f, , g ≠ 0. More generally, the set of elements f/g with f, 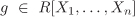 , g ≠ 0, is a ring denoted R(X1, . . . , Xn). , g ≠ 0, is a ring denoted R(X1, . . . , Xn).
|
Proposition 2.6.
|
Let R be a ring. For all a, 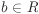 , we have: , we have:
Proof
a · 0 = a · (0 + 0) = a · 0 + a · 0, so that a · 0 = 0. Similarly, 0 · a = 0. By (1), 0 = a · 0 = a(b + (–b)) = ab + a(–b), that is, a(–b) = –ab. Similarly, (–a)b = –ab. (–a)(–b) = –(a(–b)) = –(–ab) = ab.
|
Definition 2.13.
|
Let R be a ring.
An element  is called idempotent, if a2 = a. In every ring, 0 and 1 are idempotent. The element 6 is idempotent in is called idempotent, if a2 = a. In every ring, 0 and 1 are idempotent. The element 6 is idempotent in  . It is easy to check that 0 is the only element in a ring, that is both nilpotent and idempotent. . It is easy to check that 0 is the only element in a ring, that is both nilpotent and idempotent.
|
Definition 2.14.
|
Let R be a ring.
A field R with #R finite is called a finite field. The simplest examples of finite fields are the fields 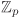 for prime integers p. In fact, it is easy to see that for prime integers p. In fact, it is easy to see that  is a field if and only if n is a prime. Finite fields are widely applied for building various cryptographic protocols. See Section 2.9 for a detailed study of finite fields. is a field if and only if n is a prime. Finite fields are widely applied for building various cryptographic protocols. See Section 2.9 for a detailed study of finite fields.
|
Corollary 2.1.
|
A field is an integral domain.
Proof
Recall from Definition 2.13 that an element in a ring cannot be simultaneously a unit and a zero-divisor.
|
Definition 2.15.
|
Let R be a non-zero ring. The characteristic of R, denoted char R, is the smallest positive integer n such that 1 + 1 + · · · + 1 (n times) = 0. If no such integer exists, then we take char R = 0.
|
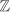 ,
,  ,
, 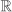 and
and  are rings of characteristic zero. If R is a non-zero finite ring, then the elements 1, 1 + 1, 1 + 1 + 1, · · · cannot be all distinct. This shows that there are positive integers m and n, m < n, such that 1+1+· · · + 1 (n times) = 1 + 1 + · · · + 1 (m times). But then 1 + 1 + · · · + 1 (n – m times) = 0. Thus any non-zero finite ring has positive (that is, non-zero) characteristic. If char R = t is finite, then for any
are rings of characteristic zero. If R is a non-zero finite ring, then the elements 1, 1 + 1, 1 + 1 + 1, · · · cannot be all distinct. This shows that there are positive integers m and n, m < n, such that 1+1+· · · + 1 (n times) = 1 + 1 + · · · + 1 (m times). But then 1 + 1 + · · · + 1 (n – m times) = 0. Thus any non-zero finite ring has positive (that is, non-zero) characteristic. If char R = t is finite, then for any 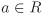 one has
one has 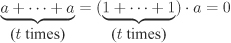 .
.
In what follows, we will often denote by n the element 1 + 1 + · · · + 1 (n times) of any ring. One should not confuse this with the integer n. One can similarly identify a negative integer –n with the ring element –(1 + 1 + · · · + 1)(n times) = (–1) + (–1) + · · · + (–1)(n times).
Proposition 2.7.
|
Let R be an integral domain of positive characteristic p. Then p is a prime.
Proof
If p is composite, then we can write p = mn with 1 < m < p and 1 < n < p. But then p = mn = 0 (in R). Since R is an integral domain, we must have m = 0 or n = 0 (in R). This contradicts the minimality of p.
|
2.4.2. Subrings, Ideals and Quotient Rings
Just as we studied subgroups of groups, it is now time to study subrings of rings. It, however, turns out that subrings are not that important for the study of rings as the subsets called ideals are. In fact, ideals (and not subrings) help us construct quotient rings. This does not mean that ideals are “normal” subrings! In fact, ideals are, in general, not subrings at all, and conversely. The formal definitions are waiting!
Definition 2.16.
|
Let R be a ring. A subset S of R is called a subring of R, if S is a ring under the ring operations of R. In this case, one calls R a superring or a ring extension of S.
If R and S are both fields, then S is often called a subfield of R and R a field extension (or simply an extension) of S. In that case, one also says that S ⊆ R is a field extension or that R is an extension over S.
|
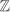 is a subring of
is a subring of 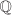 ,
,  and
and 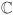 , whereas
, whereas  and
and  are field extensions.
are field extensions.
We demand that a ring always contains the multiplicative identity (Definition 2.12). This implies that if S is a subring of R, then for all integers n, the elements 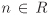 are also in S (though they need not be pairwise distinct). Similarly, if R and S are fields, then S contains all the elements of the form mn–1 for m,
are also in S (though they need not be pairwise distinct). Similarly, if R and S are fields, then S contains all the elements of the form mn–1 for m, 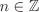 ,
, 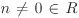 (cf. Exercise 2.26). Thus
(cf. Exercise 2.26). Thus  , the set of all even integers, is not a subring of
, the set of all even integers, is not a subring of 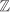 , though it is a subgroup of (
, though it is a subgroup of ( , +) (Example 2.2).
, +) (Example 2.2).
Definition 2.17.
In this book, we will use Gothic letters (usually lower case) like  ,
,  ,
,  ,
,  ,
, 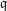 to denote ideals.
to denote ideals.
The condition for being an ideal is in one sense more stringent than that for being a subring, that is, an ideal has to be closed under multiplication by any element of the entire ring. On the other hand, we do not demand an ideal to necessarily contain the identity element 1. In fact,  is an ideal of
is an ideal of  . Conversely,
. Conversely,  is a subring of
is a subring of  but not an ideal. Subrings and ideals are different things.
but not an ideal. Subrings and ideals are different things.
Example 2.7.
Proposition 2.8.
|
The only ideals of a field are the zero ideal and the unit ideal.
Proof
By definition, every non-zero element of a field is a unit.
|
Definition 2.18.
Note that an ideal may have different generating sets of varying cardinalities. For example, the unit ideal in any ring is principal, since it is generated by 1. The integers 2 and 3 generate the unit ideal of 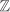 , since
, since 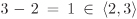 . However, neither 2 nor 3 individually generates the unit ideal of
. However, neither 2 nor 3 individually generates the unit ideal of  . Indeed, using Bézout’s relation (Proposition 2.16) one can show that for every
. Indeed, using Bézout’s relation (Proposition 2.16) one can show that for every  there is a (minimal) generating set of the unit ideal of
there is a (minimal) generating set of the unit ideal of  , that contains exactly n integers. Interested readers may try to construct such generating sets as an (easy) exercise.
, that contains exactly n integers. Interested readers may try to construct such generating sets as an (easy) exercise.
Theorem 2.6.
A very similar argument proves the following theorem. The details are left to the reader. Also see Exercise 2.31.
Theorem 2.7.
|
If K is a field, then K[X] is a principal ideal domain.
|
We now prove a very important theorem:
Theorem 2.8. Hilbert’s basis theorem
|
If R is a Noetherian ring, then so is the polynomial ring R[X1, . . . , Xn] for  . In particular, the polynomial rings . In particular, the polynomial rings  and K[X1, . . . , Xn] are Noetherian, where K is a field. and K[X1, . . . , Xn] are Noetherian, where K is a field.
Proof
Using induction on n we can reduce to the case n = 1. So we prove that if R is Noetherian, then R[X] is also Noetherian. Let  be a non-zero ideal of R[X]. Assume that be a non-zero ideal of R[X]. Assume that  is not finitely generated. Then we can inductively choose non-zero polynomials f1, f2, f3, · · · from is not finitely generated. Then we can inductively choose non-zero polynomials f1, f2, f3, · · · from  such that for each such that for each  the polynomial fi is one having the smallest degree in the polynomial fi is one having the smallest degree in  . Let di := deg fi. Then d1 ≤ d2 ≤ d3 ≤ · · ·. Let ai denote the leading coefficient of fi. Consider the ideal . Let di := deg fi. Then d1 ≤ d2 ≤ d3 ≤ · · ·. Let ai denote the leading coefficient of fi. Consider the ideal 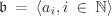 in R. By hypothesis, in R. By hypothesis,  is finitely generated, say, is finitely generated, say,  . This, in particular, implies that . This, in particular, implies that 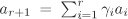 for some for some 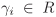 . But then the polynomial . But then the polynomial 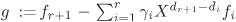 belongs to belongs to  , is non-zero and has degree < dr+1, a contradiction to the choice of fr+1. Thus , is non-zero and has degree < dr+1, a contradiction to the choice of fr+1. Thus  must be finitely generated. must be finitely generated.
|
Two particular types of ideals are very important in algebra.
Definition 2.19.
Prime and maximal ideals can be characterized by some nice equivalent criteria. See Proposition 2.9.
Definition 2.20.
|
Let R be a ring and  an ideal of R. Then an ideal of R. Then  is a subgroup of the group (R, +). Since (R, +) is Abelian, is a subgroup of the group (R, +). Since (R, +) is Abelian,  is a normal subgroup (Definition 2.6). Thus the cosets is a normal subgroup (Definition 2.6). Thus the cosets 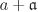 , ,  , form an additive Abelian group. We define multiplication on these cosets as , form an additive Abelian group. We define multiplication on these cosets as 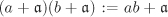 . It is easy to check that this multiplication is well-defined. Furthermore, the set of these cosets, denoted . It is easy to check that this multiplication is well-defined. Furthermore, the set of these cosets, denoted 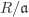 , becomes a ring under this addition and multiplication. The ring , becomes a ring under this addition and multiplication. The ring 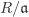 is called the quotient ring of R with respect to is called the quotient ring of R with respect to  . .
We say that two elements a, 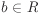 are congruent modulo an ideal are congruent modulo an ideal  (of R) and write a ≡ b (mod (of R) and write a ≡ b (mod  ), if ), if  . Thus a ≡ b (mod . Thus a ≡ b (mod  ) if and only if a and b lie in the same coset of ) if and only if a and b lie in the same coset of  , that is, , that is,  . .
|
Example 2.8.
For any ring R, the quotient ring R/0 is essentially the same as R and the quotient ring R/R is the zero ring. The ring 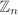 of Example 2.6 is formally defined to be the quotient ring of Example 2.6 is formally defined to be the quotient ring 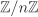 . Convince yourself that both these definitions are equivalent. . Convince yourself that both these definitions are equivalent.
|
Proposition 2.9.
|
Let R be a ring and  an ideal of R. an ideal of R.
Proof
|
The last proposition in conjunction with Corollary 2.1 indicates:
Corollary 2.2.
|
Maximal ideals are prime.
|
Corollary 2.3.
2.4.3. Homomorphisms
Recall how we have defined homomorphisms of groups. In a similar manner, we define homomorphisms of rings. A ring homomorphism is a map from one ring to another, which respects addition, multiplication and the identity element. More precisely:
Definition 2.21.
|
Let R and S be rings. A map f : R → S is called a (ring)homomorphism, if f(a+b) = f(a) + f(b) and f(ab) = f(a)f(b) for all a,  and if f(1) = 1. A homomorphism f : R → S is called an isomorphism, if there exists a homomorphism g : S → R such that g ο f = idR and f ο g = idS. As in the case of groups, bijectivity of f as a function is both necessary and sufficient for a homomorphism f : R → S to be an isomorphism. If f : R → S is an isomorphism, we write R ≅ S and say that R is isomorphic to S or that R and S are isomorphic. and if f(1) = 1. A homomorphism f : R → S is called an isomorphism, if there exists a homomorphism g : S → R such that g ο f = idR and f ο g = idS. As in the case of groups, bijectivity of f as a function is both necessary and sufficient for a homomorphism f : R → S to be an isomorphism. If f : R → S is an isomorphism, we write R ≅ S and say that R is isomorphic to S or that R and S are isomorphic.
A homomorphism f : R → R is called an endomorphism of R. An automorphism is a bijective endomorphism.
|
Example 2.9.
For any ring extension R ⊆ S, the canonical inclusion a ↦ a is a homomorphism from R → S. In particular, the identity map on any ring is an automorphism. Let R be a ring and let 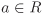 . The map R[X] → R that takes f(X) ↦ f(a) is a ring homomorphism and is called the substitution homomorphism. . The map R[X] → R that takes f(X) ↦ f(a) is a ring homomorphism and is called the substitution homomorphism. The map  taking n ↦ –n is not a ring homomorphism, since it maps 1 to –1 (and does not satisfy f(ab) = f(a)f(b) for all a, taking n ↦ –n is not a ring homomorphism, since it maps 1 to –1 (and does not satisfy f(ab) = f(a)f(b) for all a,  ). ).
|
Proposition 2.10.
|
Let f : R → S be a ring homomorphism.
If 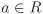 is a unit, then f(a) is a unit in S and f(a–1) = (f(a))–1. is a unit, then f(a) is a unit in S and f(a–1) = (f(a))–1.
Proof
If ab = 1, then f(a)f(b) = f(ab) = f(1) = 1.
|
The ideal  of the above proposition is called the contraction of
of the above proposition is called the contraction of  and is often denoted by
and is often denoted by 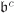 . If R ⊆ S and f is the inclusion homomorphism, then
. If R ⊆ S and f is the inclusion homomorphism, then 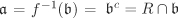 .
.
Definition 2.22.
|
Let f : R → S be a ring homomorphism. The set 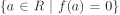 is called the kernel of f and is denoted by Ker f. The set is called the kernel of f and is denoted by Ker f. The set 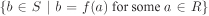 is called the image of f and is denoted by f(R) or Im f. is called the image of f and is denoted by f(R) or Im f.
|
Theorem 2.9. Isomorphism theorem
|
With the notations of the last definition, Ker f is an ideal of R, Im f is a subring of S and R/ Ker f ≅ Im f.
Proof
Consider the map 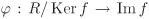 that takes a + Ker f ↦ f(a). It is easy to verify that that takes a + Ker f ↦ f(a). It is easy to verify that  is a well-defined ring homomorphism and is bijective. The details are left to the reader. Also see Theorem 2.3. is a well-defined ring homomorphism and is bijective. The details are left to the reader. Also see Theorem 2.3.
|
Definition 2.23.
Theorem 2.10. Chinese remainder theorem (CRT)
|
Let R be a ring and  . Let . Let  be ideals in R such that for all i, j, i ≠ j, the ideals be ideals in R such that for all i, j, i ≠ j, the ideals  and and  are relatively prime. Then are relatively prime. Then 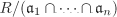 is isomorphic to the direct product is isomorphic to the direct product  . .
Proof
The assertion is obvious for n = 1. So assume that n ≥ 2 and define the map 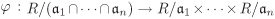 by by  for all for all  . Since . Since  for all i, the map is well-defined. It is easy to see that for all i, the map is well-defined. It is easy to see that 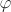 is a ring homomorphism. In order to show that is a ring homomorphism. In order to show that 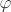 is injective, we let is injective, we let  . This means that . This means that 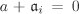 , that is, , that is,  for all i. Then for all i. Then  , that is, , that is,  . The trickier part is to prove that . The trickier part is to prove that  is surjective. Let is surjective. Let  . Let us consider the ideal . Let us consider the ideal  for each i. For a given i, there exist for each j ≠ i elements for each i. For a given i, there exist for each j ≠ i elements 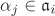 and and  with αj + βj = 1. Multiplying these equations shows that we have a with αj + βj = 1. Multiplying these equations shows that we have a 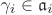 such that γi + δi = 1, where such that γi + δi = 1, where  . (This shows that . (This shows that 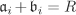 for all i.) Now consider the element for all i.) Now consider the element  . It follows that . It follows that  for all i, that is, for all i, that is, 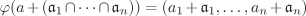 . .
|
In Section 2.5, we will see an interesting application of this theorem. Notice that the injectivity of  in the last proof does not require the coprimality of
in the last proof does not require the coprimality of  ; the surjectivity of
; the surjectivity of 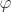 requires this condition.
requires this condition.
2.4.4. Factorization in Rings
Now we introduce the concept of divisibility in a ring. We also discuss about an important type of rings known as unique factorization domains. This study is a natural generalization of that of the rings  and K[X], K a field.
and K[X], K a field.
Definition 2.24.
|
Let R be a ring, a,  and and 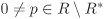 . Also let K be a field. . Also let K be a field.
A non-zero non-unit  is called a prime, if p|ab implies either p|a or p|b. One can check easily that p is prime if and only if the principal ideal 〈p〉 = pR is a prime ideal. is called a prime, if p|ab implies either p|a or p|b. One can check easily that p is prime if and only if the principal ideal 〈p〉 = pR is a prime ideal. A non-zero non-unit 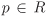 is called irreducible, if p = ab implies either a or b is a unit. is called irreducible, if p = ab implies either a or b is a unit.
|
Note that for  the concepts of prime and irreducible elements are the same. This is indeed true for any PID (Proposition 2.12). Thus our conventional definition of a prime integer p > 0 as one which has only 1 and p as (positive) divisors tallies with the definition of irreducible elements above. For the ring K[X], on the other hand, it is more customary to talk about irreducible polynomials instead of prime polynomials; they are the same thing anyway.
the concepts of prime and irreducible elements are the same. This is indeed true for any PID (Proposition 2.12). Thus our conventional definition of a prime integer p > 0 as one which has only 1 and p as (positive) divisors tallies with the definition of irreducible elements above. For the ring K[X], on the other hand, it is more customary to talk about irreducible polynomials instead of prime polynomials; they are the same thing anyway.
Proposition 2.11.
|
Let R be an integral domain and 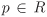 a prime. Then p is irreducible. a prime. Then p is irreducible.
Proof
Let p = ab. Then p|(ab), so that by hypothesis p|a or p|b. If p|a, then a = up for some  . Hence p = ab = upb, that is, (1 – ub)p = 0. Since R is an integral domain and p ≠ 0, we have 1 – ub = 0, that is, ub = 1, that is, b is a unit. Similarly, p|b implies a is a unit. . Hence p = ab = upb, that is, (1 – ub)p = 0. Since R is an integral domain and p ≠ 0, we have 1 – ub = 0, that is, ub = 1, that is, b is a unit. Similarly, p|b implies a is a unit.
|
Proposition 2.12.
|
Let R be a PID. An element  is prime if and only if p is irreducible. is prime if and only if p is irreducible.
Proof
[if] Let p be irreducible, but not prime. Then there are a,  such that a ∉ 〈p〉 and b ∉ 〈p〉, but such that a ∉ 〈p〉 and b ∉ 〈p〉, but  . Consider the ideal . Consider the ideal  . Since . Since 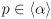 , we have p = cα for some , we have p = cα for some  . By hypothesis, p is irreducible, so that either c or α is a unit. If c is a unit, 〈p〉 = 〈α〉 = 〈p〉 + 〈a〉, that is, . By hypothesis, p is irreducible, so that either c or α is a unit. If c is a unit, 〈p〉 = 〈α〉 = 〈p〉 + 〈a〉, that is,  , a contradiction. So α is a unit. Then 〈p〉 + 〈a〉 = R which implies that there are elements u, , a contradiction. So α is a unit. Then 〈p〉 + 〈a〉 = R which implies that there are elements u,  such that up + va = 1. Similarly, there are elements u′, such that up + va = 1. Similarly, there are elements u′, 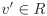 such that u′p + v′b = 1. Multiplying these two equations gives (uu′p + uv′b + u′va)p + (vv′)ab = 1. Now such that u′p + v′b = 1. Multiplying these two equations gives (uu′p + uv′b + u′va)p + (vv′)ab = 1. Now 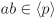 , so that ab = wp for some , so that ab = wp for some 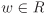 . But then (uu′p + uv′b + u′va + vv′w)p = 1, which shows that p is a unit, a contradiction. . But then (uu′p + uv′b + u′va + vv′w)p = 1, which shows that p is a unit, a contradiction.
[only if] Immediate from Proposition 2.11.
|
Definition 2.25.
|
An integral domain R is called a unique factorization domain or a UFD in short, if every non-zero element  can be written as a product a = up1 · · · pr, where can be written as a product a = up1 · · · pr, where 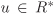 , , 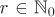 and p1, . . . , pr are prime elements (not necessarily distinct) of R. Moreover, such a factorization is unique up to permutation of the primes p1, . . . , pr and up to multiplication of the primes by units. This factorization can also be written as and p1, . . . , pr are prime elements (not necessarily distinct) of R. Moreover, such a factorization is unique up to permutation of the primes p1, . . . , pr and up to multiplication of the primes by units. This factorization can also be written as  , where , where 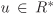 , ,  , q1, . . . , qs are pairwise non-associate primes and αi > 0 for i = 1, . . . , s. Some authors also use the term factorial ring or factorial domain in order to describe a UFD. , q1, . . . , qs are pairwise non-associate primes and αi > 0 for i = 1, . . . , s. Some authors also use the term factorial ring or factorial domain in order to describe a UFD.
If 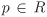 is a prime and is a prime and 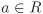 , a ≠ 0, then the multiplicity of p in a is the nonnegative integer v such that pv|a, but pv+1 a. This integer v is denoted by vp(a). It is clear form the definition that for every , a ≠ 0, then the multiplicity of p in a is the nonnegative integer v such that pv|a, but pv+1 a. This integer v is denoted by vp(a). It is clear form the definition that for every 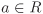 , a ≠ 0, there exist only finitely many non-associate primes p for which vp(a) > 0. , a ≠ 0, there exist only finitely many non-associate primes p for which vp(a) > 0.
|
Proposition 2.13.
|
Let R be a UFD. An element  is prime if and only if p is irreducible. is prime if and only if p is irreducible.
Proof
The only if part is immediate from Proposition 2.11. For proving the if part, let p = up1 · · · pr ( and pi primes in R) be irreducible. If r = 0, p is a unit, a contradiction. If r > 1, then p can be written as the product of two non-units up1 · · · pr–1 and pr, again a contradiction. So r = 1. and pi primes in R) be irreducible. If r = 0, p is a unit, a contradiction. If r > 1, then p can be written as the product of two non-units up1 · · · pr–1 and pr, again a contradiction. So r = 1.
|
A classical example of an integral domain that is not a UFD is  . In this ring, we have two essentially different factorizations
. In this ring, we have two essentially different factorizations  of 6 into irreducible elements. The failure of irreducible elements to be primes in such rings is a serious thing to patch up!
of 6 into irreducible elements. The failure of irreducible elements to be primes in such rings is a serious thing to patch up!
Theorem 2.11.
The converse of the above theorem is not necessarily true. For example, the polynomial ring K[X1, . . . , Xn] over a field K is a UFD for every  , but not a PID for n ≥ 2.
, but not a PID for n ≥ 2.
Divisibility in a UFD can be rephrased in terms of prime factorizations. Let R be a UFD and let the non-zero elements a,  have the prime factorizations
have the prime factorizations  and
and  with units u, u′, pairwise non-associate primes p1, . . . , pr and with αi ≥ 0 and βi ≥ 0. Then a|b if and only if αi ≤ βi for all i = 1, . . . , r. This notion leads to the following definitions.
with units u, u′, pairwise non-associate primes p1, . . . , pr and with αi ≥ 0 and βi ≥ 0. Then a|b if and only if αi ≤ βi for all i = 1, . . . , r. This notion leads to the following definitions.
Definition 2.26.
|
Let R be a UFD and let a, 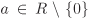 have prime factorizations as in the last paragraph. Any associate of have prime factorizations as in the last paragraph. Any associate of  , is called a greatest common divisor of a and b and is denoted by gcd(a, b). Clearly, gcd(a, b) is unique up to multiplication by units of R. Similarly, any associate of , is called a greatest common divisor of a and b and is denoted by gcd(a, b). Clearly, gcd(a, b) is unique up to multiplication by units of R. Similarly, any associate of  , is called a least common multiple of a and b and is denoted by lcm(a, b). lcm(a, b) is again unique up to multiplication by units of R. The gcd of a ≠ 0 and 0 is taken to be an associate of a, whereas gcd(0, 0) is undefined. On the other hand, lcm(a, 0) is defined to be 0 for any , is called a least common multiple of a and b and is denoted by lcm(a, b). lcm(a, b) is again unique up to multiplication by units of R. The gcd of a ≠ 0 and 0 is taken to be an associate of a, whereas gcd(0, 0) is undefined. On the other hand, lcm(a, 0) is defined to be 0 for any  . .
|
It is clear that these definitions of gcd and lcm can be readily generalized for any arbitrary finite number of elements.
Corollary 2.4.
|
Let R be a UFD and a,  not both zero. Then gcd(a, b) · lcm(a, b) is an associate of ab. not both zero. Then gcd(a, b) · lcm(a, b) is an associate of ab.
Proof
Immediate from the definitions.
|
Corollary 2.5.
|
Let R be a UFD and a, b, 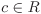 with a|bc. If gcd(a, c) = 1, then a|b. with a|bc. If gcd(a, c) = 1, then a|b.
Proof
Consider the prime factorizations of a, b and c.
|
For a PID, the gcd and lcm have equivalent characterizations.
Proposition 2.14.
|
Let R be a PID and a, b be non-zero elements of R. Let d be a gcd of a and b. Then 〈d〉 = 〈a〉 + 〈b〉. If f is an lcm of a and b, then 〈f〉 = 〈a〉 ∩ 〈b〉.
Proof
Let 〈a〉 + 〈b〉 = 〈c〉. We show that c and d are associates. There exist u, 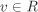 such that ua + vb = c. Since d|a and d|b, we have d|c. On the other hand, such that ua + vb = c. Since d|a and d|b, we have d|c. On the other hand, 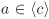 , so that c|a. Similarly c|b. Considering the prime factorizations of a and b one can then readily verify that c|d. The proof for the second part is similar and is left to the reader. , so that c|a. Similarly c|b. Considering the prime factorizations of a and b one can then readily verify that c|d. The proof for the second part is similar and is left to the reader.
|
A direct corollary to the last proposition is the following.
Corollary 2.6.
|
Let R be a PID, a,  (not both zero) and d a gcd of a and b. Then there are elements u, (not both zero) and d a gcd of a and b. Then there are elements u, 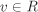 such that ua + vb = d. In particular, the ideals 〈a〉 and 〈b〉 are relatively prime if and only if gcd(a, b) is a unit. In that case, we also say that the elements a and b are relatively prime or coprime. such that ua + vb = d. In particular, the ideals 〈a〉 and 〈b〉 are relatively prime if and only if gcd(a, b) is a unit. In that case, we also say that the elements a and b are relatively prime or coprime.
|
This completes our short survey of factorization in rings. Note that 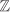 and K[X] (for a field K) are PID and hence UFD. Thus all the results we have proved in this section apply equally well to both these rings. It is because of this (and not of a mere coincidence) that these two rings enjoy many common properties. Thus our abstract treatment saves us from the duplicate effort of proving the same results once for integers (Section 2.5) and once more for polynomials (Section 2.6).
and K[X] (for a field K) are PID and hence UFD. Thus all the results we have proved in this section apply equally well to both these rings. It is because of this (and not of a mere coincidence) that these two rings enjoy many common properties. Thus our abstract treatment saves us from the duplicate effort of proving the same results once for integers (Section 2.5) and once more for polynomials (Section 2.6).
Exercise Set 2.4
| 2.21 | For a non-zero ring R, prove the following assertions:
A unit of R is not a zero-divisor. The product of two units of R is again a unit. The product of two non-units of R is again a non-unit. The element 0 is not a unit in R. The element 1 is always a unit in R. If a is a unit and ab = ac, then b = c.
Let K be a field. What are the units in the polynomial ring K[X]? In K[X1, . . . , Xn]? In the ring K(X) of rational functions? In K(X1, . . . , Xn)?
|
| 2.22 | Binomial theorem Let R be a ring, a, 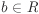 and and  . Show that . Show that
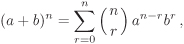
where
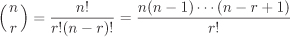
are the binomial coefficients.
|
| 2.23 | Show that every non-zero ring has a maximal (and hence prime) ideal. More generally, show that every non-unit ideal of a non-zero ring is contained in a maximal ideal. [H]
|
| 2.24 | Let R be a ring.
Show that the set of all nilpotent elements of R is an ideal of R. This ideal is usually denoted by  and is called the nilradical of R. and is called the nilradical of R. Show that the nilradical of R is the intersection of the prime ideals of R. [H]
|
| 2.25 | Show that a finite integral domain R is a field. [H]
|
| 2.26 | Let R be a ring of characteristic 0. Show that:
R contains infinitely many elements. If R is an integral domain, then R contains as subring an isomorphic copy of 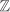 . . If R is a field, then R contains as subfield an isomorphic copy of 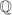 . .
|
| 2.27 | Let f : R → S be a ring-homomorphism and let  and and  be ideals in R and S respectively. Find examples to corroborate the following statements. be ideals in R and S respectively. Find examples to corroborate the following statements.
Let 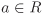 be such that f(a) is a unit in S. Then a need not be a unit in R. be such that f(a) is a unit in S. Then a need not be a unit in R. The set 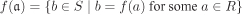 need not be an ideal of S. need not be an ideal of S.
|
| 2.28 | Let K be a field.
Show that a homomorphism from K to any non-zero ring is injective. Let L be another field and let f : K → L and g : L → K be homomorphisms such that g ο f = idK. Show that f and g are isomorphisms.
|
| 2.29 |
Show that a ring R is an integral domain if and only if 0 is a prime ideal of R. Give an example of a reduced ring that is not an integral domain. (Note that an integral domain is always reduced.)
|
| 2.30 | Let R be a ring and let  and and  be ideals of R with be ideals of R with 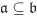 . Show that . Show that 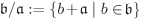 is an ideal of is an ideal of 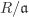 and that and that 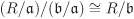 . [H] . [H]
|
| 2.31 | An integral domain R is called a Euclidean domain (ED) if there is a map 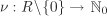 satisfying the following two conditions: satisfying the following two conditions:
ν(a) ≤ ν(ab) for all a,  . . For every a,  with b ≠ 0, there exist (not necessarily unique) q, with b ≠ 0, there exist (not necessarily unique) q, 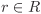 such that a = qb + r with r = 0 or ν(r) < ν(b). such that a = qb + r with r = 0 or ν(r) < ν(b).
Show that:
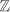 is a Euclidean domain with ν(a) = |a| for a ≠ 0. is a Euclidean domain with ν(a) = |a| for a ≠ 0.
The polynomial ring K[X] over a field K is a Euclidean domain with ν(a) = deg a for a ≠ 0. For d = –2, –1, 2, 3, the ring 
is a Euclidean domain with 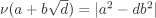 , a, , a,  , not both 0. , not both 0. A Euclidean domain is a PID (and hence a UFD).
|
| 2.32 | Let R be a ring and  an ideal. Consider the set an ideal. Consider the set
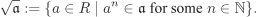
Show that 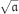 is an ideal of R. It is called the radical or root of is an ideal of R. It is called the radical or root of  . If . If  , then , then  is called a radical or a root ideal. For arbitrary ideals is called a radical or a root ideal. For arbitrary ideals  and and  of R, prove the following assertions. of R, prove the following assertions.
 . .
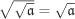 . .
If 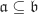 , then , then  . . If  is a prime ideal, then is a prime ideal, then 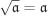 . .  if and only if if and only if  . .
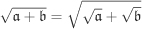 . .
 . .
The nilradical 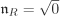 . .
|
| 2.33 | Let R be a ring. An ascending chain of ideals  is a sequence is a sequence 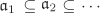 . The ascending chain is called stationary, if there is some . The ascending chain is called stationary, if there is some  such that such that  for all n ≥ n0. Show that the following conditions are equivalent. [H] for all n ≥ n0. Show that the following conditions are equivalent. [H]
R is Noetherian (that is, every ideal of R is finitely generated). Every ascending chain of ideals in R is stationary. Every non-empty set of ideals of R has a maximal element.
|
| 2.34 |
Let R be an integral domain. Define the set  . Define a relation ~ on S as (a, b) ~ (c, d) if and only if ad = bc. Show that ~ is an equivalence relation on S. Let us denote the equivalence class of . Define a relation ~ on S as (a, b) ~ (c, d) if and only if ad = bc. Show that ~ is an equivalence relation on S. Let us denote the equivalence class of  by a/b and the set of all equivalence classes of S under ~ by K. by a/b and the set of all equivalence classes of S under ~ by K. Now define (a/b)+(c/d) := (ad+bc)/(bd) and (a/b)·(c/d) := (ac)/(bd). Show that these definitions make K a field. This field is called the quotient field of R and is denoted as Q(R). This process resembles the formation of rational numbers from the integers. Indeed, 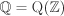 . .
|
and consider the powers α, α2, α3, . . . , we eventually get an αd which can be expressed as a linear combination of the previous (that is, smaller) powers of α. This is perhaps the reason that prompted Hilbert to call such structures “rings”. Also see Footnote 1.
![]() , we have a = a · 1 = a · 0 = 0 (See Proposition 2.6), that is to say, the set R consists of the single element 0. In this case, R is called the zero ring and is denoted (by an abuse of notation) by 0.
, we have a = a · 1 = a · 0 = 0 (See Proposition 2.6), that is to say, the set R consists of the single element 0. In this case, R is called the zero ring and is denoted (by an abuse of notation) by 0.![]() ,
, ![]() ,
, ![]() and
and ![]() are rings of characteristic zero. If R is a non-zero finite ring, then the elements 1, 1 + 1, 1 + 1 + 1, · · · cannot be all distinct. This shows that there are positive integers m and n, m < n, such that 1+1+· · · + 1 (n times) = 1 + 1 + · · · + 1 (m times). But then 1 + 1 + · · · + 1 (n – m times) = 0. Thus any non-zero finite ring has positive (that is, non-zero) characteristic. If char R = t is finite, then for any
are rings of characteristic zero. If R is a non-zero finite ring, then the elements 1, 1 + 1, 1 + 1 + 1, · · · cannot be all distinct. This shows that there are positive integers m and n, m < n, such that 1+1+· · · + 1 (n times) = 1 + 1 + · · · + 1 (m times). But then 1 + 1 + · · · + 1 (n – m times) = 0. Thus any non-zero finite ring has positive (that is, non-zero) characteristic. If char R = t is finite, then for any ![]() one has
one has ![]() .
.![]() is a subring of
is a subring of ![]() ,
, ![]() and
and ![]() , whereas
, whereas ![]() and
and ![]() are field extensions.
are field extensions.![]() are also in S (though they need not be pairwise distinct). Similarly, if R and S are fields, then S contains all the elements of the form mn–1 for m,
are also in S (though they need not be pairwise distinct). Similarly, if R and S are fields, then S contains all the elements of the form mn–1 for m, ![]() ,
, ![]() (cf. Exercise 2.26). Thus
(cf. Exercise 2.26). Thus ![]() , the set of all even integers, is not a subring of
, the set of all even integers, is not a subring of ![]() , though it is a subgroup of (
, though it is a subgroup of (![]() , +) (Example 2.2).
, +) (Example 2.2).![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() to denote ideals.[5]
to denote ideals.[5]![]() is an ideal of
is an ideal of ![]() . Conversely,
. Conversely, ![]() is a subring of
is a subring of ![]() but not an ideal. Subrings and ideals are different things.
but not an ideal. Subrings and ideals are different things.![]() , since
, since ![]() . However, neither 2 nor 3 individually generates the unit ideal of
. However, neither 2 nor 3 individually generates the unit ideal of ![]() . Indeed, using Bézout’s relation (Proposition 2.16) one can show that for every
. Indeed, using Bézout’s relation (Proposition 2.16) one can show that for every ![]() there is a (minimal) generating set of the unit ideal of
there is a (minimal) generating set of the unit ideal of ![]() , that contains exactly n integers. Interested readers may try to construct such generating sets as an (easy) exercise.
, that contains exactly n integers. Interested readers may try to construct such generating sets as an (easy) exercise.![]() of the above proposition is called the contraction of
of the above proposition is called the contraction of ![]() and is often denoted by
and is often denoted by ![]() . If R ⊆ S and f is the inclusion homomorphism, then
. If R ⊆ S and f is the inclusion homomorphism, then ![]() .
.![]() in the last proof does not require the coprimality of
in the last proof does not require the coprimality of ![]() ; the surjectivity of
; the surjectivity of ![]() requires this condition.
requires this condition.![]() and K[X], K a field.
and K[X], K a field.![]() the concepts of prime and irreducible elements are the same. This is indeed true for any PID (Proposition 2.12). Thus our conventional definition of a prime integer p > 0 as one which has only 1 and p as (positive) divisors tallies with the definition of irreducible elements above. For the ring K[X], on the other hand, it is more customary to talk about irreducible polynomials instead of prime polynomials; they are the same thing anyway.
the concepts of prime and irreducible elements are the same. This is indeed true for any PID (Proposition 2.12). Thus our conventional definition of a prime integer p > 0 as one which has only 1 and p as (positive) divisors tallies with the definition of irreducible elements above. For the ring K[X], on the other hand, it is more customary to talk about irreducible polynomials instead of prime polynomials; they are the same thing anyway.![]() . In this ring, we have two essentially different factorizations
. In this ring, we have two essentially different factorizations ![]() of 6 into irreducible elements. The failure of irreducible elements to be primes in such rings is a serious thing to patch up!
of 6 into irreducible elements. The failure of irreducible elements to be primes in such rings is a serious thing to patch up!![]() , but not a PID for n ≥ 2.
, but not a PID for n ≥ 2.![]() have the prime factorizations
have the prime factorizations ![]() and
and ![]() with units u, u′, pairwise non-associate primes p1, . . . , pr and with αi ≥ 0 and βi ≥ 0. Then a|b if and only if αi ≤ βi for all i = 1, . . . , r. This notion leads to the following definitions.
with units u, u′, pairwise non-associate primes p1, . . . , pr and with αi ≥ 0 and βi ≥ 0. Then a|b if and only if αi ≤ βi for all i = 1, . . . , r. This notion leads to the following definitions.![]() and K[X] (for a field K) are PID and hence UFD. Thus all the results we have proved in this section apply equally well to both these rings. It is because of this (and not of a mere coincidence) that these two rings enjoy many common properties. Thus our abstract treatment saves us from the duplicate effort of proving the same results once for integers (Section 2.5) and once more for polynomials (Section 2.6).
and K[X] (for a field K) are PID and hence UFD. Thus all the results we have proved in this section apply equally well to both these rings. It is because of this (and not of a mere coincidence) that these two rings enjoy many common properties. Thus our abstract treatment saves us from the duplicate effort of proving the same results once for integers (Section 2.5) and once more for polynomials (Section 2.6).