4.3. The Integer Factorization Problem
The integer factorization problem (IFP) (Problems 4.1, 4.2 and 4.3) is one of the most easily stated and yet hopelessly difficult computational problem that has attracted researchers’ attention for ages and most notably in the age of electronic computers. A huge number of algorithms varying widely in the basic strategy, mathematical sophistication and implementation intricacy have been suggested, and, in spite of these, factoring a general integer having only 1000 bits seems to be an impossible task today even using the fastest computers on earth.
It is important to note here that even proving rigorous bounds on the running times of the integer-factoring algorithms is quite often a very difficult task. In many cases, we have to be satisfied with clever heuristic bounds based on one or more reasonable but unprovable assumptions.
This section highlights human achievements in the battle against the IFP. Before going into the details of this account we want to mention some relevant points. Throughout this section we assume that we want to factor a (positive) integer n. Since such an integer can be represented by ⌈lg(n + 1)⌉ bits, the input size is taken to be lg n (or, ln n, or log n). Most modern factorization algorithms take time given by the following subexponential expression in ln n:
L(n, α, c) := exp((c + o(1))(ln n)α(ln ln n)1–α),
where 0 < α < 1 and c > 0 are constants. As described in Section 3.2, the smaller the value of α is, the closer the expression L(n, α, c) is to a polynomial expression (in ln n). If n is understood from the context, we write L(α, c) in place of L(n, α, c). Although the current best-known algorithms correspond to α = 1/3, the algorithms with α = 1/2 are also quite interesting. In this case, we use the shorter notation L[c] := L(1/2, c).
Henceforth we will use, without explicit mention, the notation q1 := 2, q2 := 3, q3 := 5, . . . to denote the sequence of primes. The concept of qt-smoothness (for some ![]() ) will often be referred to as B-smoothness, where B = {q1, . . . , qt}. Recall from Theorem 2.21 that smaller integers have higher probability of being B-smooth for a given B. This observation plays an important role in designing integer factoring algorithms. The following special case of Theorem 2.21 is often useful.
) will often be referred to as B-smoothness, where B = {q1, . . . , qt}. Recall from Theorem 2.21 that smaller integers have higher probability of being B-smooth for a given B. This observation plays an important role in designing integer factoring algorithms. The following special case of Theorem 2.21 is often useful.
Corollary 4.1.
|
Let Before any attempt of factoring n is made, it is worthwhile to check for the primality of n. Since probabilistic primality tests (like Algorithm 3.13) are quite efficient, we should first run one such test before we are sure that n is really composite. Henceforth, we will assume that n is known to be composite. |
4.3.1. Older Algorithms
“Factoring in the dark ages” (a phrase attributed to Hendrik Lenstra) used fully exponential algorithms some of which are discussed now. Though the worst-case performances of these algorithms are quite poor, there are many situations when they might factor even a large integer quite fast. It is, therefore, worthwhile to spend some time on these algorithms.
Trial division
A composite integer n admits a factor ≤ ![]() , that can be found by trial divisions of n by integers ≤
, that can be found by trial divisions of n by integers ≤ ![]() . This demands
. This demands ![]() trial divisions and is clearly impractical, even when n contains only 30 decimal digits. It is also true that n has a prime divisor ≤
trial divisions and is clearly impractical, even when n contains only 30 decimal digits. It is also true that n has a prime divisor ≤ ![]() . So it suffices to carry out trial divisions by primes only. Though this modified strategy saves us many unnecessary divisions, the asymptotic complexity does not reduce much, since by the prime number theorem the number of primes ≤
. So it suffices to carry out trial divisions by primes only. Though this modified strategy saves us many unnecessary divisions, the asymptotic complexity does not reduce much, since by the prime number theorem the number of primes ≤ ![]() is about
is about ![]() . In addition, we need to have a list of primes ≤
. In addition, we need to have a list of primes ≤ ![]() or generate the primes on the fly, neither of which is really practical. A trade-off can be made by noting that an integer m ≥ 30 cannot be prime unless m ≡ 1, 7, 11, 13, 17, 19, 23, 29 (mod 30). This means that we need to perform the trial divisions only by those integers m congruent to one of these values modulo 30 and this reduces the number of trial divisions to about 25 per cent. Though trial division is not a practical general-purpose algorithm for factoring large integers, we recommend extracting all the small prime factors of n, if any, by dividing n by a predetermined set {q1, . . . , qt} of small primes. If n is indeed qt-smooth or has all prime factors ≤ qt except only one, then the trial division method completely factors n quite fast. Even when n is not of this type, trial division might reduce its size, so that other algorithms run somewhat more efficiently.
or generate the primes on the fly, neither of which is really practical. A trade-off can be made by noting that an integer m ≥ 30 cannot be prime unless m ≡ 1, 7, 11, 13, 17, 19, 23, 29 (mod 30). This means that we need to perform the trial divisions only by those integers m congruent to one of these values modulo 30 and this reduces the number of trial divisions to about 25 per cent. Though trial division is not a practical general-purpose algorithm for factoring large integers, we recommend extracting all the small prime factors of n, if any, by dividing n by a predetermined set {q1, . . . , qt} of small primes. If n is indeed qt-smooth or has all prime factors ≤ qt except only one, then the trial division method completely factors n quite fast. Even when n is not of this type, trial division might reduce its size, so that other algorithms run somewhat more efficiently.
Pollard’s rho method
Pollard’s rho method solves the IFP in an expected O~(n1/4) time and is based on the birthday paradox (Exercise 2.172).
Let ![]() be an (unknown) prime divisor of n and let
be an (unknown) prime divisor of n and let ![]() be a random map. We start with an initial value
be a random map. We start with an initial value ![]() and generate a sequence xi+1 = f(xi),
and generate a sequence xi+1 = f(xi), ![]() , of elements of
, of elements of ![]() . Let yi denote the smallest non-negative integer satisfying yi ≡ xi (mod p). By the birthday paradox, after
. Let yi denote the smallest non-negative integer satisfying yi ≡ xi (mod p). By the birthday paradox, after ![]() iterates x1, . . . , xt are generated, we have a high chance that yi = yj, that is, xi ≡ xj (mod p) for some 1 ≤ i < j ≤ t. This means that p|(xi – xj) and computing gcd(xi – xj, n) splits n into two non-trivial factors with high probability. The method fails if this gcd is n. For a random n, this incident of having a gcd equal to n is of very low probability.
iterates x1, . . . , xt are generated, we have a high chance that yi = yj, that is, xi ≡ xj (mod p) for some 1 ≤ i < j ≤ t. This means that p|(xi – xj) and computing gcd(xi – xj, n) splits n into two non-trivial factors with high probability. The method fails if this gcd is n. For a random n, this incident of having a gcd equal to n is of very low probability.
Algorithm 4.1 gives a specific implementation of this method. Computing gcds for all the pairs (xi – xj, n) is a massive investment of time. Instead we store (in the variable ξ) the values xr, r = 2t, for ![]() and compute only gcd(xr+s – xr, n) for s = 1, . . . , r. Since the sequence yi,
and compute only gcd(xr+s – xr, n) for s = 1, . . . , r. Since the sequence yi, ![]() , is ultimately periodic with expected length of period
, is ultimately periodic with expected length of period ![]() , we eventually reach a t with r = 2t ≥ τ. In that case, the for loop detects a match. Typically, the update function f is taken to be f(x) = x2 –1 (mod n), which, though not a random function, behaves like one. Note that the iterates yi,
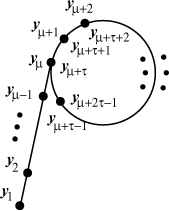
, we eventually reach a t with r = 2t ≥ τ. In that case, the for loop detects a match. Typically, the update function f is taken to be f(x) = x2 –1 (mod n), which, though not a random function, behaves like one. Note that the iterates yi, ![]() , may be visualized as being located on the Greek letter ρ as shown in Figure 4.1 (with a tail of the first μ iterates followed by a cycle of length τ). This is how this method derives its name.
, may be visualized as being located on the Greek letter ρ as shown in Figure 4.1 (with a tail of the first μ iterates followed by a cycle of length τ). This is how this method derives its name.
Figure 4.1. Iterates in Pollard’s rho method
Algorithm 4.1 takes an expected running time ![]() . Since
. Since ![]() , Pollard’s rho method runs in expected time
, Pollard’s rho method runs in expected time ![]() .
.
Algorithm 4.1. Pollard’s rho method
|
Input: A composite integer Output: A non-trivial factor of n. Steps: Choose a random element while (1) { |
Many modifications of Pollard’s rho method have been proposed in the literature. Perhaps the most notable one is an idea due to R. P. Brent. All these modifications considerably speed up Algorithm 4.1, though leaving the complexity essentially the same, that is, ![]() . We will not describe these modifications in this book.
. We will not describe these modifications in this book.
Pollard’s p – 1 method
Pollard’s p – 1 method is dependent on the prime factors of p – 1 for a prime divisor p of n. Indeed if p – 1 is rather smooth, this method may extract a (non-trivial) factor of n pretty fast, even when p itself is quite large. To start with we extend the definition of smoothness as follows.
Definition 4.1.
|
Let |
Let p be an (unknown) prime divisor of n. We may assume, without loss of generality, that ![]() . Assume that p–1 is M-power-smooth. Then (p – 1)| lcm(1, . . . , M) and, therefore, for an integer a with gcd(a, n) = 1 (and hence with gcd(a, p) = 1), we have alcm(1,...,M) ≡ 1 (mod p) by Fermat’s little theorem, that is, d := gcd(alcm(1,...,M) – 1, n) > 1. If d ≠ n, then d is a non-trivial factor of n. In case we have d = n (a very rare occurrence), we may try with another a or declare failure.
. Assume that p–1 is M-power-smooth. Then (p – 1)| lcm(1, . . . , M) and, therefore, for an integer a with gcd(a, n) = 1 (and hence with gcd(a, p) = 1), we have alcm(1,...,M) ≡ 1 (mod p) by Fermat’s little theorem, that is, d := gcd(alcm(1,...,M) – 1, n) > 1. If d ≠ n, then d is a non-trivial factor of n. In case we have d = n (a very rare occurrence), we may try with another a or declare failure.
The problem with this method is that p and so M are not known in advance. One may proceed by guessing successively increasing values of M, till the method succeeds. In the worst case, that is, when p is a safe prime, we have M = (p – 1)/2. Since ![]() , this algorithm runs in a worst-case time of
, this algorithm runs in a worst-case time of ![]() . However, if M is quite small, then this algorithm is rather efficient, irrespective of how large p itself is.
. However, if M is quite small, then this algorithm is rather efficient, irrespective of how large p itself is.
In Algorithm 4.2, we give a variant of the p – 1 method, where we supply a predetermined value of the bound M. We also assume that we have at our disposal a precalculated list of all primes q1, . . . , qt ≤ M.
There is a modification of this algorithm known as Stage 2 or the second stage. For this, we choose a second bound M′ larger than M. Assume that p – 1 = rq, where r is M-power-smooth and q is a prime in the range M < q ≤ M′. In this case, Stage 2 computes with high probability a factor of n after doing an ![]() operations as follows. When Algorithm 4.2 returns “failure” at the last step, it has already computed the value A := am (mod n), where
operations as follows. When Algorithm 4.2 returns “failure” at the last step, it has already computed the value A := am (mod n), where ![]() , ei = ⌊ln M/ln qi⌋. In this case, A has the multiplicative order of q modulo p, that is, the subgroup H of
, ei = ⌊ln M/ln qi⌋. In this case, A has the multiplicative order of q modulo p, that is, the subgroup H of ![]() generated by A has order q. We choose
generated by A has order q. We choose ![]() random integers
random integers ![]() . By the birthday paradox (Exercise 2.172), we have with high probability Ali ≡ Alj (mod p) for some i ≠ j. In that case, d := gcd(Ali – Alj, n) is divisible by p and is a desired factor of n (unless d = n, a case that occurs with a very low probability). In practice, we do not know q and so we determine s and the integers l1, . . . , ls using the bound M′ instead of q.
. By the birthday paradox (Exercise 2.172), we have with high probability Ali ≡ Alj (mod p) for some i ≠ j. In that case, d := gcd(Ali – Alj, n) is divisible by p and is a desired factor of n (unless d = n, a case that occurs with a very low probability). In practice, we do not know q and so we determine s and the integers l1, . . . , ls using the bound M′ instead of q.
Algorithm 4.2. Pollard’s p – 1 method
In another variant of Stage 2, we compute the powers Aqt+1 , . . . , Aqt′ (mod n), where qt+1, . . . , qt′ are all the primes qj satisfying M < qj ≤ M′. If p – 1 = rq is of the desired form, we would find q = qj for some t < j ≤ t′, and then gcd(Aq – 1, n), if not equal to n, would be a non-trivial factor of n.
In practice, one may try one’s luck using this algorithm for some M in the range 105 ≤ M ≤ 106 (and possibly also the second stage with 106 ≤ M′ ≤ 108) before attempting a more sophisticated algorithm like the MPQSM, the ECM or the NFSM.
Williams’ p + 1 method
As always, we assume that n is a composite integer and that p is an (unknown) prime divisor of n. Pollard’s p – 1 method uses an element a in the group ![]() whose multiplicative order is p – 1. The idea of Williams’ p + 1 method is very similar, that is, it works with an element a, this time in
whose multiplicative order is p – 1. The idea of Williams’ p + 1 method is very similar, that is, it works with an element a, this time in ![]() , whose multiplicative order is p + 1. If p + 1 is M-power-smooth for a reasonably small bound M, then computing d := gcd(ap+1 – 1, n) > 1 splits n with high probability.
, whose multiplicative order is p + 1. If p + 1 is M-power-smooth for a reasonably small bound M, then computing d := gcd(ap+1 – 1, n) > 1 splits n with high probability.
In order to find an element ![]() of order p + 1, we proceed as follows. Let α be an integer such that α2 – 4 is a quadratic non-residue modulo p. Then the polynomial
of order p + 1, we proceed as follows. Let α be an integer such that α2 – 4 is a quadratic non-residue modulo p. Then the polynomial ![]() is irreducible and
is irreducible and ![]() . Let a,
. Let a, ![]() be the two roots of f. Then ab = 1 and a + b = α. Since f(ap) = 0 (check it!) and since
be the two roots of f. Then ab = 1 and a + b = α. Since f(ap) = 0 (check it!) and since ![]() , we have ap = b = a–1, that is, ap+1 = 1.
, we have ap = b = a–1, that is, ap+1 = 1.
Unfortunately, p is not known in advance. Therefore, we represent elements of ![]() as integers modulo n and the elements of
as integers modulo n and the elements of ![]() as polynomials c0 + c1X with c0,
as polynomials c0 + c1X with c0, ![]() . Multiplying two such elements of
. Multiplying two such elements of ![]() is accomplished by multiplying the two polynomials representing these elements modulo the defining polynomial f(X), the coefficient arithmetic being that of
is accomplished by multiplying the two polynomials representing these elements modulo the defining polynomial f(X), the coefficient arithmetic being that of ![]() . This gives us a way to do exponentiations in
. This gives us a way to do exponentiations in ![]() in order to compute am – 1 for a suitable m (for example, m = lcm(1, . . . , M)).
in order to compute am – 1 for a suitable m (for example, m = lcm(1, . . . , M)).
However, the absence of knowledge of p has a graver consequence, namely, it is impossible to decide whether α2 – 4 is a quadratic non-residue modulo p for a given integer α. The only thing we can do is to try several random values of α. This is justified, because if k random integers α are tried, then the probability that for all of these α the integers α2 – 4 are quadratic residues modulo p is only 1/2k.
The code for the p + 1 method is very similar to Algorithm 4.2. We urge the reader to complete the details. Since p3 – 1 = (p – 1)(p2 + p + 1), p4 – 1 = (p2 – 1)(p2 + 1) and so on, we can work in higher extensions like ![]() ,
, ![]() to find elements of order p2 + p + 1, p2 + 1 and so on, and generalize the p ± 1 methods. However, the integers p2 + p + 1, p2 + 1, being large (compared to p ± 1), have smaller chance of being M-smooth (or M-power-smooth) for a given bound M.
to find elements of order p2 + p + 1, p2 + 1 and so on, and generalize the p ± 1 methods. However, the integers p2 + p + 1, p2 + 1, being large (compared to p ± 1), have smaller chance of being M-smooth (or M-power-smooth) for a given bound M.
The reader should have recognized why we paid attention to strong primes and safe primes (Definition 3.5, p 199, and Algorithm 3.14, p 200). Let us now concentrate on the recent developments in the IFP arena.
4.3.2. The Quadratic Sieve Method
Carl Pomerance’s quadratic sieve method (QSM) is one of the (reasonably) successful modern methods of factoring integers. Though the number field sieve factoring method is the current champion, there was a time in the recent past when the quadratic sieve method and the elliptic curve method were known to be the fastest algorithms for solving the IFP.
The basic algorithm
We assume that n is a composite integer which is not a perfect square (because it is easy to detect if n is a perfect square and if so, we replace n by ![]() ). The basic idea is to reach at a congruence of the form
). The basic idea is to reach at a congruence of the form
Equation 4.1
![]()
with x ≢ ±y (mod n). In that case, gcd(x – y, n) is a non-trivial factor of n.
We start with a factor base B = {q1, . . . , qt} comprising the first t primes and let ![]() and J := H2 – n. Then H and J are each
and J := H2 – n. Then H and J are each ![]() and hence for a small integer c the right side of the congruence
and hence for a small integer c the right side of the congruence
(H + c)2 ≡ J + 2cH + c2 (mod n)
is also ![]() . We try to factor T(c) := J + 2cH + c2 using trial divisions by elements of B. If the factorization is successful, that is, if T(c) is B-smooth, then we get a relation of the form
. We try to factor T(c) := J + 2cH + c2 using trial divisions by elements of B. If the factorization is successful, that is, if T(c) is B-smooth, then we get a relation of the form
Equation 4.2
![]()
where ![]() . (Note that T(c) ≠ 0, since n is assumed not to be a perfect square.) If all αi are even, say, αi = 2βi, then we get the desired Congruence (4.1) with
. (Note that T(c) ≠ 0, since n is assumed not to be a perfect square.) If all αi are even, say, αi = 2βi, then we get the desired Congruence (4.1) with ![]() and y = H + c. But this is rarely the case. So we keep on generating other relations. After sufficiently many relations are available, we combine these together (by multiplication) to get Congruence (4.1) and compute gcd(x – y, n). If this does not give a non-trivial factor, we try to recombine the collected relations in order to get another Congruence (4.1). This is how Pomerance’s QSM works.
and y = H + c. But this is rarely the case. So we keep on generating other relations. After sufficiently many relations are available, we combine these together (by multiplication) to get Congruence (4.1) and compute gcd(x – y, n). If this does not give a non-trivial factor, we try to recombine the collected relations in order to get another Congruence (4.1). This is how Pomerance’s QSM works.
In order to find suitable combinations for yielding Congruence (4.1), we employ a method similar to Gaussian elimination. Assume that we have collected r relations of the form

We search for integers ![]() such that the product
such that the product

is a desired Congruence (4.1). The left side of this congruence is already a square. In order to make the right side a square too, we have to essentially solve the following system of linear congruences modulo 2:
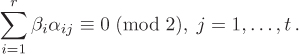
This is a system of t equations over ![]() in r unknowns β1, . . . , βr and is expected to have solutions, if r is slightly larger than t. Note that the values of αij modulo 2 are only needed for solving the above linear system. This means that we can have a compact representation of the coefficient matrix (αij) by packing 32 of the coefficients as bits per word. Gaussian elimination (over
in r unknowns β1, . . . , βr and is expected to have solutions, if r is slightly larger than t. Note that the values of αij modulo 2 are only needed for solving the above linear system. This means that we can have a compact representation of the coefficient matrix (αij) by packing 32 of the coefficients as bits per word. Gaussian elimination (over ![]() ) can be done using bit operations only.
) can be done using bit operations only.
The running time of this method can be derived using Corollary 4.1. Note that the integers T(c) that are tested for B-smoothness are O(n1/2) which corresponds to α = 1/2 in the corollary. We take qt = L[1/2] (so that t = L[1/2]/ ln L[1/2] = L[1/2] by the prime number theorem) which corresponds to β = 1/2. Assuming that the integers T(c) behave as random integers of magnitude O(n1/2), the probability that one such T(c) is B-smooth is L[–1/2]. Therefore, if L[1] values of c are tried, we expect to get L[1/2] relations involving the L[1/2] primes q1, . . . , qt. Combining these relations by Gaussian elimination is now expected to produce a non-trivial Congruence (4.1). This gives us a running-time of the order of L[3/2] for the relation collection stage. Gaussian elimination using L[1/2] unknowns also takes asymptotically the same time. However, each T(c) can have at most O(log n) distinct prime factors, implying that Relation (4.2) is necessarily sparse. This sparsity can be effectively exploited and the Gaussian elimination can be done essentially in time L[1]. Nevertheless, the entire procedure runs in time L[3/2], a subexponential expression in ln n.
Sieving
In order to reduce the running time from L[3/2] to L[1], we employ what is known as sieving (and from which the algorithm derives its name). Let us fix a priori the sieving interval, that is, the values of c for which T(c) is tested for B-smoothness, to be –M ≤ c ≤ M, where M = L[1]. Let ![]() be a small prime (that is, q = qi for some i = 1, . . . , t). We intend to find out the values of c such that qh|T(c) for small exponents h = 1, 2, . . . . Since T(c) = J + 2cH + c2 = (c + H)2 – n, the solvability for c of the condition qh|T(c) or of q|T(c) is equivalent to the solvability of the congruence (c + H)2 ≡ n (mod q). If n is a quadratic non-residue modulo q, no c satisfies the above condition. Consequently, the factor base B may comprise only those primes q for which n is a quadratic residue modulo q (instead of all primes ≤ qt). So we assume that q meets this condition. We may also assume that q n, because it is a good strategy to perform trial divisions of n by all the primes in B before we go for sieving. The sieving process makes use of an array
be a small prime (that is, q = qi for some i = 1, . . . , t). We intend to find out the values of c such that qh|T(c) for small exponents h = 1, 2, . . . . Since T(c) = J + 2cH + c2 = (c + H)2 – n, the solvability for c of the condition qh|T(c) or of q|T(c) is equivalent to the solvability of the congruence (c + H)2 ≡ n (mod q). If n is a quadratic non-residue modulo q, no c satisfies the above condition. Consequently, the factor base B may comprise only those primes q for which n is a quadratic residue modulo q (instead of all primes ≤ qt). So we assume that q meets this condition. We may also assume that q n, because it is a good strategy to perform trial divisions of n by all the primes in B before we go for sieving. The sieving process makes use of an array ![]() indexed by c. We initialize the array location
indexed by c. We initialize the array location ![]() for each c, –M ≤ c ≤ M.
for each c, –M ≤ c ≤ M.
We explain the sieving process only for an odd prime q. The modifications for the case q = 2 are left to the reader as an easy exercise. The congruence x2 – n ≡ 0 (mod q) has two distinct solutions for x, say, x1 and ![]() mod q. These correspond to two solutions for c of (H + c)2 ≡ n (mod q), namely, c1 ≡ x1 – H (mod q) and
mod q. These correspond to two solutions for c of (H + c)2 ≡ n (mod q), namely, c1 ≡ x1 – H (mod q) and ![]() (mod q). For each value of c in the interval –M ≤ c ≤ M, that is congruent either to c1 or
(mod q). For each value of c in the interval –M ≤ c ≤ M, that is congruent either to c1 or ![]() modulo q, we subtract ln q from
modulo q, we subtract ln q from ![]() . We then lift the solutions x1 and
. We then lift the solutions x1 and ![]() to the (unique) solutions x2 and
to the (unique) solutions x2 and ![]() of the congruence x2 – n ≡ 0 (mod q2) (Exercise 3.29), compute c2 ≡ x2 – H (mod q2) and
of the congruence x2 – n ≡ 0 (mod q2) (Exercise 3.29), compute c2 ≡ x2 – H (mod q2) and ![]() (mod q2) and for each c in the range –M ≤ c ≤ M congruent to c2 or
(mod q2) and for each c in the range –M ≤ c ≤ M congruent to c2 or ![]() modulo q2 subtract ln q from
modulo q2 subtract ln q from ![]() . We then again lift to obtain the solutions modulo q3 and proceed as above. We repeat this process of lifting and subtracting ln q from appropriate locations of
. We then again lift to obtain the solutions modulo q3 and proceed as above. We repeat this process of lifting and subtracting ln q from appropriate locations of ![]() until we reach a sufficiently large
until we reach a sufficiently large ![]() for which neither ch nor
for which neither ch nor ![]() corresponds to any value of c in the range –M ≤ c ≤ M. We then choose another q from the factor base and repeat the procedure explained in this paragraph for this q.
corresponds to any value of c in the range –M ≤ c ≤ M. We then choose another q from the factor base and repeat the procedure explained in this paragraph for this q.
After the sieving procedure is carried out for all small primes q in the factor base B, we check for which c, –M ≤ c ≤ M, the array location ![]() is 0. These are precisely the values of c in the indicated range for which T(c) is B-smooth. For each smooth T(c), we then compute Relation (4.2) using trial division (by primes of B).
is 0. These are precisely the values of c in the indicated range for which T(c) is B-smooth. For each smooth T(c), we then compute Relation (4.2) using trial division (by primes of B).
The sieving process replaces trial divisions (of every T(c) by every q) by subtractions (of ln q from appropriate ![]() ). This is intuitively the reason why sieving speeds up the relation collection stage. For a more rigorous analysis of the running time, note that in order to get the desired ci and
). This is intuitively the reason why sieving speeds up the relation collection stage. For a more rigorous analysis of the running time, note that in order to get the desired ci and ![]() modulo qi for each
modulo qi for each ![]() and for each i = 1, . . . , h we have either to compute a square root modulo q (for i = 1) or to solve a congruence (during lifting for i ≥ 2), each of which can be done in polynomial time. Also the bound h on the exponent of q satisfy
and for each i = 1, . . . , h we have either to compute a square root modulo q (for i = 1) or to solve a congruence (during lifting for i ≥ 2), each of which can be done in polynomial time. Also the bound h on the exponent of q satisfy ![]() , that is, h = O(log n). Finally, there are L[1/2] primes in B. Therefore, the computation of the ci and
, that is, h = O(log n). Finally, there are L[1/2] primes in B. Therefore, the computation of the ci and ![]() for all q and i takes a total of L[1/2] time.
for all q and i takes a total of L[1/2] time.
Now, we count the total number ν of subtractions of different ln q values from all the locations of the array ![]() . The size of
. The size of ![]() is 2M + 1. For each qi, we need to subtract ln q from at most 2 ⌈(2M + 1)/qi⌉ locations (for odd q), and we also have
is 2M + 1. For each qi, we need to subtract ln q from at most 2 ⌈(2M + 1)/qi⌉ locations (for odd q), and we also have ![]() . Therefore, ν is of the order of
. Therefore, ν is of the order of  , where Q is the maximum of all qi and is
, where Q is the maximum of all qi and is ![]() , and where Hm,
, and where Hm, ![]() , denote the harmonic numbers (Exercise 4.6). But Hm = O(ln m), and so ν = O(2(2M + 1) log n) = L[1], since M = L[1].
, denote the harmonic numbers (Exercise 4.6). But Hm = O(ln m), and so ν = O(2(2M + 1) log n) = L[1], since M = L[1].
The logarithms ln q (as well as the initial array values ln |T(c)|) are irrational numbers and hence need infinite precision for storing. We, however, need to work with only crude approximations of these logarithms, say up to three places after the decimal point. In that case, we cannot take ![]() as the criterion for selecting smooth values of T(c), because the approximate representation of logarithms leads to truncation (and/or rounding) errors. In practice, this is not a severe problem, because T(c) is not smooth if and only if it has a prime factor at least as large as qt+1 (the smallest prime not in B). This implies that at the end of the sieving operation the values of
as the criterion for selecting smooth values of T(c), because the approximate representation of logarithms leads to truncation (and/or rounding) errors. In practice, this is not a severe problem, because T(c) is not smooth if and only if it has a prime factor at least as large as qt+1 (the smallest prime not in B). This implies that at the end of the sieving operation the values of ![]() for smooth T(c) are close to 0, whereas those for non-smooth T(c) are much larger (close to a number at least as large as ln qt+1). Thus we may set the selection criterion for smooth integers as
for smooth T(c) are close to 0, whereas those for non-smooth T(c) are much larger (close to a number at least as large as ln qt+1). Thus we may set the selection criterion for smooth integers as ![]() or as
or as ![]() ln qt+1. It is also possible to replace floating point subtraction by integer subtraction by doing the arithmetic on 1000 times the logarithm values. To sum up, the ν = L[1] subtractions the sieving procedure does would be only single-precision operations and hence take a total of L[1] time.
ln qt+1. It is also possible to replace floating point subtraction by integer subtraction by doing the arithmetic on 1000 times the logarithm values. To sum up, the ν = L[1] subtractions the sieving procedure does would be only single-precision operations and hence take a total of L[1] time.
As mentioned earlier, Gaussian elimination with sparse equations can also be performed in time L[1]. So Pomerance’s algorithm with sieving takes time L[1].
Incomplete sieving
Numerous modifications over this basic strategy speed up the algorithm reasonably. One possibility is to do sieving every time only for h = 1 and ignore all higher powers of q. That is, for every q we check which of the integers T(c) are divisible by q and then subtract ln q from the corresponding indices of the array ![]() . If some T(c) is divisible by a higher power of q, this strategy fails to subtract ln q the required number of times. As a result, this T(c), even if smooth, may fail to pass the smoothness criterion. This problem can be overcome by increasing the cut-off from 1 (or 0.1 ln qt+1) to a value ξ ln qt for some ξ ≥ 1. But then some non-smooth T(c) will pass through the selection criterion in addition to some smooth ones that could not, otherwise, be detected. This is reasonable, because the non-smooth ones can be later filtered out from the smooth ones and one might use even trial divisions to do so. Experimentations show that values of ξ ≤ 2.5 work quite well in practice.
. If some T(c) is divisible by a higher power of q, this strategy fails to subtract ln q the required number of times. As a result, this T(c), even if smooth, may fail to pass the smoothness criterion. This problem can be overcome by increasing the cut-off from 1 (or 0.1 ln qt+1) to a value ξ ln qt for some ξ ≥ 1. But then some non-smooth T(c) will pass through the selection criterion in addition to some smooth ones that could not, otherwise, be detected. This is reasonable, because the non-smooth ones can be later filtered out from the smooth ones and one might use even trial divisions to do so. Experimentations show that values of ξ ≤ 2.5 work quite well in practice.
The reason why this strategy performs well is as follows. If q is small, for example q = 2, we should subtract only 0.693 from ![]() for every power of 2 dividing T(c). On the other hand, if q is much larger, say q = 1,299,709 (the 105-th prime), then ln q ≈ 14.078 is large. But T(c) would not, in general, be divisible by a high power of this q. This modification, therefore, leads to a situation where the probability that a smooth T(c) is actually detected as smooth is quite high. A few relations would still be missed out even with the modified selection criterion, but that is more than compensated by the speed-up gained by the method. Henceforth, we will call this modified strategy as incomplete sieving and the original strategy (of considering all powers of q) as complete sieving.
for every power of 2 dividing T(c). On the other hand, if q is much larger, say q = 1,299,709 (the 105-th prime), then ln q ≈ 14.078 is large. But T(c) would not, in general, be divisible by a high power of this q. This modification, therefore, leads to a situation where the probability that a smooth T(c) is actually detected as smooth is quite high. A few relations would still be missed out even with the modified selection criterion, but that is more than compensated by the speed-up gained by the method. Henceforth, we will call this modified strategy as incomplete sieving and the original strategy (of considering all powers of q) as complete sieving.
Large prime variation
Another trick known as large prime variation also tends to give more usable relations than are available from the original (complete or incomplete) sieving. In this context, we call a prime q′ large, if q′ ∉ B. A value of T(c) is often expected to be B-smooth except for a single large prime factor:
Equation 4.3
![]()
with q′ ∉ B. Such a value of T(c) can be easily detected. For example, incomplete sieving with the relaxed selection criterion is expected to give many such relations naturally, whereas for complete sieving, if the left-over of ln |T(c)| in ![]() at the end of the subtraction steps is < 2 ln qt, then this must correspond to a large prime factor <
at the end of the subtraction steps is < 2 ln qt, then this must correspond to a large prime factor < ![]() . Instead of throwing away an apparently unusable Equation (4.3), we may keep track of them. If a large prime q′ is not large enough (that is, not much larger than qt), then it might appear on the right side of Equation (4.3) for more than one values of c, and if that is the case, all these relations taken together now become usable for the subsequent Gaussian elimination stage (after including q′ in the factor base). This means that for each large prime occurring more frequently than once, the factor base size increases by 1, whereas the number of relations increases by at least 2. Thus with a little additional effort we enrich the factor base and the relations collected, and this, in turn, increases the probability of finding a useful Congruence (4.1), our ultimate goal. Viewed from another angle, the strategy of large prime variation allows us to start with smaller values of t and/or M and thereby speed up the sieving stage and still end up with a system capable of yielding the desired Congruence (4.1). Note that an increased factor base size leads to a larger system to solve by Gaussian elimination. But this is not a serious problem in practice, because the sieving stage (and not the Gaussian elimination stage) is usually the bottleneck of the running time of the algorithm.
. Instead of throwing away an apparently unusable Equation (4.3), we may keep track of them. If a large prime q′ is not large enough (that is, not much larger than qt), then it might appear on the right side of Equation (4.3) for more than one values of c, and if that is the case, all these relations taken together now become usable for the subsequent Gaussian elimination stage (after including q′ in the factor base). This means that for each large prime occurring more frequently than once, the factor base size increases by 1, whereas the number of relations increases by at least 2. Thus with a little additional effort we enrich the factor base and the relations collected, and this, in turn, increases the probability of finding a useful Congruence (4.1), our ultimate goal. Viewed from another angle, the strategy of large prime variation allows us to start with smaller values of t and/or M and thereby speed up the sieving stage and still end up with a system capable of yielding the desired Congruence (4.1). Note that an increased factor base size leads to a larger system to solve by Gaussian elimination. But this is not a serious problem in practice, because the sieving stage (and not the Gaussian elimination stage) is usually the bottleneck of the running time of the algorithm.
It is natural that the above discussion on handling one large prime is applicable to situations where a T(c) value has more than one large prime factors, say q′ and q″. Such a T(c) value leads to a usable relation if ![]() . This situation can be detected by a compositeness test on the non-smooth part of T(c). Subsequently, we have to factor the non-smooth part to obtain the two large primes q′ and q″. This is called two large prime variation. As the size of the integer n to be factored becomes larger, one may go for three and four large prime variations.
. This situation can be detected by a compositeness test on the non-smooth part of T(c). Subsequently, we have to factor the non-smooth part to obtain the two large primes q′ and q″. This is called two large prime variation. As the size of the integer n to be factored becomes larger, one may go for three and four large prime variations.
We will shortly encounter many other instances of sieving (for solving the IFP and the DLP). Both incomplete sieving and the use of large primes, if carefully applied, help speed up most of these sieving methods much in the same way as they do in connection with the QSM.
The multiple polynomial quadratic sieve
Easy computations (Exercise 4.11) show that the average and maximum of the integers |T(c)| checked for smoothness in the QSM are approximately M H and 2M H respectively. Though these values are theoretically ![]() , in practice the factor of M (or 2M) makes the integers |T(c)| somewhat large leading to a poor yield of B-smooth integers for larger values of |c| in the sieving interval. The multiple-polynomial quadratic sieve method (MPQSM) applies a nice trick to reduce these average and maximum values. In the original QSM, we work with a single polynomial in c, namely,
, in practice the factor of M (or 2M) makes the integers |T(c)| somewhat large leading to a poor yield of B-smooth integers for larger values of |c| in the sieving interval. The multiple-polynomial quadratic sieve method (MPQSM) applies a nice trick to reduce these average and maximum values. In the original QSM, we work with a single polynomial in c, namely,
T(c) = J + 2cH + c2 = (H + c)2 – n.
Now, we work with a more general quadratic polynomial
![]()
with W > 0 and V2 – UW = n. (The original T(c) corresponds to U = J, V = H and W = 1.) Then we have ![]() , that is, in this case a relation looks like
, that is, in this case a relation looks like
![]()
This relation has an additional factor of W that was absent in Relation (4.2). However, if W is chosen to be a prime (possibly a large one), then the Gaussian elimination stage proceeds exactly as in the original method. Indeed in this case W appears in every relation and hence poses no problem. Only the integers ![]() need to be checked for B-smoothness and hence should have small values. The sieving procedure (that is, computing the appropriate locations of
need to be checked for B-smoothness and hence should have small values. The sieving procedure (that is, computing the appropriate locations of ![]() for subtracting ln q,
for subtracting ln q, ![]() ) for the general polynomial
) for the general polynomial ![]() is very much similar to that for T(c). The details are left to the reader as an easy exercise.
is very much similar to that for T(c). The details are left to the reader as an easy exercise.
Let us now explain how we can choose the parameters U, V, W. To start with we fix a suitable sieving interval ![]() and then choose W to be a prime close to
and then choose W to be a prime close to ![]() such that n is a quadratic residue modulo W. Then we compute a square root V of n modulo W (Algorithm 3.16) and finally take U = (V2 – n)/W. This choice clearly gives
such that n is a quadratic residue modulo W. Then we compute a square root V of n modulo W (Algorithm 3.16) and finally take U = (V2 – n)/W. This choice clearly gives ![]() and
and ![]() . (Indeed one may choose 0 < V < W/2, but this is not an important issue.) Now, the maximum value of
. (Indeed one may choose 0 < V < W/2, but this is not an important issue.) Now, the maximum value of ![]() becomes
becomes ![]() . Thus even for
. Thus even for ![]() , this maximum value is smaller by a factor of
, this maximum value is smaller by a factor of ![]() than the maximum value of |T(c)| in the original QSM. Moreover, we may choose somewhat smaller values of
than the maximum value of |T(c)| in the original QSM. Moreover, we may choose somewhat smaller values of ![]() (compared to M) by working with several polynomials
(compared to M) by working with several polynomials ![]() corresponding to different choices for the prime W. This is why the MPQSM, despite having the same theoretical running-time (L[1]) as the original QSM, runs faster in practice.
corresponding to different choices for the prime W. This is why the MPQSM, despite having the same theoretical running-time (L[1]) as the original QSM, runs faster in practice.
Parallelization
The QSM is highly parallelizable. More specifically, different processors can handle pairwise disjoint subsets of B during the sieving process. That is, each processor P maintains a local array ![]() indexed by c, –M ≤ c ≤ M. The (local) sieving process at P starts with initializing all the locations
indexed by c, –M ≤ c ≤ M. The (local) sieving process at P starts with initializing all the locations ![]() to 0. For each prime q in the subset BP of the factor base B assigned to P, one adds ln q to appropriate locations (and appropriate numbers of times). After all these processors finish local sieving, a central processor computes, for each c in the sieving interval, the value ln
to 0. For each prime q in the subset BP of the factor base B assigned to P, one adds ln q to appropriate locations (and appropriate numbers of times). After all these processors finish local sieving, a central processor computes, for each c in the sieving interval, the value ln ![]() (where the sum extends over all processors P which have done local sieving) based on which T(c) is recognized as smooth or not. For the multiple-polynomial variant of the QSM, different processors might handle different polynomials
(where the sum extends over all processors P which have done local sieving) based on which T(c) is recognized as smooth or not. For the multiple-polynomial variant of the QSM, different processors might handle different polynomials ![]() and/or different subsets of B.
and/or different subsets of B.
TWINKLE: Shamir’s factoring device
Adi Shamir has proposed the complete design of a (hardware) device, TWINKLE (The Weizmann INstitute Key Location Engine), that can perform the sieving stage of QSM a hundred to thousand times faster than software implementations in usual PCs available nowadays. This speed-up is obtained by using a high clock speed (10 GHz) and opto-electronic technology for detecting smooth integers. Each TWINKLE, if mass produced, has an estimated cost of US $5,000.
The working of TWINKLE is described in Figure 4.2. It uses an opaque cylinder of a height of about 10 inches and a diameter of about 6 inches. At the bottom of the cylinder is an array of LEDs,[1] each LED representing a prime in the factor base. The i-th LED (corresponding to the i-th prime qi) emits light of intensity proportional to log qi. The device is clocked and the i-th LED emits light only during the clock cycles c for which qi|T(c). The light emitted by all the active LEDs at a given clock cycle is focused by a lens and a photo-detector senses the total emitted light. If this total light exceeds a certain threshold, the corresponding clock cycle (that is, the time c) is reported to a PC attached to TWINKLE. The PC then analyses the particular T(c) for smoothness over {q1, . . . , qt} by trial division.
[1] An LED (light emitting diode) is an electronic device that emits light, when current passes through it. A GaAs(Gallium arsenide)-based LED emits (infra-red) light of wavelength ~870 nano-meters. In the operational range of an LED, the intensity of emitted light is roughly proportional to the current passing through the LED.
Figure 4.2. Working of TWINKLE
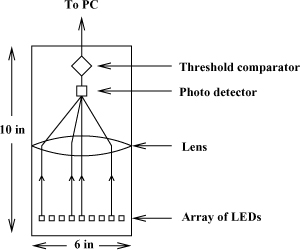
Thus, TWINKLE implements incomplete sieving by opto-electronic means. The major difference between TWINKLE’s sieving and software sieving is that in the latter we used an array of times (the c values) and the iteration went over the set of small primes. In TWINKLE, we use an array of small primes and allow time to iterate over the different values of c in the sieving interval –M ≤ c ≤ M. An electronic circuit in TWINKLE computes for each LED the cycles c at which that LED is expected to emanate light. That is to say that the i-th LED emits light only in the clock cycles c congruent modulo qi to any of the two solutions c1 and ![]() of T(c) ≡ 0 (mod qi). Shamir’s original design uses two LEDs for each prime qi, one corresponding to c1, the other to
of T(c) ≡ 0 (mod qi). Shamir’s original design uses two LEDs for each prime qi, one corresponding to c1, the other to ![]() . In that case, each LED emits light at regularly spaced clock cycles and this simplifies the electronic circuitry (at the cost of having twice the number of LEDs).
. In that case, each LED emits light at regularly spaced clock cycles and this simplifies the electronic circuitry (at the cost of having twice the number of LEDs).
Another difference of TWINKLE from software sieving is that here we add the log qi values (to zero) instead of subtracting them from log |T(c)|. By Exercise 4.11, the values |T(c)| typically have variations by small constant factors. Taking logs reduces this variation further and, therefore, comparing the sum of the active log qi values for a given c with a fixed predefined threshold (say log M H) independent of c is a neat way of bypassing the computation of all log |T(c)|, –M ≤ c ≤ M. (This strategy can also be used for software sieving.)
The reasons, why TWINKLE speeds up the sieving procedure over software implementations in conventional PCs, are the following:
Silicon-based PC chips at present can withstand clock frequencies on the order of 1 GHz. On the contrary a GaAs-based wafer containing the LED array can be clocked faster than 10 GHz.
There is no need to initialize the array
 (to log |T(c)| or zero). Similarly at the end, there is no need to compare the final values in all these array locations with a threshold.
(to log |T(c)| or zero). Similarly at the end, there is no need to compare the final values in all these array locations with a threshold.The addition of all the log qi values effective at a given c is done instantly by analog optical means. We do not require an explicit electronic adder.
Shamir [269] reports the full details of a VLSI[2] design of TWINKLE.
[2] very large-scale integration
*4.3.3. Factorization Using Elliptic Curves
H. W. Lenstra’s elliptic curve method (ECM) is another modern algorithm to solve the IFP and runs in expected time ![]() , where p is the smallest prime factor of n (the integer to be factored). Since
, where p is the smallest prime factor of n (the integer to be factored). Since ![]() , this running time is L[1] = L(n, 1/2, 1): that is, the same as the QSM. However, if p is small (that is, if p = O(nα) for some α < 1/2), then the ECM is expected to outperform the QSM, since the working of the QSM is incapable of exploiting smaller values of p.
, this running time is L[1] = L(n, 1/2, 1): that is, the same as the QSM. However, if p is small (that is, if p = O(nα) for some α < 1/2), then the ECM is expected to outperform the QSM, since the working of the QSM is incapable of exploiting smaller values of p.
As before, let n be a composite natural number having no small prime divisors and let p be the smallest prime divisor of n. For denoting subexponential expressions in ln p, we use the symbol Lp[c] := L(p, 1/2, c), whereas the unsubscripted symbol L[c] stands for L(n, 1/2, c). We work with random elliptic curves
![]()
and consider the group ![]() of rational points on E modulo p. However, since p is not known a priori, we intend to work modulo n. The canonical surjection
of rational points on E modulo p. However, since p is not known a priori, we intend to work modulo n. The canonical surjection ![]() allows us to identify the
allows us to identify the ![]() -rational points on E as points on E over
-rational points on E as points on E over ![]() . We now define a bound
. We now define a bound ![]() and let B = {q1, . . . , qt} be all the primes smaller than or equal to M, so that by the prime number theorem (Theorem 2.20) #B ≈ M/ln
and let B = {q1, . . . , qt} be all the primes smaller than or equal to M, so that by the prime number theorem (Theorem 2.20) #B ≈ M/ln ![]() . Of course, p is not known in advance, so that M and B are also not known. We will discuss about the choice of M and B later. For the time being, let us assume that we know some approximate value of p, so that M and B can be fixed, at least approximately, ate the beginning of the algorithm.
. Of course, p is not known in advance, so that M and B are also not known. We will discuss about the choice of M and B later. For the time being, let us assume that we know some approximate value of p, so that M and B can be fixed, at least approximately, ate the beginning of the algorithm.
By Hasse’s theorem (Theorem 2.48, p 106), the cardinality ![]() satisfies
satisfies ![]() , that is, ν = O(p). If we make the heuristic assumption that ν is a random integer on the order O(p), then Corollary 4.1 tells us that ν is B-smooth with probability
, that is, ν = O(p). If we make the heuristic assumption that ν is a random integer on the order O(p), then Corollary 4.1 tells us that ν is B-smooth with probability ![]() . This assumption is certainly not rigorous, but accepting it gives us a way to analyse the running time of the algorithm.
. This assumption is certainly not rigorous, but accepting it gives us a way to analyse the running time of the algorithm.
If ![]() random curves are tried, then we expect to find one B-smooth value of ν. In this case, a non-trivial factor of n can be computed with high probability as follows. Define ei := ⌊ln n/ln qi⌋ for i = 1, . . . , t, and
random curves are tried, then we expect to find one B-smooth value of ν. In this case, a non-trivial factor of n can be computed with high probability as follows. Define ei := ⌊ln n/ln qi⌋ for i = 1, . . . , t, and ![]() , where t is the number of primes in B. If ν is B-smooth, then ν|m and, therefore, for any point
, where t is the number of primes in B. If ν is B-smooth, then ν|m and, therefore, for any point ![]() we have
we have ![]() . Computation of mP involves computation of many sums P1 + P2 of points P1 := (h1, k1) and P2 := (h2, k2). At some point of time, we would certainly compute
. Computation of mP involves computation of many sums P1 + P2 of points P1 := (h1, k1) and P2 := (h2, k2). At some point of time, we would certainly compute ![]() , that is, P1 = –P2, that is, h1 ≡ h2 (mod p) and k1 ≡ –k2 (mod p). Since p was unknown, we worked modulo n, that is, the values of h1, h2, k1 and k2 are known modulo n. Let d := gcd(h1 – h2, n). Then p|d and if d ≠ n (the case d = n has a very small probability!), we have the non-trivial factor d of n. The computation of the coordinates of P1 + P2 (assuming P1 ≠ P2) demands computing the inverse of h1 – h2 modulo n (Section 2.11.2). However, if d = gcd(h1 – h2, n) ≠ 1, then this inverse does not exist and so the computation of P1 + P2 fails, and we have a non-trivial factor of n. If ν is B-smooth, then the computation of mP is bound to fail. The basic steps of the ECM are then as shown in Algorithm 4.3.
, that is, P1 = –P2, that is, h1 ≡ h2 (mod p) and k1 ≡ –k2 (mod p). Since p was unknown, we worked modulo n, that is, the values of h1, h2, k1 and k2 are known modulo n. Let d := gcd(h1 – h2, n). Then p|d and if d ≠ n (the case d = n has a very small probability!), we have the non-trivial factor d of n. The computation of the coordinates of P1 + P2 (assuming P1 ≠ P2) demands computing the inverse of h1 – h2 modulo n (Section 2.11.2). However, if d = gcd(h1 – h2, n) ≠ 1, then this inverse does not exist and so the computation of P1 + P2 fails, and we have a non-trivial factor of n. If ν is B-smooth, then the computation of mP is bound to fail. The basic steps of the ECM are then as shown in Algorithm 4.3.
Algorithm 4.3. Elliptic curve method (ECM)
|
Input: A composite integer Output: A non-trivial divisor d of n. Steps: while (1) { |
Before we derive the running time of the ECM, some comments are in order. A random curve E is chosen by selecting random integers a and b modulo n. It turns out that taking a as single-precision integers and b = 1 works quite well in practice. Indeed one can keep on trying the values a = 0, 1, 2, . . . successively. Note that the curve E is an elliptic curve, that is, non-singular, if and only if δ := gcd(n, 4a3 + 27b2) = 1. However, having δ > 1 is an extremely rare occurrence and one might skip the computation of δ before starting the trial with a curve. The choice b = 1 is attractive, because in that case we may take the point P = (0, 1). In Section 3.6, we have described a strategy to find a random point on an elliptic curve over a field K. This is based on the assumption that computing square roots in K is easy. The same method can be applied to curves over ![]() , but n being composite, it is difficult to compute square roots modulo n. So taking b to be 1 (or the square of a known integer) is indeed a pragmatic decision. After all, we do not need P to be a random point on E.
, but n being composite, it is difficult to compute square roots modulo n. So taking b to be 1 (or the square of a known integer) is indeed a pragmatic decision. After all, we do not need P to be a random point on E.
Recall that we have taken ![]() , where ei = ⌊ln n/ln qi⌋. If instead we take ei := ⌊ln M/ln qi⌋ (where M is the bound mentioned earlier), the computation of mP per trial reduces much, whereas the probability of a successful trial (that is, a failure of computing mP) does not decrease much. The integer m can be quite large. One, however, need not compute m explicitly, but proceed as follows: first take Q0 := P and subsequently for each i = 1, . . . , t compute
, where ei = ⌊ln n/ln qi⌋. If instead we take ei := ⌊ln M/ln qi⌋ (where M is the bound mentioned earlier), the computation of mP per trial reduces much, whereas the probability of a successful trial (that is, a failure of computing mP) does not decrease much. The integer m can be quite large. One, however, need not compute m explicitly, but proceed as follows: first take Q0 := P and subsequently for each i = 1, . . . , t compute ![]() . One finally gets mP = Qt.
. One finally gets mP = Qt.
Now comes the analysis of the running time of the ECM. We have fixed the parameter M to be ![]() , so that B contains
, so that B contains ![]() small primes. The most expensive part of a trial with a random elliptic curve is the (attempted) computation of the point mP. This involves
small primes. The most expensive part of a trial with a random elliptic curve is the (attempted) computation of the point mP. This involves ![]() additions of points. Since an expected number of
additions of points. Since an expected number of ![]() elliptic curves needs to be tried for finding a non-trivial factor of n, the algorithm performs an expected number of
elliptic curves needs to be tried for finding a non-trivial factor of n, the algorithm performs an expected number of ![]() additions of points on curves modulo n. Since each such addition can be done in polynomial time, the announced running time follows.
additions of points on curves modulo n. Since each such addition can be done in polynomial time, the announced running time follows.
Note that ![]() is the optimal running time of the ECM and can be shown to be achieved by taking
is the optimal running time of the ECM and can be shown to be achieved by taking ![]() . But, in practice, p is not known a priori. Various ad hoc ways may be adopted to get around with this difficulty. One possibility is to use the worst-case bound
. But, in practice, p is not known a priori. Various ad hoc ways may be adopted to get around with this difficulty. One possibility is to use the worst-case bound ![]() . For example, for factoring integers of the form n = pq, where p and q are primes of roughly the same size, this is a good approximation for p. Another strategy is to start with a small value of M and increase M gradually with the number of trials performed. For larger values of M, the probability of a successful trial increases implying that less number of elliptic curves needs to be tried, whereas the time per iteration (that is, for the computation of mP) increases. In other words, the total running time of the ECM is apparently not very sensitive to the choice of M.
. For example, for factoring integers of the form n = pq, where p and q are primes of roughly the same size, this is a good approximation for p. Another strategy is to start with a small value of M and increase M gradually with the number of trials performed. For larger values of M, the probability of a successful trial increases implying that less number of elliptic curves needs to be tried, whereas the time per iteration (that is, for the computation of mP) increases. In other words, the total running time of the ECM is apparently not very sensitive to the choice of M.
A second stage can be used for each elliptic curve in order to increase the probability of a trial being successful. A strategy very similar to the second stage of the p – 1 method can be employed. The reader is urged to fill out the details. Employing the second stage leads to reasonable speed-up in practice, though it does not affect the asymptotic running time.
The ECM can be effectively parallelized, since different processors can carry out the trials, that is, computations of mP (together with the second stage) with different sets of (random) elliptic curves.
**4.3.4. The Number Field Sieve Method
The number field sieve method (NFSM) is till date the most successful of all integer factoring algorithms. Under certain heuristic assumptions it achieves a running time of the form L(n, 1/3, c), which is better than the L(n, 1/2, c′) algorithms described so far. The NFSM was first designed for integers of a special form. This variant of the NFSM is called the special NFS method (SNFSM) and was later modified to the general NFS method (GNFSM) that can handle arbitrary integers. The running time of the SNFSM has c = (32/9)1/3 ≈ 1.526, whereas that for the GNFSM has c = (64/9)1/3 ≈ 1.923. For the sake of simplicity, we describe only the SNFSM in this book (see Cohen [56] and Lenstra and Lenstra [165] for further details).
We choose an integer ![]() and a polynomial
and a polynomial ![]() such that f(m) ≡ 0 (mod n). We assume that f is irreducible in
such that f(m) ≡ 0 (mod n). We assume that f is irreducible in ![]() ; otherwise a non-trivial factor of f yields a non-trivial factor of n. Consider the number field
; otherwise a non-trivial factor of f yields a non-trivial factor of n. Consider the number field ![]() . Let d := deg f be the degree of the number field K. We use the complex embedding
. Let d := deg f be the degree of the number field K. We use the complex embedding ![]() for some root
for some root ![]() of f. The special NFS method makes certain simplifying assumptions:
of f. The special NFS method makes certain simplifying assumptions:
f is monic, so that
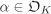 .
. is monogenic.
is monogenic. is a PID.
is a PID.
Consider the ring homomorphism
![]()
This is well-defined, since f(m) ≡ 0 (mod n). We choose small coprime (rational) integers a, b and note that Φ(a+bα) = a + bm (mod n). Let ![]() be a predetermined smoothness bound. Assume that for a given pair (a, b), both a + bm and a + bα are B-smooth. For the rational integer a + bm, this means
be a predetermined smoothness bound. Assume that for a given pair (a, b), both a + bm and a + bα are B-smooth. For the rational integer a + bm, this means
![]()
![]() being the set of all rational primes ≤ B. On the other hand, smoothness of the algebraic integer a + bα means that the principal ideal
being the set of all rational primes ≤ B. On the other hand, smoothness of the algebraic integer a + bα means that the principal ideal ![]() is a product of prime ideals of prime norms ≤ B; that is, we have a factorization
is a product of prime ideals of prime norms ≤ B; that is, we have a factorization
![]()
where ![]() is the set of all prime ideals of
is the set of all prime ideals of ![]() of prime norms ≤ B. By assumption, each
of prime norms ≤ B. By assumption, each ![]() is a principal ideal. Let
is a principal ideal. Let ![]() denote a set of generators, one for each ideal in
denote a set of generators, one for each ideal in ![]() . Further let
. Further let ![]() denote a set of generators of the multiplicative group of units of
denote a set of generators of the multiplicative group of units of ![]() . The smoothness of a + bα can, therefore, be rephrased as
. The smoothness of a + bα can, therefore, be rephrased as
Equation 4.4
![]()
Applying Φ then yields
![]()
This is a relation for the SNFSM. After ![]() relations are available, Gaussian elimination modulo 2 (as in the case of the QSM) is expected to give us a congruence of the form
relations are available, Gaussian elimination modulo 2 (as in the case of the QSM) is expected to give us a congruence of the form
x2 ≡ y2 (mod n),
and gcd(x – y, n) is possibly a non-trivial factor of n. This is the basic strategy of the SNFSM. We clarify some details now.
Selecting the polynomial f(X)
There is no clearly specified way to select the polynomial f for defining the number field ![]() . We require f to have small coefficients. Typically, m is much smaller than n and one writes the expansion of n in base m as n = btmt + bt–1mt–1 + ··· + b1m + b0 with 0 ≤ bi < m. Taking f(X) = btXt + bt–1Xt–1 + ··· + b1X + b0 is often suggested.
. We require f to have small coefficients. Typically, m is much smaller than n and one writes the expansion of n in base m as n = btmt + bt–1mt–1 + ··· + b1m + b0 with 0 ≤ bi < m. Taking f(X) = btXt + bt–1Xt–1 + ··· + b1X + b0 is often suggested.
For integers n of certain special forms, we have natural choices for f. The seminal paper on the NFSM by Lenstra et al. [167] assumes that n = re – s for a small integer ![]() and a non-zero integer s with small absolute value. In this case, one first chooses a small extension degree
and a non-zero integer s with small absolute value. In this case, one first chooses a small extension degree ![]() and sets m := r⌈e/d⌉ and f(X) := Xd – sr⌈e/d⌉d–e. Typically, d = 5 works quite well in practice. Lenstra et al. report the implementation of the SNFSM for factoring n = 3239 – 1. The parameters chosen are d = 5, m = 348 and f(X) = X5 – 3. In this case,
and sets m := r⌈e/d⌉ and f(X) := Xd – sr⌈e/d⌉d–e. Typically, d = 5 works quite well in practice. Lenstra et al. report the implementation of the SNFSM for factoring n = 3239 – 1. The parameters chosen are d = 5, m = 348 and f(X) = X5 – 3. In this case, ![]() is monogenic and a PID.
is monogenic and a PID.
Construction of 
Take a small rational prime ![]() . From Section 2.13, it follows that if
. From Section 2.13, it follows that if ![]() is the factorization of the canonical image of f(X) modulo p, then
is the factorization of the canonical image of f(X) modulo p, then ![]() , i = 1, . . . , r, are all the primes lying over p. We have also seen that
, i = 1, . . . , r, are all the primes lying over p. We have also seen that ![]() ,
, ![]() , is prime if and only if di = 1, that is,
, is prime if and only if di = 1, that is, ![]() for some
for some ![]() . Thus, each root of
. Thus, each root of ![]() in
in ![]() corresponds to a prime ideal of
corresponds to a prime ideal of ![]() of prime norm p.
of prime norm p.
To sum up, a prime ideal in ![]() of prime norm is specified by a pair (p, cp) of values (in
of prime norm is specified by a pair (p, cp) of values (in ![]() ). We denote this ideal by
). We denote this ideal by ![]() . All ideals in
. All ideals in ![]() can be precomputed by finding the roots of the defining polynomial f(X) modulo the small primes p ≤ B. One can use the root-finding algorithms of Exercise 3.29.
can be precomputed by finding the roots of the defining polynomial f(X) modulo the small primes p ≤ B. One can use the root-finding algorithms of Exercise 3.29.
Construction of 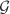
Constructing a set ![]() of generators of ideals in
of generators of ideals in ![]() is a costly operation. We have just seen that each prime ideal
is a costly operation. We have just seen that each prime ideal ![]() of
of ![]() corresponds to a pair (p, cp) and is a principal ideal by assumption. A generator
corresponds to a pair (p, cp) and is a principal ideal by assumption. A generator ![]() of such an ideal
of such an ideal ![]() is an element of the form
is an element of the form ![]() ,
, ![]() , with N(gp,cp) = ±p and
, with N(gp,cp) = ±p and ![]() (mod p). Algorithm 4.4 (quoted from Lenstra et al. [167]) computes the generators gp,cp for all relevant pairs (p, cp). The first for loop exhaustively searches over all small polynomials h(α) in order to locate for each (p, cp) an element
(mod p). Algorithm 4.4 (quoted from Lenstra et al. [167]) computes the generators gp,cp for all relevant pairs (p, cp). The first for loop exhaustively searches over all small polynomials h(α) in order to locate for each (p, cp) an element ![]() of norm kp with |k| as small as possible. If the smallest k (stored in ap,cp) is ±1,
of norm kp with |k| as small as possible. If the smallest k (stored in ap,cp) is ±1, ![]() is already a generator gp,cp of
is already a generator gp,cp of ![]() , else some additional adjustments need to be performed.
, else some additional adjustments need to be performed.
Algorithm 4.4. Construction of generators of ideals for the SNFSM
Construction of 
Let K have the signature (r1, r2). Write ρ = r1 + r2 – 1. By Dirichlet’s unit theorem, the group ![]() of units of
of units of ![]() is generated by an appropriate root u0 of unity and ρ multiplicatively independent[3] elements u1, . . . , uρ of infinite order. Each unit u of
is generated by an appropriate root u0 of unity and ρ multiplicatively independent[3] elements u1, . . . , uρ of infinite order. Each unit u of ![]() has norm N(u) = ±1. Thus, one may keep on generating elements
has norm N(u) = ±1. Thus, one may keep on generating elements ![]() , hi small integers, of norm ±1, until ρ independent elements are found. Many elements of
, hi small integers, of norm ±1, until ρ independent elements are found. Many elements of ![]() are available as a by-product during the construction of
are available as a by-product during the construction of ![]() , which involves the computation of norms of many elements in
, which involves the computation of norms of many elements in ![]() . For a more general exposition on this topic, see Algorithm 6.5.9 of Cohen [56].
. For a more general exposition on this topic, see Algorithm 6.5.9 of Cohen [56].
[3] The elements u1, . . . , uρ in a (multiplicatively written) group are called (multiplicatively) independent if
,
, is the group identity only for n1 = ··· = nρ = 0.
Computing the factorization of a + bα
In order to compute the factorization of Equation (4.4), we first factor the integer N(a + bα) = bdf(–a/b). If ![]() is the prime factorization of 〈a + bα〉 with pairwise distinct prime ideals
is the prime factorization of 〈a + bα〉 with pairwise distinct prime ideals ![]() of
of ![]() , by the multiplicative property of norms we obtain
, by the multiplicative property of norms we obtain ![]() .
.
Now, let p ≤ B be a small prime. If p N(a + bα), it is clear that no prime ideal of ![]() of norm p (or a power of p) appears in the factorization of 〈a + bα〉. On the other hand, if p| N(a + bα), then
of norm p (or a power of p) appears in the factorization of 〈a + bα〉. On the other hand, if p| N(a + bα), then ![]() for some
for some ![]() . The assumption
. The assumption ![]() implies that the inertial degree of
implies that the inertial degree of ![]() is 1: that is,
is 1: that is, ![]() , that is,
, that is, ![]() , that is, there is a cp with f(cp) ≡ 0 (mod p) such that the prime ideal
, that is, there is a cp with f(cp) ≡ 0 (mod p) such that the prime ideal ![]() corresponds to the pair (p, cp). In this case, we have a ≡ –cpb (mod p). Assume that another prime ideal
corresponds to the pair (p, cp). In this case, we have a ≡ –cpb (mod p). Assume that another prime ideal ![]() of norm p appears in the prime factorization of 〈a + bα〉. If
of norm p appears in the prime factorization of 〈a + bα〉. If ![]() corresponds to the pair p,
corresponds to the pair p, ![]() , then
, then ![]() . Since cp and
. Since cp and ![]() are distinct modulo p, it follows that p|gcd(a, b), a contradiction, since gcd(a, b) = 1. Thus, a unique ideal
are distinct modulo p, it follows that p|gcd(a, b), a contradiction, since gcd(a, b) = 1. Thus, a unique ideal ![]() of norm p appears in the factorization of 〈a + bα〉. Moreover, the multiplicity of
of norm p appears in the factorization of 〈a + bα〉. Moreover, the multiplicity of ![]() in the factorization of 〈a + bα〉 is the same as the multiplicity vp(N(a + bα)).
in the factorization of 〈a + bα〉 is the same as the multiplicity vp(N(a + bα)).
Thus, one may attempt to factorize N(a + bα) using trial divisions by primes ≤ B. If the factorization is successful, that is, if N(a + bα) is B-smooth, then for each prime divisor p of N(a + bα) we find out the ideal ![]() and its multiplicity in the factorization of 〈a + bα〉 as explained above. Since we know a generator of each
and its multiplicity in the factorization of 〈a + bα〉 as explained above. Since we know a generator of each ![]() , we eventually compute a factorization
, we eventually compute a factorization ![]() , where u is a unit in
, where u is a unit in ![]() . What remains is to factor u as a product of elements of
. What remains is to factor u as a product of elements of ![]() . We don’t discuss this step here, but refer the reader to Lenstra et al. [167].
. We don’t discuss this step here, but refer the reader to Lenstra et al. [167].
Sieving
In the QSM, we check the smoothness of a single integer T(c) per trial, whereas for the NFS method we do so for two integers, namely, a + bm and N(a + bα). However, both these integers are much smaller than T(c), and the probability that they are simultaneously smooth is larger than the probability that T(c) alone is smooth. This accounts for the better asymptotic performance of the NFS method compared to the QSM.
One has to check the smoothness of a + bm and N(a + bα) for each coprime a, b in a predetermined interval. This check can be carried out efficiently using sieves. We have to use two sieves, one for filtering out the non-smooth a + bm values and the other for filtering out the non-smooth a + bα values. We should have gcd(a, b) = 1, but computing gcd(a, b) for all values of a and b is rather costly. We may instead use a third sieve to throw away the values of a for a given b for which gcd(a, b) is divisible by primes ≤ B. This still leaves us with some pairs (a, b) for which gcd(a, b) > 1. But this is not a serious problem, since such values are small in number and can be later discarded from the list of pairs (a, b) selected by the smoothness test.
We fix b and allow a to vary in the interval –M ≤ a ≤ M for a predetermined bound M. We use an array ![]() indexed by a. Before the first sieve we initialize this array to
indexed by a. Before the first sieve we initialize this array to ![]() . We may set
. We may set ![]() for those values of a for which gcd(a, b) is known to be > 1 (where +∞ stands for a suitably large positive value). For each small prime p ≤ B and small exponent
for those values of a for which gcd(a, b) is known to be > 1 (where +∞ stands for a suitably large positive value). For each small prime p ≤ B and small exponent ![]() , we compute a′ := –mb (mod ph) and subtract ln p from
, we compute a′ := –mb (mod ph) and subtract ln p from ![]() for each a, –M ≤ a ≤ M, with a ≡ a′ (mod ph). Finally, for each value of a for which
for each a, –M ≤ a ≤ M, with a ≡ a′ (mod ph). Finally, for each value of a for which ![]() is not (close to) 0, that is, for which a + mb is not B-smooth, we set
is not (close to) 0, that is, for which a + mb is not B-smooth, we set ![]() . For the other values of a, we set
. For the other values of a, we set ![]() . One may use incomplete sieving (with a liberal selection criterion) during the first sieve.
. One may use incomplete sieving (with a liberal selection criterion) during the first sieve.
The second sieve proceeds as follows. We continue to work with the value of b fixed before the first sieve and with the array ![]() available from the first sieve. For each prime ideal
available from the first sieve. For each prime ideal ![]() , we compute a″ := –bcp (mod p) and subtract ln p from each location
, we compute a″ := –bcp (mod p) and subtract ln p from each location ![]() for which a ≡ a″ (mod p). For those a for which
for which a ≡ a″ (mod p). For those a for which ![]() ln B for some real ξ ≥ 1, say ξ = 2, we try to factorize a + bα over
ln B for some real ξ ≥ 1, say ξ = 2, we try to factorize a + bα over ![]() and
and ![]() . If the attempt is successful, both a + bm and a + bα are smooth. This second sieve is an incomplete one and, therefore, we must use a liberal selection criterion.
. If the attempt is successful, both a + bm and a + bα are smooth. This second sieve is an incomplete one and, therefore, we must use a liberal selection criterion.
The running time of the SNFSM
For deriving the running time of the SNFSM, take d ≤ (3 ln n/(2 ln ln n))1/3, m = L(n, 2/3, (2/3)1/3), B = L(n, 1/3, (2/3)2/3) and M = L(n, 1/3, (2/3)2/3). From the prime number theorem and from the fact that d is small, it follows that both ![]() and
and ![]() have the same asymptotic bound as B. Also
have the same asymptotic bound as B. Also ![]() meets this bound. We then have L(n, 1/3, (2/3)2/3) unknown quantities on which we have to do Gaussian elimination.
meets this bound. We then have L(n, 1/3, (2/3)2/3) unknown quantities on which we have to do Gaussian elimination.
The integers a + mb have absolute values ≤ L(n, 2/3, (2/3)1/3). If the coefficients of f are small, then
|N(a + bα)| = |bdf(–a/b)| ≤ L(n, 1/3, d · (2/3)2/3) = L(n, 2/3, (2/3)1/3).
Under the heuristic assumption that a + mb and N(a + bα) behave as random integers of magnitude L(n, 2/3, (2/3)1/3), the probability that both these are B-smooth turns out to be L(n, 1/3, –(2/3)2/3), and so trying L(n, 1/3, 2(2/3)2/3) pairs (a, b) is expected to give us L(n, 1/3, (2/3)2/3) relations. The entire sieving process takes time L(n, 1/3, 2(2/3)2/3), whereas solving a sparse system in L(n, 1/3, (2/3)2/3) unknowns can be done essentially in the same time. Thus the running time of the SNFSM is L(n, 1/3, 2(2/3)2/3) = L(n, 1/3, (32/9)1/3).
Exercise Set 4.3
| 4.6 | For | |
| 4.7 | Let k, c, c′, α be positive constants with α < 1. Prove the following assertions.
| |
| 4.8 | Let us assume that an adversary C has computing power to carry out 1012 floating point operations (flops) per second. Let A be an algorithm that computes a certain function P(n) using T(n) flops for an input | |
| 4.9 | Let | |
| 4.10 | Show that the problems IFP and SQRTP are probabilistic polynomial-time equivalent. [H] | |
| 4.11 | In this exercise, we use the notations introduced in connection with the Quadratic Sieve method for factoring integers (Section 4.3.2). We assume that M ≪ H, since
| |
| 4.12 | Reyneri’s cubic sieve method (CSM) Suppose that we want to factor an odd integer n. Suppose also that we know a triple (x, y, z) of integers satisfying x3 ≡ y2z (mod n) with x3 ≠ y2z (as integers). We assume further that |x|, |y|, |z| are all O(pξ) for some ξ, 1/3 < ξ < 1/2.
| |
| 4.13 | Sieve of Eratosthenes Two hundred years before Christ, Eratosthenes proposed a sieve (Algorithm 4.5) for computing all primes between 1 and a positive integer n. Prove the correctness of this algorithm and compute its running time. [H]
Algorithm 4.5. The sieve of Eratosthenes
| |
| 4.14 | This exercise proposes an adaptation of the sieve of Eratosthenes for computing a random prime of a given bit length l. In Section 3.4.2, we have described an algorithm for this computation, that generates random (odd) integers of bit length l and checks the primality of each such integer, until a (probable) prime is found. An alternative strategy is to generate a random l-bit odd integer n and check the integers n, n + 2, n + 4, . . . for primality.
|
