4.8. The Subset Sum Problem

In this section, we assume that be a knapsack set. For , we are required to find out such that , provided that a solution exists. In general, finding such a solution for ∊1, . . . , ∊n is a very difficult problem.[6] However, if the weights satisfy some specific bounds, there exist polynomial-time algorithms for solving the SSP.

[6] In the language of complexity theory, the decision problem of determining whether a solution of the SSP exists is NP-complete.

Let us first define an important quantity associated with a knapsack set:

Definition 4.5.

The density of the knapsack set is defined to be the real number .

If d(A) > 1, then there are, in general, more than one solutions for the SSP (provided that there exists one solution). This makes the corresponding knapsack set A unsuitable for cryptographic purposes. So we consider low densities: that is, the case that d(A) ≤ 1.

There are certain algorithms that reduce in polynomial time the problem of finding a solution of the SSP to that of finding a shortest (non-zero) vector in a lattice. Assuming that such a vector is computable in polynomial time, Lagarias and Odlyzko’s reduction algorithm [157] solves the SSP in polynomial time with high probability, if d(A) ≤ 0.6463. An improved version of the algorithm adapts to densities d(A) ≤ 0.9408 (see Coster et al. [64] and Coster et al. [65]). The reduction algorithm is easy and will be described in Section 4.8.1. However, it is not known how to efficiently compute a shortest non-zero vector in a lattice. The Lenstra–Lenstra–Lovasz (L3) polynomial-time lattice basis reduction algorithm [166] provably finds out a non-zero vector whose length is at most the length of a shortest non-zero vector, multiplied by a power of 2. In practice, however, the L3 algorithm tends to compute a shortest vector quite often. Section 4.8.2 deals with the L3 lattice basis reduction algorithm.

Before providing a treatment on lattices, let us introduce a particular case of the SSP, which is easily (and uniquely) solvable.

Definition 4.6.

A knapsack set {a1, . . . , an} with a1 < ··· < an is said to be superincreasing, if for all j = 2, . . . , n.

Algorithm 4.10 solves the SSP for a superincreasing knapsack set in deterministic polynomial time. The proof for the correctness of this algorithm is easy and left to the reader.

Algorithm 4.10. Solving the superincreasing knapsack problem

Input: A superincreasing knapsack set {a1, . . . , an} with a1 < ··· < an and .

Output: The (unique) solution for of , if it exists, failure, otherwise.

Steps:

for i = n, n – 1, . . . , 1 {
   if (s ≥ ai) { ∊i := 1, s := s – ai. } else { ∊i := 0. }
}
if (s = 0) { Return (∊1, . . . , ∊n). } else { Return “failure”. }

4.8.1. The Low-Density Subset Sum Problem

We start by defining a lattice.

Definition 4.7.

Let n, , d ≤ n, and let be d linearly independent (non-zero) vectors (that is, n-tuples). The lattice L of dimension d spanned by v1, . . . , vd is the set of all -linear combinations of v1, . . . , vd, that is,

We say that v1, . . . , vd constitute a basis of L.

In general, a lattice may have more than one basis. We are interested in bases consisting of short vectors, where the concept of shortness is with respect to the following definition.

Definition 4.8.

Let v := (v1, . . . , vn)t and w := (w1, . . . , wn)t be two n-dimensional vectors in . The inner product of v and w is defined to be the non-negative real number

〈v, w〉 := v1w1 + ··· + vnwn,

and the length of v is defined as

For the time being, let us assume the availability of a lattice oracle which, given a lattice, returns a shortest non-zero vector in the lattice. The possibilities for realizing such an oracle will be discussed in the next section.

Consider the subset sum problem with the knapsack set A := {a1, . . . , an} and let B be an upper bound on the weights (that is, each ai ≤ B). For , we are supposed to find out such that . Let L be the n+1-dimensional lattice in generated by the vectors

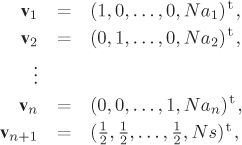
where N is an integer larger than . The vector is in the lattice L, where . Involved calculations (carried out in Coster et al. [64, 65]) show that the probability P of the existence of a vector with ‖w‖ ≤ ‖v‖ satisfies , where c ≈ 1.0628. Now, if the density d(A) of A is less than 1/c ≈ 0.9408, then B = 2c′n for some c′ > c and, therefore, P → 0 as n → ∞. In other words, if d(A) < 0.9408, then, with a high probability, ±v are the shortest non-zero vectors of L. The lattice oracle then returns such a vector from which the solution ∊1, . . . , ∊n can be readily computed.

4.8.2. The Lattice-Basis Reduction Algorithm

Let L be a lattice in specified by a basis of n linearly independent vectors v1, . . . , vn. We now construct a basis of such that (that is, and are orthogonal to each other) for all i, j, i ≠ j. Note that need not be a basis for L. Algorithm 4.11 is known as the Gram–Schmidt orthogonalization procedure.

Algorithm 4.11. Gram–Schmidt orthogonalization

Input: A basis v1, . . . , vn of

Output: The Gram–Schmidt orthogonalization of v1, . . . , vn.

Steps:

.
for i = 2, . . . , n {
   , where .
}

One can easily verify that constitute an orthogonal basis of . Using these notations, we introduce the following important concept:

Definition 4.9.

The basis v1, . . . , vn is called a reduced basis of L, if

Equation 4.16


and

Equation 4.17


A reduced basis v1, . . . , vn of L is termed so, because the vectors vi are somewhat short. More precisely, we have Theorem 4.5, the proof of which is not difficult, but is involved, and is omitted here.

Theorem 4.5.

Let v1, . . . , vn be a reduced basis of a lattice L, and . For any m linearly independent vectors w1, . . . , wm of L, we have

for all i = 1, . . . , m. In particular, for any non-zero vector w of L we have

‖ v1‖2 ≤ 2n–1‖w‖2.

That is, for a reduced basis v1, . . . , vn of L the length of v1 is at most 2(n–1)/2 times that of the shortest non-zero vector in L.

Given an arbitrary basis v1, . . . , vn of a lattice L, the L3 basis reduction algorithm computes a reduced basis of L. The algorithm starts by computing the Gram–Schmidt orthogonalization of v1, . . . , vn. The rational numbers μi,j are also available from this step. We also obtain as byproducts the numbers for i = 1, . . . , n.

Algorithm 4.12 enforces Condition (4.16) |μk,l| ≤ 1/2 for a given pair of indices k and l. The essential work done by this routine is subtracting a suitable multiple of vl from vk and updating the values μk,1, . . . , μk,l accordingly.

Algorithm 4.12. Subroutine for basis reduction

Input: Two indices k and l.

Output: An update of the basis vectors to ensure |μk,l| ≤ 1/2.

Steps:

vk := vk – rvl.

for h = 1, . . . , l – 1 {μk,h := μk,h – rμl,h. }

μk,l := μk,l – r.

If Condition (4.17) is not satisfied by some k, that is, if , then vk and vk–1 are swapped. The necessary changes in the values Vk, Vk–1 and certain μi,j’s should also be incorporated. This is explained in Algorithm 4.13.

Algorithm 4.13. Subroutine for basis reduction

Input: An index k.

Output: An update of the basis vectors to ensure .

Steps:

μ := μk,k–1.   V := Vk + μ2Vk–1.
μk,k–1 := μVk–1/V.   Vk := Vk–1Vk/V.   Vk–1 := V.
Swap (vk, vk–1).
for h = 1, . . . , k – 2 { Swap (μk,h, μk,h–1). }
for h = k + 1, . . . , n {
   μ′ := μh,k–1 – μμh,k.   μh,k–1 := μh,k + μk,k–1μ′.   μh,k := μ′.
}

The main basis reduction algorithm is described in Algorithm 4.14. It is not obvious that this algorithm should terminate at all. Consider the quantity D := d1 · · · dn–1, where di := | det(〈vk, vl〉)1≤k,l≤i| for each i = 1, . . . , n. At the beginning of the basis reduction procedure one has di ≤ Bi for all i = 1, . . . , n, where B := max(|vi|2 | 1 ≤ i ≤ n). It can be shown that an invocation of Algorithm 4.12 does not alter the value of D, whereas interchanging vi and vi–1 in Algorithm 4.13 decreases D by a factor < 3/4. It can also be shown that for any basis of L the value D is bounded from below by a constant which depends only on the lattice. Thus, Algorithm 4.14 stops after finitely many steps.

Algorithm 4.14. Basis reduction in a lattice

Input: A basis v1, . . . , vn of a lattice L.

Output: v1, . . . , vn converted to a reduced basis.

Steps:

Compute the Gram–Schmidt orthogonalization of v1, . . . , vn (Algorithm 4.11).

/* The initial values of μi,j and Vi are available at this point */
i := 2.
while (i < n) {
   if (|μi,i–1| > 1/2) { Call Algorithm 4.12 with k = i and l = i – 1. }
   if 
      Call Algorithm 4.13 with k = i.
      i := max(2, i – 1).
   }
   for j = i – 2, i – 3, . . . , 1 {
      if (|μi,j| > 1/2) { Call Algorithm 4.12 with k = i and l = j. }
   }
   i++.
}

For a more complete treatment of the L3 basis reduction algorithm, we refer the reader to Lenstra et al. [166] (or Mignotte [203]). It is important to note here that the L3 basis reduction algorithm is at the heart of the Lenstra–Lenstra–Lovasz algorithm for factoring a polynomial in . This factoring algorithm indeed runs in time polynomially bounded by the degree of the polynomial to be factored and is one of the major breakthroughs in the history of symbolic computing.

Exercise Set 4.8

4.27Let be a knapsack set. Show that:

  1. If A is superincreasing with a1 < ··· < an, then ai ≥ 2i–1 for all i = 1, . . . , n and hence .

  2. If , then there exist two different tuples (∊1, . . . , ∊n) and in {0, 1}n such that .

4.28Let L be a lattice in and let v1, . . . , vn constitute a basis of L. The determinant of L is defined by

det L := det(v1, . . . , vn).

  1. Show that det L is an invariant of the lattice L (that is, independent of the basis v1, . . . , vn of L).

    Let be the Gram–Schmidt orthogonalization of the basis v1, . . . , vn.

  2. Show that det .

  3. Prove the Hadamard inequality: det L ≤ ‖v1‖ · · · ‖vn‖.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.
Reset
18.116.19.75