8.4. Quantum Cryptanalysis

The quantum parallelism has been effectively exploited to design fast (polynomial-time) algorithms to solve some of the intractable mathematical problems discussed in Chapter 4. With the availability of quantum computers, cryptographic systems that derive their security from the intractability of these problems will be unusable (completely insecure). Nobody, however, has the proof that these intractable problems cannot have fast classical algorithms. It is interesting to wait and see which (if any) is invented first, a quantum computer or a polynomial-time classical algorithm.

Let us set up some terminology for the rest of this chapter. Let P be a unitary operator on a qubit. One can apply P individually on the i-th bit of an n-bit register. In this case, we denote the operation by P_i. If P_i is operated for each i = 1, . . . , n (in succession or simultaneously), then we abbreviate P₁ · · · P_n by the short-hand notation P⁽ⁿ⁾. The parentheses distinguish the operation from Pⁿ which is the n-fold application of P on a single qubit.

If P and Q are unitary transforms on n₁- and n₂-bit quantum registers respectively, we let P ⊗ Q denote the unitary transform on an n₁ + n₂-bit register, with P operating on the left n₁ bits and Q on the right n₂ bits of the register.

8.4.1. Shor’s Algorithm for Computing Period

Let N := 2ⁿ for some . Let be a periodic function with (least) period r, that is, f(x + kr) = f(x) for every x, . Suppose further that 1 ≪ r ≤ 2^n/2 and also that f(0), f(1), . . . , f(r – 1) are pairwise distinct. Shor proposed an algorithm for an efficient computation of the period r in this case.

Let’s first look at the problem classically. If one evaluates f at randomly chosen points, by the birthday paradox (Exercise 2.172) one requires evaluations of f on an average in order to find two different integers x and y with f(x) = f(y). But then r|(x – y). If sufficiently many such pairs (x, y) are available, the period can be obtained by computing the gcd of the integers x – y. If r is large, say, r = O(2^n/2), this gives us an algorithm for computing r in expected time exponential in n. Shor’s quantum algorithm determines r in expected time polynomial in n.

Let us assume that we have an oracle U_f which, on input the 2n-bit value |x〉_n|y〉_n, computes |x〉_n|f(x) ⊕ y〉_n. We prepare a 2n-bit register A in the state |0〉_n|0〉_n. Then, we apply the Hadamard transform H⁽ⁿ⁾ on the left n-bits. By Exercise 8.8, the state of A becomes

Supplying this state as the input to the oracle U_f yields the state

We then measure the output register (right n bits). By the generalized Born rule, we get a value for some and the state of the register A collapses to the uniform superposition of all those |x〉|f(x)〉 for which f(x) = f(x₀). By the given periodicity properties of f, the post-measurement state of the input register (left n bits) can be written as

Equation 8.1

for some M determined by the relations:

x₀ + (M – 1)r < N ≤ x₀ +Mr.

This is an interesting state, for if we were allowed to make copies of this state and measure the different copies, we could collect some values x₀+j₁r, . . . , x₀+j_kr, which in turn would reveal r with high probability. But the no-cloning theorem disallows making copies of quantum states. Shor proposed a trick to work around with this difficulty. He considered the following transform:

Equation 8.2

By Exercise 8.13, F is a unitary transform. F is known as the Fourier transform. Applying F to State (8.1) transforms the input register to the state

A measurement of this state gives an integer with the probability

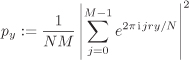
Application of the Fourier transform to State (8.1) helps us to concentrate the probabilities of measurement outcomes in strategic states. More precisely, consider a value of y, where –1/2 ≤ ∊_k < 1/2, that is, a value of y close to an integral multiple of N/r. In this case,

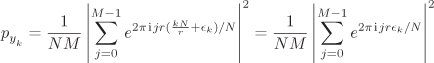
The last summation is that of a geometric series and we have

Now, we use the inequalities for 0 ≤ x ≤ π/2 and the facts that rM ≈ N and that to get

Since has about r positive integral multiples less than N and each such multiple has a closest integer y_k for some k, the probability that we obtain one such y_k as the outcome of the measurement is at least 4/π² = 0.40528 . . . , that is, after O(1) iterations of the above procedure we get some y_k. The Fourier transform increases the likelihood of getting some y_k to a level bounded below by a positive constant.

What remains is to show that r can be retrieved from such a useful observation y_k. We have . If a/b and c/d are two distinct rationals with b, and with and , then by the triangle inequality we have . On the other hand, since a/b ≠ c/d, we have , a contradiction. Therefore, since , there is a unique rational k/r satisfying , and this rational k/r can be determined by efficient classical algorithms, for example, using the continued fraction expansion^[2] of y_k/N.

^[2] Consult Zuckerman et al. [316] to learn about continued fractions and their applications in approximating real numbers.

If gcd(k, r) = 1, we get r. We can verify this by checking if f(x) = f(x + r). If gcd(k, r) > 1, we get a factor of r. Repeating the entire procedure gives another k′/r, from which we get (hopefully) another factor of r (if not r itself). After a few (O(1)) iterations, we obtain r as the lcm of its factors obtained.

Much of the quantum magic is obtained by the use of the Fourier transform F on a suitably prepared quantum register. The question is then how easy it is to implement F. We will not go to the details, but only mention that a circuit consisting of basic quantum gates and of size O(n²) can be used to realize the Fourier transform (cf. Exercise 8.14).

To sum up, we have a polynomial-time (in n) randomized quantum algorithm for computing the period r of f. This leads to efficient quantum algorithms for solving many classically intractable problems of cryptographic significance.

8.4.2. Breaking RSA

Let m = pq with p, . We have φ(m) = (p – 1)(q – 1). Choose an RSA key pair (e, d) with gcd(e, φ(m)) = 1 and ed ≡ 1 (mod φ(m)). Given a message the ciphertext message is b ≡ a^e (mod m). The task of a cryptanalyst is to compute a from the knowledge of m, e and b. If gcd(b, m) > 1, then this gcd is a non-trivial factor of m. So assume that . But then also. Since b ≡ a^e (mod m), b is in the subgroup of generated by a. Similarly, a ≡ b^d (mod m), that is, a is in the subgroup of generated by b. It follows that these two subgroups are equal and, in particular, the multiplicative orders of a and b modulo m are the same. This order—call it r—divides φ(m) and hence is ≤ (p – 1)(q – 1) < m.

Choose with N := 2ⁿ ≥ m² > r². The function sending x ↦ b^x (mod m) is periodic of (least) period r. By Shor’s algorithm, one computes r efficiently. Since gcd(e, φ(m)) = 1 and r|φ(m), we have gcd(e, r) = 1, that is, using the extended gcd algorithm one obtains an integer d′ with d′e ≡ 1 (mod r). But then b^d′ ≡ a^d′e ≡ a (mod m).

The private key d is the inverse of e modulo φ(m). It is not necessary to compute d for decrypting b. The inverse d′ of e modulo r = ord_m(a) = ord_m(b) suffices.

8.4.3. Factoring Integers

Let m be a composite integer that we want to factor. Choose a non-zero integer . If gcd(a, m) > 1, then we already know a non-trivial factor of m. So assume that gcd(a, m) = 1, that is, . Let r := ord_m(a).

As in the case of breaking RSA, choose with N := 2ⁿ ≥ m² > r². The function , x ↦ a^x (mod m), is periodic of least period r. Shor’s algorithm computes r. If r is even, we can write:

(a^r/2 – 1)(a^r/2 + 1) ≡ 0 (mod m).

Since ord_m(a) = r, a^r/2 – 1 ≢ 0 (mod m). If we also have a^r/2 + 1 ≢ 0 (mod m), then gcd(a^r/2 + 1, m) is a non-trivial factor of m. It can be shown that the probability of finding an even r with a^r/2 + 1 ≢ 0 (mod m) is at least half (cf. Exercise 4.9). Thus, trying a few integers one can factor m.

8.4.4. Computing Discrete Logarithms

A variant of Shor’s algorithm in Section 8.4.1 can be used to compute discrete logarithms in the finite field , , . For the sake of simplicity, let us concentrate only on prime fields (s = 1). Let g be a generator of and our task is to compute for a given an integer with a ≡ g^r (mod p). We assume that p is a large prime, that is, p is odd.

Choose with N := 2ⁿ satisfying p < N < 2p. We use a 3n-bit quantum register A in which the left 2n bits constitute the input part and the right n bits the output part. The input part is initialized to the uniform superposition of all pairs , that is, A has the initial state:

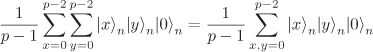
(see Exercise 8.15). Then, we use an oracle

U_f : |x〉_n|y〉_n|z〉_n ↦ |x〉_n|y〉_n|f(x, y) ⊕ z〉_n

to compute the function f(x, y) := g^xa^–y (mod p) in the output register. Applying U_f transforms A to the state

Measurement of the output register now gives a value z ≡ g^k (mod p) for some and causes the input register to jump to the state

Note that g^xa^–y ≡ g^k (mod p) if and only if x – ry ≡ k (mod p – 1), that is, only those pairs (x, y) that satisfy this congruence contribute to the post-measurement state. For each value of y modulo p – 1, we get a unique x ≡ ry + k (mod p – 1), that is, there are exactly p – 1 such pairs (x, y).

If we were allowed make copies of this state and observe two copies separately, we would get pairs (x₁, y₁) and (x₂, y₂) with x₁ – ry₁ ≡ x₂ – ry₂ ≡ k (mod p – 1). Now, if gcd(y₁ – y₂, p – 1) = 1, we would get r ≡ (y₁ – y₂)^–1 (x₁ – x₂) (mod p – 1). But we are not allowed to copy quantum states. So Shor used his old trick, that is, applied the Fourier transforms

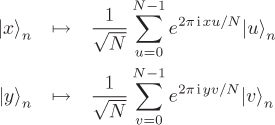
to obtain the state

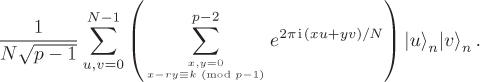
A measurement of the input register at this state yields with probability:

Equation 8.3

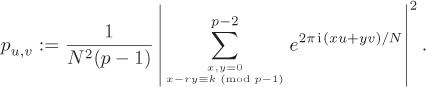
As in Shor’s period-finding algorithm, we now require to identify a set of useful pairs (u, v) which are sufficiently many in number so as to make the probability of observing one of them bounded below by a positive constant. We also need to demonstrate how a useful pair can reveal the unknown discrete logarithm r of a. The jugglery with inequalities and approximations is much more involved in this case. Let us still make a patient attempt to see the end of the story.

First, we eliminate one of x, y from Equation (8.3). Since x ≡ ry + k (mod p – 1) and 0 ≤ x ≤ p – 2, we have x = (ry + k) rem . But then . Let j be the integer closest to u(p – 1)/N, that is, u(p – 1) = jN + ∊ with , –N/2 < ∊ ≤ N/2. This yields

Equation 8.4

where

Equation 8.5

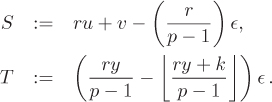
Since is an integer, substituting Equation (8.4) in Equation (8.3) gives

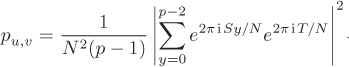
Writing S = lN + σ with –N/2 < σ ≤ N/2 then gives

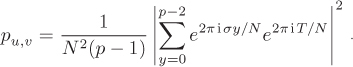
We now impose the usefulness conditions on u, v:

Equation 8.6

Equation 8.7

Involved calculations show that the probability p_u,v for a (u, v) satisfying these two conditions is at least . Let us now see how many pairs (u, v) satisfy the conditions. From Equation (8.5), it follows that for each u there exists a unique v, such that Condition (8.6) is satisfied. Condition (8.7), on the other hand, involves only u. If w := v₂(p – 1), then 2^w must divide ∊. For each multiple of 2^w not exceeding N/12 in absolute value, we get 2^w distinct solutions for u modulo N. (We are solving for u the congruence u(p – 1) ≡ ∊ (mod 2ⁿ).) There is a total of at least N/12 of them. Therefore, the probability of making any one of the useful observations (u, v) is at least , since N < 2p.

We finally explain the extraction of r from a useful observation (u, v). Condition (8.6) and Equation (8.5) give . Dividing throughout by N and using the fact that u(p – 1) = jN + ∊, we get

that is, the fractional part of must lie between and . The measurement of the input gives us v and we know N. We approximate to the nearest multiple of and get rj ≡ λ (mod p – 1). Now, j, being the integer closest to u(p – 1)/N, is also known to us. If gcd(j, p – 1) = 1, we have r ≡ j^–1λ (mod p – 1). We don’t go into the details of determining the likelihood of the invertibility of j modulo p – 1. A careful analysis shows that Shor’s quantum discrete-log algorithm runs in probabilistic polynomial time (in n).

Exercise Set 8.4

8.13	Let F be the Fourier Transform (8.2). For basis vectors |x〉 and |x′〉, show that Conclude that F is a unitary transform.
8.14	Let N = 2n. Let x, have binary expansions (xn–1 · · · x1x0)2 and (yn–1 · · · y1y0)2 respectively. Show that xy/N equals an integer plus the quantity yn–1 (.x0) + yn–2(.x1x0) + yn–3(.x2x1x0) + · · · + y0(.xn–1 xn–2 . . . x0), where . Deduce that the quantum Fourier Transform (8.2) can be written as where the i-th expression in parentheses applies to the i-th bit from the left.
8.15	Let , N := 2n and . Consider an (n + 1)-bit quantum register with input consisting of the left n bits and the output the rightmost bit. Suppose there is an oracle Uf that takes an n-bit input x and outputs the bit: First prepare the register in the state . Then, apply Uf on this register and finally measure the output bit. Describe the state of the input register after this measurement depending on the outcome of the measurement.
8.16	Recall that the Fourier Transform (8.2) is defined for N equal to a power of 2. It turns out that for such values of N the quantum Fourier transform is easy to implement. For this exercise, assume hypothetically that one can efficiently implement F for other values of N too. In particular, take N = p – 1 in Shor’s quantum discrete-log algorithm. Show that in this case, the probability pu,v of Equation (8.3) becomes: [View full size image] Conclude that an outcome (u, v) of measuring the input register yields r ≡ –u–1v (mod p – 1), provided gcd(u, p – 1) = 1.