10
Lock and Wait-Free Communication
CONTENTS
10.1 Basic Principles and Definitions
From the previous chapters, Chapter 5 in particular, we know that a shared object, or concurrent object, is a data structure that can be accessed and modified by means of a fixed, predefined set of operations by a number of concurrent processes. Uncontrolled, concurrent access to a shared object may lead to the unrecoverable corruption of the object contents, a dangerous situation known as race condition.
For this reason, object access is traditionally implemented by means of critical sections or regions. A mutual exclusion mechanism, for example, a semaphore, governs the access to critical regions and makes processes wait if necessary. In this way, it ensures than only one process at a time is allowed to access and/or modify the object. With this approach, usually called lock-based object sharing, a process wishing to access a shared object must obey the following protocol:
Acquire a lock of some sort before entering the critical region;
Access the shared object within the critical region;
Release the lock when exiting the critical region.
As long as a process holds a lock, any other process contending for the same lock is enforced to wait—in other words it is blocked—until the first one exits from its critical region. As a side effect, if the process holding the lock is delayed (or halted due to an error), the other processes will be unable to progress, possibly forever. Even without working out all the details, it is easy to imagine that lock-based object sharing among processes with different priorities is an important issue in a real-time system.
In fact, when objects are shared in this way, a higher-priority process may be forced to wait for a lower-priority one and, in a sense, this scenario goes against the very concept of priority. Even if adequate methods to deal with the problem exist, and will be discussed in Chapter 15, it is also true that some hardware and software components introduce execution delays that are inherently hard to predict precisely, for example,
Page faults (on demand-paging systems)
Cache and TLB misses
Branch mispredictions
Failures
This implies a certain degree of uncertainty on how much time a given task will actually spend within a critical region in the worst case, and the uncertainty is reflected back into worst-case blocking time computation, as we will see in Chapter 15.
Even if a full discussion of the topic is beyond the scope of this book, this chapter contains a short introduction to a different method of object sharing, known as lock and wait-free communication. The main difference with respect to lock-based object sharing is that the former is able to guarantee the consistency of an object shared by many concurrent processes without ever forcing any process to wait for another.
In particular, we will first look at a very specific method, namely, a lock-free algorithm for sharing data among multiple, concurrent readers and one single writer. Then, another method will be presented, which solves the problem in more general terms and allows objects of any kind to be shared in a lock-free way. The two methods are related because some aspects of the former—namely, the properties of multidigit counters—are used as a base for the latter.
The inner workings of this kind of algorithms are considerably more complex than, for instance, semaphores. Hence, this chapter is, by necessity, based on more formal grounds than the previous ones and includes many theorems. However, the proof of most theorems can safely be skipped without losing the general idea behind them.
See, for example, References [4, 3] for a more thorough discussion about how lock-free objects can be profitably adopted in a real-time system, as well as a framework for their implementation.
10.1 Basic Principles and Definitions
Definition 10.1. Given a system of processes J = {J1, ..., Jn} wishing to access a shared object S, the implementation of S is lock-free (sometimes called nonblocking) if
some process Ji ∈ J must complete an operation on S after the system J takes a finite number of steps.
In this definition, a step is meant to be an elementary execution step of a process such as, for example, the execution of one machine instruction. The concept of execution step is not tightly related to time, but it is assumed that each execution step requires a finite amount of time to be accomplished. In other words, the definition guarantees that, in a finite amount of time, some process Ji—not necessarily all of them—will always make progress regardless of arbitrary delays or halting failures of other processes in J.
It is easy to show, by means of a counterexample, that sharing an object by introducing critical regions leads to an implementation that is necessarily not lock-free. That is, let us consider a shared object accessed by a set of processes J = {J1 ,..., Jn} and let us assume that each process contains a critical section, all protected by the same lock.
If any process Ji acquires the lock, enters the critical section, and halts without releasing the lock, regardless of what steps the system J takes and the number of such steps, none of the processes will complete its operation. On the contrary, all processes will wait forever to acquire the lock, without making progress, as soon as they try to enter the critical section.
Definition 10.2. Similarly, given a set of processes J = {J1 ,..., Jn} wishing to access a shared object S, the implementation of S is wait-free if
each process Ji ∈ J must complete an operation after taking a finite number of steps, provided it is not halted.
The definition guarantees that all nonhalted processes—not just some of them as stated in the definition of lock-free—will make progress, regardless of the execution speed of other processes. For this reason, the wait-free condition is strictly stronger than the lock-free condition.
Both lock-free and wait-free objects have a lot of interesting and useful properties. First of all, lock-free and wait-free objects are not (and cannot be) based on critical sections and locks. Lock-free objects are typically implemented using retry loops in which a process repeatedly tries to operate on the shared object until it succeeds. Those retry loops are potentially unbounded and may give rise to starvation for some processes.
On the other hand, wait-freedom precludes all waiting dependencies among processes, including potentially unbounded loops. Individual wait-free operations are therefore necessarily starvation-free, another important property in a real-time system.
10.2 Multidigit Registers
One of the first widely known, lock-free algorithm was a concurrent read/write buffer for multiple readers and one single writer, proposed by Lamport in 1977 [56]. Its basic principle is that, if a multidigit register is read in one direction while it is being written in the opposite direction, the value obtained by the read has a few useful properties.
Even if it is not so commonly used in practice, this algorithm has the advantage of being relatively simple to describe. Nevertheless, it has a great teaching value because it still contains all the typical elements to be found in more complex lock-free algorithms. This is the main reason it will be presented here. It should also be noted that simple nonblocking buffers for real-time systems were investigated even earlier by Sorenson and Hemacher in 1975 [84].
The main underlying hypothesis of the Lamport’s method is that there are basic units of data, called digits, which can be read and written by means of indivisible, atomic operations. In other words, it is assumed that the underlying hardware automatically sequences concurrent operations at the level of a single digit. This hypothesis is not overly restrictive because digits can be made as small as needed, even as small as a single bit. For example, making them the size of a machine word is enough to accommodate most existing hardware architectures, including many shared-memory multiprocessor systems.
Let v denote a data item composed of one or more digits. It is assumed that two distinct processes cannot concurrently modify v because there is only one writer. Since the value of v may, and usually will, change over time, let v[0] denote the initial value of v. This value is assumed to be already there even before the first read operation starts. In other words, it is assumed that the initial value of v is implicitly written by an operation that precedes all subsequent read operations. In the same way, let v[1], v[2],..., denote the successive values of v over time.
Due to the definition just given, each write operation to v begins with v equal to v[i], for some i ≥ 0, and ends with v equal to v[i+1]. Since v is in general composed of more than one digit, the transition from the old to the new value cannot be accomplished in one single, atomic step.
The notation v = v1, ... ,vm indicates that the data item v is composed of the subordinate data items vj, 1 ≤ j ≤ m. Each subordinate data item vj is only written as part of a write to v, that is, subordinate data items do not change value “on their own.” For simplicity, it is also assumed that a read (or write) operation of v involves reading (or writing) each vj. If this is not the case, we pretend that a number of dummy read (or write) operations occur anyway. For write operations, if a write to v does not involve writing vj, we pretend that a write to vj was performed, with a value that happens to be the same as that subordinate data item had before. Under these hypotheses, we can write
In particular, we can say that the i-th value v assumes over time, v[i], is composed by the i-th value of all its subordinate data items , 1 ≤ j ≤ m.
When one ore more processes read a data item that cannot be accessed in an atomic way, while another process is updating it, the results they get may be difficult to predict. As shown in Figure 10.1, the most favorable case happens when a read operation is completely performed while no write operation is in progress. In this case, it will return a well-defined value, that is, one of the values v[i] the data item v assumes over time. For example, the leftmost read operation shown in the figure will obtain v[2].
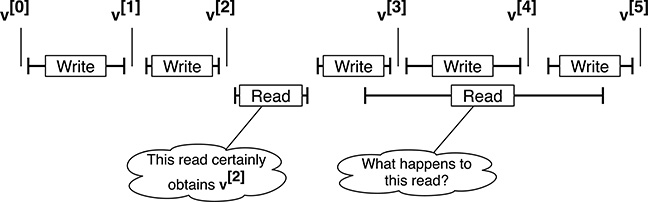
FIGURE 10.1
When one ore more processes read a data item that cannot be accessed in an atomic way while another process is updating it, the results they get may be difficult to predict.
However, a read of v that is performed concurrently and that overlaps with one or more writes to v may obtain a value different from any v[i]. In fact, if v is not composed of a single digit, reading and writing it involves a sequence of separate operations that take a certain amount of time to be performed. All those individual operations, invoked by different processes, are executed concurrently and may therefore overlap with each other.
By intuition, a read operation performed concurrently with one or more write operations will obtain a value that may contain “traces” of different values v[i]. If a read obtains traces of m different values, that is, v[i1],..., v[im], we say that it obtained a value of v[k,l], where k = min(i1,...,im) and l = max(i1,...,im). According to how k and l are defined, it must be 0 ≤ k ≤ l.
Going back to Figure 10.1, we may be convinced that the rightmost read operation may return traces of v[2], v[3], v[4], and v[5] because the time frame occupied by the read operation spans across all those successive values of v. More specifically, the read operation started before v[2] was completely overwritten by the new value, made progress while values v[3], v[4], and v[5] were being written into v, but ended before the write operation pertaining to v[6] started.
It should also be remarked that lock-based techniques must not be concerned with this problem because they enforce mutual exclusion between read and write operations. For instance, when using a mutual exclusion semaphore to access v, the scenario shown in the rightmost part of Figure 10.1 simply cannot happen because, assuming that the semaphore has a First Come First Served (FCFS) waiting queue,
the read operation will start only after the write operation of v[3] has been fully completed; and
the next write operation of v[4] will be postponed until the read operation has read all digits of v.
More formally, let v be a sequence of m digits: v = d1 ,..., dm. Since reading and writing a single digit are atomic operations, a read obtains a value . But since is a digit of value v[ij], we can also say that the read obtained a trace of that particular value of v. In summary, the read obtains a value v[k,l], where k = min(i1,...,im) and l = max(i1,...,im). Hence, the consistency of this value depends on how k and l are related:
If k = l, then the read definitely obtained a consistent value of v, and the value is .
If k ≠ l, then the consistency of the value obtained by the read cannot be guaranteed.
The last statement does not mean that if k ≠ l the read will never get a consistent value. A consistent value can still be obtained if some digits of v were not changed when going from one value to another. For instance, a read of a 3-digit data item v may obtain the value
because it has been performed while a write operation was bringing the value of v from v[6] to v[7]. However, if the second digit of v is the same in both v[6] and v[7], this still is a consistent value, namely, v[6].
In general, a data item v can be much more complicated than a fixed sequence of m digits. The data item size may change with time so that successive values of v may consist of different sets of digits. This happens, for instance, when v is a list linked with pointers in which a certain set of digits may or may no longer be part of the data item’s value, depending on how the pointers are manipulated over time.
In this case, a read operation carried out while v is being updated may return digits that were never part of v. Moreover, it may even be hard to define what it means for a read to obtain traces of a certain value v[i]. Fortunately, to solve the readers/writer problem for v, it turns out that the important thing to ensure is that a read does not return traces of certain versions of v.
More formally, we only need a necessary (not sufficient) condition for a read to obtain traces of a certain value v[i]. Clearly, if this condition does not hold, the read cannot obtain traces of v[i]. By generalizing what was shown in the example of Figure 10.1, the necessary conditions can be stated as follows:
Lemma 10.1. If a read of v obtains traces of value v[i], then
the beginning of the read preceded the end of the write of v[i+1]; and
the end of the read followed the beginning of the write of v[i].
It is easy to prove that this theorem is true in the special case of a multidigit data item. It is also a reasonable assumption in general, for other types of data, although it will be harder to prove it.
Proof. For a multidigit number, the theorem can be proven by showing that if either necessary condition is false, then a read of v cannot obtain a trace of v[i]. In particular:
Immediately after the write of v[i+1] concludes, it is , because all digits of v have been updated with the new value they have in v[i+1].
If the beginning of the read follows the end of this write, the read obtains a value with ij ≥ i + 1, that is, ij > i for 1 ≤ j ≤ m. Informally, speaking, it may be either ij = i + 1 if the read got the k-th digit before any further update was performed on it by the writer, or ij > i + 1 if the digit was updated with an even newer value before the read.
In any case, it cannot be ij < i + 1 for any j because, as stated before, all digits pertaining to v[i], as well as any earlier value, were overwritten before the read started. Hence, the read cannot obtain traces of v[i].
Immediately before the beginning of the write of v[i], it is , because none of its digits have been updated yet.
If the end of the read precedes the beginning of this write, the read obtains a value with ij ≤ i − 1, that is, ij < i for 1 ≤ j ≤ m. Informally speaking, for any j, it will either be ij = i − 1, meaning that the read received the latest value of the j-th digit, or ij < i − 1, signifying it received some past value.
As in the previous case, since the read operation cannot “look into the future,” the read cannot obtain traces of v[i] because it cannot be ij ≥ i for any j.
The necessary condition just stated can be combined with the definition of v[k,l], given previously, to extend it and make it more general. As before, the following statement can be proven for multidigit data items, whereas it is a reasonable assumption, for other types of data:
Lemma 10.2. If a read of v obtains traces of version v[k,l], then
the beginning of the read preceded the end of the write of v[k+1]; and
the end of the read followed the beginning of the write of v[l].
It is now time to discuss a few useful properties of the value a read operation can obtain when it is performed on a multidigit data item concurrently with other read operations and one single write operation. In order to this, it is necessary to formally define the order in which the groups of digit forming a multidigit data item are read and written.
Let v = v1 ,..., vm, where the vj are not necessarily single digits but may be groups of several adjacent digits. A read (or write) of v is performed from left to right if, for each 1 ≤ j < m, the read (or write) of vj is completed before the read (or write) of vj+1 is started. Symmetrically, a read (or write) of v is performed from right to left if, for each 1 < j ≤ m, the read (or write) of vj is completed before the read (or write) of vj−1 is started.
Before continuing, it should be noted that there is no particular reason to state that lower-numbered digit groups are “on the left” of the data item, and that higher-numbered digit groups are “on the right.” This definition is needed only to give an intuitive name to those two read/write orders and be able to tell them apart. An alternative statement that would place higher-numbered digit groups on the left would clearly be equally acceptable.
It is also important to remark that the order in which the individual digits, within a certain digit group vj are read (or written) is left unspecified by the definitions.
Theorem 10.1. Let v = v1 ,..., vm and assume that v is always written from right to left. A read performed from left to right obtains a value in which the kj and lj satisfy the following inequality:
Proof. By the definition of kj and lj, we already know that kj ≤ lj for each 1 ≤ j ≤ m. It is only necessary to prove that lj ≤ kj+1 for each 1 ≤ j < m.
To do this, we will prove that the actions performed by the read operation being considered and a concurrent write operation must happen in a certain order. In turn, all those actions can overlap with other read operations, but there is no need to consider them because any action one reader performs cannot modify the value of the data item being accessed, and therefore cannot influence the value that another reader obtains in the meantime.
Namely, we will consider the following sequence of 5 actions, and prove that they must necessarily occur in the given order, as follows:
End writing
Begin writing
End reading
Begin reading
End writing
Proving that action 1 precedes 2 is easy because the write operation is performed from right to left and sequentially. Hence, the write operation begins writing the next group of digits (the j-th group) only after finishing with the previous one (the j + 1-th).
Since the read of returned a trace of , the end of the read followed the beginning of the write of , from the second part of Lemma 10.2. Therefore, action 2 precedes 3.
As with the write operation, the read operation is also performed sequentially, but from left to right. Hence, the read operation involving the j + 1-th group of digits begins after the j-th group has been read completely. As a consequence, action 3 precedes 4.
Since the read of returned a trace of , the beginning of the read preceded the end of the write of , from the first part of Lemma 10.2. Hence, action 4 precedes 5.
In summary, we have just proved that writing of (action 1) ends before the writing of (action 5) starts. Since both actions are performed by a single writer, because there is only one writer in the system and version numbers are monotonically increasing integer values, it must be lj < kj + 1 + 1, that is, lj ≤ kj+1. The proof does not make any assumption of j, and hence, it is valid for any 1 ≤ j < m.
It should be noted that a “mirror image” of this theorem, as it is called in Reference [56], also holds, in which the read/write order, as well as the inequalities, are reversed. It can be proven in exactly the same way.
So far, digits have been defined as basic units of data, but no hypotheses have been made about what individual digits contain or mean. More interesting properties can be derived if it is assumed that digits actually hold an integer value—as in ordinary digits and numbers—but a few more definitions are needed to proceed.
Let, as usual, v = d1 ,..., dm, where dj are digits. If all the digits happen to be integers, we say that v is an m-digit number. The operator μ(v) gives the m − 1 leftmost digits of v, that is,
In the special case m = 1, μ(v) is defined to be zero. The definition of μ(·) is useful for giving an inductive definition of the usual “less than” relation < on m-digit numbers, as follows:
Definition 10.3. Let v = d1 ,..., dm and w = e1 ,..., em be two m-digit numbers. It is v < w if and only if
μ(v) < μ(w), or
μ(v) = μ(w) and dm < em.
According to this definition, the leftmost digit (d1) is considered to be the most significant one. As for the definition of read and write orders, there is nothing special about this choice.
From now on, the symbol < will be overloaded to denote two distinct “less than” relations on different domains:
On integers, possibly held in a digit, as in dm < em
On m-digit numbers, as in v < w
In order to reason about the numeric value obtained by read operations on an m-digit number, we start by proving this preliminary Lemma:
Lemma 10.3. Let v = d1 ,..., dm be an m-digit number, and assume that i ≤ j implies v[i] ≤ v[j], that is, successive write operations never decrease its numeric value. The following propositions hold:
Proof. The proof is carried out by induction on m—the number of digits of v—starting from the base case m = 1. When m = 1, v is a single-digit number, that is, v = d1. From the hypothesis,
Then,
But , by definition, and hence,
But (10.7) is equivalent to the first proposition of the Lemma. The second proposition can be derived in a similar way by observing that
Hence, it must be
For the induction step, we assume that m > 1 and that the Lemma is true for m − 1; this will be our induction hypothesis. By definition of μ(·), according to Definition 10.3, v[i] ≤ v[j] implies that μ(v[i]) ≤ μ(v[j]). We can therefore apply the induction hypothesis because its premises are satisfied. From the induction hypothesis,
The inequality on the right of (10.10) still holds if we append the same digit to both its sides:
From the hypotheses, it is also known that km ≤ k, and this implies v[km] ≤ v[k]. In summary, we have
but this is exactly what the first proposition of the Lemma states. The second proposition can be proven in the same way, basically by reversing all inequalities in the proof.
Theorem 10.2. Let v = d1 ,..., dm be an m-digit number, and assume that i ≤ j implies v[i] ≤ v[j] as in Lemma 10.3. The following propositions hold:
If v is always written from right to left, then a read from left to right obtains a value v[k,l] ≤ v[l].
If v is always written from left to right, then a read from right to left obtains a value v[k,l] ≥ v[k].
Proof. Since the dj are single digits and read/write operations on them are assumed to be atomic, reading a digit always returns a value in which kj = lj for all 1 ≤ j ≤ m. Let be that value.
From Theorem 10.1, we know that if v is written from right to left and read from left to right, the value obtained by the read is
Since l = max(k1,..., km) by definition, it certainly is
and we can apply the first proposition of Lemma 10.3 to state that
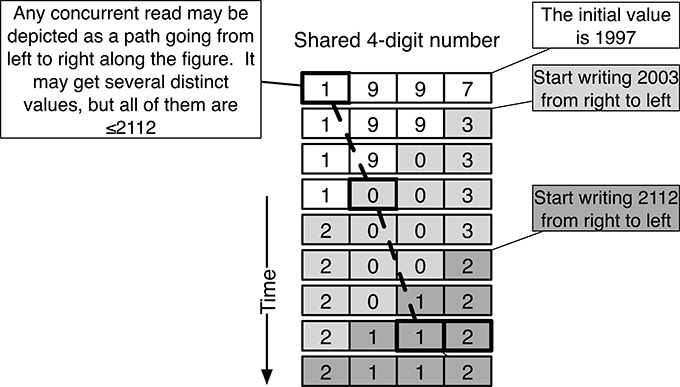
FIGURE 10.2
An example of how concurrent read and write operations, performed in opposite orders, relate to each other.
The last equation proves the first proposition of the Theorem. The second proposition can be proved in a similar way using the “mirror image” of Theorem 10.1 and the second proposition of Lemma 10.3.
An informal but perhaps more intuitive way of phrasing Theorem 10.2 is as follows. If there is a writer that repeatedly updates an m-digit number, bringing it from v[k] to v[l] without ever decreasing its value, any read operation performed concurrently may return an inconsistent value v[k,l], with k < l.
However, if the write operation proceeds from right to left (that is, from the least significant digit to the most significant one) and the read operation is performed from left to right, the value obtained by the read operation will not be completely unpredictable. Rather, it will be less than or equal to v[l], the most recent value the read operation got a trace of.
Symmetrically, if the write operation proceeds from left to right and the read operation is performed from right to left, the value will be greater than or equal to v[k], the oldest value the read operation got a trace of.
Figure 10.2 illustrates, with an example, how concurrent read and write operations, performed in opposite orders, relate to each other. The figure shows a shared, 4-digit number with an initial value of 1997. Two sequential write operations, shown on the right part of the figure, increment it to 2003 at first and then to 2112, from right to left. The central part of the figure lists all the values assumed by the 4-digit number during the updates. Digit values pertaining to distinct write operations are shown with distinct shades of grey in the background, whereas the initial values have a white background.
With this depiction, a read operation performed concurrently with the write operations mentioned above is represented by a path going from left to right along the figure and picking one value for each digit. Figure 10.2 shows one of those paths in which the read operation obtains the value 1012. It is easy to see that, even if there are many possible paths, each corresponding to a different value, all paths lead the read operation to obtain a value that does not exceed the value eventually written by the last write operation, that is, 2112.
10.3 Application to the Readers/Writer Problem
The underlying idea of a lock-free algorithm is to let processes read from and write into the shared data at any time without synchronizing them in any way. A reader can therefore access the shared data while they are being written and obtain an inconsistent value.
Instead of preventing this unfortunate outcome, the algorithm checks—after reading—if it might have obtained an inconsistent value. If this is the case, it retries the read operation. Intuitively, it may happen that a reader loops for a long time if write operations are “frequent enough,” so that the reader likely obtains an inconsistent value on each try.
The algorithm maintains two shared, multidigit version numbers associated with the shared data: v1 and v2. It is assumed that, initially, v1 = v2. It works as follows:
The writer increments version number v1 from left to right before starting to write into the shared data.
The writer increments version number v2 from right to left after finishing the write operation.
The reader reads version number v2 from left to right before starting to read the shared data.
The reader reads version number v1 from right to left after finishing reading of the shared data.
If the version numbers obtained before and after reading the shared data do not match, the reader retries the operation.
The corresponding C-like code, derived from the Algol code of Reference [56], is shown in Figure 10.3. In the figure,

FIGURE 10.3
C-like code of a lock-free solution to the readers/writer problem, using two multidigit version numbers, adapted from [56].
means that the read or write access to the digits of
vare performed from left to right.means that the read or write access to the digits of
vare performed from right to left.The listing shows that
v1is incremented by one; actually, the algorithm presented in Reference [56] is more general and works as long asv1is set to any value greater than its current value.Similarly, both
v1andv2are initialized to zero, although the algorithm works as long as both those variables are initialized to the same, arbitrary value.
Due to the read/write order, Theorem 10.2 states that the reader always obtains a value of v2 less than or equal to the value just written (or being written) into v2 when the read concluded. For the same reason, the value obtained by reading v1 is always greater than or equal to the value v1 had when the read began, even if that value was already being overwritten by the writer.
Since the writer increments v1 before starting to update the shared data, and increments v2 to the same value as v1 after the update is done, if the reader obtains the same value from reading v2 and v1, it also read a single, consistent version of the shared data. Otherwise, it might have obtained an inconsistent value, and it must therefore retry the operation.
Formally, the correctness of the algorithm relies on the following theorem. It states that, if the reader does not repeat the operation, then it obtained a consistent value for the shared data.
Theorem 10.3. Let D denote the shared data item. Let v2[k1,l1], D[k2,l2], and v1[k3,l3] be the values of v2, D , and v1 obtained by a reader in one single iteration of its loop.
If v2[k1,l1] = v1[k3,l3] (the reader exits from the loop and does not retry the read), then k2 = l2 (the value it obtained for D is consistent).
Proof. Theorem 10.2, applied to v2 and v1, states that
By applying Theorem 10.1 to the composite data item v = v2 D v1, we obtain
because, due to the structure of the code shown in Figure 10.3, the writer writes v from right to left, whereas readers read v from left to right. The order in which the individual digits within digit groups v2, D, and v1 are read or written is left unspecified in the code but, as stated before, none of the properties proved so far rely on this.
However, v1[0] = v2[0], and the writer starts writing v2 after writing v1. Therefore, l1 ≤ k3 from (10.18) implies that
and the equality v2[l1] = v1[k3] only holds if l1 = k3. Informally speaking, a reader gets the same numeric value for v2 and v1 if and only if it reads them after they have been incremented the same number of times by the writer. Otherwise, if it gets an older “version” of v2 than of v1, the numeric value of v2 will be lower than the value of v1.
By combining all the inequalities derived so far, namely, (10.16), (10.19), and (10.17), we obtain
Hence, v2[k1,l1] = v1[k3,l3] (the reader exits from the loop and does not retry the read) implies v2[l1] = v1[k3], but this in turn entails l1 = k3. From (10.18) we can conclude that it must also be k2 = l2, but this result implies that the reader obtained a consistent version of D, that is, D[k2,l2] with k2 = l2, and this proves the theorem.
It is interesting to point out that Theorem 10.3 is rather conservative. It states a sufficient condition for the reader to obtain a consistent version of D, but the condition is not necessary. In other words, the reader may obtain a consistent version of D although the values it got for v2 and v1 were different. More formally, it may be k2 = l2 even if v2[k1,l1] ≠ v1[k3,l3]. From a practical perspective, a reader may retry a read, even if it already obtained a consistent version of D in the previous iteration.
The comparison of the properties of the readers/writer algorithm just discussed with the general definitions given in Section 10.1 shows that the writer is wait-free. In fact, it always completes an operation after taking a finite number of steps, regardless of what the readers do or don’t, and thus it satisfies Definition 10.2.
However, the writer can interfere with concurrent read operations, forcing them to be retried. The number of tries required to successfully complete a read is unbounded. The extreme case happens when the writer halts partway along the update: any subsequent read operation will then be retried forever because the readers will always find that .
In any case, if we consider a set of readers plus one writer that does not fail, it is still true that some of them will complete an operation after the system takes a finite number of steps: the writer will definitely update the shared data and some readers may be able to read it, too. The same property also holds if we consider a set of readers without any writer, and hence, Definition 10.1 is still met. For this reason, the algorithm presented in this section is lock-free, but not wait-free.
10.4 Universal Constructions
Ad-hoc techniques, such as the algorithms described in Sections 10.2 and 10.3, have successfully been used as building blocks to construct more complex lock-free objects. However, they do not solve the problem in general terms and may be difficult to understand and prove correct. Even more importantly, the proof of correctness must be carried out again, possibly from scratch, whenever some aspects of the algorithm change.
Both aspects may hinder the adoption of those methods for real-world applications, and stimulated other authors to look for a more practical methodology. As stated by Herlihy [34],
“A practical methodology should permit a programmer to design, say, a correct lock-free priority queue without ending up with a publishable result.”
According to Herlihy’s proposal [34], an arbitrary lock-free object is designed in two steps:
The programmer implements the object as a stylized, sequential program with no explicit synchronization, following certain simple conventions.
The sequential implementation is transformed into a lock-free or wait-free implementation by surrounding its code with a general synchronization and memory management layer.
It can be proved that, if the sequential implementation is correct, the transformed implementation is correct as well.
Besides the usual atomic read and write operations on shared variables already introduced for digit access in the previous sections, Herlihy’s approach requires hardware support for
A
load_linkedoperation, which copies a shared variable into a local variable.A subsequent
store_conditionaloperation, which stores back a new value into the shared variable only if no other process has modified the same variable in the meantime.Otherwise,
store_conditionaldoes not do anything and, in particular, it does not modify the shared variable.In both cases,
store_conditionalreturns a success/failure indication.To provide room for an easier and more efficient implementation,
store_conditionalis permitted to fail, with a low probability, even if the variable has not been modified at all.
Even if this kind of requirement may seem exotic at first sight, it should be noted that most modern processors, and even some relatively low-end micro-controllers, do provide such instructions. For example, starting from version V6 of the ARM processor architecture [5], the following two instructions are available:
LDREXloads a register from memory; in addition, if the address belongs to a shared memory region, it marks the physical address as exclusive access for the executing processor.STREXperforms a conditional store to memory. The store only occurs if the executing processor has exclusive access to the memory addressed. The instruction also puts into a destination register a status value that represents its outcome. The value returned is0if the operation updated memory, or1if the operation failed to update memory.
Within this section, a concurrent system is a collection of n sequential processes. As usual, processes communicate through shared objects and are sequential, that is, any operations they invoke on the shared objects are performed in a sequence. Moreover, processes can halt at arbitrary points of their execution and exhibit arbitrary variations in speed.
Objects are typed. The type of an object defines the set of its possible values, as well as the operations that can be carried out on it. Objects are assumed to have a sequential specification that defines the object behavior when its operations are invoked sequentially by a single process.
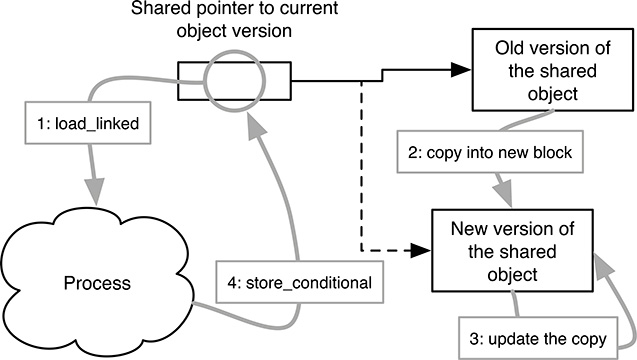
FIGURE 10.4
Basic technique to transform a sequential object implementation into a lock-free implementation of the same object.
As was done in Chapter 5, when dealing with a concurrent system, it is necessary to give a meaning to interleaved operation executions. According to the definition given in Reference [35], an object is linearizable if each operation appears to have taken place instantaneously at some point between the invocation of the operation and its conclusion.
This property implies that processes operating on a linearizable object appear to be interleaved at the granularity of complete operations. Moreover, the order of nonoverlapping operations is preserved. Linearizability is the basic correctness condition of Herlihy’s concurrent objects.
Shared objects are also assumed to be “small,” that is, they are small enough to be copied efficiently. Moreover, it is understood that a sequential object occupies a fixed-size, contiguous area of memory called a block.
Any sequential operation invoked on an object cannot have any side effect other than modifying the block occupied by the object itself. All sequential operations must also be total, that is, they must have a well-defined behavior for any legal or consistent state of the object they are invoked on. For example, a dequeue operation invoked on an empty queue is allowed to return an error indication but is not allowed to trigger a trap because it tried to execute an illegal instruction.
The basic technique to transform a sequential implementation into a lock-free implementation of a given object is shown in Figure 10.4. It is assumed that all processes share a variable that holds a pointer to the current version of the shared object and can be manipulated by means of the load_linked and store_conditional instructions. Each process acts on the object by means of the following four steps:
It reads the pointer using
load_linked.It copies the indicated version into another block.
It performs the sequential operation on the copy.
It tries to move the pointer from the old version to the new by means of
store_conditional.
If step 4 fails, it means that another process succeeded in updating the shared pointer between steps 1 and 2. In this case, the process retries the operation by restarting from step 1. Each iteration of these steps is sometimes called an attempt.
The linearizability of the concurrent implementation is straightforward to prove: from the point of view of the other processes, a certain operation appears to happen instantaneously, exactly when the corresponding store_conditional succeeds. Moreover, the order in which operations appear to happen is the same as the (total) order of their final, successful execution of store_conditional.
If store_conditional cannot fail “spontaneously,” the concurrent implementation is lock-free because, even if all the n processes in the system try to perform an operation on the shared object, at least one out of every n attempts to execute store_conditional must succeed. Hence, the system works according to Definition 10.1.
The last thing to be discussed is how the memory blocks used to hold distinct object versions should be managed keeping in mind that, in practice, only a finite number of such blocks are available, and they must therefore necessarily be reused over and over.
At first sight, it seems that n + 1 blocks of memory should suffice, provided they are used according to the following simple rules:
At each instant, each of the n processes owns a single block of unused memory.
The n + 1-th block holds the current version of the object and is not owned by any process.
In step 2, the process copies the object’s current version into its own block.
When the
store_conditionalis performed successfully in step 4, the process becomes the owner of the block that held the object’s old version. It also relinquishes the block it owned previously because it now contains the current version of the object.
However, this approach is not correct because it may lead to a race condition in object access. Let us assume, as shown in Figure 10.5, that there are two processes in the system, P and Q, and three blocks of memory, #1 to #3. The owner of each block is indicated by the block’s background. In this scenario, the following unfortunate interleaving may take place:
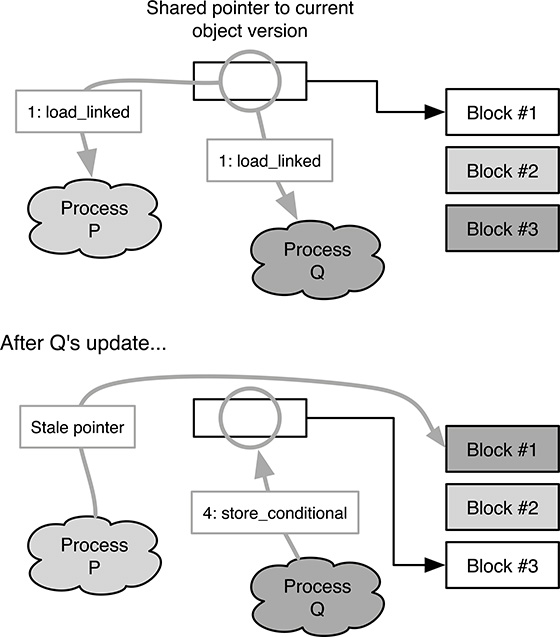
FIGURE 10.5
A careless memory management approach may lead to a race condition in object access.
At the beginning, memory block #1 holds the current object version, while P and Q own blocks #2 and #3, respectively, as shown in the upper part of Figure 10.5.
Both P and Q retrieve a pointer to the current object version, held in block #1.
Q’s update succeeds. The new version of the object is now stored in block #3, and Q has become the owner of block #1.
However, P still holds a “stale” pointer to block #1, which contains what is now an obsolete version of the object, as shown in the bottom part of the figure.
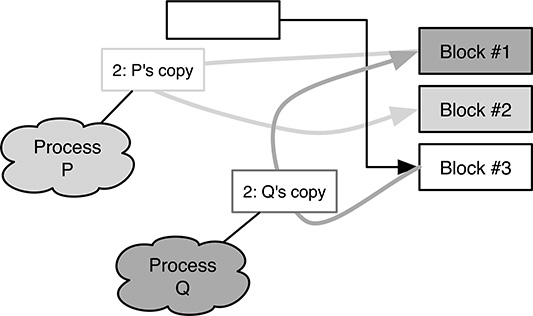
FIGURE 10.6
Making a copy of an object while it is being overwritten by another process is usually not a good idea.
If Q begins a new operation at this point, it will retrieve a pointer to the new object version in block #3 and will start copying its contents into its own block, that is, block #1. Since P is still engaged in its operation, the two copies performed by P and Q may overlap.
That is, as shown in Figure 10.6, P may read from block #1 while Q is overwriting it with the contents of block #3. As a result, with this memory management scheme, P’s copy of the shared object in block #2 may not represent a consistent state of the object itself.
It should be noted that this race condition is not harmful to the consistency of the shared object itself. In fact, when P eventually performs its store_conditional, this operation will certainly fail because Q’s store_conditional preceded it. As a consequence, P will carry out a new update attempt.
However, it poses significant issues from the software engineering point of view. Although it is (relatively) easy to ensure that any operation invoked on a consistent object will not do anything nasty (execution of illegal instructions, division by zero, etc.), this property may be extremely difficult to establish when the operation is invoked on an arbitrary bit pattern.
The issue can be addressed by inserting a consistency check between steps 2 and 3 of the algorithm, that is, between the copy and the execution of the sequential operation. If the consistency check fails, then the source object was modified during the copy. In this case, the process might have an inconsistent copy of the shared object and must retry the operation from step 1 without acting on the copy in any way.
On some architectures, the consistency check is assisted by hardware and is built upon a so-called validate instruction. Like store_conditional, this instruction checks whether a variable previously read with load_linked has been modified or not, but does not store any new value into it. If the underlying architecture does not provide this kind of support, like the ARM V6 processor architecture [5], a software-based consistency check can be used as a replacement.

FIGURE 10.7
Pseudocode of the universal construction of a lock-free object proposed in Reference [34].
In this case, two counters, C0 and C1, complement each object version. Both counters are unbounded, that is, it is assumed that they never over-flow, and start from the same value. The counters are used according to the following rules:
Before starting to modify an object, a process increments C0. After finishing, it also increments C1.
On the other hand, C1 and C0 are read before starting and after finishing to copy an object, respectively.
The consistency check consists of comparing these values: if they match, the copied object is definitely consistent; otherwise, it might be inconsistent.
An attentive reader would certainly have noticed the strong resemblance of this technique with the readers/writer algorithm discussed in Section 10.3. As in that case, if the counters cannot be read and incremented in an atomic way, incrementing the counters in one order and reading them in the opposite order is crucial to the correctness of the algorithm.
This is frequently important in practice because real-world counters cannot be unbounded in a strict sense since they have a finite size. On the other hand, if we let the counters be bounded, the consistency check may succeed incorrectly when a counter cycles all the way around during a single update attempt. The probability of this error can be made arbitrarily small by enlarging the counters, but, in this case, their size will probably exceed the maximum data size on which the architecture can perform atomic operations.
We are now ready to put all pieces together and discuss the full algorithm to build a lock-free object from a sequential one in a universal way. It is shown in Figure 10.7 as pseudocode, and its formal correctness proof was given in Reference [34]; however, we will only discuss it informally here. In the listing, Q is a shared variable that points to the current version of the shared object, and N is a local variable that points to the object version owned by the executing process.
Shared objects are assumed to be structures containing three fields: the obj field holds the object contents, while C0 and C1 are the two counters used for consistency check. The obj field does not comprise the counters; hence, when the obj field is copied from one structure to another, the counters of the destination structure are not overwritten and retain their previous value.
The algorithm starts by getting a local pointer, called
old, to the current object version, usingload_linked(step 1 of Figure 10.7).Then, the object version owned by the executing process, pointed by
N, is marked as invalid. This is done by incrementing its C0 counter using C1 as a reference. This step is very important because, as discussed before, other processes may still hold stale pointers to it (step 2).In steps 3 and 5, the counters associated to the object version pointed by
oldare copied into local variables before and after copying its contents into the object version pointed byN(step 4).After the copy, the values obtained for the two counters are compared: if they do not match, another process has worked on the object in the meantime and the whole operation must be retried (step 6).
If the consistency check was successful, then
Npoints to a consistent copy of the shared object, and the executing process can perform the intended operation on it (step 7).After the copy, the object version pointed by
Nis marked as consistent by incrementing its C1 counter (step 8). The increment brings C1 to the same value as C0, which was incremented in step 2.It is now time to publish the updated object by performing a
store_conditionalof the local object pointerNinto the shared object pointerQ(step 9). The conditional store will fail ifQwas modified by some other process since it was loaded by the executing process in step 1. In this case, the whole operation must be retried.If the conditional store was successful, the executing process can acquire ownership of the old object version (step 10).
It should be noted that the basic scheme just described is quite inefficient in some cases. For example, it is not suited for “large” objects because it relies on copying the whole object before working on it. However, other universal constructions have been proposed just for that case, for instance Reference [2]. It can also be made wait-free by means of a general technique known as operation combining and discussed in Reference [34].
10.5 Summary
In this chapter, it has been shown that it is not strictly necessary for processes to wait for each other if they must share information in an orderly and meaningful way. Rather, the lock and wait-free communication approach allows processes to perform concurrent accesses to a shared object without blocking and without introducing any kind of synchronization constraint among them.
Since, due to lack of space, it would have been impossible to fully discuss the topic, only a couple of algorithms have been considered in this chapter. They represent an example of two distinct ways of approaching the problem: the first one is a simple, ad-hoc algorithm that addresses a very specific concurrent programming problem, whereas the second one is more general and serves as a foundation to build many different classes of lock-free objects.
As a final remark, it is worth noting that, even if lock and wait-free algorithms are already in use for real-world applications, they are still an active research topic, above all for what concerns their actual implementation. The development and widespread availability of open-source libraries containing a collection of lock-free data structures such as, for example, the Concurrent Data Structures library (libcds) [52] is encouraging. More and more programmers will be exposed to them in the near future, and they will likely bring what is today considered an advanced topic in concurrent programming into the mainstream.
