Chapter 2
Mutual Exclusion Problem
2.1 Introduction
When processes share data, it is important to synchronize their access to the data so that updates are not lost as a result of concurrent accesses and the data are not corrupted. This can be seen from the following example. Assume that the initial value of a shared variable x is 0 and that there are two processes, P0 and P1 such that each one of them increments x by the following statement in some high-level programming language:
x = x + 1
It is natural for the programmer to assume that the final value of x is 2 after both the processes have executed. However, this may not happen if the programmer does not ensure that x = x + 1 is executed atomically. The statement x = x + 1 may compile into the machine-level code of the form

Now the execution of P0 and P1 may get interleaved as follows:

Thus both processes load the value 0 into their registers and finally store 1 into x resulting in the “lost update” problem.
To avoid this problem, the statement x = x + 1 should be executed atomically. A section of the code that needs to be executed atomically is also called a critical region or a critical section. The problem of ensuring that a critical section is executed atomically is called the mutual exclusion problem. This is one of the most fundamental problems in concurrent computing and we will study it in detail.
The mutual exclusion problem can be abstracted as follows. We are required to implement the interface shown in Figure 2.1. A process that wants to enter the critical section (CS) makes a call to requestCS with its own identifier as the argument. The process or the thread that makes this call returns from this method only when it has the exclusive access to the critical section. When the process has finished accessing the critical section, it makes a call to the method releaseCS.

Figure 2.1: Interface for accessing the critical section
The entry protocol given by the method requestCS and the exit protocol given by the method releaseCS should be such that the mutual exclusion is not violated.
To test the Lock, we use the program shown in Figure 2.2. This program tests the Bakery algorithm that will be presented later. The user of the program may test a different algorithm for a lock implementation by invoking the constructor of that lock implementation. The program launches N threads as specified by arg[0]. Each thread is an object of the class MyThread. Let us now look at the class MyThread. This class has two methods, nonCriticalSection and CriticalSection, and it overrides the run method of the Thread class as follows. Each thread repeatedly enters the critical section. After exiting from the critical section it spends an undetermined amount of time in the noncritical section of the code. In our example, we simply use a random number to sleep in the critical and the noncritical sections.

Figure 2.2: A program to test mutual exclusion
Let us now look at some possible protocols, one may attempt, to solve the mutual exclusion problem. For simplicity we first assume that there are only two processes, P0 and P1.
2.2 Peterson’s Algorithm
Our first attempt would be to use a shared boolean variable openDoor initialized to true. The entry protocol would be to wait for openDoor to be true. If it is true, then a process can enter the critical section after setting it to false. On exit, the process resets it to true. This algorithm is shown in Figure 2.3.
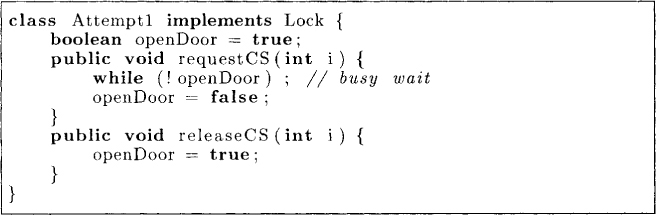
Figure 2.3: An attempt that violates mutual exclusion
This attempt does not work because the testing of openDoor and setting it to false is not done atomically. Conceivably, one process might check for the openDoor and go past the while statement in Figure 2.3. However, before that process could set openDoor to false, the other process starts executing. The other process now checks for the value of openDoor and also gets out of busy wait. Both the processes now can set openDoor to false and enter the critical section. Thus, mutual exclusion is violated.
In the attempt described above, the shared variable did not record who set the openDoor to false. One may try to fix this problem by keeping two shared variables, wantCS[0] and wantCS[1], as shown in Figure 2.4. Every process Pi first sets its own wantCS bit to true at line 4 and then waits until the wantCS for the other process is false at line 5. We have used 1 – i to get the process identifier of the other process when there are only two processes - P0 and P1. To release the critical section, Pi simply resets its wantCS bit to false. Unfortunately, this attempt also does not work. Both processes could set their wantCS to true and then indefinitely loop, waiting for the other process to set its wantCS false.

Figure 2.4: An attempt that can deadlock
Yet another attempt to fix the problem is shown in Figure 2.5. This attempt is based on evaluating the value of a variable turn. A process waits for its turn to enter the critical section. On exiting the critical section, it sets turn to 1-i.

Figure 2.5: An attempt with strict alternation
This protocol does guarantee mutual exclusion. It also guarantees that if both processes are trying to enter the critical section, then one of them will succeed. However, it suffers from another problem. In this protocol, both processes have to alternate with each other for getting the critical section. Thus, after process P0 exits from the critical section it cannot enter the critical section again until process P1 has entered the critical section. If process P1 is not interested in the critical section, then process P0 is simply stuck waiting for process P1. This is not desirable.
By combining the previous two approaches, however, we get Peterson’s algorithm for the mutual exclusion problem in a two-process system. In this protocol, shown in Figure 2.6, we maintain two flags, wantCS[0] and wantCS[1], as in Attempt2, and the turn variable as in Attempt3. To request the critical section, process Pi sets its wantCS flag to true at line 6 and then sets the turn to the other process Pj at line 7. After that, it waits at line 8 so long as the following condition is true:
(wantCS[j] && (turn == j))
Thus a process enters the critical section only if either it is its turn to do so or if the other process is not interested in the critical section.
To release the critical section, Pi simply resets the flag wantCS[i] at line 11. This allows Pj to enter the critical section by making the condition for its while loop false.

Figure 2.6: Peterson’s algorithm for mutual exclusion
We show that Peterson’s algorithm satisfies the following desirable properties:
1. Mutual exclusion: Two processes cannot be in the critical section at the same time.
2. Progress: If one or more processes are trying to enter the critical section and there is no process inside the critical section, then at least one of the processes succeeds in entering the critical section.
3. Starvation-freedom: If a process is trying to enter the critical section, then it eventually succeeds in doing so.
We first show that mutual exclusion is satisfied by Peterson’s algorithm. Assume without loss of generality that P0 was the first one to enter the critical section. To enter the critical section, P0 must have either read wantCS[1] as false, or turn as 0. We now perform a case analysis:
Case 1: P0 read wantCS[1] as false. If wantCS[1] is false, then for P1 to enter the critical section, it would have to set wantCS[1] to true. From this case, we get the following order of events: P0 reads wantCS[1] as false before P1 sets the value of wantCS[1] as true. This order of events implies that P1 would set turn = 0 before checking the entry condition and after the event of P0 reading wantCS[1]. On the other hand, P0 set turn = 1 before reading wantCS[1]. Therefore, we have the following order of events in time:
• P0 sets turn to 1.
• P0 reads wantCS[1] as false.
• P1 sets wantCS[1] as true.
• P1 sets turn to 0.
• P1 reads turn.
Clearly, turn can be only 0 when P1 reads it. Now let us look at the set of values of wantCS[0] that P1 can possibly read. From the program, we know that P0 sets wantCS[0] as true before reading wantCS[1]. Similarly, P1 sets wantCS[1] before reading wantCS[0]. We know that P0 read wantCS[1] as false. Therefore, P1 sets wantCS[1] as true after P0 reads wantCS[1]. This implies that we have the following order of events:
• P0 sets wantCS[0] as true.
• P0 reads wantCS[1] as false.
• P1 sets wantCS[1] as true.
• P1 reads wantCS[0].
Therefore, P1 can only read wantCS[0] as true. Because P1 reads turn as 0 and wantCS[0] as true, it cannot enter the critical section.
Case 2: P0 read turn as 0. This implies the following order of events: P1 sets turn = 0 between P0 setting turn = 1 and P0 reading the value of turn. Since P1 reads the value of turn only after setting turn = 0, we know that it can read turn only as 0. Also, wantCS[0] is set before P0 sets turn = 1. Therefore, P0 sets wantCS[0] before P1 sets turn = 0. This implies that P1 reads the value of wantCS[0] as true. Thus, even in this case, P1 reads turn as 0 and wantCS[0] as true. It follows that P1 cannot enter the critical section.
It is easy to see that the algorithm satisfies the progress property. If both the processes are forever checking the entry protocol in the while loop, then we get
wantCS[2] ∧ (turn = 2) ∧ wantsCS[1] ∧ (turn = 1)
which is clearly false because (turn = 2) ∧ (turn = 1) is false.
The proof of freedom from starvation is left as an exercise. The reader can also verify that Peterson’s algorithm does not require strict alternation of the critical sections—a process can repeatedly use the critical section if the other process is not interested in it.
2.3 Lamport’s Bakery Algorithm
Although Peterson’s algorithm satisfies all the properties that we initially required from the protocol, it works only for two processes. Although the algorithm can be extended to N processes by repeated invocation of the entry protocol, the resulting algorithm is more complex.
We now describe Lamport’s bakery algorithm, which overcomes this disadvantage. The algorithm is similar to that used by bakeries in serving customers. Each customer who arrives at the bakery receives a number. The server serves the customer with the smallest number. In a concurrent system, it is difficult to ensure that every process gets a unique number. So in case of a tie, we use process ids to choose the smaller process.
The algorithm shown in Figure 2.7 requires a process Pi to go through two main steps before it can enter the critical section. In the first step (lines 15–21), it is required to choose a number. To do that, it reads the numbers of all other processes and chooses its number as one bigger than the maximum number it read. We will call this step the doorway. In the second step the process Pi checks if it can enter the critical section as follows. For every other process Pj, process Pi first checks whether Pj is currently in the doorway at line 25. If Pj is in the doorway, then Pi waits for Pj to get out of the doorway. At lines 26–29, Pi waits for the number[j] to be 0 or (number[i], i) < (number[j], j). When Pi is successful in verifying this condition for all other processes, it can enter the critical section.
We first prove the assertion:
(A1) If a process Pi is in critical section and some other process Pk has already chosen its number, then (number[i], i) < (number[k], k).
If the process Pi is in critical section, then it managed to get out of the kth iteration of the for loop in the second step. This implies that either (number[k] = 0) or ((number[i], i) < (number[k], k)) at that iteration. First assume that process Pi read number[k] as 0. This means that process Pk must not have finished choosing the number yet. There are two cases. Either Pk has not entered the doorway or it has entered the doorway but not exited yet. If Pk has not entered the doorway, it will read the latest value of number[i] and is guaranteed to have number[k] > number[i]. If it had entered the doorway, then this entry must be after Pi had checked choosing[k] because Pi waits for Pk to finish choosing before checking the condition (number[k] = 0) ∨ ((number[i], i) < (number[k], k)). This again means that that Pk will read the latest value of number[i] and therefore (number[i] < number[k]). If ((number[i], i) < (number[k], k)) at the fcth iteration, this will continue to hold because number[i] does not change and number[k] can only increase.

Figure 2.7: Lamport’s bakery algorithm
We now claim the assertion:
(A2) If a process Pi is in critical section, then (number[i] > 0).
(A2) is true because it is clear from the program text that the value of any number is at least 0 and a process executes increment operation on its number at line 20 before entering the critical section.
Showing that the bakery algorithm satisfies mutual exclusion is now trivial. If two processes Pi and Pk are in critical section, then from (A2) we know that both of their numbers are nonzero. From (A1) it follows that (number[i], i) < (number[k], k) and vice versa, which is a contradiction.
The bakery algorithm also satisfies starvation freedom because any process that is waiting to enter the critical section will eventually have the smallest nonzero number. This process will then succeed in entering the critical section.
It can be shown that the bakery algorithm does not make any assumptions on atomicity of any read or write operation. Note that the bakery algorithm does not use any variable that can be written by more than one process. Process Pi writes only on variables number[i] and choose[i].
There are two main disadvantages of the bakery algorithm: (1) it requires O(N) work by each process to obtain the lock even if there is no contention, and (2) it requires each process to use timestamps that are unbounded in size.
2.4 Hardware Solutions
As we have seen, pure software solutions to mutual exclusion can be quite complex and expensive. However, mutual exclusion can be provided quite easily with the help of hardware. We discuss some techniques below.
2.4.1 Disabling Interrupts
In a single-CPU system, a process may disable all the interrupts before entering the critical section. This means that the process cannot be context-switched (because context switching occurs when the currently running thread receives a clock interrupt when its current timeslice is over). On exiting the critical section, the process enables interrupts. Although this method can work for a single-CPU machine, it has many undesirable features. First, it is infeasible for a multiple-CPU system in which even if interrupts are disabled in one CPU, another CPU may execute. Disabling interrupts of all CPUs is very expensive. Also, many system facilities such as clock registers are maintained using hardware interrupts. If interrupts are disabled, then these registers may not show correct values. Disabling interrupts can also lead to problems if the user process has a bug such as an infinite loop inside the critical section.
2.4.2 Instructions with Higher Atomicity
Most machines provide instructions with a higher level of atomicity than read or write. The testAndSet instruction provided by some machines does both read and write in one atomic instruction. This instruction reads and returns the old value of a memory location while replacing it with a new value. We can abstract the instruction as a testAndSet method on an object of the class TestAndSet as shown in Figure 2.8.

Figure 2.8: TestAndSet hardware instruction
If the testAndSet instruction is available, then one can develop a very simple protocol for mutual exclusion as shown in Figure 2.9.

Figure 2.9: Mutual exclusion using TestAndSet
This algorithm satisfies the mutual exclusion and progress property. However, it does not satisfy starvation freedom. Developing such a protocol is left as an exercise.
Sometimes machines provide the instruction swap, which can swap two memory locations in one atomic step. Its semantics is shown in Figure 2.10. The reader is invited to design a mutual exclusion protocol using swap.
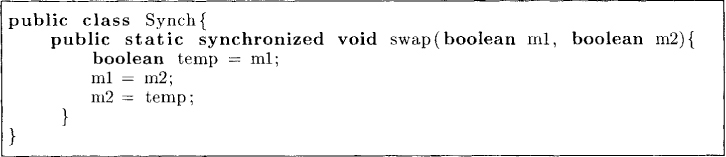
Figure 2.10: Semantics of swap operation
2.5 Problems
2.1. Show that any of the following modifications to Peterson’s algorithm makes it incorrpet:
(a) A process in Peterson’s algorithm sets the turn variable to itself instead of setting it to the other process.
(b) A process sets the turn variable before setting the wantCS variable.
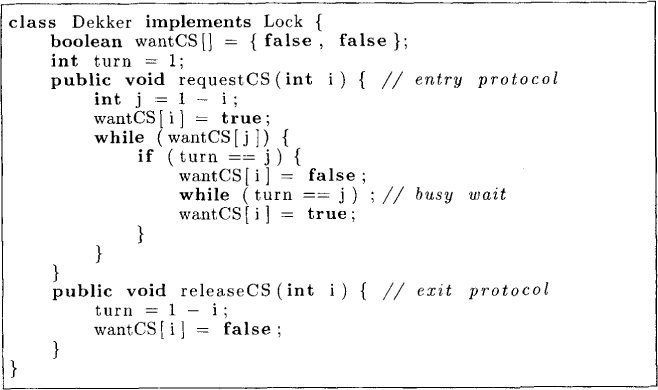
Figure 2.11: Dekker.java
2.2. Show that Peterson’s algorithm also guarantees freedom from starvation.
2.3. Show that the bakery algorithm does not work in absence of choosing variables.
2.4. Consider the software protocol shown in Figure 2.11 for mutual exclusion between two processes. Does this protocol satisfy (a) mutual exclusion, and (b) livelock freedom (both processes trying to enter the critical section and none of them succeeding)? Does it satisfy starvation freedom?
2.5. Modify the bakery algorithm to solve k-mutual exclusion problem, in which at most k processes can be in the critical section concurrently.
2.6. Give a mutual exclusion algorithm that uses atomic swap instruction.
2.7. Give a mutual exclusion algorithm that uses TestAndSet instruction and is free from starvation.
*2.8. Give a mutual exclusion algorithm on N processes that requires O(1) time in absence of contention.
2.6 Bibliographic Remarks
The mutual exclusion problem was first introduced by Dijkstra [Dij65a]. Dekker developed the algorithm for mutual exclusion for two processes. Dijkstra [Dij65b] gave the first solution to the problem for N processes. The bakery algorithm is due to Lamport [Lam74], and Peterson’s algorithm is taken from a paper by Peterson [Pet81].
