Chapter 15

Agreement

15.1 Introduction

Consensus is a fundamental problem in distributed computing. Consider a distributed database in which a transaction spans multiple sites. In this application it is important that either all sites agree to commit or all sites agree to abort the transaction. In absence of failures, this is a simple task. We can use either a centralized scheme or a quorum-based scheme. What if processes can fail? It may appear that if links are reliable, the system should be able to tolerate at least failure of a single process. In this chapter, we show the surprising result that even in the presence of one unannounced process death, the consensus problem is impossible to solve. This result (FLP) is named after Fischer, Lynch and Paterson who first discovered it.

The FLP result for consensus shows a fundamental limitation of asynchronous computing. The problem itself is very basic—processes need to agree on a single bit. Most problems we have discussed such as leader election, mutual exclusion, and computation of global functions are harder than the consensus problem because any solution to these problems can be used to solve the consensus problem. The impossibility of consensus implies that all these problems are also impossible to solve in the presence of process failures.

The FLP result is remarkable in another sense. It assumes only a mild form of failures in the environment. First, it assumes only process failures and not link failures. Any message sent takes a finite but unbounded amount of time. Furthermore, it assumes that a process fails only by crashing and thus ceasing all its activities. Thus it does not consider failures in which the process omits certain steps of the protocol or colludes with other processes to foil the protocol. Since the impossibility result holds under weak models of failure, it is also true for stronger failure models.

15.2 Consensus in Asynchronous Systems (Impossibility)

The consensus problem is as follows. We assume that there are N, (N ≥ 2) processes in the system and that the value of N is known to all processes. Each process starts with initial value of {0,1}. This is modeled as a one bit input register x. A nonfaulty process decides by entering a decision state. We require that some process eventually make a decision. Making a decision is modeled by output registers. Each process also has an output register y that indicates the value decided or committed on by the process. The value of 0 in y indicates that the process has decided on the value 0. The same holds for the value 1. The value ┴ indicates that the process has not agreed on any value. Initially, we require all processes to have ┴ in their register y. We require that once a process has decided, it does not change its value, that is, output registers are write-once. We also assume that each process has unbounded storage.

Figure 15.1: (a) Commutativity of disjoint events; (b) asynchrony of messages

Before we list formal requirements of the consensus problem, we discuss our assumptions on the environment.

• Initial independence: We allow processes to choose their input in an independent manner. Thus, all input vectors are possible.

• Commute property of disjoint events: Let G be any global state such that two events e and f are enabled in it. If e and f are on different processes, then they commute. This is shown in Figure 15.1(a). We use the notation e(G) for the global state reached after executing event e at G. Similarly, we use s(G) to denote the global state reached after executing a sequence of events s at the global state G. The global state reached after executing ef at G is identical to the one reached after executing fe at G.

• Asynchrony of events: The asynchronous message system is modeled as a buffer with two operations. The operation send(p, m) by process p places (p, m) in the buffer. The operation receive() from p by any process q deletes (p, m) and returns m or returns null. The system may return null to model the fact that the asynchronous messages may take an unbounded amount of time. The condition we impose on the message system is that if the receive() event is performed an unbounded number of times, then every message is eventually delivered. The asynchrony assumption states that any receive event may be arbitrarily delayed. In Figure 15.1(b), the event e is an enabled event after executing a sequence of events s at state G because e ∉ s. Note that this assumption does not state that se(G) = es(G). The event e commutes with s only when the process on which e is executed is completely disjoint from processes that have events in s.

Our model of a faulty process is as follows. We only consider infinite runs. A faulty process is one that takes only a finite number of steps in that run. A run is admissible if at most one process is faulty. Since the message system is reliable, all messages sent to nonfaulty processes are eventually delivered. A run is deciding if some process reaches a decision state in that run.

The requirements of the protocol can be summarized as:

• Agreement: Two nonfaulty processes cannot commit on different values.

• Nontriviality: Both values 0 and 1 should be possible outcomes. This requirement eliminates protocols that return a fixed value 0 or 1 independent of the initial input.

• Termination: A nonfaulty process decides in finite time.

We now show the FLP result—there is no protocol that satisfies agreement, nontriviality, and termination in an asynchronous system in presence of one fault. The main idea behind the proof consists of showing that there exists an admissible run that remains forever indecisive. Specifically, we show that (1) there is an initial global state in which the system is indecisive, and (2) there exists a method to keep the system indecisive.

To formalize the notion of indecision, we use the notion of valences of a global state. Let G.V be the set of decision values of global state reachable from G. Since the protocol is correct, G.V is nonempty. We say that G is bivalent if |G.V| = 2 and univalent if |G.V| = 1. In the latter case, we call G 0-valent if G.V = {0} and 1-valent if G.V = {1}. The bivalent state captures the notion of indecision.

We first show that every consensus protocol has a bivalent initial global state. Assume, if possible, that the protocol does not have any bivalent initial global state. By the nontriviality requirement, the protocol must have both 0-valent and 1-valent global states. Let us call two global states adjacent if they differ in the local state of exactly one process. Since any two initial global states can be connected by a chain of initial global states each adjacent to the next, there exist adjacent 0-valent and 1-valent global states. Assume that they differ in the state of p. We now apply to both of these global states a sequence in which p takes no steps. Since they differ only in the state of p, the system must reach the same decision value, which is a contradiction.

Our next step is to show that we can keep the system in an indecisive state. Let G be a bivalent global state of a protocol. Let event e on process p be applicable to G, and g be the set of global states reachable from G without applying e. Let ℋ = e(g). We claim that ℋ contains a bivalent global state. Assume, if possible, that ℋ contains no bivalent global states. We show a contradiction.

We first claim that ℋ contains both 0-valent and 1-valent states. Let E_i (i ∈ {0..1}) be an i-valent global state reachable from G. If E_i ∈ g, then define F_i ∈ e(E_i,). Otherwise, e was applied in reaching E_i. In this case, there exists F_i ∈ ℋ from which E_i is reachable. Thus ℋ contains both 0-valent and 1-valent states.

We call two global states neighbors if one results from the other in a single step.

We now claim that there exist neighbors G₀, G₁ such that H₀ = e(G₀) is 0-valent, and H₁ = e(G₁) is 1-valent. Let t be the smallest sequence of events applied to G without applying e such that et(G) has different valency from e(G). To see that such a sequence exists, assume that e(G) is 0-valent. From our earlier claim about ℋ, there exists a global state in ℋ which is 1-valent. Let t be a minimal sequence that leads to a 1-valent state. The case when e(G) is 1-valent is similar. The last two global states reached in this sequence give us the required neighbors. Without loss of generality let G₁ = f(G₀), where f is an event on process q. We now do a case analysis:

Case 1: p is different from q [see Figure 15.2(a)]

This implies that f is applicable to H₀, resulting in H₁. This is a contradiction because H₀ is 0-valent, and H₁ is 1-valent.

Case 2: p = q [see Figure 15.2(b)]

Consider any finite deciding run from G₀ in which p takes no steps. Let s be the corresponding sequence. Let K = s(G₀). From the commute property, s is also applicable to H_i and leads to i-valent global states E_i = s(H_i). Again, by the commute property, e(K) = E₀ and e(f(K)) = E₁. Hence K is bivalent, which is a contradiction.

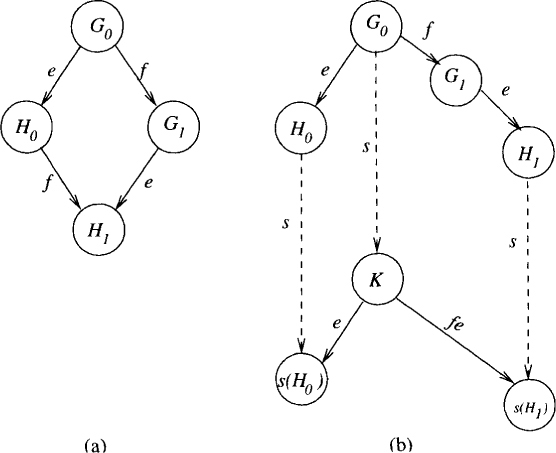
Figure 15.2: (a) Case 1: proc(e) ≠ proc(f); (b) case 2: proc(e) = proc(f)

The intuition behind the case analysis above is as follows. Any protocol that goes from a bivalent global state to a univalent state must have a critical step in which the decision is taken. This critical step cannot be based on the order of events done by different processes because execution of events at different processes commutes. This observation corresponds to case 1. This implies that the critical step must be taken by one process. But this method also does not work because other processes cannot distinguish between the situation when this process is slow and the situation when the process has crashed. This observation corresponds to case 2.

We are now ready for the main result that no consensus protocol satisfies agreement, nontriviality, and termination despite one fault. To show this result, we construct an admissible nondeciding run as follows. The run is started from any bivalent initial global state Go and consists of a sequence of stages. We ensure that every stage begins from a bivalent global state G. We maintain a queue of processes and maintain the message buffer as a FIFO queue. In each stage the process p at the head of the queue receives the earliest message m (if any). Let e be the event corresponding to p receiving the message m. From our earlier claims, we know that there is a bivalent global state H reachable from G by a sequence in which e is the last event applied. We then move the process to the back of the queue and repeat this set of steps forever. This method guarantees that every process executes infinitely often and every message sent is eventually received. Thus, the protocol stays in bivalent global states forever.

15.3 Application: Terminating Reliable Broadcast

Impossibility of consensus in the presence of a failure implies that many other interesting problems are impossible to solve in asynchronous systems as well. Consider, for example, the problem of the terminating reliable broadcast specified as follows. Assume that there are N processes in the system P₀, . . . , P_N–1 and that P₀ wishes to broadcast a single message to all processes (including itself). The terminating reliable broadcast requires that a correct process always deliver a message even if the sender is faulty and crashes during the protocol. The message in that case may be “sender faulty.” The requirements of the problem are

• Termination: Every correct process eventually delivers some message.

• Validity: If the sender is correct and broadcasts a message m, then all correct processes eventually deliver m.

• Agreement: If a correct, process delivers a message m, then all correct processes deliver m.

• Integrity: Every correct process delivers at most one message, and if it delivers m different from “sender faulty,” then the sender must have broadcast m.

We now show that the terminating reliable broadcast (TRB) is impossible to solve in an asynchronous system. We show this by providing an algorithm for consensus given an algorithm for TRB. The algorithm for consensus is simple. Process P₀ is required to broadcast its input bit using the TRB protocol. If a correct process receives a message different from “sender faulty” it decides on the bit received; otherwise, it, decides on 0. It is easy to verify that this algorithm satisfies the termination, agreement, and nontriviality requirements of the consensus problem.

15.4 Consensus in Synchronous Systems

We have seen that consensus is impossible to solve in asynchronous systems even in the presence of a single crash. We show that the main difficulty in solving consensus lies in the asynchrony assumption. Thus there exist protocols to solve consensus when the system is synchronous. A system is synchronous if there is an upper bound on the message delay and on the duration of actions performed by processes. We show that under suitable conditions not only crash failures but also malevolent faults in which faulty processes can send arbitrary messages can be tolerated by consensus algorithms.

In general, we can classify the faults in a distributed system as follows:

• Crash: In the crash model, a fault corresponds to a processor halting. When the processor halts, it does not perform any other action and stays halted forever. The processor does not perform any wrong operation such as sending a corrupted message. As we have seen earlier, crashes may not be detectable by other processors in asynchronous systems, but they are detectable in synchronous systems.

• Crash + link: In this model, either a processor can crash or a link may go down. If a link goes down, then it stays down. When we consider link failures, it is sometimes important to distinguish between two cases—one in which the network is partitioned and the second in which the underlying communication graph stays connected. When the network gets partitioned, some pairs of nodes can never communicate with each other.

• Omission: In this model, a processor fails either by sending only a proper subset of messages that it is required to send by the algorithm or by receiving only a proper subset of messages that have been sent to it. The fault of the first kind is called a send omission, and that of the second kind is called a receive omission.

• Byzantine failure: In this model, a processor fails by exhibiting arbitrary behavior. This is an extreme form of a failure. A system that can tolerate a Byzantine fault can tolerate any other fault.

In this chapter, we will consider only the crash and Byzantine failures. We assume that links are reliable for crash failures. A processor that is not faulty is called a correct processor.

15.4.1 Consensus under Crash Failures

In this section, we will be concerned mainly with algorithms for synchronous systems. It is generally advantageous to prove impossibility results with as weak a specification of the problem as possible because the same proof will hold for a stronger specification. However, when designing algorithms it is better for the algorithm to satisfy a strong specification because the same algorithm will work for all weaker specifications.

We first generalize the set of values on which consensus is required. Instead of a single bit, the set of values can be any totally ordered set. We will assume that each process P_i has as its input a value v_i from this set. The goal of the protocol is to set the value y at each process such that the following constraints are met. The value y can be set at most once and is called the value decided by the process. Thus the requirements of the protocol are:

• Agreement: Two nonfaulty processes cannot decide on different values.

• Validity: If all processes propose the same value, then the decided value should be that proposed value. It is easy to verify that this condition implies the nontriviality condition discussed in Section 15.2.

• Termination: A nonfaulty process decides in finite time.

An algorithm for achieving consensus in the presence of crash failures is quite simple. In the algorithm we use the parameter f to denote the maximum number of processors that can fail. The algorithm shown in Figure 15.3 works based on rounds. Each process maintains V, which contains the set of values that it knows have been proposed by processors in the system. Initially, a process P_i knows only the value it proposed. The algorithm takes f + 1 rounds for completion; thus the algorithm assumes that the value of f is known. In each round, a process sends to all other processes, values from V that it, has not sent before. So, initially the process sends its own value and in later rounds it sends only those values that it learns for the first time in the previous round. In each round, the processor P_i also receives the values sent by P_j. In this step, we have used the synchrony assumption. P_i waits for a message from P_j for some fixed predetermined time after which it assumes that P_j has crashed. After f + 1 rounds, each process decides on the minimum value in its set V.

The algorithm presented above satisfies termination because each correct process terminates in exactly f + 1 rounds. It satisfies validity because the decided value is chosen from the set V, which contains only the proposed values. We show the agreement property: All correct processors decide on the same value.

Figure 15.3: Algorithm at P_i for consensus under crash failures

Let V_i denote the set of values at P_i after the round f + 1. We show that if any value x is in the set V_i for some correct processor P_i, then it is also in the set V_j for any other correct processor P_j.

First assume that the value x was added to V_i in a round k < f + 1. Since P_i and P_j are correct processes, P_j will receive that value in round k + 1 and will therefore be present in V_j after round f + 1.

Now assume that the value x was added to V_i in the last round (round number f + 1). This implies that there exists a chain of f + 1 distinct processors that transferred the value from one of the processors that had x as its input value to P_i. If all the processors in the chain are faulty, then we contradict the assumption that there are at most f faulty processors. If any processor in the chain is nonfaulty, then it would have succeeded in sending x to all the processors in that round. Hence x was also added to V_j by at most f + 1 rounds.

The preceding algorithm requires O((f + 1)N²) messages because each round requires every process to send a message to all other processes. If each value requires b bits, then the total number of communication bits is O(bN³) bits because each processor may relay up to N values to all other processors.

The implementation of the above algorithm in Java is given in Figure 15.4. In this implementation we require every process to simply maintain the smallest value that it knows in the variable myValue. The variable changed records whether the minimum value it knows changed in the last round. The process broadcasts its value only if changed is true.

A simple program that calls the Consensus object is shown in Figure 15.5.

Figure 15.4: Consensus in a synchronous environment

Figure 15.5: Consensus tester

15.4.2 Consensus under Byzantine Faults

Byzantine faults allow for malicious behavior by the processes. The consensus problem in this model can be understood in the context of the Byzantine General Agreement problem, which is defined as follows. There were N Byzantine generals who were called out to repel the attack by a Turkish Sultan. These generals camped near the Turkish army. Each of the N Byzantine generals had a preference for whether to attack the Turkish army or to retreat. The Byzantine armies were strong enough that the loyal generals of the armies knew that if their actions were coordinated (either attack or retreat), then they would be able to resist the Sultan’s army. The problem was that some of the generals were treacherous and would try to foil any protocol that loyal generals might devise for the coordination of the attack. They might, for example, send conflicting messages to different generals, and might even collude to mislead loyal generals. The Byzantine General Agreement (BGA) problem requires us to design a protocol by which the loyal generals can coordinate their actions. It is assumed that generals can communicate with each other using reliable messengers.

The BGA problem can easily be seen as the consensus problem in a distributed system under Byzantine faults. We call a protocol f-resilient if it can tolerate f Byzantine faulty processors. It has been shown that there is no f-resilient protocol for BGA if N ≤ 3f.

In this section we give an algorithm that takes f + 1 rounds, each round of two phases, to solve the BGA problem. This algorithm uses constant-size messages but requires that N > 4f. Each processor has a preference for each round, which is initially its input value.

The algorithm is shown in Figure 15.6. The algorithm is based on the idea of a rotating coordinator (or king). Processor P_i is assumed to be the coordinator or the king for round k. In the first phase of a round, each processor exchanges its value with all other processors. Based on its V vector, it determines its estimate in the variable myvalue. In the second phase, the processor receives the value from the coordinator. If it receives no value (because the coordinator has failed), then it assumes v_┴ (a default value) for the king value. Now, it decides whether to use its own value or the kingvalue. This decision is based on the multiplicity of myvalue in the vector V. If V has more than N/2 + f copies of myvalue, then myvalue is chosen for V[i]; otherwise, kingvalue is used.

We first show that agreement persists, that is, if all correct processors prefer a value v at the beginning of a round, then they continue to do so at the end of a round. This property holds because

N > 4f

≡ N – N/2 > 2f

≡ N – f > N/2 + f

Since the number of correct processors is at least N - f, each correct processor will receive more than N/2 + f copies of v and hence choose that at the end of second phase.

We now show that the algorithm in Figure 15.6 solves the agreement problem. The validity property follows from the persistence of agreement. If all processors start with the same value v, then v is the value decided. Termination is obvious because the algorithm takes exactly f + 1 rounds. We now show the agreement property. Since there are f + 1 rounds and at most f faulty processors, at least one of the rounds has a correct king. Each correct processor decides on either the value sent by the king in that round or its own value. It chooses its own value w only if its multiplicity in V is at least N/2 + f + 1. Therefore, the king of that round must have at least N/2 + 1 multiplicity of w in its vector. Thus the value chosen by the king is also w. Hence, each processor decides on the same value at the end of a round in which the king is nonfaulty. From persistence of agreement, the agreement property at the end of the algorithm follows.

15.5 Knowledge and Common Knowledge

Many problems in a distributed system arise from the lack of global knowledge. By sending and receiving messages, processes increase the knowledge they have about the system. However, there is a limit to the level of knowledge that can be attained. We use the notion of knowledge to prove some fundamental results about distributed systems. In particular, we show that agreement is impossible to achieve in an asynchronous system in the absence of reliable communication.

Figure 15.6: An algorithm for Byzantine General Agreement

The notion of knowledge is also useful in proving lower bounds on the message complexity of distributed algorithms. In particular, knowledge about remote processes can be gained in an asynchronous distributed system only by message transfers. For example, consider the mutual exclusion problem. It is clear that if process P_i enters the critical section and later process P_j enters the critical section, then there must be some knowledge gained by process P_j before it can begin eating. This gain of knowledge can happen only through a message transfer. Observe that our assumption of asynchrony is crucial in requiring the message transfer. In a synchronous system with a global clock, the knowledge can indeed be gained simply by passage of time. Thus for a mutual exclusion algorithm, one may have time-division multiplexing in which processes enter the critical section on their preassigned slots. Thus mutual exclusion can be achieved without any message transfers.

Let G be a group of processes in a system. We use K_i(b) to denote that the process i in the group G knows the predicate b. We will assume that a process can know only true predicates:

K_i(b) ⇒ b

The converse may not be true. A predicate b may be true, but it may not be known to process i. For example, let b be that there is a deadlock in the system. It is quite possible that b is true but, process i does not know about it.

Now, it is easy to define the meaning of “someone in the group knows b,” denoted by S(b), as follows:

Similarly, we define “everyone in the group knows b,” denoted by E(b), as

It is important to realize that S(b) and E(b) are also predicates—in any system state they evaluate to true or false. Thus it makes perfect sense to use E(b) or S(b) for a predicate. In particular, E(E(b)) means that everyone in the group knows that everyone in the group knows b.

This observation allows us to define E^k(b), for k ≥ 0, inductively as follows:

E⁰(b) = b
E^{k +1}(b) = E(E^k(b))

It is important to realize that although

∀k: E^k+1(b) ⇒ E^k(b)

the converse does not hold in general. To appreciate this fact, consider the following scenario. Assume that there are n ≥ 1 children who have gone out to play. These children were told before they went for play, that they should not get dirty. However, children being children, k ≥ 1 of the children have dirty foreheads. Now assume that the children stand in a circle such that every child can see everyone else but cannot see his or her own forehead. Now consider the following predicate b:

In this case E^k–1(b) is true but E^k(b) is not. For concreteness, let n be 10 and k be 2. It is clear that since k is 2, b is true. Furthermore, since every child can see at least one other child with a dirty forehead, E(b) is also true. Is E²(b) true? Consider a child, say, child i with a dirty forehead. That child can see exactly one other child, say, child j, with a dirty forehead. So from child i’s perspective, there may be just one child, namely, child j, who has a dirty forehead. However, in that case child j would not know that b is true. Thus K_i(E(b)) does not hold; therefore, E²(b) is also false.

The next higher level of knowledge, called common knowledge and denoted by C(b), is defined as

It is clear that for any k,

C(b) ⇒ E^k(b).

In the example of the children with a dirty forehead, assume that one of the parents walks to the children and announces “At least one of you has a dirty forehead.” Every child hears the announcement. Not only that; they also know that everybody else heard the announcement. Furthermore, every child knows that every other child also knows this. We could go on like that. In short, by announcing b, the level of knowledge has become C(b).

Now, assume that the parent repeatedly asks the question: “Can anyone prove that his or her own forehead is dirty?” Assuming that all children can make all logical conclusions and they reply simultaneously, it can be easily shown using induction that all children reply “No” to the first k – 1 questions and all the children with a dirty forehead reply “Yes” to the kth question (see Problem 15.11).

To understand the role of common knowledge, consider the scenario when k ≥ 2. At first, it may seem that the statement made by the parent “At least one of you has a dirty forehead.” does not add any knowledge because every child can see at least one other child with a dirty forehead and thus already knew b. But this is not true. To appreciate this the reader should also consider a variant in which the parent repeatedly asks: “Can anyone prove that his or her own forehead is dirty?” witshout first announcing b. In this case, the children will never answer “Yes.” By announcing b, the parent gives common knowledge of b and therefore E^k(b). E^k(b) is required for the children to answer “Yes” in the kth round.

15.6 Application: Two-General Problem

We now prove a fundamental result about common knowledge—it cannot be gained in a distributed system with unreliable messages. We explain the significance of the result in the context of the coordinating general problem under unreliable communication. Assume that there are two generals who need to coordinate an attack on the enemy army. The armies of the generals are camped on the hills surrounding a valley, which has the enemy army. Both the generals would like to attack the enemy army simultaneously because each general’s army is outnumbered by the enemy army. They had no agreed-on plan beforehand, and on some night they would like to coordinate with each other so that both attack the enemy the next day. The generals are assumed to behave correctly, but the communication between them is unreliable. Any messenger sent from one general to the other may be caught by the enemy. The question is whether there exists a protocol that allows the generals to agree on a single bit denoting attack or retreat.

It is clear that in the presence of unreliable messages no protocol can guarantee agreement for all runs. None of the messages sent by any general may reach the other side. The real question is whether there is some protocol that can guarantee agreement for some run (for example, when some messages reach their destination). Unfortunately, even in a simple distributed system with just two processors, P and Q, that communicate with unreliable messages, there is no protocol that allows common knowledge to be gained in any of its run.

If not, let r be a run with the smallest number of messages that achieves common knowledge. Let m be the last message in the run. Assume without loss of generality that the last message was sent from the processor P to processor Q. Since messages are unreliable, processor P does not know whether Q received the message. Thus, if P can assert C(b) after m messages, then it can also do so after m – 1 messages. But C(b) at P also implies C(b) at Q. Thus C(b) is true after m – 1 messages, violating minimality of the run T.

In contrast, the lower levels of knowledge are attainable. Indeed, to go from S(b) to E(b), it is sufficient for the processor with the knowledge of b to send messages to all other processors indicating the truthness of b. In the run in which all messages reach their destination, E(b) will hold. The reader should also verify that E²(b) will not hold for any run after the protocol. The reader is asked to design a protocol that guarantees E²(b) from S(b) in one of its runs in Problem 15.12.

15.7 Problems

    15.1. Why does the following algorithm not work for consensus under FLP assumptions? Give a scenario under which the algorithm fails. It is common knowledge that there are six processes in the system numbered P₀ to P₅. The algorithm is as follows: Every process sends its input bit to all processes (including itself) and waits for five messages. Every process decides on the majority of the five bits received.

    15.2. Show that all the following problems are impossible to solve in an asynchronous system in the presence of a single failure.

(a) Leader Election: Show that the special case when the leader can be only from the set {P₀, P₁} is equivalent to consensus.

(b) Computation of a global function: Show that a deterministic nontrivial global function such as min, max, and addition can be used to solve consensus.

  15.3. Atomic broadcast requires the following properties.

• Validity: If the sender is correct and broadcasts a message m, then all correct processes eventually deliver m.

• Agreement: If a correct process delivers a message m, then all correct processes deliver m.

• Integrity: For any message m, q receives m from p at most once and only if p sent m to q.

• Order: All correct processes receive all broadcast messages in the same order.

Show that atomic broadcast is impossible to solve in asynchronous systems.

  *15.4. (due to Fischer, Lynch and Paterson[FLP85]) Show that if it is known that processes will not die during the protocol, then consensus can be reached (despite some initially dead processes).

  *15.5. Give a randomized algorithm that achieves consensus in an asynchronous distributed system in the presence of f crash failures under the assumption that N ≥ 2f + 1.

    15.6. Show by an example that if the consensus algorithm decided the final value after f rounds instead of f + 1 rounds, then it might violate the agreement property.

    15.7. Give an example of an execution of a system with six processes, two of which are faulty in which the Byzantine general agreement algorithm does not work correctly.

    15.8. Give an algorithm that solves BGA problem whenever N ≥ 3f + 1.

  *15.9. [due to Dolev and Strong[DS83]] In the Byzantine failure model a faulty process could forward incorrect information about messages received from other processes. A less malevolent model is called Byzantine failure with mutual authentication. In this model, we assume that a message can be signed digitally for authentication. There exist many cryptographic algorithms for digital signatures. Give an algorithm for Byzantine General Agreement assuming authentication that is f-resilient for f < N, requires only f + 1 rounds, and uses a polynomial number of messages.

*15.10. Show that the number of rounds required to solve consensus under the crash model is at least f + 1 in the worst case when f ≤ N – 2.

  15.11. Show using induction on k that when the parent repeatedly asks the question all children reply “NO” to the first k - 1 questions and all the children with a dirty forehead reply “Yes” to the kth question.

  15.12. Design a protocol that guarantees E²(b) from S(b) in one of its runs.

  15.13. Consider a game in which two people are asked to guess each other’s number. They are told that they have consecutive natural numbers. For example, the person with number 50 can deduce that the other person has either 51 or 49. Now they are repeatedly asked in turn “Can you tell the other person’s number?” Will any of them ever be able to answer in the affirmative? If yes, how? If no, why not?

15.8 Bibliographic Remarks

The theory of the consensus problem and its generalizations is quite well developed. We have covered only the very basic ideas from the literature. The reader will find many results in the book by Lynch [Lyn96]. The impossibility of achieving consensus in asynchronous system is due to Fischer, Lynch, and Paterson [FLP85]. The consensus problem with Byzantine faults was first introduced and solved by Lamport, Shostak and Pease [LSP82, PSL80]. The lower bound on the number of bounds needed for solving the problem under Byzantine faults was given by Fischer and Lynch [FL82] and under crash failures by Dolev and Strong [DS83].

The discussion of knowledge and common knowledge is taken from a paper by Halpern and Moses[HM84]. The “two-generals problem” was first described by [Gra78].