Chapter 18

Self-Stabilization

18.1 Introduction

In this chapter we discuss a class of algorithms, called self-stabilizing algorithms, that can tolerate many kinds of “data” faults. A “datal” fault corresponds to change in value of one or more variable of a program because of some unforeseen error. For example, a spanning tree is usually implemented using parent variables. Every node in the computer network maintains the parent pointer that points to the parent in the spanning tree. What if one or more of the parent pointers get corrupted? Now, the parent pointers may not form a valid spanning tree. Such errors will be called “data” faults. We will assume that the code of the program does not get corrupted. Because the code of the program does not change with time, it can be periodically checked for correctness using a copy stored in the secondary storage.

We assume that the system states can be divided into legal and illegal states. The definition of the legal state is dependent on the application. Usually, system and algorithm designers are very careful about transitions from the legal states, but illegal states of the system are ignored. When a fault occurs, the system moves to an illegal state and if the system is not designed properly, it may continue to execute in illegal states. A system is called self-stabilizing if regardless of the initial state, the system is guaranteed to reach a legal state after a finite number of moves.

We will illustrate the concept of self-stabilizing algorithms for two problems: mutual exclusion and spanning tree construction.

18.2 Mutual Exclusion with K-State Machines

We will model the mutual exclusion problem as follows. A machine can enter the critical section only if it has a privilege. Therefore, in the case of mutual exclusion, legal states are those global states in which exactly one machine has a privilege. The goal of the self-stabilizing mutual exclusion algorithm is to determine who has the privilege and how the privileges move in the network.

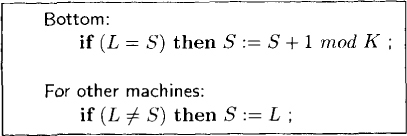
Figure 18.1: K-state self-stabilizing algorithm

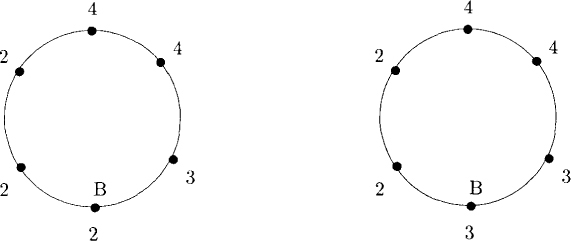
Figure 18.2: A move by the bottom machine in the K-state algorithm

We assume that there are N machines numbered 0... N — 1. The state of any machine is determined by its label from the set {0... K - 1}. We use L, S, and R to denote the labels of the left neighbor, itself, and the right neighbor for any machine. Machine 0, also called the bottom machine, is treated differently from all other machines. The program is given in Figure 18.1, and a sample execution of the algorithm is shown in Figure 18.2. The bottom machine has a privilege if its label has the same value as its left neighbor, (i.e., L = S). In Figure 18.2, the bottom machine and its left neighbor have labels 2, and therefore the bottom machine has a privilege. Once a machine possessing a privilege executes its critical section, it should execute the transition given by the program. In Figure 18.2, on exiting from the critical section, the bottom machine executes the statement S := S + 1 mod K and acquires the label 3.

A normal machine has a privilege only when L ≠ S. On exiting the critical section, it executes S := L and thus loses its privilege. In Figure 18.3, P₅ moves and makes it label as 4.

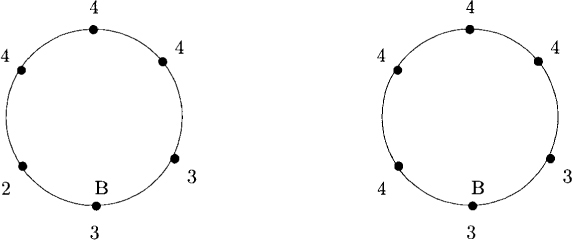
Figure 18.3: A move by a normal machine in the K-state algorithm

In this algorithm, the system is in a legal state if exactly one machine has the privilege. It is easy to verify that (x₀, x₁, . . . , x_N–1) is legal if and only if either all x_i values are equal or there exists m < N - 1 such that all x_i values with i ≤ m are equal to some value and all other x_i values are equal to some other value. In the first case, the bottom machine has the privilege. In the second case the machine P_m+1 has the privilege. It is easy to verify that if the system is in a legal state, then it will stay legal.

It is also easy to verify that in any configuration, at least one move is possible. Now we consider any unbounded sequence of moves. We claim that a sequence of moves in which the bottom machine does not move is at most O(N²). This is because machine 1 can move at most once if the bottom machine does not move. This implies that the machine 2 can move at most twice and so on. Thus, the total number of moves is bounded by O(N²).

We now show that given any configuration of the ring, either (1) no other machine has the same label as the bottom, or (2) there exists a label that is different from all machines. We show that if condition (1) does not hold, then condition (2) is true. If there exists a machine that has the same label as that of bottom, then there are now K – 1 labels left to be distributed among N – 2 machines. Since K ≥ N, we see that there is some label which is not used.

Furthermore, within a finite number of moves, condition (1) will be true. Note that if some label is missing from the network, it can be generated only by the bottom machine. Moreover, the bottom machine simply cycles among all labels. Since the bottom machine moves after some finite number of moves by normal machines, the bottom machine will eventually get the missing label.

We now show that if the system is in an illegal state, then within O(N²) moves, it reaches a legal state. It is easy to see that once the bottom machine gets the unique label, the system stabilizes in O(N²) moves. The bottom machine can move at most N times before it acquires the missing label. Machine 1 therefore can move at most N + 1 times before the bottom acquires the label. Similarly, machine i can move at most N + 1 times before the bottom gets the label. By adding up all the moves, we get N + (N + 1) + . . . + (N + N – 1) = O(N²) moves.

In this algorithm, the processes could read the state of their left neighbors. How do we implement this in a distributed system? One possibility is for a machine to periodically query its left neighbor. However, this may generate a lot of messages in the network. A more message-efficient solution is for a token to go around the system. The token carries with it the state of the last machine that it visited. But now we have to worry about the token getting lost and the presence of multiple tokens in the system. To guard against the token getting lost, we will require the bottom machine to generate a new token if it does not see a token in a certain timeout interval. To accomplish this, we use the following Java object as a periodic task. On invocation, this task sends a restart message to the bottom machine. To handle this message, the bottom machine calls the sendToken method.

import java. util. TimerTask;
public class RestartTask extends TimerTask {
        MsgHandler app;
        public RestartTask (MsgHandler app) {
                this.app = app;
        }
        public void run() {
                app. handleMsg(null, 0, "restart ");
        }
}

We use a boolean tokenSent to record if the token has been sent by the bottom machine in the last timeout interval. If not, a token is sent out.

Multiple tokens do not pose any problem in this scheme because that only means that multiple processes will read the state of their left neighbors. The algorithm is shown in Figure 18.4 for the bottom machine and in Figure 18.5 for the normal machine.

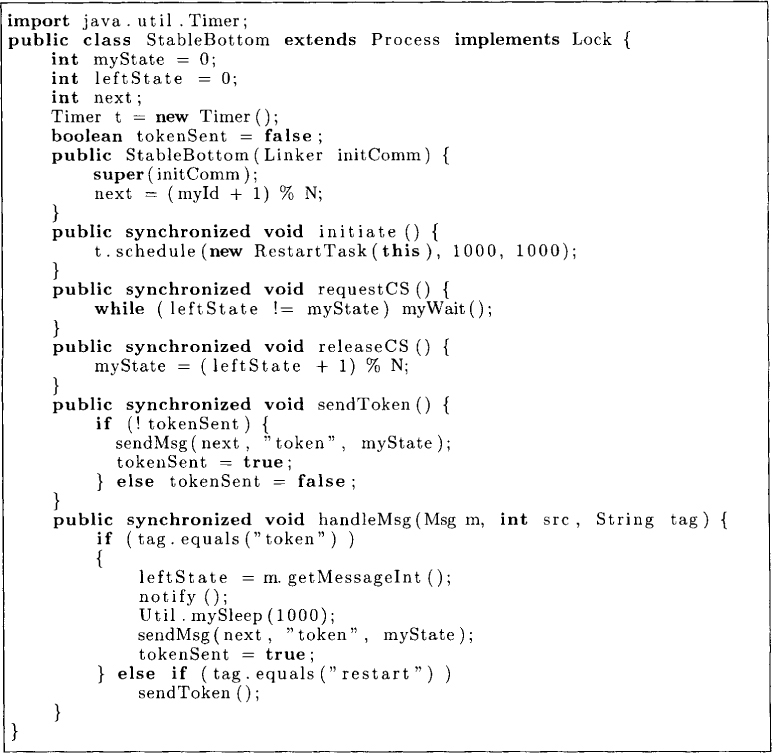
Figure 18.4: Self-stabilizing algorithm for mutual exclusion in a ring for the bottom machine

Figure 18.5: Self-stabilizing algorithm for mutual exclusion in a ring for a normal machine

18.3 Self-Stabilizing Spanning Tree Construction

Assume that the underlying topology of a communication network is a connected undirected graph. Furthermore, one of the node is a distinguished node called root. Our task is to design a self-stabilizing algorithm to maintain a spanning tree rooted at the given node. Note that determining parent pointers of the spanning tree once is not enough. Any data fault can corrupt these pointers. We would need to recalculate parent pointers periodically. To calculate the parent pointers, we also use a variable dist that indicates the distance of that node from the root.

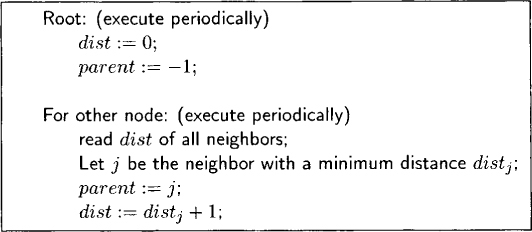
Figure 18.6: Self-stabilizing algorithm for (BFS) spanning tree

The algorithm shown in Figure 18.6 is quite simple. In this version, we assume that a node can read the value of variables of its neighbors. Later, we will translate this program into a distributed program. Each node maintains only two variables— parent and dist. The root node periodically sets parent to –1 and dist to 0. If any of these values get corrupted, the root node will reset it to the correct value by this mechanism. A nonroot node periodically reads the variable dist of all its neighbors. It chooses the neighbor with the least distance and makes that neighbor its parent. It also sets its own distance to one more than the distance of that neighbor.

It is easy to verify that no matter what the values of parent and dist initially are, the program eventually converges to valid values of parent and dist.

Let us now translate this program into a distributed program. The program for the root node shown in Figure 18.7 is identical to that in Figure 18.6. For periodic recalculation we use a timer that schedules RestartTask after a fixed time interval.

The algorithm for a nonroot node is shown in Figure 18.8. A nonroot node reads the values of the neighboring nodes by sending them a query message of type Q.dist. Whenever a node receives a message of type Q.dist it responds with a message of type A. dist with the value of its dist variable. The variable numReports indicate the number of A.dist messages that node is expecting. Whenever numReports become 0, it knows that it has heard from all its neighbors and therefore it knows the neighbor with the least distance. The variable newDist is used for recalculation of the distance.

The main program that invokes StableSpanRoot and StableSpanNonroot is shown in Figure 18.9.

Figure 18.7: Self-stabilizing spanning tree algorithm for the root

18.4 Problems

  18.1. Show that a system with four machines may not stabilize if it uses the K-state machine algorithm with K = 2.

  18.2. Show that the K-state machine algorithm converges to a legal state in at most O(N²) moves by providing a norm function on the configuration of the ring that is at most O(N²)), decreases by at least 1 for each move, and is always nonnegative.

Figure 18.8: Self-stabilizing spanning tree algorithm for nonroot nodes

Figure 18.9: A Java program for spanning tree

  18.3. In our K-state machine algorithm we have assumed that a machine can read the value of the state of its left machine and write its own state in one atomic action. Give a self-stabilizing algorithm in which a processor can only read a remote value or write a local value in one step, but not both.

*18.4. (due to Dijkstra [Dij74]) Show that the following four-state machine algorithm is self-stabilizing. The state of each machine is represented by two booleans xS and upS. For the bottom machine upS = true and for the top machine upS = false always hold.

Bottom:

if (xS = xR) and ¬upR then xS := ¬xS;

Normal:

if xS ≠ xL then xS := ¬xS; upS := true;
if xS = xR and upS and ¬upR then upS := false;

Top:

if (xS ≠ xL) then xS := ¬xS;

*18.5. Assume that each process P_i has a pointer that is either null or points to one of its neighbors. Give a self-stabilizing, distributed algorithm on a network of processes that guarantees that the system reaches a configuration where (a) if P_i points to P_j, then P_j points to P_i, and (b) there are no two neighboring processes such that both have null pointers.

18.5 Bibliographic Remarks

The idea of self-stabilizing algorithms first appeared in a paper by Dijkstra [Dij74], where three self-stabilizing algorithms were presented for mutual exclusion in a ring.