Chapter 13

Leader Election

13.1 Introduction

Many distributed systems superimpose a logical ring topology on the underlying network to execute control functions. An important control function is that of electing a leader process. The leader can serve as a coordinator for centralized algorithms for problems such as mutual exclusion. Electing a leader in a ring can also be viewed as the problem of breaking symmetry in a system. For example, once a deadlock is detected in the form of a cycle, we may wish to remove one of the nodes in the cycle to remove the deadlock. This can be achieved by electing the leader.

We abstract the leader election problem using the interface Election shown below.

public interface Election extends MsgHandler {
      void startElection ();
      int getLeader ();//blocks till the leader is known
}

Any implementation of Election should provide the method startElection, which is invoked by one or more processes in the system. The method getLeader returns the identity of the leader. If the identity of the leader is not known, then this method blocks until the leader is elected.

The leader election problem is similar to the mutual exclusion problem discussed in Chapter 8. In both problems, we are interested in choosing one of the processes as a privileged process. Coordinator-based or token-based solutions for mutual exclusion are not applicable for the leader election problem, because deciding which process can serve as the coordinator or has the token is precisely the leader election problem. If processes have unique identifiers and the underlying communication network is completely connected, then we can apply Lamport’s mutual exclusion algorithm to determine the leader—the first process to enter the critical section is deemed as the leader. However, this algorithm requires every process to communicate with every other process in the worst case. We will explore more efficient algorithms for the ring topology.

13.2 Ring-Based Algorithms

A ring is considered anonymous if processes in the ring do not have unique identifiers. Furthermore, every process has an identical state machine with the same initial state.

It is not difficult to see that there is no deterministic algorithm for leader election in an anonymous ring. The reason is that we have complete symmetry initially—no process is distinguishable from other processes. Because there is a unique leader, we know that the system can never terminate in a symmetric state. Thus the algorithm has not terminated in the initial state. We now show an execution that moves the system from one symmetric state to the other. Assume that any process in the ring takes a step. By symmetry, this step is possible at all processes. Thus in the adversarial execution all processes take the same step. Since the algorithm is deterministic, the system must again reach a symmetric state. Therefore, the system could not have terminated (i.e., the leader could not have been elected yet). We can repeat this procedure forever.

Observe that our argument uses the fact that the algorithm is deterministic. A randomized algorithm can solve the leader election problem in expected finite time (see Problem 13.1).

13.2.1 Chang-Roberts Algorithm

Now assume that each process has a unique identifier. In such a system, a leader can be elected in a ring by a very simple algorithm due to Chang and Roberts. The algorithm ensures that the process with the maximum identifier gets elected as the leader. In the algorithm shown in Figure 13.1, every process sends messages only to its left neighbor and receives messages from its right neighbor. A process can send an election message along with its identifier to its left, if it has not seen any message with a higher identifier than its own identifier. It also forwards any message that has an identifier greater than its own; otherwise, it swallows that message. If a process receives its own message, then it declares itself as the leader by sending a leader message. When a process receives its own leader message, it knows that everybody knows the leader.

In the algorithm, one or more processes may spontaneously wake up and initiate the election using the method startElection. When a process wakes up on receiving a message from a process with a smaller identifier, it circulates its own election message.

Note that the algorithm does not require any process to know the total number of processes in the system.

Figure 13.1: The leader election algorithm

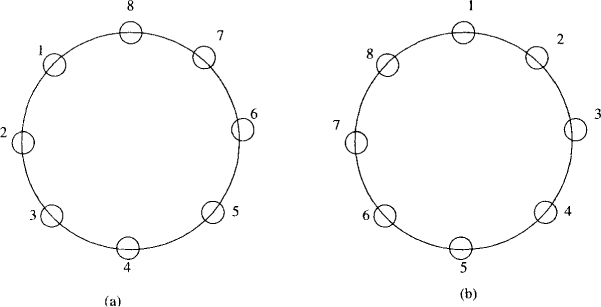
Figure 13.2: Configurations for the worst case (a) and the best case (b)

The worst case of this algorithm is when N processes with identifiers 1 . . . N are arranged clockwise in decreasing order (see Figure 13.2(a)). The message initiated by process j will travel j processes before it is swallowed by a larger process. Thus the total number of election messages in the worst case is

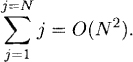
In addition, there are N leader messages. The best case is when the same identifiers are arranged clockwise in the increasing order. In that case, only O(N) election messages are required. On an average, the algorithm requires O(N log N ) messages (see Problem 13.2).

13.2.2 Hirschberg-Sinclair Algorithm

In this section we assume that the ring is bidirectional so that messages can be sent to the left or the right neighbor. The main idea of the algorithm is to carry out elections on increasingly larger sets. The algorithm works in asynchronous rounds such that a process P_i tries to elect itself in round r. Only processes that win their election in round r can proceed to round r + 1. The invariant satisfied by the algorithm is that process P_i is a leader in round r iff P_i has the largest identifier of all nodes that are at distance 2^r or less from P_i. It follows that any two leaders after round r must be at least 2^r distance apart. In other words, after round r, there are at most N/(2^r–1 + 1) leaders. With each round, the number of leaders decreases, and in O(log N) rounds there is exactly one leader. It can be shown by using induction that there are at most O(N) messages per round, which gives us a bound of O(N log N). The details of the algorithm and its proof of correctness are left as exercises.

13.3 Election on General Graphs

First assume that the graph is completely connected, that is, every process can talk to every other process directly. In this case, we can modify Lamport’s mutual exclusion algorithm for leader election. One or more processes start the election. Any process that enters the critical section first is considered the leader.

Note that a process need not acknowledge another process’s request if it knows that there is a request with a lower timestamp. Moreover, there is no need for release messages for the leader election problem. As soon as a process enters the critical section, it can inform all other processes that it has won the election. If c processes start the election concurrently, then this algorithm takes at most 2cN messages for “request” and “acknowledgment,” and N messages for the final broadcast of who the leader is.

Now consider the case when the graph is not completely connected. We assume that every process initially knows only the identities of its neighbors. In this case, we can simulate the broadcast from a node v by constructing a spanning tree rooted at v.

13.3.1 Spanning Tree Construction

We assume that there is a distinguished process root. Later we will remove this assumption. The algorithm shown in Figure 13.3 is initiated by the root process by sending an invite message to all its neighbors. Whenever a process P_i receives an invite message (from P_j) for the first time, it sends that message to all its neighbors except P_j. To P_j it sends an accept message, indicating that P_j is the parent of P_i. If P_i receives an invite message from some other process thereafter, it simply replies with a reject message. Every node keeps a count of the number of nodes from which it has received messages in the variable numreports. When this value reaches the total number of neighbors, P_i knows that it has heard from all processes that it had sent the invite message (all neighbors except the parent). At this point, P_i can be sure that it knows all its children and can halt.

This algorithm is also called the flooding algorithm because it can be used to broadcast a message m, when there is no predefined spanning tree. The algorithm for flooding a message is simple. Whenever a process P_i receives a message m (from P_j) for the first time, it sends that message to all its neighbors except P_j.

Figure 13.3: A spanning tree construction algorithm

What if there is no distinguished process? We assume that each process has a unique id, but initially every process knows only its own id. In this case, each node can start the spanning tree construction assuming that it is the distinguished process. Thus many instances of spanning tree construction may be active concurrently. To distinguish these instances, all messages in the spanning tree started by P_i contain the id for P_i. By ensuring that only the instance started by the process with the largest id succeeds, we can build a spanning tree even when there is no distinguished process. The details of the algorithm are left as an exercise.

13.4 Application: Computing Global Functions

One of the fundamental difficulties of distributed computing is that no process has access to the global state. This difficulty can be alleviated by developing mechanisms to compute functions of the global state. We call such functions global functions. More concretely, assume that we have x_i located at process P_i. Our aim is to compute a function f(x₁, x₂,. . . , x_N) that depends on states of all processes.

First, we present an algorithm for convergecast and broadcast on a network, assuming that there is a predefined spanning tree. The convergecast requires information from all nodes of the tree to be collected at the root of the tree. Once all the information is present at the root node, it can compute the global function and then broadcast the value to all nodes in the tree. Both the convergecast and the broadcast require a spanning tree on the network.

The algorithms for convergecast and broadcast are very simple if we assume a rooted spanning tree. For convergecast, the algorithm is shown in Figure 13.4. Each node in the spanning tree is responsible to report to its parent the information of its subtree. The variable parent, for a node x, is the identity of the neighbor of x, which is the parent in the rooted spanning tree. For the root, this value is null. The variable numchildren keeps track of the total number of its children, and numreports keeps track of the number of its children who have reported. When the root node hears from all its children, it has all the information needed to compute the global function.

The broadcast algorithm shown in Figure 13.5 is dual of the convergecast algorithm. The algorithm is initiated by the root process by sending the broadcast message to all its children. In this algorithm, messages traverse down the tree.

We now combine the convergecast and the broadcast algorithms to provide a service that can compute a global function. For simplicity, we assume that the global function is commutative and associative, such as min, max, sum, and product. This allows internal nodes to send intermediate results to the parent node during the convergecast process. The GlobalService interface is shown below.

Figure 13.4: A convergecast algorithm

Figure 13.5: A broadcast algorithm

public interface GlobalService extends MsgHandler {
        public void initialize (int x, FuneUser prog);
        public int computeGloba1 ();
}

Any program that wants to compute a global function can invoke computeGlobal with its value and the global function to be computed as arguments. The FuncUser is required to have a binary function called func as shown below.

public interface FuncUser {
    public int func(int x, int y);
}

Now we can give an implementation for GlobalService based on the ideas of convergecast and broadcast. The Java implementation is shown in Figure 13.6.

The program uses two types of messages, subTreeVal and globalFunc, for convergecast and broadcast respectively. The list pending keeps track of all the children that have not reported using the subTree Val message. Whenever a sub Tree Val message is received, it is combined with myValue using prog.func(). Whenever the pending list becomes empty, that node has the value of the global function for its subtree. If the node is a root, it can initiate the broadcast; otherwise it sends its myValue to its parent and waits for the globalFunc message to arrive. The final answer is given by the value that comes with this message.

The class GlobalFunc can be used to compute a global function as illustrated by the class GlobalFuncTest in Figure 13.7.

13.5 Problems

13.1. An algorithm on a ring is considered nonuniform if every process knows the total number of processes in the ring. Show that there exists a randomized nonuniform algorithm to elect a leader on an anonymous ring that terminates with probability 1. (Hint: Consider an algorithm with rounds in which initially all processes are eligible. In each round, an eligible process draws at random from 0. . . m (where m > 0). The subset of processes that draw the maximum element from the set selected is eligible for the next round. If there is exactly one eligible process, then the algorithm terminates. Analyze the expected number of rounds as a function of N and m.]

13.2. Show that the Chang Roberts algorithm requires O(N log N) messages on average.

13.3. Modify the Chang—Roberts algorithm such that a process keeps track of maxid, the largest identifier it has seen so far. It swallows any message with any identifier that is smaller than maxid. What are the worst and the expected number of messages for this variant of the algorithm?

13.4. Give an O(N log N) algorithm for leader election on a bidirectional ring.

Figure 13.6: Algorithm for computing a global function

Figure 13.7: Computing the global sum

13.6 Bibliographic Remarks

The impossibility result on anonymous rings is due to Angluin [Ang80]. The O(N²) algorithm is due to Chang and Roberts [CR79]. The O(N log N) algorithm discussed in the chapter is due to Hirschberg and Sinclair [HS80]. Dolev, Klawe and Rodeh [DKR82] and Peterson [Pet82] have presented an O(N log N) algorithm for unidirectional rings. For lower bounds of Ω(N log N), see papers by Burns [Bur80] and Pachl, Korach, and Rotem [PKR82].