Chapter 4
Consistency Conditions
4.1 Introduction
In the presence of concurrency, one needs to revisit the correctness conditions of executions, specifically, which behaviors are correct when multiple processes invoke methods concurrently on a shared object. Let us define a concurrent object as one that allows multiple processes to execute its operations concurrently. For example, a concurrent queue in a shared memory system may allow multiple processes to invoke enqueue and dequeue operations. The natural question, then, is to define which behavior of the object under concurrent operations is consistent (or correct). Consider the case when a process P enqueues x in an empty queue. Then it calls the method dequeue, while process Q concurrently enqueues y. Is the queue’s behavior acceptable if process P gets y as the result of dequeue? The objective of this chapter is to clarify such questions.
The notion of consistency is also required when objects are replicated in a parallel or a distributed system. There are two reasons for replicating objects: fault tolerance and efficiency. If an object has multiple copies and a processor that contains one of the copies of the object goes down, the system may still be able to function correctly by using other copies. Further, accessing a remote object may incur a large overhead because of communication delays. Suppose that we knew that most accesses of the object are for read only. In this case, it may be better to replicate that object. A process can read the value from the replica that is closest to it in the system. Of course, when we perform a write on this object, we have to worry about consistency of data. This again requires us to define data consistency. Observe that any system that uses caches, such as a multiprocessor system, also has to grapple with similar issues.
4.2 System Model
A concurrent system consists of a set of sequential processes that communicate through concurrent objects. Each object has a name and a type. The type defines the set of possible values for objects of this type and the set of primitive operations that provide the only means to manipulate objects of this type. Execution of an operation takes some time; this is modeled by two events, namely, an invocation event and a response event. Let op(arg) be an operation on object x issued at P; arg and res denote op’s input and output parameters, respectively. Invocation and response events inv(op(arg)) on x at P and resp(op(res)) from x at P will be abbreviated as inv(op) and resp(op) when parameters, object name, and process identity are not necessary. For any operation e, we use proc(e) to denote the process and object(e) to denote the set of objects associated with the operation. In this chapter, we assume that all operations are applied by a single process on a single object. In the problem set, we explore generalizations to operations that span multiple objects.
A history is an execution of a concurrent system modeled by a directed acyclic graph (H, <H), where H is the set of operations and <H is an irreflexive transitive relation that captures the occurred before relation between operations. Sometimes we simply use H to denote the history when <H is clear from the context. Formally, for any two operations e and f:
e <H f if resp(e) occurred before inv(f) in real time.
Observe that this relation includes the following relations:
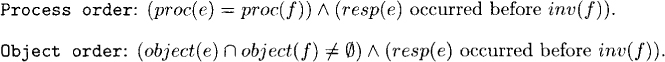
A process subhistory H|P (H at P) of a history H is a sequence of all those events e in H such that proc(e) = P. An object subhistory is defined in a similar way for an object x, denoted by H|x (H at x). Two histories are equivalent if they are composed of exactly the same set of invocation and response events.
A history (H, <H) is a sequential history if <H is a total order. Such a history would happen if there was only one sequential process in the system. A sequential history is legal if it meets the sequential specification of all the objects. For example, if we are considering a read-write register x as a shared object, then a sequential history is legal if for every read operation that returns its value as v, there exists a write on that object with value v, and there does not exist another write operation on that object with a different value between the write and the read operations. For a sequential queue, if the queue is nonempty then a dequeue operation should return the item that was enqueued earliest and has not been already dequeued. If the queue is empty, then the dequeue operation should return null.
Our goal is to determine whether a given concurrent history is correct.
4.3 Sequential Consistency
Definition 4.1 (Sequentially Consistent) A history (H, <H) is sequentially consistent if there exists a sequential history S equivalent to H such that S is legal and it satisfies process order.
Thus a history is sequentially consistent if its execution is equivalent to a legal sequential execution and each process behavior is identical in the concurrent and sequential execution. In the following histories, P, Q, and R are processes operating on shared registers x, y, and z. We assume that all registers have 0 initially. The response of a read operation is denoted by ok(v), where v is the value returned, and the response of a write operation is denoted by ok(). The histories are shown graphically in Figure 4.1.
1. H1 = P write(x, 1), Q read(x), Q ok(0), P ok().
Note that H1 is a concurrent history. Q invokes the read(x) operation before the write(x, 1) operation is finished. Thus write(x, 1) and read(x) are concurrent operations in H1. H1 is sequentially consistent because it is equivalent to the following legal sequential history.
S = Q read(x), Q ok(0), P write(x, 1), P ok().
To see the equivalence, note that
H1|P = S|P = P write(x, 1), P ok().
H1|Q = S|Q = Q read(x), Q ok(0).
2. H2 = P write(x, 1), P ok(), Q read(x), Q ok(0).
Somewhat surprisingly, H2 is also sequentially consistent. Even though P got the response of its write before Q, it is okay for Q to have read an old value. Note that H2 is a sequential history but not legal. However, it is equivalent to the following legal sequential history:
Q read(x), Q ok(0), P write(x, 1), P ok().
3. H3 = P write(x, 1), Q read(x), P ok(), Q ok(0), P read(x), P ok(0).
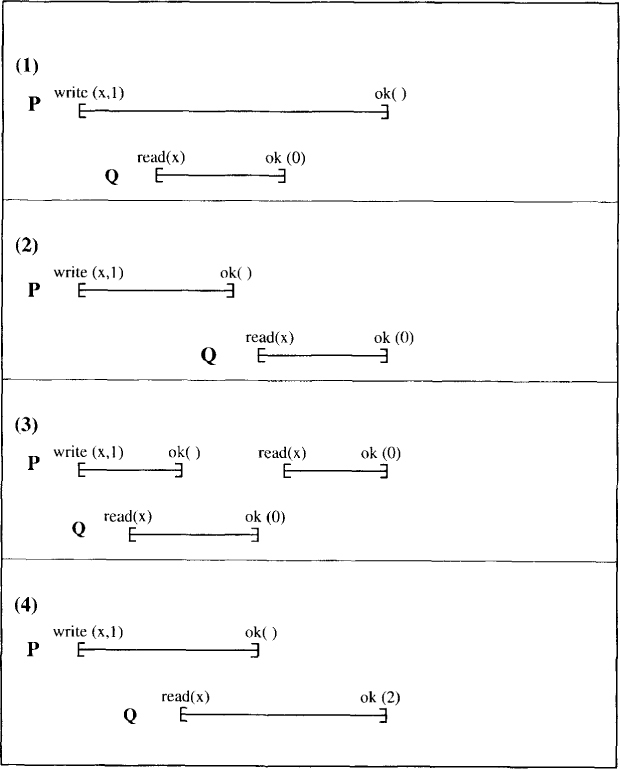
Figure 4.1: Concurrent histories illustrating sequential consistency
H3 is not sequentially consistent. Any sequential history equivalent to H3 must preserve process order. Thus the read operation by P must come after the write operation. This implies that the read cannot return 0.
4. H4 = P write(x, 1), Q read(x), P ok(), Q ok(2).
H4 is also not sequentially consistent. There is no legal sequential history equivalent to H4 because the read by Q returns 2, which was never written on the register (and was not the initial value).
4.4 Linearizability
Linearizability is a stronger consistency condition than sequential consistency. Intuitively, an execution of a concurrent system is linearizable if it could appear to an external observer as a sequence composed of the operations invoked by processes that respect object specifications and real-time precedence ordering on operations. So, linearizability provides the illusion that each operation on shared objects issued by concurrent processes takes effect instantaneously at some point between the beginning and the end of its execution. Formally, this is stated as follows.
Definition 4.2 (Linearizable) A history (H, <H) is linearizable if there exists a sequential history (S, <) equivalent to H such that S is legal and it preserves <H.
Since <H includes process order, it follows that a linearizable history is always sequentially consistent. Let us reexamine some histories that we saw earlier.
1. H1 = P write(x, 1), Q read(x), Q ok(0), P ok().
H1 is linearizable because the following legal sequential history,
Q read(x), Q ok(0), P write(x, 1), P ok()
preserves <H.
2. H2 = P write(x, 1), P ok(), Q read(x), Q ok(0).
H2 is sequentially consistent but not linearizable. The legal sequential history used for showing sequential consistency does not preserve <H.
A key advantage of linearizability is that it is a local property, that is, if for all objects x, H|x is linearizable, then H is linearizable. Sequential consistency does not have this property. For example, consider two concurrent queues, s and t. Process P enqueues x in s and t. Process Q enqueues y in t and then in s. Now P gets y from deq on s and Q get x when it does deq on t.
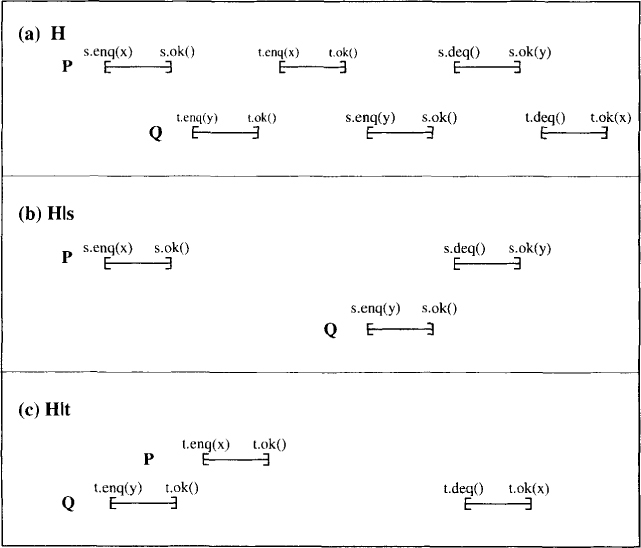
Figure 4.2: Sequential consistency does not satisfy locality
Consider the following histories shown in Figure 4.2:
H =
P s.enq(x), P s.ok(),
Q t.enq(y), Q t.ok(),
P t.enq(x), P t.ok(),
Q s.enq(y), Q s.ok(),
P s.deq(), P s.ok(y),
Q t.deq(), Q t.ok(x),
H|s =
P s.enq(x), P s.ok(),
Q s.enq(y), Q s.ok(),
P s.deq(), P s.ok(y).
H|t =
Q t.enq(y), Q t.ok(),
P t.enq(x), P t.ok(),
Q t.deq(), Q t.ok(x)
Both H|s and H|t are sequentially consistent but H is not.
To see that the linearizability is a local property, assume that (Sx, <x) is a linearization of H|x, that is, (Sx, <x) is a sequential history that is equivalent to H|x. We construct an acyclic graph that orders all operations on any object and also preserves occurred before order <H. Any sort of this graph will then serve as a linearization of H. The graph is constructed as follows. The vertices are all the operations. The edges are all the edges given by union of all <x and <H. This graph totally orders all operations on any object. Moreover, it preserves <H. The only thing that remains to be shown is that it is acyclic. Since <x are acyclic, it follows that any cycle, if it exists, must involve at least two objects.
We will show that cycle in this graph implies a cycle in <H. If any two consecutive edges in the cycle are due to just <x or just <H, then they can be combined due to transitivity. Note that e <x f <y g for distinct objects x and y is not possible because all operations are unary (e <x f <y g implies that f operates on both x and y). Now consider any sequence of edges such that e <H f <x g <H h.
e <H f implies res(e) precedes inv(f) { definition of <H }
f <x g implies inv(f) precedes res(g) { <x is a total order }
g <H h implies res(g) precedes inv(h) { definition of <H }.
These relations can be combined to give that res(e) precedes inv(h). Therefore, e <H h. Thus any cycle in the graph can be reduced to a cycle in <H, a contradiction because <H is irreflexive.
So far we have only looked at consistency conditions for complete histories, that is, histories in which every invocation operation has a corresponding response operation. We can generalize the consistency conditions for partial histories as follows. A partial history H is linearizable if there exists a way of completing the history by appending response events such that the complete history is linearizable. For example, consider the following history:
H3 = P write(x, 1), Q read(x), Q ok(0)
H3 is linearizable because
P write(x, 1), Q read(x), Q ok(0), P ok()
is linearizable. This generalization allows us to deal with systems in which some processes may fail and consequently some response operations may be missing.
4.5 Other Consistency Conditions
Although we have focused on sequential consistency and linearizability, there are many consistency conditions that are weaker than sequential consistency. A weaker consistency condition allows more efficient implementation at the expense of increased work by the programmer, who has to ensure that the application works correctly despite weaker consistency conditions.
Consider a program consisting of two processes, P and Q, with two shared variables x and y. Assume that the initial values of x and y are both 0. P writes 1 in x and then reads the value of y; Q writes 1 in y and then reads the value of x. Strong consistency conditions such as sequential consistency or linearizability prohibit the results of both reads from being 0. However, if we assume that the minimum possible time to read plus the minimum possible time to write is less than the communication latency, then both reads must return 0. The latency is the information delivery time, and each processor cannot possibly know of the events that have transpired at the other processor. So, no matter what the protocol is, if it implements sequential consistency, it must be slow.
Causal consistency is weaker than sequential consistency. Causal consistency allows for implementation of read and write operations in a distributed environment that do not always incur communication delay; that is, causal consistency allows for cheap read and write operations.
With sequential consistency, all processes agree on the same legal sequential history S. The agreement defined by causal consistency is weaker. Given a history H, it is not required that two processes P and Q agree on the same ordering for the write operations, which are not ordered in H. The reads are, however, required to be legal. Each process considers only those operations that can affect it, that is, its own operations and only write operations from other processes. Formally, for read-write objects causal consistency can be defined as follows.
Definition 4.3 (Causally Consistent) A history (H, <H) is causally consistent if for each process Pi, there is a legal sequential history (Si, <Si) where Si is the set of all operations of Pi and all write operations in H, and <Si, respects the following order:
Process order: If Pi performs operation e before f, then e is ordered before f in Si.
Object order: If any process P performs a write on an object x with value v and another process Q reads that value v, then the write by P is ordered before read by Q in Si.
Intuitively, causal consistency requires that causally related writes be seen by all processes in the same order. The concurrent writes may be seen in different order by different processes.
It can be proved that sequential consistency implies causal consistency but the converse does not hold. As an example, consider history H1 in which P1 does w1(x, 1), r1(x, 2) and P2 does w2(x, 2), r2(x, 1).
The history is causally consistent because the following serializations exist:
S1 = w1(x, 1), w2(x, 2), r1(x, 2)
S2 = w2(x, 2), w1(x, 1), r2(x, 1)
Thus we require only that there is a legal sequential history for every process and not one for the entire system. P1 orders w1 before w2 in S1 and P2 orders w2 before w1 but that is considered causally consistent because w1 and w2 are concurrent writes. It can be easily proved that history H1 is not sequentially consistent.
The following history is not even causally consistent. Assume that the initial value of x is 0. The history at process P is
H|P = P r(x, 4), P w(x, 3).
The history at process Q is
H|Q = Q r(x, 3), Q w(x, 4).
Since Q reads the value 3 and then writes the value of x, the write by Q should be ordered after the write by P. P’s read is ordered before its write; therefore, it cannot return 4 in a causally consistent history.
The table in Figure 4.3 summarizes the requirements of all consistency conditions considered in this chapter. The second column tells us whether the equivalent legal history required for the consistency condition is global. The third column tells us the requirement on the legal history in terms of the order preserved. For example, linearizability requires that there be a single equivalent legal history that preserves the occurred before order.

Figure 4.3: Summary of consistency conditions
4.6 Problems
4.1. Consider a concurrent stack. Which of the following histories are linearizable? Which of the them are sequentially consistent? Justify your answer.
(a) P push(x), P ok(), Q push(y), Q ok(), P pop(), P ok(x)
(b) P push(x), Q push(y), P ok(), Q ok(), Q pop(), Q ok(x)
4.2. Assume that all processors in the system maintain a cache of a subset of objects accessed by that processor. Give an algorithm that guarantees sequential consistency of reads and writes of the objects.
4.3. Assume that you have an implementation of a concurrent system that guarantees causal consistency. Show that if you ensure that the system does not have any concurrent writes, then the system also ensures sequential consistency.
4.4. FIFO consistency requires that the writes done by the same process be seen in the same order. Writes done by different processes may be seen in different order. Show a history that is FIFO-consistent but not causally consistent.
4.5. Given a poset (H, <H) denoting a system execution, we define a relation → H as the transitive closure of union of process and object order. We call (H, <H) normal if there exists an equivalent sequential history that preserves → H. Show that when all operations are unary, a history is linearizable iff it is normal.
4.6. Consider the following history of six events in which operations span multiple objects, assuming that A and B are initialized to 0:

Show that this history is not linearizable but normal.
*4.7. Assume that every message delay is in the range [d – u, d] for 0 < u < d. Show that in any system that ensures sequential consistency of read-write objects, the sum of delays for a read operation and a write operation is at least d.
*4.8. (due to Taylor [Tay83]) Show that the problem of determining whether (H, <H) is sequentially consistent for read-write registers is NP-complete.
*4.9. (due to Mittal and Garg [MG98]) Generalize the definition of sequential consistency and linearizability for the model in which operations span multiple objects. Give distributed algorithms to ensure sequential consistency and linearizability in this model.
4.7 Bibliographic Remarks
Sequential consistency was first proposed by Lamport [Lam79]. The notion of linearizability for read/write registers was also introduced by Lamport [Lam86] under the name of atomicity. The concept was generalized to arbitrary data types and termed as linearizability by Herlihy and Wing [HW90]. Causal consistency was introduced by Hutto and Ahamad [HA90].
