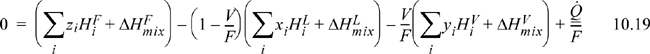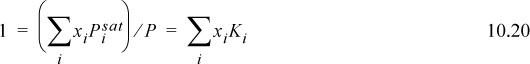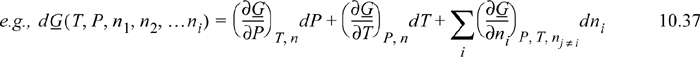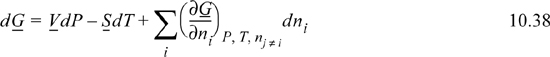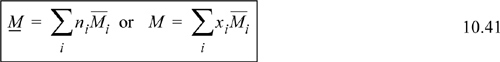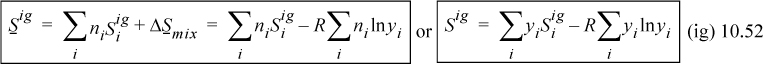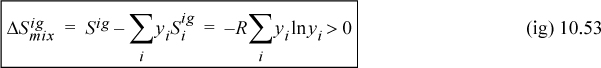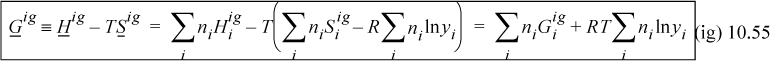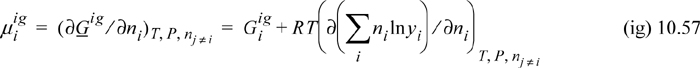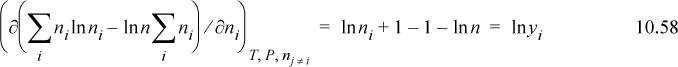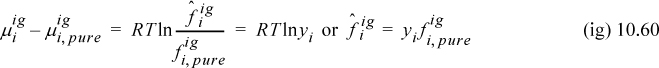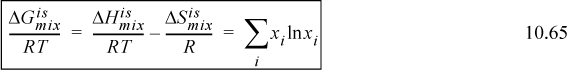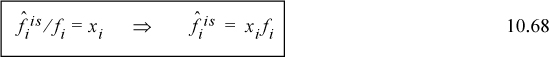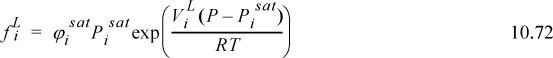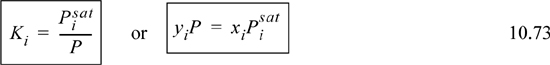Chapter 10. Introduction to Multicomponent Systems
What we obtain too cheap we esteem too lightly.
Thomas Paine
Superficially, the extension of pure component concepts to mixtures may seem simple. In fact, this is a significant problem of modern science that impacts phase transitions in semi- and superconductors, polymer solutions and blends, alloy materials, composites, and biochemistry. Specialists in each of these areas devote considerable effort to the basic problem of segmental interactions between molecules. From a thermodynamic perspective, these various research efforts are very similar. The specific types of molecules differ, and the pair potential models may be different, but the means of connecting the molecular scale to the macro scale remains the same.
Our coverage of multicomponent systems consists of (1) a very brief extension to mixtures of the mathematical and physical principles; and (2) an introductory description of several common methods for reducing these principles to practice. This description is merely introductory because learning the specific details is partially what distinguishes the polymer scientist from the ceramicist. Such specialized study is greatly facilitated by having an appreciation of the types of molecular interactions that are most influential in each situation. Of similar importance is the ability to analyze thermodynamic data such that key aspects of processes are easily ascertained.
Chapter Objectives: You Should Be Able to...
1. Interpret phase diagrams to locate dew, bubble, and flash conditions. Use the lever rule in two-phase regions.
2. Identify when a bubble, dew, or flash computation is required and perform the computation subject to the assumptions of an ideal solution.
3. Know the assumptions of an ideal solution and where to start with the fundamental equations to develop models of nonideal solutions.
4. Recognize when the ideal solution model is reasonable and when it is not, including comparisons of theoretical results to experimental data, graphically and statistically, coupled with conceptual reasoning about the nature of the molecular interactions.
5. Understand how VLE relates conceptually to the process of distillation.
10.1. Introduction to Phase Diagrams
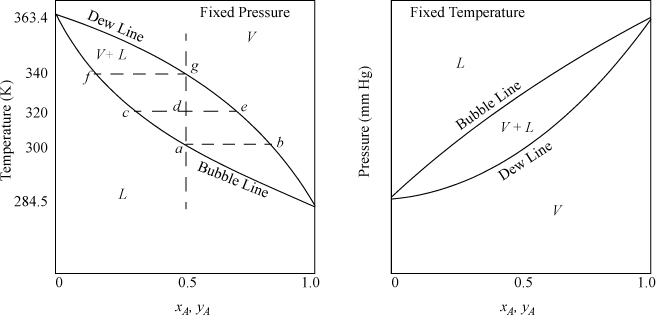
Before we delve into the details of calculating phase equilibria, let us introduce elementary concepts of common vapor-liquid phase diagrams. For a pure fluid, the Gibbs phase rule shows vapor-liquid equilibrium occurs with only one degree of freedom, F = C – P + 2 = 1 – 2 + 2 = 1. At one atmosphere pressure, vapor-liquid equilibria will occur at only one temperature—the normal boiling point temperature. However, with a binary mixture, there are two degrees of freedom, F = 2 – 2 + 2 = 2. For a system with fixed pressure, phase compositions and temperature can both be varied over a finite range when two phases coexist. Experimental data for experiments of this type are usually presented as a function of T and composition on a plot known as a T-x-y diagram, such as that shown qualitatively in Fig. 10.1. At fixed temperature, pressure and composition may vary in a binary mixture and obtain data to create a P-x-y diagram as shown also in Fig. 10.1. The region where two phases coexist is shown by the area enclosed by the curved lines on either plot and is known as the phase envelope.1 On the T-x-y diagram, the vapor region is at the top (raising T at fixed P causes vaporization of liquid). On the P-x-y diagram, the vapor region is at the bottom (lowering P at fixed T causes vaporization of liquid). Note that the intersections of the phase envelope with the ordinate scales at the pure component compositions give the pure component saturation temperatures on the T-x-y diagram, and the pure component vapor (saturation) pressures on the P-x-y diagram. Therefore, significant information about the shape of the diagram can often be deduced with a single mixture data point when combined with the pure component end points. Qualitatively, the shape of the P-x-y diagram can be found by inverting the T-x-y, and vice versa.2 Customarily, for binary systems in the separations literature, the more volatile component composition is plotted along the abscissa in mole fraction or percent.
Figure 10.1. Illustration of T-x-y (left) and P-x-y (right) diagrams.
The lower curve on the T-x-y diagram is next to the liquid region, and it is known as the bubble line. The bubble-temperature line gives the boiling temperature of the mixture as a function of composition at the specified pressure. The upper curve is next to the vapor region, and is known as the dew line. The two lines meet at the axes if the conditions are below the critical pressure of both components. At a given composition, the temperature along the bubble line is the temperature where an infinitesimal bubble of vapor coexists with liquid. Thus, at an over-all composition of 50 mole% A, the system of Fig. 10.1 at fixed pressure is 100% liquid below 300 K at the pressure of the diagram. As the temperature is raised, the overall composition is constrained to follow the vertical dashed line constructed on the diagram, and the first vapor bubble forms at the intersection of the bubble line at 300 K at point a, which is known as the bubble temperature for a 50 mole% mixture at the system pressure. Phase compositions at a given P and T may be found by reading the compositions from intersections of the bubble and dew lines with horizontal lines constructed on the diagram, such as the dashed line at 300 K. For our example at the bubble temperature, the liquid phase will be 50 mole% A because the first bubble of vapor has not yet caused a measurable change in the liquid composition. The vapor phase composition coexisting at the bubble-point temperature will be 80 mole% A (point b). As the temperature is increased to 320 K, the overall mixture is at point d, the liquid phase will be 30 mole% A (point c), and the vapor phase will be 70 mole% A (point e). Suppose we start an experiment with a 50 mole% mixture at 350 K, where the mixture is 100% vapor. As the temperature is lowered, the dew temperature is encountered at 340 K for the 50 mole% mixture at system pressure (point g), and the first drop of liquid is formed which is about 20 mole% A (point f). Note that the bubble and dew temperatures are composition-dependent. For example, the bubble temperature of a 30 mole% mixture is 320 K (point c), and the bubble temperature of a 20 mole% mixture is 340 K (point f). Similar discussion could be presented for the dew temperatures. The bubble and dew-point discussions could also be presented on the pressure diagram, but in this case we would refer to the bubble and dew pressures. Note that the relative vertical locations of the bubble- and dew lines are flipped on the two diagrams. The horizontal dotted lines connecting coexisting compositions are tie lines.
When we speak of composition in a two-phase mixture, we must be clear about which phase we are discussing. We use x to denote a liquid phase mole fraction, y to denote a vapor phase mole fraction, and z to denote an overall mole fraction.3 For the example, we have been discussing using a 50 mole% mixture: At the bubble point of 300 K we have zA = 0.5, xA = 0.5, yA = 0.8; at 320 K we have zA = 0.5, xA = 0.3, yA = 0.7; At 340 K we have zA = 0.5, xA = 0.20, yA = 0.5. At 320 K, the system is in the two-phase region, and we may use the compositions of the vapor and liquid phases, together with an overall mass balance, to calculate the fraction of the overall mixture that is vapor or liquid. This is known as a flash calculation. If the initial number of moles is denoted by F, and it separates into L moles of liquid and V moles of vapor, the overall mole balance is F = L + V, which can be written 1 = L/F + V/F. The A component balance is zAF = yAV + xAL, which can be written zA = yA · V/F + xA · L / F. Combining the two balances to eliminate V/F, the percentage that is liquid will be
which is simply given by line segment lengths, ![]() . Likewise the fraction that is vapor may be calculated
. Likewise the fraction that is vapor may be calculated
which is given by line segment lengths, ![]() . These balance equations are frequently called the lever rule. Note that the two fractions sum to one,
. These balance equations are frequently called the lever rule. Note that the two fractions sum to one, ![]() .
.
10.2. Vapor-Liquid Equilibrium (VLE) Calculations
Classes of VLE Calculations
Depending on the information provided, one may perform one of several types of vapor-liquid equilibrium (VLE) calculations to model the vapor-liquid partitioning. These are: bubble-point pressure (BP), dew-point pressure (DP), bubble-point temperature (BT), dew-point temperature (DT), and isothermal flash (FL) and adiabatic flash (FA). The specifications of the information required and the information to be computed are tabulated below in Table 10.1. Also shown in the table are indications of the relative difficulty of each calculation. The best approach to understanding the calculations is to gain experience by plotting phase envelopes in various situations.
Table 10.1. Summary of the Types of Phase Equilibria Calculations (This Table is Independent of the VLE Model)

![]() The classes of VLE calculations presented here will be used through the remainder of the text, so the concepts are extremely important.
The classes of VLE calculations presented here will be used through the remainder of the text, so the concepts are extremely important.
Principles of Calculations
Standard approaches to solving VLE problems utilize the ratio of vapor mole fraction to liquid mole fraction, known as the VLE K-ratio:
The information available from a physical situation is combined with the K-ratio using one of the procedures shown in Table 10.1. The information available is in the second column of the table. The procedure involves combination of the known information together with a model-dependent K-ratio to calculate an objective function based on the estimated unknown compositions. For a bubble calculation, all the xi are known, and we find the yi by solving for the condition where ![]() written in terms of xi, namely
written in terms of xi, namely ![]() . For dew calculations, all yi are known, and we solve for the condition where
. For dew calculations, all yi are known, and we solve for the condition where ![]() written in terms of yi and Ki. For a flash calculation, we solve for the condition where
written in terms of yi and Ki. For a flash calculation, we solve for the condition where ![]() written in terms of the overall mole fraction zi and Ki. The information in Table 10.1 is rigorous. The method used to calculate Ki is model-dependent and will be the focus of the next few chapters of the text. The Ki ratios generally vary with composition, pressure, and temperature, though we focus in this chapter on the use of Raoult’s law in situations where Ki ratios are dependent on only T and P.
written in terms of the overall mole fraction zi and Ki. The information in Table 10.1 is rigorous. The method used to calculate Ki is model-dependent and will be the focus of the next few chapters of the text. The Ki ratios generally vary with composition, pressure, and temperature, though we focus in this chapter on the use of Raoult’s law in situations where Ki ratios are dependent on only T and P.
Strategies for Solving VLE Problems
Note that there are only six different types of calculations for VLE summarized in Table 10.1. Usually the solution of the VLE problem will be relatively straightforward after deciding which row of the table to use. A crucial skill in solving VLE problems is interpreting the physical situation to decide which of the five methods should be used, and how to calculate the K-ratio.
1. Decide if the liquid, vapor, or overall composition is known from the problem statement.
2. Identify if the fluid is at a bubble or dew point. If the fluid is at a bubble point, the overall composition will be the same as the liquid composition. At the dew point, the overall composition will be the same as the vapor.
3. Identify if the P, T, or both P and T are fixed. Decide if the system is adiabatic.
4. The information collected in the first three steps can be used with the second column in Table 10.1 to identify the method.
5. Select a method to calculate the VLE K-ratio.
6. Decide if the method will be iterative, and if so, generate an initial guess for the solution. Approaches for handling iterative calculations are introduced in the following chapters and examples.
Iterative Calculations
When the K-ratios vary, VLE calculations require iterative solutions from an initial guess. For performing iterative calculations, useful aids include the Solver tool of Excel or the fzero() or fsolve() function of MATLAB. Many of the following examples summarize detailed calculations to illustrate fully the iterative procedure. In practice, the detailed calculations can be performed rapidly using a solver. Online supplements summarize the use of the iterative aids and the methods for successive substitution.
10.3. Binary VLE Using Raoult’s Law
For a small class of mixtures where the components have very similar molecular functionality and molecular size, the bubble-pressure line is found to be a linear function of composition as shown in Figs. 10.2 and 10.3. As was noted in Section 10.1, the T-x-y and P-x-y diagram shapes are related qualitatively by inverting one of the diagrams. Because the bubble pressure is a linear function of composition, we may write for a binary system,
Figure 10.2. (a), (b). Phase behavior of the methanol-ethanol system. Left figure at 50°C. Right figure at 760 mm Hg. (P-x-y from Schmidt, G.C. 1926. Z. Phys. Chem. 121:221, T-x-y from Wilson, A., Simons, E.L. 1952. Ind. Eng. Chem. 44:2214).
Figure 10.3. (a), (b) Phase behavior of the pentane-hexane system. Left figure at 25°C. Right figure at 750 mm Hg. (P-x-y from Chen, S.S., Zwolinski, B.J. 1974. J. Chem. Soc. Faraday Trans. 70: 1133, T-x-y from Tenn, F.G., Missen, R.W. 1963. Can. J. Chem. Eng. 41:12).
Figure 10.3. (c); (d) Phase behavior of the benzene-toluene system. Left figure at 79.7°C. Right figure at 760 mm Hg. (P-x-y from Rosanoff, M.A., et al. 1914. J. Am. Chem. Soc. 36:1993, T-x-y from Delzenne, A.O. 1958. Ind. Eng. Chem., Chem. Eng. Data Series. 3:224).
Dividing by P, we find the form of the bubble objective function summarized in Table 10.1,
Therefore, we conclude that the K-ratio for Raoult’s law4 is
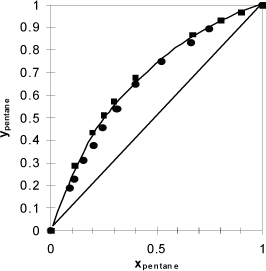
Throughout Chapters 10–16 and 18–19 we continually improve and refer to K-value models. The motivation for this focus on K-values is that they are used for all types of separations. For this select class of mixtures, the K-ratios depend only on T and P and are independent of composition. To calculate a K-ratio, we can use any method for the vapor pressure. Though we have derived the K-ratio empirically, we use this model to practice performing VLE calculations and return in future sections to a more fundamental derivation to explore more fully the restrictions for this model. In future chapters, we explore more sophisticated methods for estimating the K-ratio when Raoult’s law does not apply and the K-ratios depend on composition. In addition to the P-x-y and T-x-y plots, another common presentation of data for distillation studies is the x-y plot of coexisting compositions as shown in Fig. 10.4.
Figure 10.4. Data from Fig. 10.3 plotted with coexisting liquid and vapor values for each experimental tie line, resulting in the x-y plot. Note that the data do not superimpose exactly because one data set is isobaric and the other set is isothermal. Squares are T-x-y data. Circles are P-x-y data. The diagonal is traditionally drawn in an x-y figure, and the data never cross the diagonal for systems that follow Raoult’s law.
![]() K-values are used for all types of separations.
K-values are used for all types of separations.
François-Marie Raoult (1830–1901) was a French chemist who studied freezing point depression and the effect of mixing on bubble pressure. His first work on solution behavior in 1878 dealt with freezing point depression. His paper on “Raoult’s Law” was published in 1892.
Shortcut Estimation of VLE K-ratios
Given Raoult’s law and recalling the Chapter 9 shortcut procedure for estimating vapor pressures, it is very useful to consider combining these to give a simple and quick method for estimating ideal solution K-ratios. Substituting, we obtain the shortcut K-ratio,
Since the ideal solution model is somewhat crude anyway, it is not unreasonable to apply the above equation as a first approximation for any ideal solution when rapid approximations are needed.5
![]() Shortcut K-ratio for Raoult’s law. Not only is this expression restricted to Raoult’s law, but it is also subject to the restrictions of Eqn. 9.11.
Shortcut K-ratio for Raoult’s law. Not only is this expression restricted to Raoult’s law, but it is also subject to the restrictions of Eqn. 9.11.
Bubble Pressure
For a bubble-pressure calculation, writing ![]() as
as ![]() , which is
, which is  . Multiplying by P, we may write
. Multiplying by P, we may write
where no iterations are required because temperature, and therefore vapor pressures, are known. Once the bubble pressure is found, the value can be reinserted into Eqn. 10.6 to find the vapor mole fractions:
Dew Pressure
For a dew-pressure calculation, writing ![]() as
as ![]() and rearranging:
and rearranging:
which may be rearranged and solved without iteration, because the vapor pressures are fixed at the specified temperature:
Once the dew pressure is calculated, the value can be reinserted into Eqn. 10.6 to find the liquid mole fractions:
Bubble Temperature
For a bubble-temperature calculation, writing ![]() as
as ![]() , and rearranging:
, and rearranging:
To solve this equation, it is necessary to iterate on temperature (which changes Pisat) until P equals the specified pressure. Then the vapor phase mole fractions are calculated using Eqn. 10.9.
Dew Temperature
For a dew-temperature calculation, writing ![]() as
as ![]() , and rearranging:
, and rearranging:
To solve this equation, it is necessary to iterate on temperature (which changes Pisat) until P equals the specified pressure. Then the liquid phase mole fractions are calculated using Eqn. 10.12.
General Flash
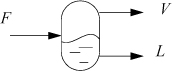
Flash drums are frequently used in chemical processes. For an isothermal drum, the temperature and pressure of the drum are known. Consider that a feed stream is liquid which becomes partially vaporized after entering the drum as illustrated in Fig. 10.5. The name of the flash procedure implies that it is applicable only for flashing liquids, but in fact, the procedure is also valid for vapor entering a partial condenser or for any number of incoming vapor and/or liquid streams with overall compositions specified by {zi} with overall flow rate F. To apply the procedure, the overall composition of the components, zi, total feed flow rate, F, and outlet T and P just need to be known before the procedure is started. Though the method is introduced using flowing streams, flow is not required for a flash calculation; the calculation can be performed for any overall composition constrained at a particular temperature and pressure even within a closed system. Also, the inlet stream temperature does not need to match the outlet temperature; the two outlet streams are at the specified temperature.
Figure 10.5. Illustration of a flash drum and variable definitions for streams. Note that F need not be a liquid; F may be all vapor or partial vapor. The principles can be applied to a nonflowing system as described for a binary on page 371.
The flash equations are easily derived by modification of the overall and component balances used in the development of the lever rule in Section 10.1. If z is the feed composition and V/F is the liquid-to-feed ratio, then L/F = 1 – V/F, and the component balance is zi = xi(L/F) + yi(V/F). Substituting for L/F from the overall balance, and using yi = xiKi, the component balance becomes zi = xi[(1 – V/F) + Ki(V/F)], which can be solved for xi:
using yi = xiKi, we may multiply Eqn. 10.15 by Ki to obtain yi.
One obvious thing to do at this point is to iterate to find the V/F ratio which satisfies ![]() . But the flash problem is different from the dew- and bubble-point problems because we must also solve
. But the flash problem is different from the dew- and bubble-point problems because we must also solve ![]() . Fortunately, a reliable successive substitution method has been developed by Rachford and Rice6 to solve this problem using the objective function
. Fortunately, a reliable successive substitution method has been developed by Rachford and Rice6 to solve this problem using the objective function ![]() . Introducing the variable Di ≡ xi – yi to denote the difference between xi and yi for each component,
. Introducing the variable Di ≡ xi – yi to denote the difference between xi and yi for each component, ![]() , we iterate on V/F until the sum approaches zero. For a binary system, using the Ki ratios, the objective function becomes
, we iterate on V/F until the sum approaches zero. For a binary system, using the Ki ratios, the objective function becomes
For Raoult’s law, Ki is a function of temperature and pressure only, both of which are fixed for an general flash calculation. The outlets are assumed to exit at phase equilibrium, and the exit conditions are used to calculate Ki. Therefore, in Eqn. 10.17, the only unknown is V/F. Eqn. 10.17 is monotonic in V/F; the sum always increases as V/F increases. Therefore, we search for the value of V/F which satisfies the equation. Note that 0 < V/F < 1 for a physically realistic answer. Outside this range, the system is either below the dew pressure (mathematically V/F > 1) or above the bubble pressure (mathematically V/F < 0). After finding V/F from our basis, then, L/F = 1 – V/F and stream compositions can be found from Eqns. 10.15 and 10.16.
Before executing a flash calculation by hand, bubble and dew calculations at the overall composition are recommended to ensures that the flash drum is between the bubble and dew pressures at the given temperature. (These calculations are easier than the flash calculation and may save you from doing it if the system is outside the phase envelope.) When using a computer, the value of V/F can be used to ascertain if the system is outside the two-phase region. If a computer flash calculation does not converge, then the bubble or dew should be performed to troubleshoot.
For a binary system, a flash calculation may be avoided by plotting the overall composition on the P-x-y diagram between the dew and bubble pressures and reading the vapor and liquid compositions from the graph. Application of the lever rule permits calculation of the total fraction that is vapor; however, this method requires a lot of calculations to generate the diagram if it is not already available and is limited to binary mixtures. Also, plotting the curves is slower than a direct calculation.
The steady-state energy balance for an general flash is given by
where we indicate a common method of calculation of the enthalpy of a mixture as the sum of the component enthalpies and the heat of mixing (Eqn. 3.24 on page 105). Writing in terms of V/F:
A reference state must be specified for each component, and a method for calculation of the enthalpy must be selected. A simple method of calculating enthalpies of vapors and liquids relative to reference states has been illustrated in Example 3.3 on page 107. For an isothermal flash, the VLE constraint, Eqn. 10.17, can be solved independently of the energy balance, and the energy balance can then be solved for the required heat transfer.
Adiabatic Flash
An adiabatic flash differs from an isothermal flash because ![]() in Eqn. 10.19. The adiabatic conditions will result in a temperature change from the feed conditions that is often significant. A typical scenario involves an outlet pressure less than the inlet pressure, resulting in an evaporation of a fraction of the feed. Because evaporation is endothermic, this type of flash results in a temperature drop (often significant). We have seen this type of calculation for pure fluids using throttles in Chapter 5. The additional complication with a mixture is that the components will distribute based on their different volatilities. The objective of an adiabatic flash calculation is to determine the outlet temperature in addition to the L and V compositions. An adiabatic flash requires that Eqn. 10.19,
in Eqn. 10.19. The adiabatic conditions will result in a temperature change from the feed conditions that is often significant. A typical scenario involves an outlet pressure less than the inlet pressure, resulting in an evaporation of a fraction of the feed. Because evaporation is endothermic, this type of flash results in a temperature drop (often significant). We have seen this type of calculation for pure fluids using throttles in Chapter 5. The additional complication with a mixture is that the components will distribute based on their different volatilities. The objective of an adiabatic flash calculation is to determine the outlet temperature in addition to the L and V compositions. An adiabatic flash requires that Eqn. 10.19, ![]() , must be solved simultaneously with Eqn. 10.17. The vapor and liquid mole fractions for Eqn. 10.19 are determined from Eqns. 10.15 and 10.16. The method is complex enough that even simple assumptions, such as ideal mixing (ΔHmix = 0), benefit from a computer algorithm.
, must be solved simultaneously with Eqn. 10.17. The vapor and liquid mole fractions for Eqn. 10.19 are determined from Eqns. 10.15 and 10.16. The method is complex enough that even simple assumptions, such as ideal mixing (ΔHmix = 0), benefit from a computer algorithm.
The algorithm to solve for the adiabatic flash depends on the differences in boiling points of the components. Usually the boiling points are different enough that an initial guess of T is used in VLE Eqn. 10.17 (where V and L are assumed to exit at the same T) to find an initial V/F where 0 < V/F < 1. With that initial V/F, then the V and L compositions (Eqns. 10.15 and 10.16) and then the energy balance (Eqn. 10.19) are evaluated, often scaling Eqn. 10.19 by dividing by 1000 when the enthalpy values are large. If the energy balance is not satisfied, then a new T trial is inserted into Eqn. 10.17 and the loop continues. Eqn. 10.19 is monotonic in T and increases when T decreases. When the boiling points are very close for all components, such as with isomers, the calculation converges better with an initial guess of V/F in Eqn. 10.17, which is solved by trial and error for the T which satisfies the equation. The L and V compositions and T are then used for the outlet enthalpies in Eqn. 10.19 to generate a new value for V/F and the iteration continues until convergence.
10.4. Multicomponent VLE Raoult’s Law Calculations
Extending our equations to multicomponent systems is straightforward. For a bubble calculation we have
For a dew calculation we have
These equations may be used for bubble- or dew-pressure calculations without iterations. For bubble- or dew-point temperatures, iteration is required. A first guess may be obtained from one of the following formulas:
But these are somewhat inaccurate guesses which require subsequent iteration.7
For flash calculations, the general formula is:
to find L/F and xi and yi are then found using Eqns. 10.15 and 10.16.
Use the next example to understand how to apply the strategies described in Section 10.2. Note how the column conditions are used to decide which routine to use. Note also that developing skill to determine which routine to run is as important as proficiency with the routines.
Example 10.1. Bubble and dew temperatures and isothermal flash of ideal solutions
The overhead from a distillation column is to have the following composition:
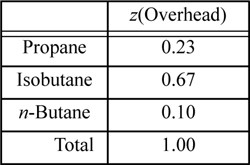
A schematic of the top of a distillation column is shown below. The overhead stream in relation to the column and condenser is shown where Vprod represents vapor flow and Dprod represents liquid flow. In an ideal column, the vapor leaving each tray (going up) is in phase equilibrium with the liquid leaving the same tray (going down). If the cooling water to the condenser is turned off, then only vapor product will be obtained, but this is not typical because the column works better with some liquid L returning to the column. To obtain liquid product only, cooling water is provided and the vapor product stream is turned off, and the condenser is known as a total condenser. If cooling water is provided to partially condense the vapor stream, the liquid product stream is typically turned off. Then the condenser provides additional separation, operating as a partial condenser. In an ideal partial condenser, the exiting vapor and liquid leave in phase equilibrium with each other.

a. Using the shortcut K-ratio, calculate the temperature at which the condenser must operate in order to condense the overhead product completely at 8 bar.
b. Using the shortcut K-ratio, and assuming the overhead product vapors are in equilibrium with the liquid on the top plate of the column, calculate the temperature of the overhead vapors and the composition of the liquid on the top plate when operating at the pressure of part a.
c. The vapors are condensed by a partial condenser operating at 8 bar and 320 K. Using the shortcut K-ratio, what fraction of liquid is condensed?
Use the shortcut estimates of the K-ratios. Use of a solver tool is recommended after developing an understanding of the manual iterations summarized below.
a. To totally condense the overhead product, the mixture must be at the bubble-point temperature or lower. The maximum temperature is the bubble-point temperature. To find the bubble-point temperature for the ternary system, we apply Eqn. 10.20 extended to three components. The calculation requires trial-and-error iteration on temperature as summarized in Table 10.1.
Tabulated below, the shortcut K-ratio is calculated using Eqn. 10.7 at each temperature guess at 8 bar, and the y values from Eqn. 10.9 are summed to check for convergence following the procedure set forth in Table 10.1. Iterations are repeated until the y’s sum to 1.
![]() It is easy to create an Excel spreadsheet to do these calculations quickly (e.g., Flshr.xlsx can be modified).
It is easy to create an Excel spreadsheet to do these calculations quickly (e.g., Flshr.xlsx can be modified).

The temperature has been bracketed, interpolating,
The temperature has been bracketed, interpolating,
b. The saturated vapor leaving the tray is in equilibrium with the liquid and is at its dew-point temperature at 8 bar. Eqn. 10.21 is used. The calculation requires iteration on temperature. Calculating the Ki ratios as in part (a), the liquid phase compositions are calculated at each iteration using Eqn. 10.12 until the values sum to 1.

Repeating the procedure at this temperature a final time results in the liquid compositions,

c. Recognize that the solution involves an isothermal flash calculation because P and T are both specified. Begin by noting that the specified condenser temperature is between the bubble temperature, 317 K, and the dew temperature, 324 K, so vapor-liquid equilibrium is indeed possible. Because T and P are already set, Eqn. 10.7 is used to calculate the K-ratio for each component. Then, we seek a solution for Eqn 10.23 at 320 K and 8 bar. In the general flash routine, Fflash, Vflash, and Lflash are used to denote the flow rates for the flash drum and we must adapt the flash variables to the column stream names. We add “flash” and “column” subscript descriptors for increased clarity. In the solution, Fflash, Vflash, and Lflash represent the flow rates for the partial condenser, Fflash = V1,column, Vflash = Vprod, and Lflash = Dprod + Lcolumn. In the summarized calculations below, Vflash/Fflash = Vprod/V1,column and Di in the table is the objective variable for the flash calculation as used in Eqn. 10.23, not the column liquid product flow rate Dprod. Each table column summarizes a guess for flash ratio Vflash/Fflash and the resultant flash objective variable Di. The composition of the feed is given by zi as conventional for a flash calculation, which is the composition of V1,column.
A summary of the isothermal flash calculation is given below.:
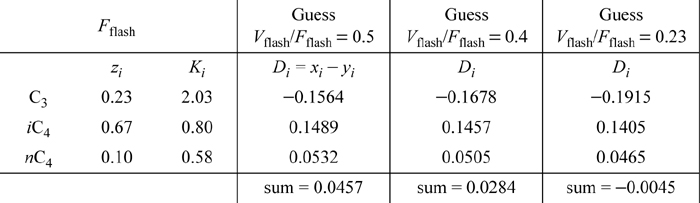
Interpolating between the last two results that bracket the answer,
Vflash/Fflash = 0.25, applying Eqns. 10.15 and 10.16,
⇒ {xi} = {0.1829, 0.7053, 0.1117} and {yi} = {0.3713, 0.5642, 0.0648}
The compositions can be confirmed to be converged. The outlet composition of the vapor, Vprod, is given by {yi} and it is clearly more enriched in the volatile components than the inlet from the top of the column V1,column.
Note: The flash problem converges more slowly than the bubble- and dew-point calculations, so the third iteration is necessary.
Ethanol + methanol form a nearly ideal solution as shown in Fig. 10.2. An equimolar feed at 760 mmHg is subjected to an adiabatic flash operating at 200 mmHg. Feed enters at 70°C and 43 mol/min. Find the exiting stream temperatures, flow rates, and compositions. Assume ideal solutions and use the Antoine equation for vapor pressures.
Solution
This is a direct application of a procedure, so it is clear which VLE routine to use: the FA row of Table 10.1. We must combine the VLE procedure with energy balance. A bubble-pressure calculation at 70°C (not shown) shows that the feed is all liquid. Two solutions are provided using different pathways for the enthalpy calculations. Both solutions will use the same flash calculation procedures and the Antoine equation is used with {methanol, ethanol}:
A = {8.081, 8.1122}, B = {1582.3, 1592.9}, C = {239.73, 226.18}
Solution 1
This solution method calculates component enthalpies using a reference state of liquid at 25°C for all species where we set HR = 0. The enthalpy calculations use the pathway of Fig. 2.6(a). The pathway is taken through the boiling point of each component, as in Example 3.3. To compute stream enthalpies, we use ideal solutions as shown in Example 3.3, ignoring heat of mixing. Heat capacity constants and heats of vaporization are taken from Appendix E.
The solution requires a guess of T resulting in 0 ≤ V/F ≤ 1 that provides two phases, and then a check of the energy balance. Due to the complexity of the calculation, we iterate on the T guess manually, and automate the tedious parts of solving for V/F and checking the energy balance. The solution is provided in MATLAB file Ex10_02.m. Some intermediate results are tabulated.
Because a computer is used, we skip preliminary bubble and dew calculations. Note that we do not tabulate all values until 0 ≤ V/F ≤ 1. The first guess of 45°C is above the dew temperature. The second guess of 35°C is below the bubble temperature. The next guess happens to give a condition close to the bubble temperature, so we raise the temperature guess slightly. The column OBJEB = (Eqn. 10.19)/1000. The compositions and enthalpies are shown below and the last row is converged. The exiting flow rates are V = V/F(43) = 0.09(43) = 3.87 mol/min, and L = 43 – 3.87 = 39.13 mol/min. About 9% (molar basis) of the inlet is flashed, and the outlet temperature is 40.2°C compared to an inlet of 70°C.

Solution 2
This solution method calculates component enthalpies using the pathway of Fig. 2.6(c), the reference state of the elements at 25°C, the heats of formation of ideal gases, the generalized correlation for heat of vaporization in Eqn. 2.45, and the Cpig(25°C) from the back flap. The results are slightly different from Solution 1, owing to the imprecision of Eqn. 2.45 and differences between the heat capacities. Process simulation software typically uses this enthalpy path and reference state.
We begin by finding the enthalpy of the feed relative to the elements at 25°C, noting that it is a liquid ideal solution. HF = HL(70°C) = Σ xi(ΔH°Cf,i + Cpig(T–TR) – ΔHivap) = 0.5(–200,940 + 5.28(8.314)(70 – 25) – 35,976) + 0.5(–234,950 + 7.88(8.314)(70 – 25) – 38,595) = –252,769 J/mol. This takes care of the first term in Eqn. 10.19. Noting that the feed is liquid, we might suspect the flash outlet to be mostly liquid. Performing a bubble-temperature calculation at 200 mmHg gives T = 40.00°C and HL(40°C) = –256,901 and with no vapor stream results in Q = –4132 J/mol.a The temperature must be slightly higher to move Q toward zero. Suppose we “guessed” that the temperature is 40.23°C.b Then the flash calculation gives xEtOH = 0.5173, yEtOH = 0.3515, V/F = 0.1042, HL(40.23°C) = –257,502. The formula for HV is similar to that for HL but omits the ΔHivap contribution and replaces xi with yi, so HV(40.23°C) = –212,088. Following Eqn. 10.19, Q = (1 – 0.1042)(–257,502) + 0.1042(–212,088) + 252,769 = 0.1 J/mol. We may assume that 0.1 J/mol is sufficiently close to zero.
a. Note that the heats of vaporization must be recomputed at the new temperature.
b. Obviously, this was not our first guess. Alternatively, you could call the solver with the added constraint that Q = 0 while Σ Di = 0 by changing T and V/F simultaneously.
10.5. Emissions and Safety
Hydrocarbon emission monitoring is an important aspect of environmentally conscious chemical manufacturing and processing. The United States Environmental Protection Agency (EPA) has published guidelines8,9,10 on the calculations of emissions of volatile organic compounds (VOCs), and VOC emissions are monitored in the U.S. Most of the emission models apply the ideal gas law and Raoult’s law and thus the calculation methods are easily applied. While many of the mixtures represented with these techniques are not accurately modeled for phase equilibria by Raoult’s law, the method is suitable as a first approximation for emission calculations. This section explores emission calculations for batch processes. Batch processes are common in specialty chemical manufacture. In most cases, air or an inert gas such as nitrogen is present in the vapor space (also known as the head space). In some cases, the inert head space gas flows through the vessel, and is called a purge or sweep gas. These gases typically have negligible solubilities in the liquid phase and are thus considered noncondensable. There are several common types of unit operations encountered with VOC emissions, which will be covered individually.
Filling or Charging
During filling of a tank with a volatile component, gas is displaced from the head space. The displaced gas is assumed to be saturated with the volatile components as predicted with Raoult’s law and the ideal gas law. Initially in the head space, ![]() and after filling,
and after filling, ![]() , where the subscript head indicates the head space. The volume of liquid charged is equal to the volume change of the head space. The mole fractions of the VOC components are determined by Raoult’s law, and the noncondensable gas makes up the balance of the head space. The moles of VOC emission from the tank are estimated by
, where the subscript head indicates the head space. The volume of liquid charged is equal to the volume change of the head space. The mole fractions of the VOC components are determined by Raoult’s law, and the noncondensable gas makes up the balance of the head space. The moles of VOC emission from the tank are estimated by ![]() for each VOC.
for each VOC.
Purge Gas (Liquid VOC Present)
When a purge (sweep) gas flows through a vessel containing a liquid VOC, the effluent will contain VOC emissions. At the upper limit, the vessel effluent is assumed to be saturated with VOC as predicted by Raoult’s law. For VOC component i,
where ![]() , where the sum is over VOCs only. The variable km is the saturation level, and is set to 1 for the assumption of saturation and adjusted lower if justified when the purge gas is known to be unsaturated. The flow of noncondensables nsweep can be related to a volumetric flow of purge gas using the ideal gas law,
, where the sum is over VOCs only. The variable km is the saturation level, and is set to 1 for the assumption of saturation and adjusted lower if justified when the purge gas is known to be unsaturated. The flow of noncondensables nsweep can be related to a volumetric flow of purge gas using the ideal gas law,
Purge Gas (No Liquid VOC Present)
Vessels need to be purged for changeover of reactants or before performing maintenance. After draining all liquid, VOC vapors remain in the vessel at the saturation level present before draining. The typical assumption upon purging is that the vessel is well mixed. A mole balance on the VOC gives ![]() ; dividing by yi the equation becomes
; dividing by yi the equation becomes ![]() . The left-hand side can subsequently be written ntankdyi/yidt = (PVtank)/(RTtank) · (dyi)/(yidt), and the right-hand side can be written
. The left-hand side can subsequently be written ntankdyi/yidt = (PVtank)/(RTtank) · (dyi)/(yidt), and the right-hand side can be written ![]() . When the sweep gas and tank are at the same temperature, which is usually a valid case, the equation rearranges to
. When the sweep gas and tank are at the same temperature, which is usually a valid case, the equation rearranges to ![]() , which integrates to
, which integrates to
The emissions are calculated by
Heating
During a heating process, emissions arise because the vapors in the head space must expand as the temperature rises. Since vapor pressure increases rapidly with increasing temperature, VOC concentrations in the vapor phase increase also. Detailed calculations of emissions during heating are somewhat tedious, so an approximation is made; the emission of each VOC is based on the arithmetic average of the molar ratio of VOC to noncondensable gas at the beginning and the end of the heating multiplied by the total moles of noncondensable gas leaving the vessel. At the beginning of the heating, representing the VOC with subscript i and the noncondensables with subscript nc, the ratio of interest is (ni/nnc)i = (yi/ync)i = (yiP/yncP)i, and at the end (ni/nnc)f = (yi/ync)f = (yiP/yncP)f. The emission of VOC component i is calculated as
where ![]() , and the sum is over VOCs only. The value of Δnnc is given by
, and the sum is over VOCs only. The value of Δnnc is given by
where the summations are over VOCs only and Δnsweep is the total moles of noncondensable that are swept (purged) through the vessel during heating and is set to zero when purging is not used. Eqns. 10.29 and 10.30 can overestimate the emissions substantially if the tank approaches the bubble point of the liquid because ync approaches zero, and then calculations are more accurately handled by a more tedious integration. The integration can be approximated by using the method presented here over small temperature steps and summing the results.
Depressurization
Three assumptions are made to model depressurizations: The pressure is decreased linearly over time; air leakage into the vessel is negligible; and the process is isothermal. The relationship is then the same as Eqn. 10.29, where Δnnc is calculated by Eqn. 10.30 using Δnsweep = 0.
Other Operations
Other operations involve condensers, reactors, vacuum vessels, solids drying, and tank farms. Condensers are commonly used for VOC recovery; however, the VOCs have a finite vapor pressure even at condenser temperatures and the emissions can be calculated by using Eqns. 10.25 and 10.26 at the condenser temperature. Reactors may convert or produce VOCs and, in a vented reactor, the emissions can be calculated by adapting one of the above techniques, keeping aware that generation of gas causes additional vapor displacement and possible temperature rise due to reaction. Vacuum units and solids-drying operations are also direct adaptations of the methods above. Tank farm calculations are more detailed and empirical. Tank emission calculations depend on factors such as the climate and the paint color of the tank. Fixed roof tanks must breathe as they warm during the day due to sunlight, and then cool during the night hours. There are also working losses due to routine filling of the tanks as covered above. Although heating and cooling in a tank with a static level can be treated by the methods presented above, when the levels are also changing due to usage, EPA publications are recommended for these more tedious calculation procedures.
Flash Point
The flash point is a property much different from that represented by the general flash or adiabatic flash discussed earlier. Fire requires fuel, an oxidizer (air in this case), and an ignition source. The flash point is the temperature above which a vapor mixture supports combustion when an ignition source is present. When liquids burn, fire occurs on a liquid surface; the vapors near the surface are burning, not the liquid itself. The flash point is important because it is the temperature at which the Lower Flammability Limit (LFL) concentration is reached at the liquid surface. A flash can also occur entirely in the vapor phase. When burning buildings explode in action movies, the movies are depicting the real condition of the vapors in the building reaching the flash point as plastics and other materials decompose. Fire fighters are very cautious entering buildings where a potential for such explosions exist.
![]() The Chemical Safety Board is a federal agency charged with investigating chemical accidents. The goal is to learn from accidents and improve safety.
The Chemical Safety Board is a federal agency charged with investigating chemical accidents. The goal is to learn from accidents and improve safety.
The Chemical Safety Board (www.csb.gov) tracks accidents in the U.S. chemical industry. The CSB reports that workers continue to be careless with ignition sources near organic solvents. Earlier sections discussed the warming of a tank during the day. As a vented tank warms, emissions may reach the LFL as the day warms. Maintenance on metal tanks often involves grinding or welding, which introduces ignition sources and has resulted in numerous deaths and disfigurements as well as property damage. Raoult’s law may be used to estimate the vapor phase concentrations, and the flash point temperature is approximately the temperature where y·(100%) = LFL. Technically, the LFL defined as a volume percent of combustible material, but it is the same as the mole fraction in an ideal gas. For a mixture, the flash point can be calculated approximately by the empirical relation
Because combustion requires an oxidizer, each fuel also has an Upper Flammability Limit (UFL) above which there is not enough oxygen present to maintain combustion. Most accidents occur near the LFL, which is the motivation for more discussion of LFL. Both the LFL and the UFL are affected by inerts because of the effect on the ratio of oxidizer to fuel.
10.6. Relating VLE to Distillation
We introduced some major points about the importance of distillation in Section 3.2. Roughly 80% of separations are done involving distillation and 70% of the capital cost of a chemical plant goes into distillation equipment, and thus the proper application of vapor-liquid equilibria and design are essential. Usually, one distillation column is required to separate any two components. To separate three components to high purity requires two columns. Obtaining four components to high purity requires three columns, and so forth. So a single reactor that requires two reactants and produces two products (A + B → C + D) would probably require three distillation columns downstream if all the components are desired in high purity. Pharmaceutical and speciality chemical plants have more by-products than bulk chemical plants. This means that chemical engineers need to be fairly familiar with VLE, especially in the fine chemicals industry.
How Distillation Works
How does the laboratory experiment (Fig. 10.6(a)) relate to distillation in a chemical plant (Fig. 10.6(b) and (c))? We begin with an elementary introduction to the conceptual basis of distillation. We then follow up with more detailed descriptions of the basis for modeling the process.
Figure 10.6. Schematic diagrams of distillation columns. (a) A typical chemistry laboratory distillation apparatus; (b) close-up view of sieve trays showing the holes in the trays, downcomers, and liquid on each tray; (c) a partial condenser operates like a flash unit.
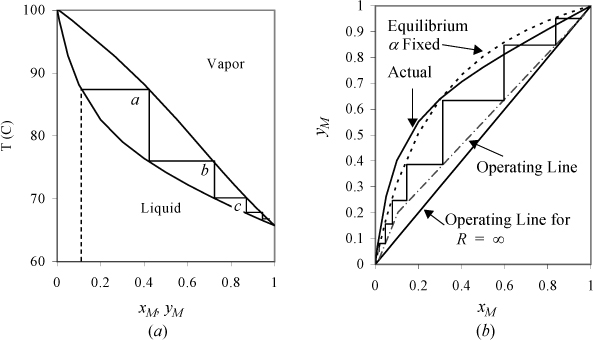
Thermodynamics teaches us that the most volatile components are enriched in the vapor phase when a liquid solution is boiled. For example, suppose that you want to recover methanol (a potential transportation fuel or reactant for a fuel cell) from a mixture of 10% methanol (MeOH) and 90% water. The thermodynamics of the methanol + water system are summarized in Fig. 10.7. Fig. 10.7(a) shows that the solution bubble-point temperature is ~87°C. As it boils, the temperature remains constant, but the vapor composition leaving the vessel is ~40 mol% MeOH. Let us call this separation stage a. Forty percent is a big improvement over the initial 10%, but it is still mostly water. What can you do to make it more pure? Why not condense the vapor to a liquid and collect it in a separate pot to reboil it? After you have enough solution in that pot, take it to another boiler and perform stage b, then repeat for stages c, d, e as shown in Fig. 10.7(a). After ~5 stages, you could obtain 98% pure methanol. This is a simplification of multistage distillation at the conceptual level. (Note that most process simulation software numbers stages from the column top which is why we designated stages as letters rather than numbering from the bottom.) As outlined so far, it is inefficient and oversimplified because we considered the liquid phase composition to be invariant while the volatile component was boiling off. Separation textbooks provide the details on the mass balances.
Figure 10.7. Stage-wise separation of methanol (M) and water. (a) T-x,y diagram at 1 bar, showing stages. (b) McCabe-Thiele analysis based on assuming constant relative volatility, αLH = [(αLHT)(αLHB)]½ (dotted line) compared with experimental curve.
The first law of thermodynamics tells us that energy is conserved. What if we could use the heat of condensing the vapor from stage a as the heat of boiling in stage b? That would be a big improvement. Furthermore, we can achieve this in minimal space if we use some clever plumbing. If we put the pot for stage b on top of stage a, and put little holes in the bottom of the pot, then the vapor boils through the holes faster than the liquid can weep back (Fig. 10.6(b)). The boiling point of the mixture on stage b is lower than the vapor temperature coming from below (cf. Fig. 10.7(a)). When the warmer vapor from stage a contacts the cooler liquid on stage b, it condenses. But the first law tells us that the heat of condensation must go somewhere. Where? It goes into boiling the liquid on stage b. Then we can do the same thing for stages c, d, e. This approach is called a tray distillation column and it is very common throughout the chemical industry. Roughly 70% of distillation columns are tray type.
We still have not addressed how tray distillation relates to the chemistry lab. The chemistry lab requires some gauze or glass wool in the glass tube above the boiling flask. Because of heat loss through the condenser walls, some of the boiling liquid condenses, then trickles down the gauze and falls back into the boiling flask. This trickling liquid serves the same function as the liquid on the trays, but of course the contact and mass exchange is much less efficient. On the other hand, we can generate a lot of surface area and a lot of vapor-liquid contact by using a lot of gauze. In the chemical industry, columns based on this principle are called packed columns. Packed columns comprise the other 30% of distillation columns. There is another big difference between the chemical industry and chemistry lab. The vast majority of industrial columns run in continuous steady-state mode, not batch mode like the chemistry lab. This means that continuous feed enters on a stage that has a similar composition to the feed.
Most mixtures contain more than two components. It is common, however, to design the multicomponent column based on the separation of two key components. Because boiling point (in the absence of azeotropes discussed later) increases with Mw, it is common to discuss separation based on light components (more volatile) moving up the column, and heavy components moving down. For preliminary column design a volatile light key (typically low Mw, thus light) and less volatile heavy key component are designated. Splitting two key components implicitly splits components lighter than the “light key” component from components heavier than the “heavy key” component. The split (S) is the fraction that exits with distillate. The light key (LK) component is the least volatile component with a split SLK > 0.5. System components lighter than the light key must be even more volatile and exit as distillate. For example, consider a distillation of hexane, octane, decane, and dodecane. If we designate octane as the light key, then the of hexane should also go out the top. The heavy key is the lightest component (most volatile) with a split SHK < 0.5. In the example, we could select decane as the heavy key and thus dodecane would go out the bottom also. In a perfect world, the splits would be 100% for the light key and 0% for the heavy key, but that would require an infinitely tall distillation column. More typical splits are 99% and 1%.
The split fractions define the relevant mass balances in distillation. The thermodynamics relevant to distillation is implemented using the relative volatility in terms of the VLE K-ratios,
For the case of light and heavy key components,
For Raoult’s law, the K-ratios are independent of composition, and thus is the relative volatility,
For systems that don’t follow Raoult’s law, the relative volatility may vary through the column owing to composition changes, but distillation is feasible as long as αLH > 1. (We will show the analysis for the nonideal αij calculation in Section 11.11 on page 442.) The presence of other components is of secondary concern for preliminary column design as long as αLH > 1, so shortcut column analysis treats LK and HK as if the mixture were binary. It may be possible to improve αLH through the addition of other components (e.g., extractive distillation), but that merely reinforces the requirement of the overall system to the mandate that αLH > 1.
For the sake of modeling, the tray column is simplest to introduce as illustrated in Fig. 10.7(b). Fig. 10.7(b) focuses on the composition changes only, neglecting the temperature effects. Fig. 10.7(b) also shows the result of approximating that the relative volatility is constant. A larger αij results in a larger area under the x-y curve and an easier separation. If αij = 1, the curve collapses on the 45° diagonal. The diagram shows “steps” between the equilibrium line and the operating line. The equilibrium line represents the compositions at each tray as they leave. The operating line represents the compositions between trays. Moving up and down the column, the material balances are shown graphically by stepping back and forth as we relate the material balance “on stage” and “in-between stage.” Comparing the curves for actual and constant αij, note that a similar number of stages is obtained. For the purposes of our model, constant relative volatility is a convenient approximation for the equilibrium curve as shown. But there is still a significant detail that has been omitted in our conceptual outline of distillation. Where did the liquid come from that is on the trays of the tray column?
Fig. 10.6(c) shows how the condenser on top of the column pours liquid back down to keep some on the trays. The part that we pour back down the column (L) is called reflux. The part that we recover as product is called distillate (D). The ratio of L/D is called the reflux ratio (R). The reflux ratio controls the amount of product recovered as distillate. If we actually want to recover some product (i.e., D ≠ 0), then we must accept some value R ≠ ∞. Finite values for R lead to the dashed-dot operating lines in Fig. 10.7(b). To understand this, consider that the 45° diagonal on Fig. 10.7(b) corresponds to L/V = 1. It turns out that taking distillate from the top of the column leads to slightly less separation on every stage, giving the dashed-dot lines of Fig. 10.7(b). Typical courses in mass transfer operations explain how to estimate the dashed-dot lines from values of R. The key point for now is that the value of R cannot be zero, or we will have no liquid on the trays, and it cannot be infinite or we will recover no product. We can go a little further and say that it must be closer to infinity for a distillation that has a relative volatility very near to unity, because the y-x curve in that case stays very close to the diagonal. Beyond that, we simply need to accept that somebody has analyzed this before and developed some equations for computing the minimum number of stages to achieve a desired separation (at infinite reflux), the minimum reflux ratio, and the actual number of stages. This is indeed the case, and the model equations are presented below.
A shortcut distillation calculation for the height of the column for constant relative volatility can be estimated from the Fenske equation,
where Nmin is the minimum number of theoretical trays at infinite reflux and ![]() is the geometric mean of the relative volatility calculated using the column top and bottom compositions, T and P. Typically, the number of actual trays is Nact ~ 4Nmin, with the space between trays being 0.6m. So a column with 99 and 1% splits and a relative volatility of 3 would have Nmin = 8.4 and a height of 20 m. With this background, the importance of the K-ratios and αLH becomes clear. Note that if αLH = 1, then Nmin = ∞. The relative volatility changes with composition for nonideal systems, and goes to 1 when an azeotrope exists. Then Eqn. 10.35 is not valid. We discuss such behavior in the following sections, and find significant motivation to understand the modeling of such systems in subsequent chapters.
is the geometric mean of the relative volatility calculated using the column top and bottom compositions, T and P. Typically, the number of actual trays is Nact ~ 4Nmin, with the space between trays being 0.6m. So a column with 99 and 1% splits and a relative volatility of 3 would have Nmin = 8.4 and a height of 20 m. With this background, the importance of the K-ratios and αLH becomes clear. Note that if αLH = 1, then Nmin = ∞. The relative volatility changes with composition for nonideal systems, and goes to 1 when an azeotrope exists. Then Eqn. 10.35 is not valid. We discuss such behavior in the following sections, and find significant motivation to understand the modeling of such systems in subsequent chapters.
10.7. Nonideal Systems
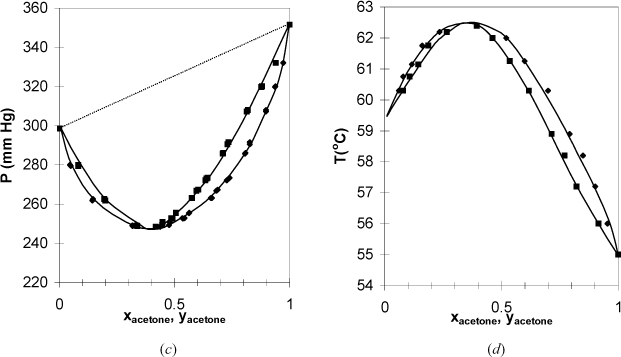
In Section 10.3 we introduced Raoult’s law for mixtures where the components have very similar chemical functionality and molecular weight. We have seen how easy the ideal-solution calculations can be. However, Raoult’s law is accurate for only a few of the systems you will encounter in practice. Examples of phase diagrams which deviate from Raoult’s law are shown in Fig. 10.8 and Fig. 10.9. There are several features of these diagrams that introduce important concepts. First of all, the Raoult’s law bubble lines are shown as dotted lines in the P-x-y diagrams to emphasize the deviations. Note again that the phase diagrams of each P-x-y/T-x-y pair can be qualitatively related by inverting one diagram of the pair.
Figure 10.8. (a), (b) Phase behavior of the methanol + 3-pentanone system. Left figure at 65°C. Right figure at 760 mm Hg. (T-x-y from Glukhareva, M.I., et al. 1976. Zh. Prikl. Khim. (Leningrad) 49:660, P-x-y calculated from fit of T-x-y.)
Figure 10.8. (c), (d) Phase behavior of the 2-propanol + water system. Left figure at 30°C. Right figure at 760 mm Hg. (T-x-y from Wilson, A., Simons, E.L., 1952. Ind. Eng. Chem. 44:2214, P-x-y from Udovenko, V.V., and Mazanko. T.F. 1967. Zh. Fiz. Khim. 41:1615.)
Figure 10.9. (a), (b) Phase behavior of the acetone + acetic acid system. Left figure at 55°C. Right figure at 760 mm Hg. (T-x-y from York, R., Holmes, R.C. 1942. Ind. Eng. Chem. 34:345, P-x-y from Waradzin, W., Surovy, J., 1975. Chem. Zvesti 29:783.)
Figure 10.9. (c); (d) Phase Behavior of the acetone + chloroform system. Left figure at 35.17°C. Right figure at 732 mm Hg. (T-x-y from Soday, F., Bennett, G.W., 1930. J. Chem. Educ. 7:1336, P-x-y from Zawidzki, V.J., 1900. Z. Phys. Chem. 35:129.)
![]() Positive deviations from Raoult’s law. It is convenient to say that the components “dislike” each other.
Positive deviations from Raoult’s law. It is convenient to say that the components “dislike” each other.
In Fig. 10.8 the bubble line lies above the Raoult’s law line, and these systems are said to have positive deviations from Raoult’s law. Positive deviations occur when the components in the mixture would prefer to be near molecules of their own type rather than near molecules of the other component. Briefly, it is convenient to say that these components “dislike” each other. The 2-propanol + water system has vapor pressures that are close to each other relative to the deviation from ideality. As a result, the positive deviations are large enough to cause the pressure to reach a maximum (i.e,. Pmax > P1sat > P2sat). The presence of a maximum (or minimum) causes the phase envelope to close at a composition known as the azeotropic composition. The nearness of the vapor pressures matters, because any deviation from ideality would give a maximum (or minimum), known as an azeotrope, if P1sat = P2sat. As a counterexample, the methanol + 3-pentanone system has significantly different vapor pressures for the components, and the deviations from ideality are not large enough to cause azeotrope formation. Recalling that the dew and bubble lines represent coexisting compositions at equilibrium, a maximum or minimum means that xi = yi and relative volatility αij = 1 at the azeotrope: αij > 1 on one side of the azeotrope composition and αij < 1 on the other side. This means that distillation ceases to provide separation at an azeotrope composition, and knowledge of azeotropes is critical for distillation design. When an azeotrope forms in a system with positive deviations, the azeotrope is a maximum on the P-x-y diagram and a minimum on the T-x-y diagram. To give a name to the type of azeotrope, the convention is to refer to azeotropes like that of 2-propanol + water as a minimum boiling azeotrope, referring to the boiling temperature reaching a minimum in composition. This can be confusing because the deviations from ideality are referred to as positive with respect to Raoult’s Law on a P-x-y diagram. If you remember that “boiling” refers to boiling temperature, it may help you to reduce confusion. The azeotrope on a P-x-y diagram is a maximum pressure azeotrope. Since the vapor and liquid compositions are equivalent at the azeotrope, a flash drum or distillation column cannot separate a mixture at the azeotropic composition.
![]() Relative volatility equals 1 for an azeotrope: αij > 1 on one side of the azeotrope composition and αij < 1 on the other side.
Relative volatility equals 1 for an azeotrope: αij > 1 on one side of the azeotrope composition and αij < 1 on the other side.
Azeotropes create challenges for chemical engineers. Azeotropic compositions for systems with either positive or negative deviations depend on temperature and pressure, however the dependencies are usually weak unless large pressure or temperature changes are made. For example, the ethanol + water system possesses an azeotrope that is widely known. This azeotrope causes a significant contribution to the high energy cost of bioethanol. Separating ethanol from the dilute fermentation product stream consumes about one-third of the energy content of the ethanol. Are there ways to separate ethanol more efficiently? Are there alternative fermentation products that can be produced without an azeotrope? Could fermentation (and copious amounts of water) be circumvented altogether and cellulose converted directly to chemical feedstocks similar to how heavy oils are cracked to ethylene? These are questions that a chemical engineering perspective brings to bear on these challenging problems. In the thermodynamics of phase equilibria, we are primarily concerned with distillation, liquid-liquid extraction, and azeotropes. Ideal solutions do not form azeotropes and they do not form immiscible liquid phases. Thus, Raoult’s law is incapable of representing these systems.
![]() Negative deviations from Raoult’s law. It is convenient to say that the components “like” each other.
Negative deviations from Raoult’s law. It is convenient to say that the components “like” each other.
In Fig. 10.9 the systems have negative deviations from Raoult’s law because the bubble line lies below the Raoult’s line. Similar azeotropic behavior is found in these systems if the vapor pressures are close to each other or the deviations are large. When an azeotrope forms in a system with negative deviations, the azeotrope is a minimum on the P-x-y diagram and a maximum on the T-x-y diagram. Therefore, this behavior is called a maximum boiling azeotrope or a minimum pressure azeotrope. From a chemical perspective, negative deviations indicate that the components “like” each other more than they like themselves. For example, mixing two acids may form an ideal solution, but mixing an acid with a base can give a negative deviation from ideality that feels warm to the touch. This is consistent with the negative sign on exothermic heats of reaction.
To better understand the reasons that mixtures deviate from Raoult’s law, we need to explore the fundamental thermodynamic principles and the assumptions underlying Raoult’s law. In doing so, we reveal the thermodynamic behavior that is necessary for Raoult’s law, and more greatly appreciate the reasons for the occasional success and more frequent failure of the model. Raoult’s law was developed empirically. To understand the true thermodynamic basis of Raoult’s law, it is necessary to “evaluate” how thermodynamic properties depend on composition. In addition, we can show that the fugacity used in Chapter 9 for pure fluids extends to mixtures and the component fugacity is the starting point for phase equilibria in mixtures. Raoult’s law involves specific assumptions about component fugacities for both the vapor and liquid phases. We develop models for deviations from Raoult’s law in Chapters 11–13.
10.8. Concepts for Generalized Phase Equilibria
Generalization of pure-component principles to multicomponent systems requires that we consider how the thermodynamic properties change with respect to changes in the amounts of individual components. For a pure fluid, the natural properties were simply a function of two state variables. In multicomponent mixtures, these energies and the entropy also depend on composition.
Note that these equations follow the mathematical rules developed in Chapter 6. Each term on the right-hand side consists of a partial derivative with respect to one variable, with all other variables held constant. The summation is simply a shorthand method to avoid writing a term for each component. The subscript nj ≠ i means that the moles of all components except i are held constant. In other words, for a ternary system, ((∂U)/(∂n1))P, T, nj ≠ i means the partial derivative of U with respect to n1 while holding P, T, n2, and n3 constant. For phase equilibria where P and T are manipulated, Eqn. 10.37 is more useful than Eqn. 10.36 because the Gibbs energy is a natural function of P and T. At constant moles and composition of material, the mixture must follow the same constraints as a pure fluid. That is, the state is dependent on only two state variables if we keep the composition constant.
⇒ (∂G/∂P)T,n = V and (∂G/∂T)P,n = – S;
These complicated-looking derivatives are really fundamental properties; therefore, we can rewrite Eqn. 10.37 as
The quantity (∂G/∂ni)P, T, nj ≠ i tells us how the total Gibbs energy of the mixture changes with an infinitesimal change in the number of moles of species i, when the number of moles of all other species fixed, and at constant P and T. The quantity (∂G/∂ni)P, T, nj ≠ i will become very important in our later discussion. so we give it a name, called the chemical potential, and give it a symbol.
We commonly write
Partial Molar Properties
Another name for the special derivative of Eqn. 10.39 is the partial molar Gibbs energy. We may generalize the form of the derivative and apply it to other properties. For any extensive thermodynamic property M, we may write ![]() . Note that T, P, and nj ≠ i are always held constant for a partial molar property. The overbar indicates a partial molar quantity, that is, for total volume V, the quantity (∂V/∂ni)T,P,nj≠i is called the partial molar volume and given the symbol
. Note that T, P, and nj ≠ i are always held constant for a partial molar property. The overbar indicates a partial molar quantity, that is, for total volume V, the quantity (∂V/∂ni)T,P,nj≠i is called the partial molar volume and given the symbol ![]() . Suppose we were considering a mixture of 500 red balls of size σR and 700 blue balls of size σB. How would the total volume change if we added one more red ball, keeping 700 blue balls? This is a finite difference example of the derivative called the partial molar volume of red balls. A special mathematical result of the differentiation is that we may write at constant temperature and pressure:
. Suppose we were considering a mixture of 500 red balls of size σR and 700 blue balls of size σB. How would the total volume change if we added one more red ball, keeping 700 blue balls? This is a finite difference example of the derivative called the partial molar volume of red balls. A special mathematical result of the differentiation is that we may write at constant temperature and pressure:
![]() Partial molar quantities provide a mathematical way to assign the overall mixture property according to composition expressed in moles or mole fractions.
Partial molar quantities provide a mathematical way to assign the overall mixture property according to composition expressed in moles or mole fractions.
As a result, we may write
We will return to these basic equations as we develop more relations for mixtures.
The chemical potential becomes an important term for each of the key properties, U, H, A, and G, because they are all related by an appropriate Legendre transform as shown in the following table. The constraints on the derivative are important. For example, (∂U/∂ni)P, T, nj ≠ i in Eqn. 10.36 is not equal to (∂U/∂ni)S, V, nj ≠ i = μi in the first line of the table.
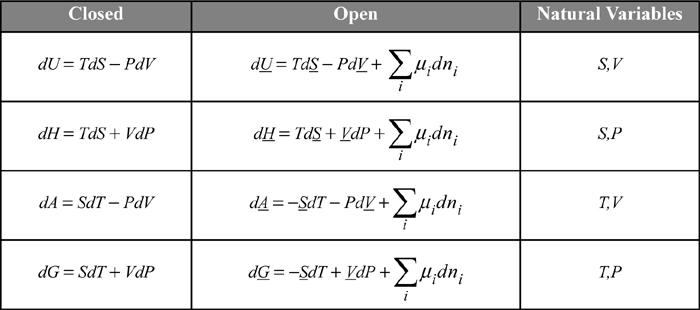
The open systems equations can be developed using the energy and entropy balances from the early chapters as shown in an online supplement.
Equilibrium Criteria
For equilibrium at constant T and P, the Gibbs energy is minimized and mathematically the minimum means dG = 0 at equilibrium. Therefore, Eqn. 10.38 is equal to zero at a minimum, since dT and dP are zero, and for a closed system all dni are zero. Thus,
This equation applies to whatever system we define. Suppose we define our system to consist of two components (e.g,. EtOH + H2O) distributed between two phases (e.g., vapor and liquid), dG = dGL + dGV = 0, and at constant T and P, the moles may redistribute between the two phases, by Eqn. 10.40 for both phases:
But if component 1 leaves the liquid phase then it must enter the vapor phase (and similarly for component 2) because the overall system is closed.
The only way to make this equal to zero in general is:
Setting the chemical potentials and T and P in each of the phases equal to each other provides a set of constraints (simultaneous equations) which may be solved for phase compositions provided we know the dependency of the chemical potentials on the phase compositions. Suppose the functions GL (x,T,P) and GV (y,T,P) are available for a binary system. Then
which gives four equations with four unknowns (x1, x2, y1, y2) that we can solve, in principle.11 The first two equations are simply the equivalency of chemical potentials in the two phases.
Chemical Potential of a Pure Fluid
In Chapter 9, we showed the equilibrium constraint for a pure fluid is equality of the molar Gibbs energy for each of the phases (cf. Eqn. 9.3). How does this relate to Eqn. 10.44?
For a pure fluid, there is only one component, so dni = dn, and since G(T,P) is intensive, then n(∂G/∂n)T,P = 0. Also (∂n/∂ni)T,P = 1 by Eqn. 6.13. Therefore,
That is, the chemical potential of a pure fluid is simply the molar Gibbs energy. Pure components can be considered as a special case of the same general statement of the equilibrium constraint.
Component Fugacity
We introduced fugacity in Chapter 9. The chemical potential constraint is sufficient for solving any phase equilibrium problem, but the most popular engineering approach for actual computations makes use of the concept of fugacity. Fugacity is more “user-friendly” than “chemical potential” or “partial molar Gibbs energy.” We have seen in Chapter 9 that the fugacity is the same as the pressure for an ideal gas, and that the fugacity is close to the vapor pressure for a liquid. Engineers use benchmarks such as these as guidelines for estimating fugacities and double-checking calculations. Fuga- comes from a Latin noun meaning flight, fleeing, or escape. The suffix -ity comes from a root meaning “character.” Thus, fugacity was invented to mean flight-character, commonly called “escaping tendency.” When phases are in equilibrium, the component moves (“escapes”) from the phase where it has the higher fugacity to the phase where it has the lower fugacity until the fugacities are equal in both phases.12
Let us generalize our pure component fugacity relations to apply to components in mixtures: At constant T, we defined RTdlnf ≡ dG (Eqn. 9.19) which can be generalized to define the fugacity of a component in a mixtures as
![]() Fugacity is another way to express the chemical potential that is used more widely in engineering than chemical potential.
Fugacity is another way to express the chemical potential that is used more widely in engineering than chemical potential.
where ![]() is the fugacity of component i in a mixture and μi is the chemical potential of the component. In the limit as the composition approaches purity, these properties become equal to the pure component values. A caret is used in the symbol for the fugacity of a component. The component fugacity is not a partial molar property, so the overbar cannot be used.
is the fugacity of component i in a mixture and μi is the chemical potential of the component. In the limit as the composition approaches purity, these properties become equal to the pure component values. A caret is used in the symbol for the fugacity of a component. The component fugacity is not a partial molar property, so the overbar cannot be used.
![]() Carets (^) are used to denote component properties in mixtures for f while without a caret the property is the pure component f. When working with μ, the meaning is inferred from the context of the situation.
Carets (^) are used to denote component properties in mixtures for f while without a caret the property is the pure component f. When working with μ, the meaning is inferred from the context of the situation.
Equality of Fugacities as Equilibrium Criteria
The equality of chemical potentials at equilibrium can easily be reinterpreted in terms of fugacity in a manner analogous to our methods for pure components from Eqn. 10.44:
By integrating Eqn. 10.46 as a function of composition at fixed T from a state of pure i to a mixed state, we find
where μi,pure and fi are for the pure fluid at the system temperature. Writing an analogous expression for the liquid phase, and equating the chemical potentials using Eqn. 10.47, we find
Note: Eqn. 10.47 or 10.50 becomes the starting point for all phase-equilibrium calculations. Therefore, we need to develop the capability to calculate chemical potentials or fugacities of components in vapor, liquid, and solid mixtures. Here we briefly introduce the framework for calculating the fugacities of components before we begin the direct calculations.
Eqn 10.50 does not look much like Raoult’s law, which was our motivation for exploring the thermodynamics of mixtures. To make this final connection between Raoult’s law and Eqn. 10.50, we need to understand how energy and volume affect component fugacities.
10.9. Mixture Properties for Ideal Gases
We have introduced the concepts of energy of mixing, enthalpy of mixing, and volume of mixing in Section 3.4. We can now relate the mixing behavior to the partial molar properties. The partial molar quantities for ideal gases must be the same as the pure component properties.
Entropy for an ideal-gas mixture is more complicated because, as shown in Chapter 4, even systems of fixed total energy have an entropy change associated with mixing due to the distinguishability of the components. The entropy of an ideal gas is calculated by the sum of the entropies of the components plus the entropy of mixing as given in Chapter 4:
Therefore, the entropy of mixing is nonzero and positive:
and the partial molar entropy is
The Gibbs energy and the fugacity will be at the core of phase equilibria calculations. The Gibbs energy of an ideal gas is obtained from the definition, G ≡ H – TS. Using Hig an Sig from above,
Therefore, the Gibbs energy of mixing is nonzero and negative:
The chemical potential of a component is given by Eqn. 10.39 and taking the derivative of Eqn. 10.55,
The derivative is most easily seen by expanding the logarithm before differentiation, ln yi = ln ni – ln n. Then,
Therefore, we find the chemical potential of an ideal-gas component:
By Eqn. 10.48, using Eqn. 10.59 and Eqn. 10.45,
By Eqn. 9.22, ![]() , resulting in the fugacity of an ideal-gas component:
, resulting in the fugacity of an ideal-gas component:
Therefore, the fugacity of an ideal-gas component is simply its partial pressure, yiP. This makes the ideal-gas fugacity easy to quantify rapidly for engineering purposes. One of the goals of the calculations that will be pursued in Chapter 15 is the quantification of the deviations of the fugacity from ideal-gas values quantified by the component fugacity coefficient.
![]() The fugacity of a component in an ideal-gas mixture is particularly simple; it is equal to the yiP, the partial pressure!
The fugacity of a component in an ideal-gas mixture is particularly simple; it is equal to the yiP, the partial pressure!
10.10. Mixture Properties for Ideal Solutions
Ideal solutions are similar to ideal-gas mixtures, but they to not follow the ideal-gas law. The internal energy and enthalpy for ideal solutions were introduced in Section 3.5. Since these properties are additive, the partial molar properties are equal to the pure component properties,
As for the entropy change of mixing, the loss of order due to mixing is unavoidable, even for ideal solutions. During our consideration of the microscopic definition of entropy, we derived a general expression for the ideal entropy change of mixing, Eqn. 4.8.
Although we derived Eqn. 4.8 for mixing ideal gases, it also provides a reasonable approximation for mixing liquids of equal-sized molecules. The reason is that changes in entropy are related to the change in accessible volume. Even though a significant volume is occupied by the molecules themselves in a dense liquid, the void space in one liquid is very similar to the void space in another liquid if the molecules are similar in size and polarity. That means that the accessible volume for each component doubles when we mix equal parts of two equal-sized components. That is essentially the same situation that we had when mixing ideal gases. The partial molar entropy of mixing is
Given the effect of mixing on these two properties, we can derive the effect on other thermodynamic properties, which has the same formula as that found for ideal gases:
The general relationship for ΔGmix gives a relationship for fugacity. We can extend our definition of the enthalpy of mixing to the Gibbs energy of mixing,
But by using Eqns. 10.42 and 10.48,
Thus, comparing Eqns. 10.67 and 10.65, for an ideal solution,  .
.
By comparing the relations in the logarithms, we obtain the Lewis-Randall rule for ideal solutions:
10.11. The Ideal Solution Approximation and Raoult’s Law
By our equilibrium constraint,
By our ideal solution approximation in both phases, the equilibrium criteria becomes
Now we need to substitute the expressions for fiV and fiL that we developed in Chapter 9. The fugacity of the pure vapor comes from Eqn. 9.25:
The fugacity of the liquid comes from Eqn. 9.39:
Combining Eqns. 10.70–10.72,

Writing in terms of the Ki ratio,
Note: at reasonably low pressures,
resulting in Raoult’s Law,
Raoult’s law is only valid for molecularly similar components; ideal behavior is demonstrated in the Figs. 10.2 and 10.3 because of careful selection of molecularly similar binary pairs. If we mixed methanol from Fig. 10.2(a) and benzene from Fig. 10.3(c), the resultant system would be very non-ideal.
10.12. Activity Coefficient and Fugacity Coefficient Approaches
The discussion in Sections 10.8–10.11 sets the stage for the next few chapters. The principles discussed here form the basis for these chapters and a thorough understanding facilitates rapid understanding of the extensions. There are two main approaches to modeling nonideal fluids. They differ in the way that they treat the fugacities in the vapor and liquid phases. The first approach is to model deviations from ideal solution behavior in the liquid phase, using activity coefficients, which is covered in Chapters 11 through 14. When the vapors are nonideal, the vapor phase fugacities are modeled with an equation of state, an approach that usually requires a computer. As discussed for pure fluids, liquid phases may also be modeled with an equation of state by simply selecting the liquid root. The EOS approach is discussed in Chapter 15.
The presentation has been organized according to a hierarchical approach. First and foremost, it is necessary to recognize that deviations from Raoult’s law can significantly alter the outlook on chemical processing. We introduce the activity approach for handling nonideal solutions in Chapter 11, and then extend to more complex models in Chapters 12 and 13. If you prefer a “one-size-fits-all” approach that can be applied to extremes of temperature, pressure, and component differences (e.g., CH4 + eicosane at oil reservoir conditions) then you may want to study Chapter 15 sooner. The EOS approach must be handled carefully for hydrogen bonding components, however, as discussed in Chapter 19. We provide more coverage than can typically be incorporated into a single undergraduate course, so instructors need to be selective about which models to cover. Nevertheless, the principles from one approach typically extend to other approaches and by focusing on a solid understanding of the principles for the sections studied, the reader should be able to extend them when the need arises.
10.13. Summary
The concepts in this chapter are relatively simple but far-reaching. A simple extension of the chain rule to multicomponent systems led to the equilibrium constraint for multicomponent multiphase equilibria. A simple application of the entropy of mixing derived in Chapter 4 led to the ideal solution model, Gibbs energy for a component in a mixture, and fugacity for a component in a mixture. This simple solution model enabled us to demonstrate the computational procedures for dew points, bubble points, and flashes.
In the remaining chapters of Unit III we proceed in a manner that is extremely similar. We propose a solution model and apply the equilibrium constraint to derive an expression for the K-ratios. Then we follow exactly the same computational procedures as developed here. The primary difference is the increasing level of sophistication incorporated into each solution model. Thus, the chapters ahead focus increasingly on the detailed description of the molecular interactions and the impacts of assumptions on the accuracy of the resultant solution models.
In this context, this chapter represents one iteration in the typical sequence of “observe, predict, test, and evaluate.” We observed that isothermal mixtures boil at higher pressures when more volatile components were present. We predicted that the bubble pressure varies linearly in mole fraction between the vapor pressures of the components (Raoult’s law). We tested these predictions by checking the linearity of several mixtures. We evaluated the assumptions implicit in Raoult’s law by extending the fundamental thermodynamic principles to mixtures. Successive iterations involve repeating this sequence, following up on clues from the previous evaluation.
Important Equations
We defined the K-ratio.
Raoult’s law is an important equation, but we have also seen that it has limited applicability.
We developed methods to calculate bubble, dew, and flash conditions summarized in Table 10.1 on page 373. We developed the relation for the relative volatility,
We discussed how the relative volatility varies dramatically with composition in an azeotropic system, approaching 1 at the azeotrope, and creating challenges. These variations undermine the utility of Raoult’s law and the use of shortcut design equations for azeotropic systems.
For phase equilibria, including liquid-liquid equilibria, the fugacities of a component are equal,
where α and β indicate different phases, whether vapor, liquid(s), or solid. This is the starting point throughout Unit III. As we applied the generalized approach, we found
and for an ideal solution,
Two final equations that form the basis for future derivations are
Through these equations, we can infer the fugacities of components in any solution, no matter how complex, by building a model for Gibbs energy. This is the subject of upcoming chapters. Models of the Gibbs energy may range from crudely empirical to sophisticated molecular analyses.
10.14. Practice Problems
P10.1. The stream from a gas well consists of 90 mol% methane, 5 mol% ethane, 3 mol% propane, and 2 mol% n-butane. This stream is flashed isothermally at 233 K and 70 bar. Use the shortcut K-ratio method to estimate the L/F fraction and liquid and vapor compositions. (ANS. L/F = 0.181)
P10.2. An equimolar mixture of n-butane and n-hexane at pressure P is isothermally flashed at 373 K. The liquid-to-feed ratio is 0.35. Use the shortcut K-ratio method to estimate the pressure and liquid and vapor compositions. (ANS. P = 0.533 MPa, xC6 = 0.78)
P10.3. A mixture of 25 mol% n-pentane, 45 mol% n-hexane, and 30 mol% n-heptane is flashed isothermally at 365.9 K and 2 bar. Use the shortcut K-ratio method to estimate the L/F fraction and liquid and vapor compositions. (ANS. L/F = 0.56)
P10.4. A mixture containing 15 mol% ethane, 35 mol% propane, and 50 mole% n-butane is isothermally flashed at 9 bar and temperature T. The liquid-to-feed ratio is 0.35. Use the shortcut K-ratio method to estimate the pressure and liquid and vapor compositions. (ANS. 319.4 K, xC4 = 0.74)
10.15. Homework Problems
10.1. For a separations process it is necessary to determine the VLE compositions of a mixture of ethyl bromide and n-heptane at 30°C. At this temperature the vapor pressure of pure ethyl bromide is 0.7569 bar, and the vapor pressure of pure n-heptane is 0.0773 bar. Calculate the bubble pressure and the composition of the vapor in equilibrium with a liquid containing 47.23 mol% ethyl bromide assuming ideal solution behavior. Compare the calculated pressure to the experimental value of 0.4537 bar.
10.2. Benzene and ethanol (e) form azeotropic mixtures. Prepare a y-x and a P-x-y diagram for the benzene-ethanol system at 45°C assuming the mixture is ideal. Compare the results with the experimental data tabulated below of Brown and Smith, Austral. J. Chem. 264 (1954). (P in the data table is in bar.)

10.3. The following mixture of hydrocarbons is obtained as one stream in a petroleum refinery on a mole basis: 5% ethane, 10% propane, 40% n-butane, 45% isobutane. Assuming the shortcut K-ratio model: (a) compute the bubble point of the mixture at 5 bar; (b) compute the dew point of the mixture at 5 bar; (c) find the amounts and compositions of the vapor and liquid phases that would result if this mixture were to be isothermally flash vaporized at 30°C from a high pressure to 5 bar.
10.4. Consider a mixture of 50 mol% n-pentane and 50 mol% n-butane at 14 bar.
a. What is the dew-point temperature? What is the composition of the first drop of liquid?
b. At what temperature is the vapor completely condensed if the pressure is maintained at 14 bar? What is the composition of the last drop of vapor?
10.5. A 50 mol% mixture of propane(1) and n-butane(2) enters an isothermal flash drum at 37°C. If the flash drum is maintained at 0.6 MPa, what fraction of the feed exits as liquid? What are the compositions of the phases exiting the flash drum? Work the problem in the following two ways.
a. Use Raoult’s law (use the Peng-Robinson equation to calculate pure component vapor pressures).
b. Assume ideal mixtures of vapor and liquid. (Use the Peng-Robinson equation to obtain fsat for each component.)
10.6. A mixture of 55 mol% ethanol in n-propanol is at 0.2MPa and 80°C at 70 mol/s. The stream is fed to a adiabatic flash drum. Calculate the outlet stream flow rates, temperatures, and compositions at 0.05MPa.
a. Use the path of Fig. 2.6(a).
b. Use the path of Fig. 2.6(c).
10.7. An equimolar ternary mixture of acetone, n-butane, and ammonia at 1 MPa is to be flashed. List the known variables, unknown variables, and constraining equations to solve each of the cases below. Assume ideal solution thermodynamics and write the flash equations in terms of K-ratios, with the equations for calculating K-ratios written separately.
a. Bubble temperature
b. Dew temperature
c. Flash temperature at 25 mol% vapor.
d. Raised to midway between the bubble and dew temperature, then adiabatically flashed
10.8. Tank A is rapidly half-filled with volatile hydrocarbon. Tank B is 10 times as large and rapidly half-filled with the same hydrocarbon. Initially the gas space can be considered to be free of volatile organic and at the same pressure. The tanks are then closed. The tanks warm 20°C and the pressure in both tanks goes up. After warming, does one tank have a higher pressure than the other, or are the final pressures the same? Show your result with equations. Your answer should be general; it should not depend on numerical calculations.
10.9. Above a solvent’s flash point temperature, the vapor concentration in the headspace is sufficient that a spark will initiate combustion; therefore, extreme care must be exercised to avoid ignition sources. Calculate the vapor phase mole fraction for the following liquid solvents using flash points listed, which were obtained from the manufacturer’s material safety data sheets (MSDS). The calculated vapor concentration is an estimate of the lower flammability limit (LFL). Assume that the headspace is an equilibrium mixture of air and solvent at 760 mmHg. The mole fraction of air dissolved in the liquid solvent is negligible for this calculation.
a. Methane, –187.8°C
b. Propane, –104.5°C
c. Pentane, –48.9°C
d. Hexane, –21.7°C
e. Ethanol, 12.7°C
f. 2-butanone, –5.6°C
g. Toluene, 4.4°C
h. m-xylene, 28.8°C
i. Ethyl acetate, –4.5°C
10.10. Solvent vessels must be purged before maintenance personnel enter in order to ensure that: (1) sufficient oxygen is available for breathing; (2) vapor concentrations are below the flash point; (3) vapor concentrations are below the Occupational Safety and Health Administration (OSHA) limits if breathing apparatus is not to be used. Assuming that a 8 m3 fixed-roof solvent tank has just been drained of all liquid and that the vapor phase is initially saturated at 22°C, estimate the length of purge necessary with 2 m3/min of gas at 0.1 MPa and 22°C to reach the OSHA 8-hr exposure limit.13
a. Hexane 500 ppm
b. 1-butanol 100 ppm
c. Chloroform 50 ppm
d. Ethanol 1000 ppm
e. Toluene 200 ppm
10.11. A pharmaceutical product is crystallized and washed with absolute ethanol. A 100 kg batch of product containing 10% ethanol by weight is to be dried to 0.1% ethanol by weight by passing 0.2 m3/min of 50°C nitrogen through the dryer. Estimate the rate (mol/min) that ethanol is removed from the crystals, assuming that ethanol exerts the same vapor pressure as if it were pure liquid. Based on this assumption, estimate the residence time for the crystals in the dryer. The dryer operates at 0.1 MPa and the vapor pressure of the pharmaceutical is negligible.
10.12. Benzyl chloride is manufactured by the thermal or photochemical chlorination of toluene. The chlorination is usually carried out to no more than 50% toluene conversion to minimize the benzal chloride formed. Suppose reactor effluent emissions can be modeled ignoring by-products, and the effluent is 50 mol% toluene and 50 mol% benzyl chloride. Estimate the emission of toluene and benzyl chloride (moles of each) when an initially empty 4 m3 holding tank is filled with the reactor effluent at 30°C and 0.1 MPa.
10.13. This problem explores emissions during heating of hexane(1) and toluene(2) in a tank with a fixed roof that is vented to the atmosphere through an open pipe in the roof. Atmospheric pressure is 760 mmHg. The tank volume is 2000 L, but the maximum operating liquid level is 1800 L. Determine the emissions of each VOC (in g) when the tank is heated.
a. The liquid volume is 1800 L, x1 = 0.5, Ti = 10°C, ΔT = 15°C.
b. The liquid volume is 1800 L, x1 = 0.5, Ti = 25°C, ΔT = 15°C.
c. The liquid volume is 1500 L, x1 = 0.5, Ti = 25°C, ΔT = 15°C.
d. The liquid volume is 1800 L, x1 = 1.0, Ti = 25°C, ΔT = 15°C.
e. Explain why the ratio [(emission of toluene in part (b))/(emission of toluene in part (a))] is different from the corresponding ratio of hexane emissions.
10.14. Use Raoult’s law to estimate the flash point temperature for the following equimolar liquid mixtures in an air atmosphere at 750 mmHg total pressure:
a. Pentane (LFL = 1.5%) and hexane (LFL = 1.2%)
b. Methanol (LFL = 7.3%) and ethanol (LFL = 4.3%)
c. Benzene (LFL = 1.3%) and toluene (LFL = 1.27%)
10.15. Go to www.csb.gov and watch a video assigned by your instructor. For the substance involved, look up the LFL. Use Raoult’s law to estimate the flash point temperature and compare it with a literature value. For the scenario in the video, offer an explanation of how easy or difficult is was to reach the LFL under the conditions, and comment on the recommendations of the CSB.