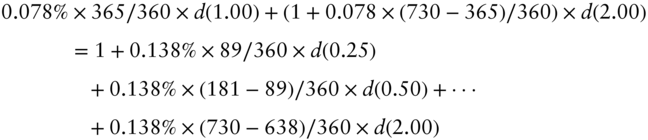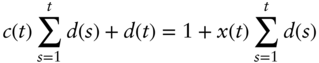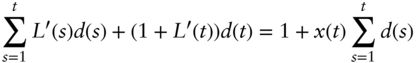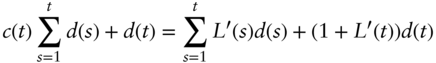APPENDIX TO CHAPTER 13
Interest Rate Swaps
A13.1 PRICING A EURIBOR SWAP AS OF FEBRUARY 24, 2022
This section prices a two‐year fixed‐for‐floating swap, where the floating rate is three‐month Euribor. The inputs are the term structure of €STR OIS given in Table A13.1, the two‐year Euribor swap rate of 0.078%, and the two‐year €STR–Euribor basis swap spread of 0.138%. All cash flows are assumed to follow the actual/360 convention, and all of the relevant dates are assumed to be business days.
The OIS rates in the fourth column of the table are observed in the market. The discount factors are calculated by setting the present value of the fixed payments on each OIS (including the fictional notional amount at maturity) equal to par, which is the value of the floating legs that pay compounded daily €STR. Letting ![]() denote the discount factor for
denote the discount factor for ![]() years, the equations determining the discount factors, along the same lines as for SOFR swaps explained in Chapter 2, are the following,
years, the equations determining the discount factors, along the same lines as for SOFR swaps explained in Chapter 2, are the following,
TABLE A13.1 €STR OIS Rates as of February 24, 2022.
| Term | Term | Term | Rate | Discount | Fwd Rate |
|---|---|---|---|---|---|
| (years) | (date) | (days) | (%) | Factor | (%) |
| 0.25 | 05/24/2022 | 89 | −0.5695 | 1.0014099 | −0.1408 |
| 0.50 | 08/24/2022 | 181 | −0.5580 | 1.0028134 | −0.1400 |
| 0.75 | 11/24/2022 | 273 | −0.5110 | 1.0038902 | −0.1073 |
| 1.00 | 02/24/2023 | 365 | −0.4380 | 1.0044606 | −0.0568 |
| 1.25 | 05/24/2023 | 454 | −0.3380 | 1.0042784 | 0.1081 |
| 1.50 | 08/24/2023 | 546 | −0.2330 | 1.0035455 | 0.0730 |
| 1.75 | 11/24/2023 | 638 | −0.1400 | 1.0024888 | 0.1054 |
| 2.00 | 02/24/2024 | 730 | −0.0600 | 1.0012201 | 0.1267 |

Solving this set of equations gives the discount factors in Table A13.1. The resulting forward rates are shown in the table as well but are not needed for the remaining calculations. In any case, with these discount factors, the two‐year Euribor swap rate of 0.078% and the two‐year €STR versus three‐month Euribor basis swap spread of 0.138% are related by equating the present value of the fixed side of the Euribor swap payments (including the fictional notional amount) to one (i.e., the value of floating €STR, including the fictional notional amount) plus the present value of the basis swap spread payments. Mathematically,
Note that Equation (A13.2) is the pricing condition. Given the 0.078% swap rate, it can be used to solve for the 0.138% basis swap spread. Or, conversely, given the 0.138% basis swap spread, it can be used to solve for the 0.078% swap rate.
A13.2 TWO‐CURVE PRICING
For the purposes of this section, assume for simplicity that payments are annual at times ![]() . For ease of exposition, say that the risk‐free rate index is €STR and that the non‐risk‐free rate index is Euribor. Given a set of discount factors,
. For ease of exposition, say that the risk‐free rate index is €STR and that the non‐risk‐free rate index is Euribor. Given a set of discount factors, ![]() , derived from €STR OIS; a set of Euribor swap rates,
, derived from €STR OIS; a set of Euribor swap rates, ![]() ; and €STR versus Euribor basis swap spreads,
; and €STR versus Euribor basis swap spreads, ![]() , the fair pricing conditions for the Euribor swaps, discussed in the text and the previous section are, for every
, the fair pricing conditions for the Euribor swaps, discussed in the text and the previous section are, for every ![]() ,
,
Now define a set of adjusted Euribor forward rates, ![]() , such that the present values of the floating legs of the Euribor swaps equal their correct values, which are given by the right‐hand side of (A13.3),
, such that the present values of the floating legs of the Euribor swaps equal their correct values, which are given by the right‐hand side of (A13.3),
Given the basis swap spreads, Equation (A13.4) could be used to solve for all of the adjusted Euribor forward rates, one at a time, starting with ![]() and continuing through to
and continuing through to ![]() . These
. These ![]() could then be used to price payments that depend on Euribor. However, noticing that the right‐hand sides of Equations (A13.3) and (A13.4) are the same, these two equations can be combined,
could then be used to price payments that depend on Euribor. However, noticing that the right‐hand sides of Equations (A13.3) and (A13.4) are the same, these two equations can be combined,
But given all of the swap rates, ![]() , Equation (A13.5) can be used iteratively to solve for the
, Equation (A13.5) can be used iteratively to solve for the ![]() . In other words, so long as the Euribor swaps are priced fairly relative to €STR OIS, there is no need to know the basis swap spreads.
. In other words, so long as the Euribor swaps are priced fairly relative to €STR OIS, there is no need to know the basis swap spreads.
In summary, then, the two‐curve methodology for pricing Euribor swaps is as follows. First, solve for the adjusted forward rates, ![]() , as just described. Second, project those adjusted forward rates as future Euribor floating rates to set floating‐leg payments. Third, discount both fixed‐ and floating‐leg payments using the €STR discount factors.
, as just described. Second, project those adjusted forward rates as future Euribor floating rates to set floating‐leg payments. Third, discount both fixed‐ and floating‐leg payments using the €STR discount factors.