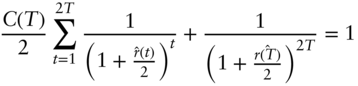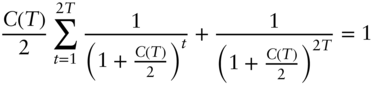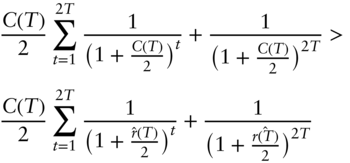APPENDIX TO CHAPTER 2
Swap, Spot, and Forward Rates
A2.1 CONTINUOUS COMPOUNDING
Equation (2.7) gives the proceeds of investing 
for 
periods at the rate 
, which is compounded 
times per year. By the definition of 
, there are 
periods over 
years. Therefore, with 
, (2.7) becomes,
Under continuous compounding, interest is paid every instant, so that the proceeds of an investment that is continuously compounded over 
years grows to the limit of Equation (A2.1) as 
approaches infinity. Taking the logarithm of (A2.1) and rearranging terms,
Using l'Hôpital's rule, the limit of the right‐hand side of (A2.2) as 
becomes large is 
. Hence, the limit of (A2.1) is 
, where 
is the base of the natural logarithm. Therefore, if interest is continuously compounded at the rate 
, an investment of one unit of currency will grow after 
years to,
Equivalently, the present value of one unit of currency to be received in 
years is,
This section now defines discount factors, spot rates, and forward rates under continuous compounding. Let 
be the 
‐year continuously compounded spot rate. Let 
be the forward rate from 
to 
, and define 
to be the continuously compounded forward rate at time 
, that is, the limit of 
as 
approaches zero.
By Equation (A2.4), spot rates and discount factors are related such that,
Linking forward rates and spot rates is the continuously compounded analog of Equation (2.21),
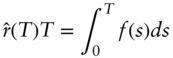
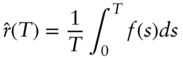
To link forward rates and discount factors, note that the continuously compounded analogue of Equation (2.20) is,
Then substitute from Equation (A2.5) for each of the two spot rates and rearrange terms to get,
Then take the natural logarithm of both sides and rearrange terms,
Finally, take the limit of both sides of this equation, recognizing that the limit of the right‐hand side is the derivative of 
, to obtain,
where 
is the derivative of the discount function with respect to term.
A2.2 RELATIONSHIPS BETWEEN SWAP OR PAR, SPOT, AND FORWARD RATES
This section will work with semiannually compounded rates, though it could easily be cast in terms of other compounding intervals.
Approximation: The 
‐year spot rate is approximately equal to the average of all forward rates to year 
.
Start from Equation (2.21), noting that, because interest rates themselves are small numbers, the product of two or more interest rates is particularly small. To illustrate, take the case of the one‐year spot rate, though the argument generalizes easily to longer‐term rates,
where the approximation from (A2.14) to (A2.15) comes from dropping the terms that multiply two rates.
Proposition 1:
Proof: Define 
as the left‐hand side of (A2.16). Then,
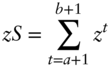
and it follows that,
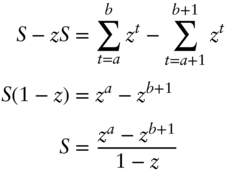
as was to be shown.
Proposition 2: If the term structure of spot rates is flat, then the term structure of par rates is flat at that same rate.
Proof: Denote the semiannually compounded par rate of maturity 
as 
. If spot rates are flat at the rate 
, then, by definition of 
,
Applying Equation (A2.16) of Proposition 1 with 
,
But solving (A2.18) for 
shows that 
. Hence, the term structure of par rates is flat at 
, as was to be shown.
Proposition 3: 
if and only if 
.
Proof: The condition 
is equivalent to,
But, using Equation (2.20) to rewrite the left‐hand side of (A2.19),
as was to be shown.
Proposition 4: 
if and only if 
.
Proof: Reverse the inequalities in the proof of Proposition 3.
Proposition 5: If 
, then 
.
Proof: By the definition of the par rate, 
,
It is easy to show from Equation (A2.16), setting 
, that,
And, because the term structure of spot rates is assumed to be increasing,
Note that the spot rates in the summation on the top line are 
, while those in the summation in the bottom line are all 
.
Now, because the left‐hand sides of Equations (A2.22), (A2.23), and (A2.24) are all equal to one, the left‐hand side of (A2.23) can replace the left‐hand side of (A2.24), that is,
which implies that 
, which was to be proved.
Proposition 6: If 
, then 
.
Proof: Reverse the inequalities of Equations (A2.24) and (A2.25) in the previous proof to conclude that 
, as was to be proved.