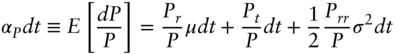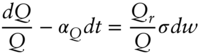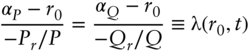APPENDIX TO CHAPTER 8
Expectations, Risk Premium, Convexity and the Shape of the Term Structure
This appendix proves Equation (8.18) along the lines of Ingersoll (1987).1 Assume that 
, the single, instantaneous rate factor, follows the process,
Let 
be the full price of some security that depends on 
and time. Then, by Ito's lemma,
where 
, 
, and 
denote the partial first derivatives with respect to 
and 
and the second partial derivative with respect to 
. Dividing both sides of (A8.2) by 
, taking expectations, and defining 
to be the expected return of the security,
Combining (A8.1), (A8.2), and (A8.3),
Because Equation (A8.4) applies to any security, it also applies to some other security 
,
Now consider the strategy of investing one unit of currency in security 
and 
in security 
. From Equations (A8.4) and (A8.5), the return on this portfolio is,
Note that terms with the random variable 
have fallen out of Equation (A8.6). This particular portfolio is chosen, in fact, so as to hedge completely the risk of 
with 
. In any case, because the portfolio has no risk, it must earn the instantaneous rate, 
,
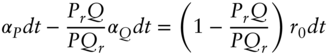
Rearranging terms,
Equation (A8.8) says that the expected return of any security above the instantaneous rate divided by its duration with respect to that rate must equal some function 
. This function cannot depend on any characteristic of the security, because (A8.8) is true for all securities. The function may depend, however, on the interest rate factor and time. Rewriting Equation (A8.8), for any security 
,
NOTE
- 1 Ingersoll, J. (1987), Theory of Financial Decision Making, Rowman & Littlefield.