A3.1 YIELD TO MATURITY FOR SETTLEMENT DATES OTHER THAN COUPON PAYMENT DATES

Equations (3.6), (3.7), and (3.8) express the relationship between price and yield to maturity when settlement is on a coupon payment date. This appendix generalizes this relationship to other settlement dates. First, because accrued interest is zero when settlement falls on a coupon payment date, the full price in the equations in the text do not include any accrued interest. In this section, however, because settlement can fall on other dates, is taken to include accrued interest.

Second, the market convention for discounting cash flows that do not occur in regular six‐month intervals, using a semiannually compounded rate, is as follows. Let denote the semiannually compounded yield, and let denote the fraction of a semiannual period until the next coupon payment. For example, if the next coupon payment is in one month, taken to mean one‐sixth of a semiannual period, then . By convention, then, the present value of a unit of currency at that time is,

(A3.1)

Note that, while reasonably intuitive, this convention cannot really be justified by the logic of compounding conventions. As discussed in the text, represents the final proceeds of an investment of one unit of currency semiannually compounded times. There is no such interpretation for an exponent that is not a whole number of semiannual periods. In any case, continuing along these lines, the present value of a unit of currency to be paid after semiannual periods is,

(A3.2)

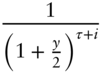
Finally, then, consider a bond with remaining coupon payments of , the first of which is paid after semiannual periods, the second after semiannual periods, the third after semiannual periods, etc., and the last, along with a principal payment of 100, after semiannual periods. Its price is given by,

(A3.3)

(A3.4)

(A3.5)

where (A3.5) can be derived from Equation (A2.16) in Appendix A2.2.

A3.2 YIELD TO MATURITY AND EX‐POST RETURNS

For simplicity, this section assumes annual coupons and annual compounding.

Proposition: A ‐year coupon bond priced at a yield of earns per year over years if its coupons are all reinvested at and if the bond's yield at the end of years is .

Proof: Let and be the prices of the bond at time 0 ( years to maturity) and after years ( years to maturity) when its yield is .

Starting with the definition of yield to maturity,

(A3.6)

(A3.7)

(A3.8)

(A3.9)

where (A3.7) simply multiplies both sides of (A3.6) by ; (A3.8) recognizes that the second line of (A3.7) is just , the price of the bond after years, with a remaining maturity of years and a yield of ; and (A3.9) simplifies terms.

By inspection, the right‐hand side of Equation (A3.9) is the ‐year return of the bond if all coupons are reinvested at and if the yield after years is . Breaking that down, the numerator gives the reinvested coupon payments at a yield of ; plus , the price of the bond after years if the yield is ; minus the initial price of the bond at the yield . Hence, the numerator divided by the initial price equals the ‐year return.

But if the right‐hand side of the bond is the ‐year return under the conditions stated, then, by the left‐hand side, that return is equivalent to earning per year for years.

Note that the proposition is not an “if and only if,” because it is possible – though very unlikely – to have some combination of returns on coupons and a final yield that also result in a holding‐period return of per year.

A3.3 REALIZED FORWARD SCENARIO

For simplicity, this section assumes annual coupons and annual compounding.

Proposition: Under the realized forward scenario, the ‐year return of a ‐year coupon, with coupon income reinvested at the initial forward rates , ,…, is the same as from rolling over a unit of currency at those forward rates.

Proof: Let and be the prices of the bond at time 0 ( years to maturity) and after years ( years to maturity) under the realized forward scenario.

Starting with the definition of forward rates,

(A3.10)

(A3.11)

(A3.12)

(A3.13)

where (A3.11) simply multiplies both sides of (A3.10) by ; (A3.12) recognizes that the second and third lines of (A3.11) are , the price of the bond after years, with discounting under the assumption of realized forwards; and (A3.13) simplifies terms.

By inspection, the right‐hand side of Equation (A3.13) is the ‐year return of the bond if all coupons are reinvested at the short‐term rate of the realized forward scenario and if, after years, the bond is priced under that scenario. But if the right‐hand side is the bond's ‐year return under the conditions stated, then, by the left‐hand side, that return is equivalent to rolling over a unit of currency at the initial forward rates for years.

Corollary: Under the realized forward scenario, the one‐year return of any coupon bond is the short‐term rate, .

Proof: Following the proof of the previous proposition with , Equation (A3.13) becomes,

(A3.14)

which was to be proved.