1.4. Sampling from Multivariate Normal Populations

Suppose we have a random sample of size n, say y1, ..., yn, from the p dimensional multivariate normal population N_p(μ, Σ). Since y1, ..., yn are independently and identically distributed (iid), their sample mean

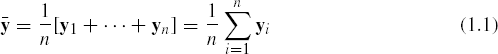
is also normally distributed as N_p(μ, Σ/n). Thus, is an unbiased estimator of μ. Also, observe that has a dispersion matrix which is a multiple of the original population variance-covariance matrix. These results are straightforward generalizations of the corresponding well known univariate results.

The sample variance of the univariate normal theory is generalized to the sample variance-covariance matrix in the multivariate context. Accordingly, the chi-square distribution is generalized to a matrix distribution known as the Wishart distribution.

The p by p sample variance-covariance matrix is obtained as

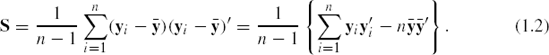
The matrix S is an unbiased estimator of Σ. Note that S is a p by p symmetric matrix. Thus, it contains only different random variables.

Let

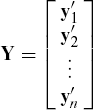
be the n by p data matrix obtained by stacking y1′, ..., yn′ one atop the other. Let In stand for an n by n identity matrix and 1_n be an n by 1 column vector with all elements as 1. Then, in terms of Y, the sample mean can be written as

and the sample variance-covariance matrix can be written as

It is known that (n - 1)S follows a p-(matrix) variate Wishart distribution with (n - 1) degrees of freedom and expectation (n - 1)Σ. We denote this as (n - 1)S ~ W_p(n - 1, Σ). Also, S is an unbiased estimator of Σ (as mentioned earlier, this is always true regardless of the underlying multivariate normality assumption and consequently, without any specific reference to the Wishart distribution).

Since (n - 1)S has a Wishart distribution, the sample variance-covariance matrix S possesses certain other important properties. Many of these properties are used to obtain the distributions of various estimators and test statistics. Some of these properties are listed as follows.

• (n - 1)s_ii/σ_ii ~ χ²(n - 1), i = 1, ..., p.

• Let

S_11·2 = S₁₁ - S₁₂S⁻¹₂₂S₂₁, Σ_11·2 = Σ₁₁ - Σ₁₂ Σ⁻¹₂₂Σ₂₁, S_22.1 = S₂₂ - S₂₁S⁻¹₁₁S₁₂ and Σ_22.1 = Σ₂₂ - Σ₂₁Σ⁻¹₁₁Σ₁₂, then

(a) (n - 1)S₁₁ ~ W_p1((n - 1), Σ₁₁).

(b) (n - 1)S₂₂ ~ W_p2((n - 1), Σ₂₂).

(c) (n - 1)S_11·2 ~ W_p1((n - p + p₁ - 1), Σ_11·2).

(d) (n - 1)S_22.1 ~ W_p2((n - p₁ - 1), Σ_22.1).

(e) S₁₁ and S_22.1 are independently distributed.

(f) S₂₂ and S_11·2 are independently distributed.

• Let sⁱⁱ and σⁱⁱ be the i^th diagonal elements of S⁻¹ and Σ⁻¹ respectively, then (n - 1)σⁱⁱ/sⁱⁱ ~ χ²(n - p).

• Let c ≠ 0 be an arbitrary but fixed vector, then

  
  

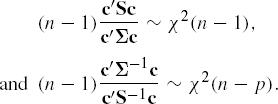
• Let H be an arbitrary but fixed k × p matrix (k ≤ p), then

  (n - 1)HSH′ ~ W_k (n - 1, HΣH′).

  In principle, k can also be greater than p but in such a case, the matrix (n - 1)HSH′ does not admit a probability density.

As a consequence of the above result, if we take k = p and H = G′ where Σ⁻¹ = GG′, then (n - 1)S* = (n - 1)G′SG ~ W_p(n - 1, I).

In the above discussion, we observed that the Wishart distribution arises naturally in the multivariate normal theory as the distribution of the sample variance-covariance matrix (of course, apart from a scaling by (n - 1)). Another distribution which is closely related to the Wishart distribution and is useful in various associated hypothesis testing problems is the matrix variate Beta (Type 1) distribution. For example, if A₁ and A₂ are two independent random matrices with A₁ ~ W_p(n₁ - 1, Σ) and A₂ ~ W_p(n₂, Σ), then B = (A₁ + A₂)^−½A₁(A₁ + A₂)^−½ follows a matrix variate Beta Type 1 distribution, denoted by B_p( Type 1). Similarly, B* = A₂^−½ A₁A₂^−½ follows B_p( Type 2), a matrix variate Beta Type 2 (or a matrix variate F apart from a constant) distribution. The matrices A₂^−½ and (A₁ + A₂)^−½ respectively are the symmetric "square root" matrices of A⁻¹₂ and (A₁ + A₂)⁻ in the sense that A⁻¹₂ = (A₂)^−½(A₂)^−½ and (A₁ + A₂)⁻¹ = (A₁ + A₂)^−½ (A₁ + A₂)^−½. The eigenvalues of the matrices B and B* appear in the expressions of various test statistics used in hypothesis testing problems in multivariate analysis of variance.

Another important fact about the sample mean and the sample variance-covariance matrix S is that they are statistically independent under the multivariate normal sampling theory. This fact plays an important role in constructing test statistics for certain statistical hypotheses. For details, see Kshirsagar (1972), Timm (1975), or Muirhead (1982).