5.4. Digital Signatures

Suppose an entity (Alice) is required to be bound to some electronic data (like messages or documents or keys). This binding is achieved by Alice digitally signing the data in such a way that no party other than Alice would be able to generate the signature. The signature should also be such that any entity can easily verify that it was Alice who generated the signature. Digital signatures can be realized using public-key techniques. The entity (Alice) generating a digital signature is called the signer, whereas anybody who wants to verify a signature is called a verifier.

We have seen in Section 5.2 how the encryption and decryption transforms f_e, f_d achieve confidentiality of sensitive data. If the set of all possible plaintext messages is the same as the set of all ciphertext messages and if f_e and f_d are bijective maps on that set, then the sequence of encryption and decryption can be reversed in order to realize a digital signature scheme. In order to sign m, Alice uses her private key d and the transform f_d to generate s = f_d(m, d). Any party who knows the corresponding public key e can recover m as m = f_e(s, e). This is broadly how a signature scheme works. Depending on how the representative m is generated from the message M that Alice wants to sign, signature schemes can be classified in two categories.

Signature scheme with message recovery

In this case, one takes m = M. Verification involves getting back the message M. If M is assumed to be (the encoded version of) some human-readable text, then the recovered M = f_e(s, e) will also be human-readable. If s is forged, that is, if a private key d′ ≠ d has been used to generate s′ = f_d(m, d′), then verification using Alice’s public key yields m′ = f_e(s′, e), and typically m′ ≠ m, since d′ and e are not matching keys. The resulting message m′ will, in general, make little or no sense to a human reader. If m is not a human-readable text, one adds some redundancy to it before signing. A forged signature yields m′ during verification, which, with high probability, is expected not to have this redundancy.

Attractive as it looks, it is not suitable if M is a long message. In that case, it is customary to break M into smaller pieces and sign each piece separately. Since public-key operations are slow, signature generation (and also verification) will be time-consuming, if there are too many pieces to sign (and verify). This difficulty is overcome using the second scheme described now.

Signature scheme with appendix

In this scheme, a short representative m = H(M) of M is first computed.^[2] The function H is usually chosen to be a hash function, that is, one which converts bit strings of arbitrary length to bit strings of a fixed length. H is assumed to be a public knowledge, that is, anybody who knows M can compute m. We also assume that H(M) can be computed fast for messages M of practical sizes. Alice uses the decryption transform on m to generate s = f_d(m, d). The signature now becomes the pair (M, s). A verifier obtains Alice’s public key e and checks if H(M) = f_e(s, e). The signature is taken to be valid if and only if equality holds. If a forger uses a private key d′ ≠ d, she generates a signature (M, s′), s′ = f_d(m, d′), on M and a verifier expects with high probability the inequality H(M) ≠ f_e(s′, e).

^[2] If M is already a short message, one may go for taking m = M. In order to promote uniform treatment, we assume that the function H is always applied for the generation of m. Use of H is also desirable from the point of security considerations (Exercise 5.15).

A kind of forgery is possible on signature schemes with appendix. Assume that Alice creates a valid signature (M, s), s = f_d(H(M), d), on a message M. The function H is certainly not injective, since its input space is much bigger (infinite) than its output space (finite). Suppose that Carol finds a message M′ ≠ M with H(M′) = H(M). In that case, the pair (M′, s) is a valid signature of Alice on the message M′, though it is not Alice who has generated it. (Indeed it has been generated without the knowledge of the private key d of Alice.) In order to foil such attacks, the function H should have second pre-image resistance. The first pre-image resistance and collision resistance properties of a hash functions also turn out to be important in the context of digital signatures. See Sections 1.2.6 and A.4 to know about hash functions.

We now describe some specific algorithms for (generating and verifying) digital signatures. Key pairs used for these algorithms are usually identical to those used for encryption algorithms of Section 5.2 and, therefore, we refrain from a duplicate description of the key-generation procedures. We focus our discussion only on signature schemes with appendix.

5.4.1. The RSA Digital Signature Algorithm

As in the RSA encryption scheme of Section 5.2.1, each entity generates an RSA modulus n = pq, which is the product of two distinct large primes p and q. A key pair consists of an encryption exponent e (the public key) and a decryption exponent d (the private key) satisfying ed ≡ 1 (mod φ(n)).

RSA signature generation involves a modular exponentiation in the ring .

Algorithm 5.32. RSA signature generation

Input: A message M to be signed and the signer’s private key (n, d). Output: The signature (M, s) on M. Steps: m := H(M).   /*  is the short representative of M */ s := md (mod n).

Signature generation can be speeded up if the parameters p, q, d₁ := d rem (p – 1), d₂ := d rem (q – 1) and h := q^–1 (mod p) are stored (secretly) in the private key. Now, one can use Algorithm 5.4 for signature generation.

The verification routine also involves a modular exponentiation in .

Algorithm 5.33. RSA signature verification

Input: A signature (M, s) and the signer’s public key (n, e). Output: Verification status of the signature. Steps: m := H(M).   /*  is the short representative of M */  (mod n). if  { Return “Signature verified”. } else { Return “Signature not verified”. }

Small values of e speed up RSA signature verification and are not known to make the scheme suffer from some special attacks. So the values of e like 3, 257 and 65,537 are quite recommended.

5.4.2. The Rabin Digital Signature Algorithm

As in the Rabin encryption algorithm, we choose two distinct large primes p and q of nearly equal sizes and take n = pq. The public key is n, whereas the private key is the pair (p, q). The Rabin signature scheme is based on the intractability of computing square roots modulo n in absence of the knowledge of the prime factors p and q of n.

Rabin signature generation involves finding a quadratic residue m modulo n as a representative of the message M and computing a square root of m modulo n.

Algorithm 5.34. Rabin signature generation

Input: A message M to be signed and the signer’s private key (p, q). Output: The signature (M, s) on M. Steps: m := H(M).          /*  is assumed to be a quadratic residue modulo n */ Compute a square root s1 of m modulo p. /* Algorithm 3.17 */ Compute a square root s2 of m modulo q. /* Algorithm 3.17 */ Compute satisfying s ≡ s1 (mod p) and s ≡ s2 (mod q). /* CRT */

Verification (Algorithm 5.35) involves a square operation in .

Algorithm 5.35. Rabin signature verification

Input: A signature (M, s) and the signer’s public key n. Output: Verification status of the signature. Steps: m := H(M). /* is a quadratic residue modulo n */ (mod n). if { Return “Signature verified”. } else { Return “Signature not verified”. }

5.4.3. The ElGamal Digital Signature Algorithm

The ElGamal signature algorithm is based on the intractability of computing discrete logarithms in certain groups G. For a general description, we consider an arbitrary (finite Abelian multiplicative) group G of order n. We assume that G is cyclic and that a generator g of G is provided. A key pair is obtained by selecting a random integer (the private key) d, 2 ≤ d ≤ n – 1, and then computing g^d (the public key). The hash function H is assumed to convert arbitrary bit strings to elements of . We further assume that the elements of G can be identified as bit strings (on which the hash function H can be directly applied). G (together with its representation), g and n are considered to be public knowledge and are not input to the signature generation and verification routines.

ElGamal signatures are generated as in Algorithm 5.36. The appendix consists of a pair .

Algorithm 5.36. ElGamal signature generation

Input: A message M to be signed and the signer’s private key d. Output: The signature (M, s, t) on M. Steps: Generate a random session key d′, 2 ≤ d′ ≤ n – 1. s := gd′. t := d′–1 (H(M) – dH(s)) (mod n).

The costliest step in the ElGamal signature generation algorithm is the exponentiation g^d′. Here, G is assumed to be cyclic and the exponent d′ to be O(n). We will shortly see modifications of the ElGamal scheme in which the exponent can be chosen to be much smaller, namely O(r), where r is a suitably large (prime) divisor of n.

In order to forge a signature, Carol can generate a random session key (d′, g^d′) and obtain s. For the computation of t, she requires the private key d of the signer. Conversely, if t (and d′) are available to Carol, she can easily compute the private key d. Thus, forging an ElGamal signature is equivalent to solving the DLP in G.

Each invocation of the ElGamal signature generation algorithm must use a new session key (d′, g^d′). If the same session key (d′, g^d′) is used to generate the signatures (M₁, s₁, t₁) and (M₂, s₂, t₂) on two different messages M₁ and M₂, then we have (t₁ – t₂)d′ ≡ H(M₁) – H(M₂) (mod n), whence d′ can be computed, provided that gcd(t₁ – t₂, n) = 1. If d′ is known, the private key d can be easily computed (see Exercise 5.6 for a similar situation).

ElGamal signature verification is described in Algorithm 5.37. This is based on the observation that for a (valid) ElGamal signature (M, s, t) on a message M we have . This verification calls for three exponentiations in G to full-size exponents. Working in a suitable (cyclic) subgroup of G makes the algorithm more efficient.

Algorithm 5.37. ElGamal signature verification

Input: A signature (M, s, t) and the signer’s public key gd. Output: Verification status of the signature. Steps: a1 := gH(M). a2 := (gd)H(s)st. if (a1 = a2) { Return “Signature verified”. } else { Return “Signature not verified”. }

ElGamal signatures use a congruence of the form A ≡ dB + d′C (mod n), and verification is done by checking the equality g^A = (g^d)^Bs^C. Our choice for A, B and C was A = H(M), B = H(s) and C = t. Indeed, any permutation of H(M), H(s) and t are acceptable as A, B, C. These give rise to several variants of the ElGamal scheme. It is also allowed to take as A, B, C any permutation of H(M)H(s), t, 1 or H(M)H(s), H(M)t, 1 or H(M)H(s), H(s)t, 1 or H(M)t, H(s)t, 1. Permutations of H(M)H(t), H(s), 1 or H(M), H(s)t, 1, on the other hand, are known to have security bugs. For any allowed combination of A, B, C, the choices ±A, ±B, ±C are also valid. For some other variants, see Horster et al. [132].

5.4.4. The Schnorr Digital Signature Algorithm

The Schnorr signature scheme is a modification of the ElGamal scheme and is faster than the ElGamal scheme, since it works in a subgroup of G generated by g of small order. We assume that r := ord g is a prime (though it suffices to have ord g possessing a suitably large prime divisor). We suppose further that the elements of G are represented as bit strings and that we have a hash function H that maps bit strings to elements of . A key pair now consists of an integer d (the private key), 2 ≤ d ≤ r – 1, and the element g^d (the public key).

Schnorr signature generation is described in Algorithm 5.38.

Algorithm 5.38. Schnorr signature generation

Input: A message M to be signed and the signer’s private key d. Output: The signature (M, s, t) on M. Steps: Generate a random session key pair (d′, gd′), 2 ≤ d′ ≤ r – 1. s := H(M‖gd′). /* Here ‖ denotes string concatenation */ t := d′ – ds (mod r).

Similar to the ElGamal scheme, the most time-consuming step in this routine is the computation of the session public key g^d′. But now d′ < r and, therefore, Algorithm 5.38 runs faster than Algorithm 5.36. One can easily check that forging a signature of Alice is computationally equivalent to determining Alice’s private key d from her public key g^d. The importance of using a new session key pair in each run of Algorithm 5.38 is exactly the same as in the case of ElGamal signatures.

The verification of Schnorr signatures (Algorithm 5.39) is based upon the fact that g^t = g^d′(g^d)^–s. Thus, the knowledge of g, s, t and g^d allows one to compute g^d′ and subsequently H(M ‖g^d′). The algorithm involves two exponentiations with both the exponents (t and s) being ≤ r. Thus, signature verification is also faster in the Schnorr scheme than in the ElGamal scheme.

Algorithm 5.39. Schnorr signature verification

Input: A signature (M, s, t) and the signer’s public key gd. Output: Verification status of the signature. Steps: u := gt(gd)s. . if { Return “Signature verified”. } else { Return “Signature not verified”. }

5.4.5. The Nyberg–Rueppel Digital Signature Algorithm

The Nyberg–Rueppel (NR) signature algorithm is another adaptation of the ElGamal signature scheme and is based on the intractability of solving the DLP in a group G. We assume that ord G = n has a large prime divisor r and that an element of order r is available. Here, a key pair is of the form (d, g^d), where the private key d is an integer between 2 and r – 1 (both inclusive) and where the public key g^d is an element of 〈g〉. The hash function H converts bit strings to elements of . We also assume the existence of a (publicly known) function .

NR signature generation can be performed as in Algorithm 5.40.

Algorithm 5.40. Nyberg–Rueppel signature generation

Input: A message M to be signed and the signer’s private key d. Output: The signature (M, s, t) on M. Steps: Generate a random session key pair (d′, gd′), 2 ≤ d′ ≤ r – 1. s := H(M) + F(gd′) (mod r). t := d′ – ds (mod r).

The only difference between NR signature generation and Schnorr signature generation is the way how s is computed. Therefore, whatever we remarked in connection with the security and the efficiency of the Schnorr scheme applies equally well to the NR scheme. Signature verification is also very analogous, as Algorithm 5.41 explains.

Algorithm 5.41. Nyberg–Rueppel signature verification

Input: A signature (M, s, t) and the signer’s public key gd. Output: Verification status of the signature. Steps: u := gt(gd)s. (mod r). if { Return “Signature verified”. } else { Return “Signature not verified”. }

5.4.6. The Digital Signature Algorithm (DSA)

The digital signature algorithm (DSA) has been proposed as a standard by the US National Institute of Standards and Technology (NIST) and later accepted as a Federal Information Processing Standard (FIPS) by the US government. This standard is also known as the digital signature standard (DSS). See the NIST document [220] for a complete description of this standard.

Algorithm 5.42. Generation of DSA primes

Input: An integer λ, 0 ≤ λ ≤ 8. Output: A prime p of bit length l := 512+64λ such that p – 1 has a prime divisor r of length 160 bits. Steps: Let l – 1 = 160n + b, 0 ≤ b < 160.     /* n = (l–1) quot 160, b = (l–1) rem 160. */ while (1) {    do {        Choose a random seed σ which is a bit string of length k ≥ 160.        Compute the bit string u := H(σ) ⊕ H((σ + 1) rem 2k).        r := u OR 2159 OR 1.    /* Set the most and least significant bits of u */    } while (r is not a prime).    i := 0, f := 2.    while (i < 4096) {        for j = 0, 1, . . . , n { vj := H((σ + f + j) rem 2k). }        v := v0 + v12160 + · · · + vn–12160(n–1) + (vn rem 2b)2160n + 2l–1.                                                      /* v is an integer of bit length exactly l */        p := v – (v rem 2r) + 1.   /* p – 1 is a multiple of 2r */        if (p is prime) { Return (p, r). }        i++, f := f + n + 1.    } }

DSA is based on the intractability of the DLP in the finite field , where p is a prime of bit length 512+64λ with 0 ≤ λ ≤ 8. The cardinality p–1 of is required to have a prime divisor r of length (exactly) 160 bits. The NIST document [220] specifies a standard method for obtaining such a field , which we describe in Algorithm 5.42. We denote by H the SHA-1 hash function that converts bit strings of arbitrary length to bit strings of length 160. We will identify (often without explicit mention) the bit string a₁a₂. . . a_k of length k with the integer a₁2^k–1 + a₂2^k–2 + · · · + a_k–12 + a_k.

The DSA prime generation procedure (Algorithm 5.42) starts by selecting the prime divisor r and then tries to find a prime p such that r|(p–1). The outputs of H are utilized as pseudorandomly generated bit strings of length 160.

Once the DSA parameters p and r are available, an element of multiplicative order r can be computed by Algorithm 3.26. Henceforth we assume that p, r and g are public knowledge and need not be supplied as inputs to the signature generation and verification routines. A DSA key pair consists of an integer (the private key) d, 2 ≤ d ≤ r – 1, and the element g^d (the public key) of .

The DSA signature-generation procedure is given as Algorithm 5.43. One may additionally include a check whether s = 0 or t = 0, and, if so, one should repeat signature generation with another session key. But this, being an extremely rare phenomenon, can be ignored for all practical purposes. Both s and t are elements of and hence are represented as integers between 0 and r – 1.

Algorithm 5.43. DSA signature generation

Input: A message M to be signed and the signer’s private key d. Output: The signature (M, s, t) on M. Steps: Generate a random session key d′, 2 ≤ d′ ≤ r – 1. t := d′–1(H(M) + ds) (mod r).

DSA signature verification is described in Algorithm 5.44. For a valid signature (M, s, t) on a message M, the algorithm computes w ≡ d′(H(M) + ds)^–1 (mod r), w₁ ≡ H(M)w (mod r) and w₂ ≡sw (mod r). Therefore, g^w₁ (g^d)^w₂ ≡ g^w₁+dw₂ ≡ g^w(H(M)+ds) ≡ g^{d′(H(M)+ds)–1 (H(M)+ds)} ≡ g^d′ (mod p). Reduction modulo r now gives .

Algorithm 5.44. DSA signature verification

Input: A signature (M, s, t) and the signer’s public key gd. Output: Verification status of the signature. Steps: if ( or ) { Return “Signature not verified”. } w := t–1 (mod r). w1 := H(M)w (mod r). w2 := sw (mod r). if { Return “Signature verified”. } else { Return “Signature not verified”. }

DSA signature generation performs a single exponentiation and DSA verification does two exponentiations modulo p. All the exponents are positive and ≤ r. Thus, DSA is essentially as fast as the Schnorr scheme or the NR scheme.

*5.4.7. The Elliptic Curve Digital Signature Algorithm (ECDSA)

The ECDSA is the elliptic curve analog of the DSA. Algorithm 5.45 describes the generation of the domain parameters necessary to set up an ECDSA system. One first selects a suitable finite field and takes a random elliptic curve E over . E must be such that the cardinality n of the group has a suitably large prime divisor r. One generates a random point of order r and works in the subgroup 〈P〉 of generated by P. It is assumed that q is either a prime p or a power 2^m of 2.

Algorithm 5.45. Generation of ECDSA parameters

Input: A finite field , where q is a prime p or a power 2m of 2. Output: A set of parameters E, n, r, P for the ECDSA. Steps: while (1) {   Choose a,  randomly.   Consider the curve .   Compute n := ord .   if (n has a prime divisor r > max(2160, )) {      if (n  (qk – 1) for k = 1, . . . , 20) and (n ≠ q) {         do {           Select  randomly.           P := (n/r)P′.         } while ().      }   } }

The order n = ord can be computed using the SEA algorithm (for q = p) or the Satoh–FGH algorithm (for q = 2^m) described in Section 3.6. The integer n should be factored to check if it has a prime divisor r > max(2¹⁶⁰, ). The condition n  (q^k – 1) for small values of k is necessary to avoid the MOV attack, whereas the condition n ≠ q ensures that the SmartASS attack cannot be mounted. is not necessarily a cyclic group. But, r being a prime, a point must be one of order r.

An ECDSA key pair consists of a private key d (an integer in the range 2 ≤ d ≤ r – 1) and the corresponding public key . H denotes the hash function SHA-1 that converts bit strings of arbitrary length to bit strings of length 160. As discussed in connection with DSA, we identify bit strings with integers. We also make an association of elements of with integers in the set {0, 1, . . . , q – 1}. ECDSA signatures can be generated as in Algorithm 5.46. It is necessary to check the conditions s ≠ 0 and t ≠ 0. If these conditions are not both satisfied, one should re-run the procedure with a new session key pair.

Algorithm 5.46. ECDSA signature generation

Input: A message M to be signed and the signer’s private key d. Output: The signature (M, s, t) on M. Steps: Generate a random session key pair (d′, d′P), 2 ≤ d′ ≤ r – 1. /* Let us denote */ s := h (mod r). t := d′–1 (H(M) + ds) (mod r).

ECDSA signature verification is explained in Algorithm 5.47. The correctness of this algorithm can be proved like that of Algorithm 5.44.

Algorithm 5.47. ECDSA signature verification

Input: A signature (M, s, t) and the signer’s public key dP. Output: Verification status of the signature. Steps: if ( or ) { Return “Signature not verified”. } w := t–1 (mod r). w1 := H(M)w (mod r). w2 := sw (mod r). Q := w1P + w2(dP). if () { Return “Signature not verified”. } /* Otherwise denote */ (mod r). if { Return “Signature verified”. } else { Return “Signature not verified”. }

*5.4.8. The XTR Signature Algorithm

As discussed in Section 5.2.7, the XTR family of algorithms is an adaptation of other conventional algorithms over finite fields. XTR achieves a speed-up of about three using a clever way of representing elements in certain finite fields. It is no surprise that the DLP-based signature algorithms, described so far, can be given efficient XTR renderings. We explain here XTR–DSA, the XTR version of the digital signature algorithm.

In order to set up an XTR system, we need a prime p ≡ 2 (mod 3). The XTR group G is a subgroup of the multiplicative group and has a prime order q dividing p² – p + 1. For compliance with the original version of DSA, one requires q to be of bit length 160. The trace map taking is used to represent an element by the element . Under this representation, arithmetic in G translates to that in . For example, we have seen how exponentiation in G can be efficiently implemented using arithmetic (Algorithm 5.20). The trace Tr(g) of a generator g of G should also be made available for setting up the XTR domain parameters. In Section 5.2.7, we have discussed how a random set of XTR parameters (p, q, Tr(g)) can be computed.

An XTR key comprises a random integer (the private key) and the trace (the public key). Algorithm 5.20 is used to compute Tr(g^d) from Tr(g) and d. This algorithm gives Tr(g^d–1) and Tr(g^d+1) as by-products. For an implementation of XTR–DSA, we require these two elements of . So we assume that the public key consists of the three traces S_d(Tr(g)) = (Tr(g^d–1), Tr(g^d), . As explained in Lenstra and Verheul [172], the values Tr(g^d–1) and Tr(g^d+1) can be computed easily from Tr(g^d) even when d is unknown, so it suffices to store only Tr(g^d) as the public key. But we avoid the details of this computation here and assume that all the three traces are available to the signature verifier.

Algorithm 5.20 provides an efficient way of computing exponentiations in G. For DSA-like signature verification (cf. Algorithm 5.44), one computes products of the form g^a(g^d)^b with d unknown. In the XTR world, this amounts to computing the trace Tr(g^a(g^d)^b) from the knowledge of a, b, Tr(g) and Tr(g^d) (or S_d(Tr(g))) but without the knowledge of d. The XTR exponentiation algorithm is as such not applicable in such a situation. We should, therefore, prescribe a method to compute traces of products in G. Doing that requires some mathematics that we mention now without proofs. See Lenstra and Verheul [170] for the missing details.

Let e :=ab^–1 (mod q). Then, a + bd ≡b(e + d) (mod q), that is, Tr(g^a(g^d)^b) = Tr(g^b(e+d)), that is, it is sufficient to compute Tr(g^e+d) from the knowledge of e, Tr(g) and Tr(g^d). We treat the 3-tuple S_k(Tr(g)) as a row vector (over ). For , let M_c denote the matrix

Equation 5.9

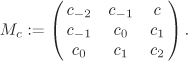
We take c := Tr(g). It can be shown that det , that is, the matrix M_Tr(g) is invertible, and we have:

Equation 5.10

Here the superscript ^t denotes the transpose of a matrix. With these observations, one can write the procedure for computing Tr(g^a(g^d)^b) as in Algorithm 5.48.

Algorithm 5.48. XTR multiplication

Input: a, b, Tr(g) and Sd(Tr(g)) for some unknown d. Output: Tr(ga(gd)b). Steps: Compute e := ab–1 (mod q). Compute Se(Tr(g)) using Algorithm 5.20 with c := Tr(g) and n := e. Use Equation (5.10) to compute Tr(ge+d). Use Algorithm 5.20 with c := Tr(ge+d) and n := b to compute     . Return Tr(gb(e+d)).

XTR–DSA signature generation (Algorithm 5.49) is an obvious adaptation of Algorithm 5.43.

Algorithm 5.49. XTR signature generation

Input: A message M to be signed and the signer’s private key d. Output: The signature (M, s, t) on M with s, . Steps: do {   Generate a random .   Compute Tr(gd′).          /* Use Algorithm 5.20 with c := Tr(g) and n := d′ */   Let Tr(gd′) = x1α + x2α2.     /* α is defined in Section 5.2.7 to represent  */   s := x1 + px2 (mod q). } while (s ≠ 0). t := d′–1(H(M) + ds) (mod q).         /* Here H is the hash function SHA-1 */

The bulk of the time taken by Algorithm 5.43 goes for the computation of Tr(g^d′). Since the trace representation of XTR makes this exponentiation three times as efficient as the corresponding DSA exponentiation, XTR–DSA signature generation runs nearly three times as fast as DSA signature generation.

XTR–DSA signature verification can be easily translated from Algorithm 5.44 and is shown in Algorithm 5.50. The most costly step in the XTR–DSA verification routine is the computation of Tr(g^w₁ (g^d)^w₂). One uses Algorithm 5.48 for this purpose. This algorithm, in turn, invokes the exponentiation Algorithm 5.20 twice. For the original DSA signature verification (Algorithm 5.44), the costliest step is the computation of g^w₁ (g^d)^w₂, which involves two exponentiations and a (cheap) multiplication. A careful analysis shows that XTR–DSA signature verification runs nearly 1.75 times faster than DSA verification.

Algorithm 5.50. XTR signature verification

Input: XTR–DSA signature (M, s, t) on a message M and the signer’s public key (Tr(gd–1), Tr(gd), Tr(gd+1)). Output: Verification status of the signature. Steps: if or { Return “Signature not verified”. } w := t–1 (mod q). w1 := H(M)w (mod q). w2 := sw (mod q). Compute Tr(gw1 (gd)w2). /* Use Algorithm 5.48 */ Write this trace value as . /* See Section 5.2.7 */ (mod q). if { Return “Signature verified”. } else { Return “Signature not verified”. }

*5.4.9. The NTRUSign Algorithm

The NTRU Signature Scheme (NSS) (Hoffstein et al. [131]) is an adaptation of the NTRU encryption algorithm discussed in Section 5.2.8. Cryptanalytic studies (Gentry et al. [110]) show that the NSS has security flaws. A newer version of the NSS, referred to as NTRUSign and resistant to these attacks, has been proposed by Hoffstein et al. [128]. In this section, we provide a brief overview of NTRUSign.

In order to set up the domain parameters for NTRUSign, we start with an and consider the ring . Elements of R are polynomials with integer coefficients and of degrees ≤ n – 1. The multiplication of R is denoted by ⊛, which is essentially the multiplication of two polynomials of followed by setting Xⁿ = 1. We also fix a positive integer β to be used as a modulus for the coefficients of the polynomials in R. The subsets and of R are of importance for the NTRUSign algorithm, where for one defines , and where ν_f and ν_g are suitably chosen parameters. The message space is assumed to consist of pairs of polynomials of R with coefficients reduced modulo β. We further assume that we have at our disposal a hash function H that maps messages (that is, binary strings) to elements of .

Let . The average of the coefficients of a is denoted by . The centred norm ‖a‖ of a is defined by

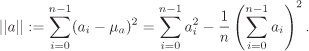
For two polynomials a, , one also defines

‖(a, b)‖² := ‖a‖² + ‖b‖².

The parameters ν_f and ν_g should be so chosen that any polynomial and any polynomial have (centred) norms on the order O(n). An upper bound B on the norms (of pairs of polynomials) should also be predetermined.

Typical values for NTRUSign parameters are

(n, β, ν_f, ν_g, B) = (251, 128, 73, 71, 300).

It is estimated that these choices lead to a security level at least as high as in an RSA scheme with a 1024-bit modulus. For very long-term security, one may go for (n, β) = (503, 256).

In order to set up a key pair, the signer first chooses two random polynomials and . The polynomial f should be invertible modulo β and the signer computes with the property that f_β ⊛ f ≡ 1 (mod β). The public key of the signer is the polynomial h ≡ f_β ⊛ g (mod β), whereas the private key is the tuple (f, g, F, G), where F and G are two polynomials in R satisfying

f ⊛ G – g ⊛ F = q

and

‖F‖, ‖G‖ = O(n).

Hoffstein et al. [128] present an algorithm to compute F and G with ‖F‖, from polynomials f and g with ‖f‖, , where c is a given constant.

Algorithm 5.51. NTRU signature generation

Input: A message M to be signed and the signer’s private key (f, g, F, G). Output: The signature (M, s) on M. Steps: Compute . Compute polynomials A, B, a, satisfying G ⊛ m1 – F ⊛ m2 = A + βB, –g ⊛ m1 + f ⊛ m2 = a + βb, where a and A have coefficients in the range between –β/2 and +β/2. Compute s ≡ f ⊛ B + F ⊛ b (mod β).

NTRUSign signature generation is described in Algorithm 5.51. It is apparent that the NTRUSign algorithm derives its security from the difficulty in computing a vector v in a certain lattice, close to the vector defined by the hashed message (m₁, m₂). For defining the lattice, we first note that a polynomial can be identified as a vector (u₀, u₁, . . . , u_n–1) of dimension n defined by its coefficients. Similarly, two polynomials u, define a vector, denoted by (u, v), of dimension 2n. To the public key h we associate the 2n-dimensional lattice

It is clear from the definitions that both (f, g) and (F, G) are in L_h.

If h = (h₀, h₁, . . . , h_n–1), then for each i = 0, 1, . . . , n – 1 we have

Xi ⊛ h(X)	≡	(hn–i, . . . , hn–1, h0, . . . , hn–i–1) (mod β) and
0 ⊛ h(X)	≡	βXi (mod β).

It follows immediately that L_h is generated by the rows of the matrix

Now, consider the signature generation routine (Algorithm 5.51). The hash function H generates from the message M a random 2n-dimensional vector m := (m₁, m₂) not necessarily on L_h. We then look at the vector v := (s, t) defined as:

s	≡	f ⊛ B + F ⊛ b (mod β), and
t	≡	g ⊛ B + G ⊛ b (mod β).

The lattice L_h has the rotational invariance property, namely, if , then (Xⁱ ⊛ u, Xⁱ ⊛ v) is also in L_h for all i = 0, 1, . . . , n – 1. More generally, if , then for any polynomial . In particular, since v = (s, t) = B ⊛ (f, g) + b ⊛ (F, G) (mod β) and since (f, g), , it follows that . Of these two polynomials only s is needed for the generation of NTRUSign signatures. The other is needed during signature verification and can be computed easily from s using the formula t ≡ h ⊛ s (mod β), the validity of which is established from the definition of the lattice L_h.

The vector is close to the message vector m in the sense that

for the constant c chosen earlier (see Hoffstein et al. [128] for a proof of this relation). The verification routine can, therefore, be designed as in Algorithm 5.52.

Algorithm 5.52. NTRU signature verification

Input: A signature (M, s) and the signer’s public key h. Output: Verification status of the signature. Steps: Compute . Compute t ≡ h ⊛ s (mod β). if (‖(m1 – s, m2 – t)‖ ≤ B) { Return “Signature verified”. } else { Return “Signature not verified”. }

For the choice (n, β, c) = (251, 128, 0.45), we have ‖(m₁ – s, m₂ – t)‖ ≈ 216. Therefore, choosing the norm bound B slightly larger than this value (say, B = 300) allows the verification scheme to work correctly most of the time. The knowledge of the private key (f, g, F, G) allows the legitimate signer to compute the close vector (s, t) easily. On the other hand, for a forger (who is lacking the private information) fast computation of a vector v′ = (s′, t′) with small norm ‖(m₁ – s′, m₂ – t′)‖ (say ≤ 400 for the above parameter values) seems to be an intractable task. This is precisely why forging an NTRUSign signature is considered infeasible.

An exhaustive search can be mounted for generating a valid signature (s′, t′) on a message M with H(M) = (m₁, m₂). More precisely, a forger fixes half of the 2n coefficients of the polynomials s′ and t′ and then tries to solve t′ ≡ h ⊛ s′ (mod β) for the remaining half such that the norm ‖(m₁ – s′, m₂ – t′)‖ is small. It is estimated (see Hoffstein et al. [128] for the details) that the probability that a random guess for the unknown half succeeds is very low (≤ 2^–178.44 for the given parameter values).

Another attack on the NTRUSign scheme is to determine the polynomials f, g from a knowledge of h. Since (f, g) is a short non-zero vector in the lattice L_h, an algorithm that can find such vectors can determine (f, g) (or a rotated version of it). However, for a proper choice of the parameters such an algorithm is deemed infeasible. (Also see the NTRU encryption scheme in Section 5.2.8.)

Similar to the NTRU encryption scheme, the NTRUSign scheme is fast, namely, both signature generation and verification can be carried out in time O(n²). This is one of the main reasons why the NTRUSign scheme deserves popularity. Indeed, it may be adopted as an IEEE standard. Unfortunately, however, several attacks on NTRUSign are known. Gentry and Szydlo [111] indicate the possibility of extending the attacks of Gentry et al. [110]. Nguyen [217] proposes a more concrete attack on NTRUSign, that is capable of recovering the private key from only 400 signatures. The future of NTRUSign and its modifications remains uncertain.

5.4.10. Blind Signature Schemes

Suppose that an entity (Alice) referred to as the sender or the user, wants to get a message M signed by a second entity (Bob) called the signer, without revealing M to Bob. This can be achieved as follows. First Alice transforms the message M to and sends to Bob. Bob generates the signature (, σ) on and sends this pair back to Alice. Finally, Alice applies a second transform g to generate the signature of Bob on M. The transform f hides the actual message M from Bob and, thereby, disallows Bob from associating Alice with the signed message (M, s). Such a signature scheme is called a blind signature scheme.

Blind signatures are widely used in electronic payment systems in which Alice (a customer) wants the signature of Bob (the bank) on an electronic coin, but does not want the bank to be capable of associating Alice with the coin. In this way, Alice achieves anonymity while spending an electronic coin.

In a blind signature scheme, Bob does not know M, but his signature on is essential for Alice to reconstruct the signature on M. Furthermore, the blind signature on M should not allow Alice to compute the blind signature on another message M′. More generally, Alice should not be able to generate l + 1 (or more) blind signatures with only l (or fewer) interactions with Bob. A forgery of this kind is often called an (l, l + 1) forgery or a one-more forgery (in case l is bounded above by a polynomial in the security parameter) or a strong one-more forgery (in case l is bounded above poly-logarithmically in the security parameter). An (l, l + 1) forgery is mountable on a scheme which is not existentially unforgeable (Exercises 5.15 and 5.19). Usually, existential forgery gives forged signatures on messages over which the forger has no (or little) control (that is, on messages which are likely to be meaningless).

Now, we describe some common blind signature schemes. We provide a brief overview of the algorithms. Detailed analysis of the security of these schemes can be found in the references cited at the end of this chapter.

Chaum’s RSA blind signature protocol

Chaum’s blind signature protocol is based on the intractability of the RSAP (or the IFP). The signer generates two (distinct) large random primes p and q and computes n := pq. He then chooses a random integer e with gcd(e, φ(n)) = 1 and computes an integer d such that ed ≡ 1 (mod φ(n)). The public key (of the signer) is the pair (n, e), whereas the private key is d. Chaum’s protocol works as in Algorithm 5.53.

Algorithm 5.53. Chaum’s RSA blind signature

Input: A message M generated by Alice. Output: Bob’s blind RSA signature (M, s) on M. Steps: Alice hashes the message M to . Alice chooses a random and computes . Alice sends to Bob. Bob generates the signature on . Bob sends σ to Alice. Alice computes Bob’s (blind) signature s := ρ–1σ (mod n) on M.

Since σ ≡ (ρ^em)^d ≡ρm^d (mod n), we have s ≡ρ^–1σ ≡ m^d (mod n), that is, s is indeed the RSA signature of Bob on M. Bob receives and gains no idea about m, since ρ is randomly and secretly chosen by Alice.

The Schnorr blind signature protocol

Let G be a finite multiplicative Abelian group and let be of order r (a large prime). We assume that computing discrete logarithms in G is an infeasible task. The key pair of the signer is denoted by (d, g^d), where the integer d, 2 ≤ d ≤ r – 1, is the private key and g^d the public key. The Schnorr blind signature protocol is described in Algorithm 5.54.

Algorithm 5.54. Schnorr blind signature

Input: A message M generated by Alice. Output: Bob’s blind Schnorr signature (M, s, t) on M. Steps: Alice asks Bob to initiate a communication. Bob chooses a random and computes . Bob sends to Alice. Alice selects α, randomly. Alice computes . Alice computes and . Alice sends to Bob. Bob computes . Bob sends to Alice. Alice computes .

It is easy to check that the output (M, s, t) of Algorithm 5.54 is a valid Schnorr signature of Bob on the message M. The session key d′ (Algorithm 5.38) for this signature is . Since d and are secret knowledges of Bob, Alice must depend on Bob for the computation of . The message M is never sent to Bob. Also its hash is masked by β. This is how this protocol achieves blindness.

The Okamoto–Schnorr blind signature protocol

Okamoto’s adaptation of the Schnorr scheme is proved to be resistant to an attack by a third entity (Pointcheval and Stern [237]). As in the Schnorr scheme, we fix a (finite multiplicative Abelian) group G (in which it is difficult to compute discrete logarithms). We then choose two elements g₁, of (large prime) order r. The private key of the signer now comprises a pair (d₁, d₂) of integers in {2, . . . , r – 1}, whereas the public key y is the group element . We assume that there is a hash function H whose outputs are in . We identify elements of G as bit strings. The Okamoto–Schnorr blind signature protocol is explained in Algorithm 5.55.

Algorithm 5.55. Okamoto–Schnorr blind signature

Input: A message M generated by Alice. Output: Bob’s blind signature (M, s1, s2, s3) on M. Steps: Alice asks Bob to initiate a communication. Bob chooses random and computes . Bob sends to Alice. Alice selects α, β, randomly. Alice computes . Alice computes and . Alice sends to Bob. Bob computes and . Bob sends and to Alice. Alice computes and .

An Okamoto–Schnorr signature (M, s₁, s₂, s₃) on a message can be verified by checking the equality s₁ = H(M‖u), where . Each invocation of the protocol uses a session private key . Alice must depend on Bob for generating s₂ and s₃, because she is unaware of the private values d₁, d₂, and . Alice, in an attempt to forge Bob’s blind signature, may start with random and of her choice. But she still needs the integers d₁ and d₂ in order to complete the protocol. The blindness of Algorithm 5.55 stems from the fact that the message M is never sent to Bob and its hash is masked by γ.

5.4.11. Undeniable Signature Schemes

So far we have seen signature schemes for which any entity with a knowledge of the signer’s public key can verify the authenticity of a signature. There are, however, situations where an active participation of the signer is necessary for the verification of a signature. Moreover, during a verification interaction a signer should not be allowed to deny a legitimate signature made by him. A signature meeting these requirements is called an undeniable signature.

Undeniable signatures are typically used for messages that are too confidential or private to be given unlimited verification facility. In case of a dispute, an entity should be capable of proving a forged signature to be so and at the same time must accept the binding to his own valid signatures. So in addition to the signature generation and verification protocols, an undeniable signature scheme comes with a denial or disavowal protocol to guard against a cheating signer that is unwilling to accept his valid signature either by not taking part in the verification interaction or by responding incorrectly or by claiming a valid signature to be forged.

There are applications where undeniable signatures are useful. For example, a software vendor can use undeniable signatures to prove the authenticity of its products only to its (paying) customers (and not to everybody).

Chaum and van Antwerpen gave a first concrete realization of an undeniable signature scheme [52, 51]. It is based on the intractability of computing discrete logs in the group , p a prime. Gennaro et al. [109] later adapted the algorithm to design an RSA-based undeniable signature scheme. We now describe these two schemes. Rigorous studies of these schemes can be found in the original papers. See also [53, 186, 187, 102, 202, 230].

The Chaum–Van Antwerpen undeniable signature scheme

For setting up the domain parameters for Chaum–Van Antwerpen (CvA) signatures, Bob chooses a (large) prime p of the form p = 2r + 1, where r is also a prime. (Such a prime p is called a safe prime (Definition 3.5).) Bob finds a random element of multiplicative order r, selects a random integer and computes y := g^d (mod p). Bob publishes (p, g, y) as his public key and keeps the integer d secret as his private key. The value d^–1 (mod r) is needed during verification and can be precomputed and stored (secretly) along with d. We assume that we have a hash function H that maps messages (that is, bit strings) to elements of the subgroup of order r in . In order to generate a CvA signature on a message M, Bob carries out the steps given in Algorithm 5.56. Verification of Bob’s CvA signature by Alice involves the interaction given in Algorithm 5.57.

Algorithm 5.56. Chaum–Van Antwerpen undeniable signature generation

Input: The message M to be signed and the signer’s private key (p, d). Output: The signature (M, s) on M. Steps: m := H(M). s := md (mod p).

If (M, s) is a valid CvA signature, then

v ≡ (sⁱy^j)^{d–1 (mod r)} ≡ ((m^d)ⁱ(g^d)^j)^{d–1 (mod r)} ≡ mⁱg^j ≡ v′ (mod p).

On the other hand, if s ≢ m^d (mod p), Bob can guess the element v′ with a probability of only 1/r, even under the assumption that Bob has unbounded computing resources. This means that unless the signature (M, s) is valid, it is extremely unlikely that Bob can make Alice accept the signature.

The denial protocol for the CvA scheme involves an interaction between the prover Bob and the verifier Alice, as given in Algorithm 5.58. In order to see how this denial protocol works, we note that Algorithm 5.58 essentially makes two calls of the verification protocol. First assume that Bob executes the protocol honestly, that is, Bob follows the steps as indicated. If the signature (M, s) is a valid one, the check v₁ ≡ m^i₁ g^j₁ (mod p) (as well as the check v₂ ≡ m^i₂ g^j₂ (mod p)) should succeed and Alice’s decision to accept the signature as valid is justified. On the other hand, if (M, s) is a forged signature, that is, if s ≢ m^d (mod p), then the probability that each of these checks succeeds is 1/r as discussed before. Thus, it is extremely unlikely that a forged signature is accepted as valid by Alice. So Alice eventually computes both w₁ and w₂ equal to s^{i₁ i₂d–1 (mod r)} (mod p) and accepts the signature to be forged. Finally, suppose that Bob is intending to deny the (purported) signature (M, s). If Bob does not fully take part in the interaction, then his intention becomes clear. Otherwise, he sends v₁ and/or v₂ not computed according to the formulas specified. In that case, Bob succeeds in making Alice compute w₁ = w₂ with a probability of only 1/r. Thus, it is extremely unlikely that Bob executing this protocol dishonestly can successfully disavow a valid signature.

Algorithm 5.57. Chaum–Van Antwerpen undeniable signature verification

Input: A CvA signature (M, s) on a message M. Output: Verification status of the signature. Steps: Alice computes m := H(M). Alice chooses two secret random integers i, . Alice computes u := siyj (mod p). Alice sends u to Bob. Bob computes v := ud–1 (mod r) (mod p). Bob sends v to Alice. Alice computes v′ := migj (mod p). Alice accepts the signature (M, s) if and only if v = v′.

Algorithm 5.58. Chaum–Van Antwerpen undeniable signature: denial protocol

Input: A (purported) CvA signature (M, s) of Bob on a message M. Output: One of the following decisions by Alice: The signature is valid. The signature is forged. Bob is trying to deny the signature. Steps: Alice computes m := H(M). Alice chooses two secret random integers i1, . Alice computes u1 := si1 yj1 (mod p) and sends u1 to Bob. Bob computes (mod p) and sends v1 to Alice. if (v1 ≡ mi1 gj1 (mod p)) {    Alice accepts the signature (M, s) to be valid and quits the protocol. } Alice chooses two other secret random integers i2, . Alice computes u2 := si2 yj2 (mod p) and sends u2 to Bob. Bob computes and sends v2 to Alice. if (v2 ≡ mi2 gj2 (mod p)) {    Alice concludes the signature (M, s) to be valid and quits the protocol. } Alice computes w1 := (v1g–j1)i2 (mod p) and w2 := (v2g–j2)i1 (mod p). if (w1 = w2) {    Alice concludes that the signature is forged. } else {    Alice concludes that Bob is trying to deny the signature. }

RSA-based undeniable signature scheme

Gennaro, Krawczyk and Rabin’s undeniable signature scheme (the GKR scheme) is based on the (intractability of the) RSA problem.

A GKR key pair differs from a usual RSA key pair. The signer chooses two (large) random primes p and q such that both p′ := (p – 1)/2 and q′ := (q – 1)/2 are also prime, and sets n := pq. Two integers e and d satisfying ed ≡ 1 (mod φ(n)) are then selected. Finally, one requires a , g ≠ 1, and y ≡ g^d (mod n). The public key of the signer is the tuple (n, g, y), whereas the private key is the pair (e, d). It can be shown that g need not be a random element of . Choosing a (fixed) small value of g (for example, g = 2) does not affect the security of the GKR protocol, but makes certain operations (computing powers of g) efficient.

Algorithm 5.59. GKR RSA undeniable signature generation

Input: The message M to be signed and the signer’s private key (e, d). Output: The signature (M, s) on M. Steps: m := H(M). /* Hash the message M to an element m of */ s := md (mod n).

GKR signature generation (Algorithm 5.59) is the same as in RSA. The verification protocol described in Algorithm 5.60 accepts, in addition to a valid GKR signature (M, s), the signatures (M, αs), where has multiplicative order 1 or 2 (there are four such values of α). In view of this, we define the subset

of . Any element is considered to be a valid signature on M. Since Bob knows p and q, he can easily find out all the elements α of of order ≤ 2 and can choose to output (M, αH(M)^d) as the GKR signature for any such α. Taking α = 1 (as in Algorithm 5.59) is the canonical choice, but during the execution of the denial protocol Bob will not be allowed to disavow other valid choices.

The interaction between the prover Bob and the verifier Alice during GKR signature verification is given in Algorithm 5.60. It is easy to see that if (M, s) is a valid GKR signature, then v = v′. On the other hand, if (M, s) is a forged signature, that is, if s ∉ Sig M, then the equality v = v′ occurs with a probability of , even in the case that the forger has unbounded computational resources.

Algorithm 5.60. GKR RSA undeniable signature verification

Input: A GKR signature (M, s) on a message M. Output: Verification status of the signature. Steps: Alice computes m := H(M). Alice chooses random i, . Alice computes u := s2iyj (mod n). Alice sends u to Bob. Bob computes v := ue (mod n). Bob sends v to Alice. Alice computes v′ := m2igj (mod n). Alice accepts the signature (M, s) if and only if v = v′.

Algorithm 5.61. GKR RSA undeniable signature: denial protocol

Input: A (purported) GKR signature (M, s) of Bob on a message M. Output: One of the following decisions by Alice: The signature is forged. Bob is trying to deny the signature. Steps: Alice computes m := H(M). Alice chooses random and . Alice computes w1 := migj (mod n) and w2 := siyj (mod n). Alice sends (w1, w2) to Bob. Bob computes m := H(M). Bob determines such that the following congruence holds: Equation 5.11 if (no such i′ is found) {    /* This may happen, if Alice has cheated */    Bob aborts the protocol. } Bob sends i′ to Alice. if (i = i′) {    Alice concludes that the signature is forged. } else {    Alice concludes that Bob is trying to deny the signature. }

The denial protocol for the GKR scheme is described in Algorithm 5.61. This protocol is executed, after verification by Algorithm 5.60 fails. In that case, Alice wants to ascertain whether the signature is actually invalid or Bob has denied his valid signature by incorrectly executing the verification protocol. A small integer k is predetermined for the denial protocol. The prover needs a running time proportional to k, whereas the probability of a successful denial of a valid signature decreases with k. Taking k = O(lg n) gives optimal performance.

In order to see how this protocol prevents Bob from denying a valid signature, first consider the case that (M, s) is a valid GKR signature of Bob. In that case, . On the other hand, s^e ≡ α^em^de ≡ α^em (mod n). Therefore, for every , one has . Thus, Bob can only guess the secret value of i chosen by Alice and the guess is correct with a probability of 1/k. On the other hand, if (M, s) is a forged signature, Congruence (5.11) holds only for a single i′, that is, for i′ = i (Exercise 5.23). Sending i′ will then convince Alice that the signature is really forged. In both these cases, Congruence (5.11) holds for at least one i′. Failure to detect such an i′ implies that the value(s) of w₁ and/or w₂ have not been correctly sent by Alice. The protocol should then be aborted.

In order to reduce the probability of successful cheating, it is convenient to repeat the protocol few times instead of increasing k. If k = 1024, Bob can successfully cheat in eight executions of the denial protocol with a probability of only 2^–80.

5.4.12. Signcryption

The conventional way to ensure both authentication and confidentiality of a message is to sign the message first and then encrypt the signed message. Now that we have many signature and encryption algorithms in our bag, there is hardly any problem in achieving both the goals simultaneously. Zheng proposes signcryption schemes that combine these two operations together. A signcryption scheme is better than a sign-and-encrypt scheme in two aspects. First, the combined primitive takes less running time than the composite primitive comprising signature generation followed by encryption. Second, a signcrypted message is of smaller size than a signed-and-encrypted message. When communication overheads need to be minimized, signcryption proves to be useful.

Before describing the signcryption primitive, let us first review the composite sign-and-encrypt scheme. Let M be the message to be sent. Alice the sender generates the signature appendix s on M using one of the signature schemes described earlier. This step can be described as s = f_s(M, d_a), where d_a is the private key of Alice. Next a symmetric key k is generated by Alice. The message M is encrypted by a symmetric cipher (like DES) under the key k, that is, C := E(M, k). The key k is then encrypted using an asymmetric routine under the public-key e_b of Bob the recipient, that is, c = f_e(k, e_b). The triple (C, c, s) is then transmitted to Bob.

Upon reception of (C, c, s) Bob first retrieves k using his private key d_b, that is, k = f_d(c, d_b). The message M is then recovered by symmetric decryption: M = D(C, k). Finally, the authenticity of M is verified from the signature using the verification operation: f_v(M, s, e_a), where e_a is the public key of Alice. Algorithm 5.62 describes the sign-and-encrypt operation and its inverse.

Algorithm 5.62. Sign-and-encrypt

s := fs(M, da). Generate a random symmetric key k. c := fe(k, eb). C := E(M, k). Send (C, c, s) to the recipient. Decrypt-and-verify k := fd(c, db). M := D(C, k). Verify the signature: fv(M, s, ea).

Zheng’s signcryption scheme combines f_s and f_e to a single operation f_se and also f_d and f_v to another single operation f_dv. Each of these combined operations essentially takes the time of a single public- or private-key operation and hence leads to a performance enhancement by a factor of nearly two. Moreover, the encrypted key c need not be sent with the message, that is, C and s are sufficient for both authentication and confidentiality. This reduces communication overhead.

Signcryption is based on shortened digital signature schemes. Table 5.3 describes the shortened version of DSA (Section 5.4.6). We use the notations of Algorithms 5.43 and 5.44. Also ‖ denotes concatenation of strings, and H is a hash function (like SHA-1). The shortened schemes have two advantages over the original DSA. First, a DSA signature is of length 2|r|, whereas an SDSA1 or SDSA2 signature has length |r| + |H(·)|. For the current version of the standard, both r and H(·) are of size 160 bits. However, one may use potentially bigger r and in that case the shortened schemes give smaller signatures with equivalent security. Finally, DSA requires computing a modular inverse during verification, whereas SDSA does not. So verification is more efficient in the shortened schemes.

Table 5.3. Shortened digital signature algorithms

Name	Signature generation	Signature verification
SDSA1	s := H(gd′ (mod p)‖M). t := d′(s + d)–1 (mod r).	w := (eags)t (mod p). Verify if s = H(w‖M).
SDSA2	s := H(gd′ (mod p)‖M). t := d′(1 + ds)–1 (mod r).	. Verify if s = H(w‖M).

Algorithms 5.63 and 5.64 provide the details of the signcryption algorithm and its inverse called unsigncryption. The algorithms use a keyed hash function KH. One may implement KH(x, ) as using an unkeyed hash function H.

Signcryption differs from the shortened scheme in that is used instead of g^d′ for the computation of s. The running time of the signcryption algorithm is dominated by this modular exponentiation. When signature and encryption are used separately, the encryption operation uses one (or more) exponentiations. So signcryption significantly improves upon the sign-and-encrypt scheme of Algorithm 5.62.

Algorithm 5.63. Signcryption

Input: Plaintext message M, the sender’s private key da, the recipient’s public key eb = gdb (mod p). Output: The signcrypted message (C, s, t). Steps: Select a random . .                /* Generate keys for both signing and encrypting. */ Write k := k1 ‖ k2 with |k2| equal to the length of a symmetric key. s := KH(M‖N, k1).                  /* Here N is the public key or the public key certificate of the sender. */ C := E(M, k2).                                                          /* Symmetric encryption */

Algorithm 5.64. Unsigncryption

Input: The signcrypted message (C, s, t), the sender’s public key ea = gda (mod p) and the recipient’s private key db. Output: The plaintext message M and the verification status of the signature. Steps: Write k := k1 ‖ k2 with |k2| equal to the length of a symmetric key. M := D(C, k2). /* Symmetric decryption */ if (KH(M‖N, k1) = s) { Return “Signature verified”. } else { Return “Signature not verified”. }

The most time-consuming part of unsigncryption is the computation of two modular exponentiations. DSA verification too has this property. However, an additional decryption in the decrypt-and-verify scheme of Algorithm 5.62 calls for one (or more) exponetiations, making it slower that unsigncryption.

Exercise Set 5.4

5.15	Show how first pre-image resistance of the hash function H plays an important role for RSA signatures (with appendix) described in Section 5.4.1. More precisely, show that if it is easy to find a pre-image of any hash value, it is easy to generate a valid signature (M, s) from two valid signatures (M1, s1) and (M2, s2) with M ∉ {M1, M2}. This is often referred to as existential forgery of a signature. [H] Describe how existential forgery is possible for the Rabin signature scheme. [H] Describe how existential forgery is possible for the ElGamal signature scheme. [H]
5.16	Assume that Bob uses the same RSA key pair ((n, e), d) for receiving encrypted messages and for signing. Suppose that Carol intercepts the ciphertext c ≡ me (mod n) sent by Alice. Also suppose that Bob is willing to sign any random message presented by Carol. Explain how Carol can choose a message to be signed by Bob in order to retrieve the secret m. [H]
5.17	Let G be a finite cyclic group of order n, and g a generator of G. Suppose that Alice’s private and public keys are respectively d and gd. Consider a variant of the ElGamal signature scheme, in which s is computed as in Algorithm 5.36, but the roles of d and d′ are interchanged in the generation of t, that is, the modified signature (s, ) on M is generated as: s := gd′, := d–1[H(M) – d′H(s)] (mod n). Write the verification routine for the modified scheme. Show that forging modified ElGamal signatures is as difficult as computing discrete logarithms in G. You may assume that a forger can arrange d′ of her choice. Explain why signature generation is (a bit) more efficient in the modified scheme. Suppose that because of this enhanced performance Alice decided to switch to the modified scheme, but for backward compatibility she maintained both the original signature (s, t) and the modified signature (s, ) on a message M. What went wrong?
5.18	Show that: There are two valid ECDSA signatures on each message. There are three valid XTR–DSA signatures on each message. (Here we call a signature valid, if it passes the verification routine.)
5.19	Write the versions with message recovery of the RSA, Rabin, Schnorr and Nyberg–Rueppel signature schemes. Describe the possibilities of existential forgery for these versions. (Since hash functions cannot be inverted, they are not used for signature schemes with message recovery, and so the problem of existential forgery is more acute in this case. To avoid such forgeries the signer should add some redundancy to each message block before signing the same. An existentially forged signature is likely to correspond to a message not containing the redundancy.)
5.20	Design the XTR version of the Nyberg–Rueppel signature scheme with appendix (Section 5.4.5). What are the speed-ups achieved by the signature generation and verification routines of the XTR version over the original NR routines?
5.21	Repeat Exercise 5.20 with the Schnorr digital signature scheme (Section 5.4.4).
5.22	Deduce that the determinant of the matrix Mc of Equation (5.9) is Demonstrate that [View full size image]
5.23	Let p, q, p′, q′ be distinct odd primes with p = 2p′ + 1 and q = 2q′ + 1, and let n := pq (as in the RSA-based undeniable signature scheme). Let . Show that . [H] Argue that there are exactly four elements in of order ≤ 2. Let α ≢ ±1 (mod n) and ordn α < p′q′. Show that gcd(α – 1, n) or gcd(α + 1, n) is a non-trivial divisor of n. How many such elements α does contain? Let have order p′q′ or 2p′q′. Show that for every . Look at the denial protocol for the GKR RSA signature scheme (Algorithm 5.61) and assume that p′ < q′. Suppose that (M, s) is a forged signature (that is, s ∉ Sig M) on some message M with . Show that s ≡ αmd (mod n) for some with ordn α ≥ p′. Deduce that ordn(ms–e) ≥ p′. Conclude that if 4k < p′, then there exists a unique (namely, i′ = i) for which Congruence (5.11) holds.
5.24	Write the shortened versions of ECDSA signature generation and verification. Write the signcryption and unsigncryption algorithms based on shortened ECDSA.