A.2. Block Ciphers

Block ciphers encrypt plaintext messages in blocks of fixed lengths and are more ubiquitously used than public-key encryption routines. In a sense, public-key encryption is also block encryption. Since public-key routines are much slower than (secret-key) block ciphers, it is a custom to use public-key algorithms only in specific situations, for example, for encrypting single blocks of data, like keys of symmetric ciphers.

In the rest of this chapter, we use the word bit in the conventional sense, that is, to denote a quantity that can take only two possible values, 0 and 1. It is convenient to use the symbol to refer to the set {0, 1}. We also let stand for the set of all bit strings of length m. Whenever we plan to refer to the field (or group) structure of , we will use the alternative notation .

Definition A.1.

A block cipher f of block-size n and of key-size r is a map that encrypts a plaintext block m of bit length n to a ciphertext block c of bit length n under a key K, a bit string of length r. To ensure unique decryption, the map for a fixed key K has to be a permutation of (that is, a bijective function on) . In that case, the decryption of c to get back m is carried out as .

A good block cipher has the following desirable properties:

• The sizes n and r should be big enough, so that an adversary cannot exhaustively check all possibilities of m or K in feasible time.

• For most, if not all, keys K, the permutations f_K should be sufficiently random. In other words, if the key K is not known, it should be computationally infeasible to guess the functions f_K and 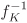. That is, it should be difficult to guess c from m or m from c, unless the key K is provided. The identity map on 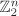, though a permutation of , is a bad candidate for an encryption function f_K. It is also desirable that the functions f_K for different values of K are unpredictably selected from the set of all permutations of 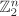. Thus, for example, taking f_K to be a fixed permutation for all choices of K leads to a poor design of a block cipher f.

• For most, if not all, pairs of distinct keys K₁ and K₂, the functions g_K1 ο g_K2 should not equal g_K for some key K, where g stands for f or f^–1 with independent choices in the three uses. A more stringent demand is that the subgroup generated by the permutations f_K for all possible keys K should be a very big subset of the group of all permutations of 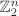. If g_K = g_K1 ο g_K2 ο · · · ο g_Kt for some t ≥ 2, multiple encryption (see Section A.3) forfeits its expected benefits.

A block cipher provably possessing all these good characteristics (in particular, the randomness properties) is difficult to construct in practice. Practical block ciphers are manufactured for reasonably big n and r and come with the hope of representing reasonably unpredictable permutations. We dub a block cipher good or safe, if it stands the test of time. Table A.1 lists some widely used block ciphers.

Table A.1. Some popular block ciphers

Name	n	r
DES (Data Encryption Standard)	64	56
FEAL (Fast Data Encipherment Algorithm)	64	64
SAFER (Secure And Fast Encryption Routine)	64	64
IDEA (International Data Encryption Algorithm)	64	128
Blowfish	64	≤ 448
Rijndael, accepted as AES (Advanced Encryption Standard) by NIST (National Institute of Standards and Technology, a US government organization)	128/192/256	128/192/256

A.2.1. A Case Study: DES

The data encryption standard (DES) was proposed as a federal information processing standard (FIPS) in 1975. DES has been the most popular and the most widely used among all block ciphers ever designed. Although its relatively small key-size offers questionable security under today’s computing power, DES still enjoys large-scale deployment in not-so-serious cryptographic applications.

DES encryption requires a 64-bit plaintext block m and a 56-bit key K.^[1] Let us plan to use the notations DES_K and to stand respectively for DES encryption and decryption functions under the key K.

^[1] A DES key K = k₁k₂ . . . k₆₄ is actually a 64-bit string. Only 56 bits of K are used for encryption. The remaining 8 bits are used as parity-check bits. Specifically, for each i = 1, . . . , 8 the bit k_8i is adjusted so that the i-th byte (k_{8i – 7}k_{8i – 6} . . . k_8i) has an odd number of one-bits.

DES key schedule

The DES algorithm first computes sixteen 48-bit keys K₁, K₂, . . . , K₁₆ from K using a procedure known as the DES key schedule described in Algorithm A.1. These 16 keys are used in the 16 rounds of encryption. The key schedule uses two fixed permutations PC1 and PC2 described after Algorithm A.1 and to be read in the row-major order. Here, PC is an abbreviation for permuted choice.

Algorithm A.1. The DES key schedule

Input: A DES key K = k1k2 . . . k64 (containing the parity-check bits). Output: Sixteen 48-bit round keys K1, K2, . . . , K16. Steps: Use PC1 to generate . Write U0 = C0 ‖ D0 with C0, . for i = 1, 2, . . . ,16 {    Take     Cyclically left shift Ci – 1 by s bits to get Ci.    Cyclically left shift Di – 1 by s bits to get Di.    Let .    Compute the i-th round key Ki := PC2(Ui) = u14u17u11 . . . u29u32. }

PC1
57	49	41	33	25	17	9
1	58	50	42	34	26	18
10	2	59	51	43	35	27
19	11	3	60	52	44	36
63	55	47	39	31	23	15
7	62	54	46	38	30	22
14	6	61	53	45	37	29
21	13	5	28	20	12	4

PC2
14	17	11	24	1	5
3	28	15	6	21	10
23	19	12	4	26	8
16	7	27	20	13	2
41	52	31	37	47	55
30	40	51	45	33	48
44	49	39	56	34	53
46	42	50	36	29	32

DES encryption

DES encryption, as described in Algorithm A.2, proceeds in 16 rounds. The i-th round uses the key K_i (obtained from the key schedule) in tandem with the encryption primitive e. A fixed permutation IP and its inverse IP^–1 are also used.^[2]

^[2] A block cipher that executes several encryption rounds with the i-th round computing the two halves as L_i := R_{i – 1} and R_i := L_{i – 1} ⊕ e(R_{i – 1}, K_i) for some round key K_i and for some encryption primitive e, is called a Feistel cipher. Most popular block ciphers mentioned earlier are of this type. Rijndael is an exception, and its acceptance as the new standard has been interpreted as an end of the Feistel dynasty.

It requires a specification of the round encryption function e to complete the description of DES encryption. The function e can be compactly depicted as:

e(X, J) := P(S(E(X) ⊕ J)),

Algorithm A.2. DES encryption

Input: Plaintext block m = m1m2 . . . m64 and the round keys K1, . . . , K16. Output: The ciphertext block . Steps: Apply the initial permutation on m to get       Write V = L0 ‖ R0 with L0, . for i = 1, 2, . . . , 16 {    /* The i-th encryption round */    Li := Ri – 1.    Ri := Li – 1 ⊕ e(Ri – 1, Ki). } Let . Apply the inverse of the initial permutation on W to get the ciphertext block    .

IP
58	50	42	34	26	18	10	2
60	52	44	36	28	20	12	4
62	54	46	38	30	22	14	6
64	56	48	40	32	24	16	8
57	49	41	33	25	17	9	1
59	51	43	35	27	19	11	3
61	53	45	37	29	21	13	5
63	55	47	39	31	23	15	7

IP–1
40	8	48	16	56	24	64	32
39	7	47	15	55	23	63	31
38	6	46	14	54	22	62	30
37	5	45	13	53	21	61	29
36	4	44	12	52	20	60	28
35	3	43	11	51	19	59	27
34	2	42	10	50	18	58	26
33	1	41	9	49	17	57	25

where is an expansion function, is a contraction function and P is a fixed permutation of (called the permutation function). S uses eight S-boxes (substitution boxes) S₁, S₂, . . . , S₈. Each S-box S_j is a 4 × 16 matrix with each row a permutation of 0, 1, 2, . . . , 15 and is used to convert a 6-bit string y₁y₂y₃y₄y₅y₆ to a 4-bit string z₁z₂z₃z₄ as follows. Let μ denote the integer with binary representation y₁y₆ and ν the integer with binary representation y₂y₃y₄y₅. Then, z₁z₂z₃z₄ is the 4-bit binary representation of the μ, ν-th entry in the matrix S_j. (Here, the numbering of the rows and columns starts from 0.) In this case, we write S_j(y₁y₂y₃y₄y₅y₆) = z₁z₂z₃z₄. Algorithm A.3 provides the description of e.

Algorithm A.3. The DES round encryption primitive e

Input: and . Output: e(X, J). Steps: Y := E(X) ⊕ J (where E(x1x2 . . . x32) = x32x1x2 . . . x32x1). Write Y = Y1 ‖ Y2 ‖ . . . ‖ Y8 with each . for  .  (where P(z1z2 . . . z32) = z16z7z20 . . . z4z25).

The tables for E and P are as follows.

E
32	1	2	3	4	5
4	5	6	7	8	9
8	9	10	11	12	13
12	13	14	15	16	17
16	17	18	19	20	21
20	21	22	23	24	25
24	25	26	27	28	29
28	29	30	31	32	1

P
16	7	20	21
29	12	28	17
1	15	23	26
5	18	31	10
2	8	24	14
32	27	3	9
19	13	30	6
22	11	4	25

Finally, the eight S-boxes are presented:

S1
14	4	13	1	2	15	11	8	3	10	6	12	5	9	0	7
0	15	7	4	14	2	13	1	10	6	12	11	9	5	3	8
4	1	14	8	13	6	2	11	15	12	9	7	3	10	5	0
15	12	8	2	4	9	1	7	5	11	3	14	10	0	6	13

S2
15	1	8	14	6	11	3	4	9	7	2	13	12	0	5	10
3	13	4	7	15	2	8	14	12	0	1	10	6	9	11	5
0	14	7	11	10	4	13	1	5	8	12	6	9	3	2	15
13	8	10	1	3	15	4	2	11	6	7	12	0	5	14	9

S3
10	0	9	14	6	3	15	5	1	13	12	7	11	4	2	8
13	7	0	9	3	4	6	10	2	8	5	14	12	11	15	1
13	6	4	9	8	15	3	0	11	1	2	12	5	10	14	7
1	10	13	0	6	9	8	7	4	15	14	3	11	5	2	12

S4
7	13	14	3	0	6	9	10	1	2	8	5	11	12	4	15
13	8	11	5	6	15	0	3	4	7	2	12	1	10	14	9
10	6	9	0	12	11	7	13	15	1	3	14	5	2	8	4
3	15	0	6	10	1	13	8	9	4	5	11	12	7	2	14

S5
2	12	4	1	7	10	11	6	8	5	3	15	13	0	14	9
14	11	2	12	4	7	13	1	5	0	15	10	3	9	8	6
4	2	1	11	10	13	7	8	15	9	12	5	6	3	0	14
11	8	12	7	1	14	2	13	6	15	0	9	10	4	5	3

S6
12	1	10	15	9	2	6	8	0	13	3	4	14	7	5	11
10	15	4	2	7	12	9	5	6	1	13	14	0	11	3	8
9	14	15	5	2	8	12	3	7	0	4	10	1	13	11	6
4	3	2	12	9	5	15	10	11	14	1	7	6	0	8	13

S7
4	11	2	14	15	0	8	13	3	12	9	7	5	10	6	1
13	0	11	7	4	9	1	10	14	3	5	12	2	15	8	6
1	4	11	13	12	3	7	14	10	15	6	8	0	5	9	2
6	11	13	8	1	4	10	7	9	5	0	15	14	2	3	12

S8
13	2	8	4	6	15	11	1	10	9	3	14	5	0	12	7
1	15	13	8	10	3	7	4	12	5	6	11	0	14	9	2
7	11	4	1	9	12	14	2	0	6	10	13	15	3	5	8
2	1	14	7	4	10	8	13	15	12	9	0	3	5	6	11

DES decryption

DES decryption is analogous to DES encryption. To obtain one first computes the round keys K₁, K₂, . . . , K₁₆ using Algorithm A.1. One then calls a minor variant of Algorithm A.2. First, the roles of m and c are interchanged. That is, one inputs c instead of m, and obtains m in place of c as output. Moreover, the right half R_i in the i-th round is computed as R_i := L_{i – 1} ⊕ e(R_{i – 1}, K_{17 – i}). In other words, DES decryption is same as DES encryption, only with the sequence of using the keys K₁, K₂, . . . , K₁₆ reversed. Solve Exercise A.1 in order to establish the correctness of this decryption procedure.

DES test vectors

Some test vectors for DES are given in Table A.2.

Table A.2. DES test vectors

Key	Plaintext block	Ciphertext block
0101010101010101	0000000000000000	8ca64de9c1b123a7
fefefefefefefefe	ffffffffffffffff	7359b2163e4edc58
3101010101010101	1000000000000001	958e6e627a05557B
1010101010101010	1111111111111111	f40379ab9e0ec533
0123456789abcdef	1111111111111111	17668dfc7292532d
1010101010101010	0123456789abcdef	8a5ae1f81ab8f2dd
fedcba9876543210	0123456789abcdef	ed39d950fa74bcc4

Cryptanalysis of DES

DES, being a popular block cipher, has gone through a good amount of cryptanalytic studies. At present, linear cryptanalysis and differential cryptanalysis are the most sophisticated attacks on DES. But the biggest problem with DES is its relatively small key size (56 bits). An exhaustive key search for a given plaintext–ciphertext pair needs carrying out a maximum of 2⁵⁶ encryptions in order to obtain the correct key. But how big is this number 2⁵⁶ = 72,057,594,037,927,936 (nearly 72 quadrillion) in a cryptographic sense?

In order to review this question, RSA Security Inc. posed several challenges for obtaining the DES key from given plaintext–ciphertext pairs. The first challenge, posed in January 1997, was broken by Rocke Verser of Loveland, Colorado, with approximately 96 days of computing. DES Challenge II-1 was broken in February 1998 by distributed.net with 41 days of computing, and the DES challenge II-2 was cracked in July 1998 by the Electronic Frontier Foundation (EFF) in just 56 hours. Finally, DES Challenge III was broken in a record of 22 hours 15 minutes in January 1999. The computations were carried out in EFF’s supercomputer Deep Crack with collaborative efforts from nearly 10⁵ PCs on the Internet guided by distributed.net. These figures demonstrate that DES offers hardly any security against a motivated adversary.

Another problem with DES is that its design criteria (most importantly, the objectives behind choosing the particular S-boxes) were never made public. Chances remain that there are hidden backdoors, though none has been discovered till date.

A.2.2. The Advanced Standard: AES

The advanced encryption standard (AES) [219] has superseded the older standard DES. The Rijndael cipher designed by Daemen and Rijmen has been accepted as the advanced standard. As mentioned in Footnote 2, Rijndael is not a Feistel cipher. Its working is based on the arithmetic in the finite field and in the finite ring .

Data representation

AES encrypts data in blocks of 128 bits. Let B = b₀b₁ . . . b₁₂₇ be a block of data, where each b_i is a bit. Keeping in view typical 32-bit processors, each such block B is represented as a sequence of four 32-bit words, that is, B = B₀B₁B₂B₃, where B_i represents the bit string b_32ib_32i+1 . . . b_32i+31. Each word C = c₀c₁ . . . c₃₁, in turn, is viewed as a sequence of four octets, that is, C = C₀C₁C₂C₃, where C_i stores the bit string c_8ic_8i+1 . . . c_8i+7. Each octet is identified as an element of , whereas an entire 32-bit word is identified with an element of .

The field is represented as , where f(X) is the irreducible polynomial X⁸ + X⁴ + X³ + X + 1. Let x := X + 〈f(X)〉. The element is identified with the octet d₇d₆ . . . d₁d₀. Thus, the i-th octet c_8ic_8i+1 . . . c_8i+7 in a word is treated as the finite field element .

Now, let us explain the interpretation of a 32-bit word C = C₀C₁C₂C₃. The -algebra is not a field, since the polynomial Y⁴ + 1 is reducible (over and so over ). However, each element β of A can be uniquely expressed as a polynomial β = α₃y³ + α₂y² + α₁y + α₀, where y := Y + 〈Y⁴ + 1〉 and where each α_i is an element of . As described in the last paragraph, each α_i is represented as an octet. We take C_i to be the octet representing α_{3 – i}, that is, the 32-bit word α₃α₂α₁α₀ stands for the element .

and A are rings and hence equipped with arithmetic operations (addition and multiplication). These operations are different from the usual addition and multiplication operations defined on octets and words. For example, the addition of two octets or words under the AES interpretation is the same as bit-wise XOR of octets or words. The AES multiplication of octets and words, on the other hand, involves polynomial arithmetic and reduction modulo the defining polynomials and so cannot be expressed so simply as addition. To resolve ambiguities, let us plan to denote the multiplication of by ⊙ and that of A by ⊗, whereas regular multiplication symbols (·, × and juxtaposition) stand for the standard multiplication on octets or words. Exercises A.5, A.6 and A.7 discuss about efficient implementations of the arithmetic in and A.

Every non-zero element is invertible; the inverse is denoted by α^–1 and can be computed by the extended gcd algorithm on polynomials over . With an abuse of notation, we take 0^–1 := 0. Every non-zero element of A is not invertible (under the multiplication of A). The AES algorithm uses the following invertible element β := 03010102 (in hex notation); its inverse is β^–1 = 0b0d090e.

The AES algorithm uses an object called a state, comprising 16 octets arranged in a 4 × 4 array. Each message block also consists of 16 octets. Let M = μ₀μ₁ . . . μ₁₅ be a message block (of 16 octets). This block is translated to a state as follows:

Equation A.1

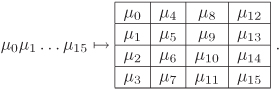
Thus, each word in the block is relocated in a column of the state. At the end of the encryption procedure, AES makes the reverse translation of a state to a block:

Equation A.2

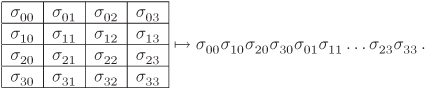
AES key schedule

A collection of round keys is generated from the given AES key K. The number of rounds of the AES encryption algorithm depends on the size of the key. Let us denote the number of words in the AES key by N_k and the corresponding number of rounds by N_r. We have:

One first generates an initial 128-bit key K₀K₁K₂K₃. Subsequently, for the i-th round, 1 ≤ i ≤ N_r, a 128-bit key K_4iK_4i+1K_4i+2K_4i+3 is required. Here, each K_j is a 32-bit word. The key schedule (also called key expansion) generates a total of 4(N_r + 1) words K₀, K₁, . . . , K_4Nr+3 from the given secret key K using a procedure described in Algorithm A.4. Here, (02)^{j – 1} stands for the octet that represents the element . The following table summarizes these values for j = 1, 2, . . . , 15.

j	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
xj – 1	01	02	04	08	10	20	40	80	1b	36	6c	d8	ab	4d	9a

The transformation SubWord on a word T = τ₀τ₁τ₂τ₃ is the octet-wise application of AES S-box substitution SubOctet, that is,

SubWord(T) = SubOctet(τ₀) ‖ SubOctet(τ₁) ‖ SubOctet(τ₂) ‖ SubOctet(τ₃).

Algorithm A.4. AES key schedule

Input: (Nk and) the secret key K = κ0κ1 ... κ4Nk – 1, where each κi is an octet. Output: The expanded keys K0, K1, . . . , K4Nr+3. Steps: /* Initially copy the bytes of K */ for i = 0, 1, . . . , Nk – 1 { Ki := κ4iκ4i+1κ4i+2κ4i+3. } /* Recursively define the round keys */ for i = Nk, Nk + 1, . . . , 4Nr + 3 {       T := Ki – 1;       /* T is a temporary word variable. */       /* Let T = τ0τ1τ2τ3, where each τi is an octet. */       if (i rem Nk = 0) { T := SubWord(τ1τ2τ3τ0) ⊕ [(02)(i/Nk) – 1‖000000]. }       else if (Nk > 6) and (i rem Nk = 4) { T := SubWord(T). }       Ki := Ki – Nk ⊕ T. }

The transformation SubOctet is also used in each encryption round and is now described. Let A = a₀a₁ . . . a₇ be an octet that can be identified with an element of as mentioned earlier. Let B = b₀b₁ . . . b₇ denote the octet representing the inverse of this finite field element. (We take 0^–1 = 0.) One then applies the following affine transformation on B to generate the final value C := SubOctet(A) := c₀c₁ . . . c₇. Here, D = d₀d₁ . . . d₇ is the constant octet 63 = 01100011.

Equation A.3

In order to speed up this octet substitution, one may use table lookup. Since the output octet C depends only on the input octet A, one can precompute a table of values of SubOctet(A) for the 256 possible values of A. This list is given in Table A.3. The table is to be read in the row-major fashion. In other words, if hi and lo respectively represent the most and the least significant four bits of A, then SubOctet(A) can be read off from the entry in the table having row number hi and column number lo. For example, SubOctet(a7) = 5c. In an actual implementation, a one-dimensional array is to be used. We use a two-dimensional format in Table A.3 for the sake of clarity of presentation.

Table A.3. AES S-box

	0	1	2	3	4	5	6	7	8	9	a	b	c	d	e	f
0	63	7c	77	7b	f2	6b	6f	c5	30	01	67	2b	fe	d7	ab	76
1	ca	82	c9	7d	fa	59	47	f0	ad	d4	a2	af	9c	a4	72	c0
2	b7	fd	93	26	36	3f	f7	cc	34	a5	e5	f1	71	d8	31	15
3	04	c7	23	c3	18	96	05	9a	07	12	80	e2	eb	27	b2	75
4	09	83	2c	1a	1b	6e	5a	a0	52	3b	d6	b3	29	e3	2f	84
5	53	d1	00	ed	20	fc	b1	5b	6a	cb	be	39	4a	4c	58	cf
6	d0	ef	aa	fb	43	4d	33	85	45	f9	02	7f	50	3c	9f	a8
7	51	a3	40	8f	92	9d	38	f5	bc	b6	da	21	10	ff	f3	d2
8	cd	0c	13	ec	5f	97	44	17	c4	a7	7e	3d	64	5d	19	73
9	60	81	4f	dc	22	2a	90	88	46	ee	b8	14	de	5e	0b	db
a	e0	32	3a	0a	49	06	24	5c	c2	d3	ac	62	91	95	e4	79
b	e7	c8	37	6d	8d	d5	4e	a9	6c	56	f4	ea	65	7a	ae	08
c	ba	78	25	2e	1c	a6	b4	c6	e8	dd	74	1f	4b	bd	8b	8a
d	70	3e	b5	66	48	03	f6	0e	61	35	57	b9	86	c1	1d	9e
e	e1	f8	98	11	69	d9	8e	94	9b	1e	87	e9	ce	55	28	df
f	8c	a1	89	0d	bf	e6	42	68	41	99	2d	0f	b0	54	bb	16

AES encryption

AES encryption is described in Algorithm A.5. The algorithm first converts the input plaintext message block to a state, applies a series of transformations on this state and finally converts the state back to a message (the ciphertext).

The individual state transition transformations are now explained. The transition SubState is an octet-by-octet application of the substitution function SubOctet, that is, SubState maps

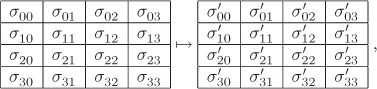
where for all r, c. The transform ShiftRows cyclically left rotates the r-th row by r byte positions, that is, maps

The AddKey operation uses four 32-bit round keys L₀, L₁, L₂, L₃. Name the octets of L_i as λ_i0λ_i1λ_i2λ_i3. The i-th key L_i is XORed with the i-th column of the state, that is, AddKey transforms

Finally, the MixCols transform multiplies each column of the state, regarded as an element of , by the element , where the coefficients (expressions within square brackets) are octet values in hexadecimal, that can be identified with elements of . For the c-th column, this transformation can be represented as:

Algorithm A.5. AES encryption

Input: The plaintext message M = μ0μ1 . . . μ15 and the round keys K0, K1, . . . , K4Nr+3. Output: Ciphertext message C = γ0γ1 . . . γ15. Steps: Convert M to the state S.                                      /* Use Transform (A.1) */ S := AddKey(S, K0, K1, K2, K3). for i = 1, 2, . . . , Nr {       S := SubState(S).       S := ShiftRows(S).       if (i ≠ Nr) { S := MixCols(S). }       S := AddKey(S, K4i, K4i+1, K4i+2, K4i+3). } Convert S to the message C.                                /* Use Transform (A.2) */

AES decryption

AES decryption involves taking inverse of each state transition performed during encryption. The key schedule needed for encryption is to be used during decryption too. The straightforward decryption routine is given in Algorithm A.6.

Algorithm A.6. AES decryption

Input: The ciphertext message C = γ0γ1 . . . γ15 and the round keys K0, K1, . . . , K4Nr+3. Output: The recovered plaintext message M = μ0μ1 . . . μ15. Steps: Convert C to the state S.                                      /* Use Transform (A.1) */ S := AddKey(S, K4Nr, K4Nr+1, K4Nr+2, K4Nr+3). for i = Nr – 1, Nr – 2, . . . , 1, 0 {       S := ShiftRows–1(S).       S := SubState–1(S).       S := AddKey(S, K4i, K4i+1, K4i+2, K4i+3).       if (i ≠ 0) { S := MixCols–1(S). } } Convert S to the message M.                                /* Use Transform (A.2) */

What remains is a description of the inverses of the basic state transformations. AddKey involves octet-by-octet XORing and so is its own inverse. Table A.4 summarizes the inverse of the substitution transition SubOctet (Exercise A.8). For computing SubState^–1(S), one should apply SubOctet^–1 on each octet of S. The inverse of ShiftRows is also straightforward and can be given by

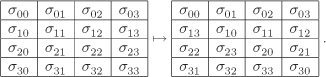
Finally, MixCols^–1 involves multiplication of each column by the inverse of the element , that is, by the element [0b]y³ + [0d]y² + [09]y + [0e]. So MixCols^–1 transforms each column of the state as follows:

Table A.4. Inverse of AES S-box

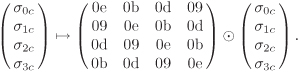
	0	1	2	3	4	5	6	7	8	9	a	b	c	d	e	f
0	52	09	6a	d5	30	36	a5	38	bf	40	a3	9e	81	f3	d7	fb
1	7c	e3	39	82	9b	2f	ff	87	34	8e	43	44	c4	de	e9	cb
2	54	7b	94	32	a6	c2	23	3d	ee	4c	95	0b	42	fa	c3	4e
3	08	2e	a1	66	28	d9	24	b2	76	5b	a2	49	6d	8b	d1	25
4	72	f8	f6	64	86	68	98	16	d4	a4	5c	cc	5d	65	b6	92
5	6c	70	48	50	fd	ed	b9	da	5e	15	46	57	a7	8d	9d	84
6	90	d8	ab	00	8c	bc	d3	0a	f7	e4	58	05	b8	b3	45	06
7	d0	2c	1e	8f	ca	3f	0f	02	c1	af	bd	03	01	13	8a	6b
8	3a	91	11	41	4f	67	dc	ea	97	f2	cf	ce	f0	b4	e6	73
9	96	ac	74	22	e7	ad	35	85	e2	f9	37	e8	1c	75	df	6e
a	47	f1	1a	71	1d	29	c5	89	6f	b7	62	0e	aa	18	be	1b
b	fc	56	3e	4b	c6	d2	79	20	9a	db	c0	fe	78	cd	5a	f4
c	1f	dd	a8	33	88	07	c7	31	b1	12	10	59	27	80	ec	5f
d	60	51	7f	a9	19	b5	4a	0d	2d	e5	7a	9f	93	c9	9c	ef
e	a0	e0	3b	4d	ae	2a	f5	b0	c8	eb	bb	3c	83	53	99	61
f	17	2b	04	7e	ba	77	d6	26	e1	69	14	63	55	21	0c	7d

AES decryption is as efficient as AES encryption, since each state transformation primitive has the same structure as its inverse. However, the sequence of application of these primitives in the loop (rounds) for decryption differs from that for encryption. For some implementations, mostly in hardware, this may be a problem. Compare this with DES for which the encryption and decryption algorithms are identical save the sequence of using the round keys (Exercise A.1). With little additional effort AES can also be furnished with this useful property of DES. All we have to do is to use a different key schedule for decryption. The necessary modifications are explored in Exercise A.9.

AES test vectors

Table A.5 provides the ciphertexts for the plaintext block

M = 00112233445566778899aabbccddeeff

under different keys.

Table A.5. AES test vectors

Cipher	Key	Ciphertext block
AES-128	0001020304050607 08090a0b0c0d0e0f	69c4e0d86a7b0430 d8cdb78070b4c55a
AES-192	0001020304050607 08090a0b0c0d0e0f 1011121314151617	dda97ca4864cdfe0 6eaf70a0ec0d7191
AES-256	0001020304050607 08090a0b0c0d0e0f 1011121314151617 18191a1b1c1d1e1f	8ea2b7ca516745bf eafc49904b496089

Cryptanalysis of AES

AES has been designed so that linear and differential attacks are infeasible. Another attack known as the square attack has been proposed by Lucks [184] and Ferguson et al. [93], but at present can tackle less number of rounds than used in Rijndael encryption. Also see Gilbert and Minier [112] to know about the collision attack.

The distinct algebraic structure of AES encryption invites special algebraic attacks. One such potential attack (the XSL attack) has been proposed by Courtois and Pieprzyk [68]. Although this attack has not yet been proved to be effective, a better understanding of the algebra may, in foreseeable future, lead to disturbing consequences for the advanced standard.

For more information on AES, read the book [71] from the designers of the cipher. Also visit the following Internet sites:

http://www.esat.kuleuven.ac.be/~rijmen/rijndael/	Rijndael home
http://csrc.nist.gov/CryptoToolkit/aes/index1.html	NIST site for AES
http://www.cryptosystem.net/aes/	Algebraic attacks

A.2.3. Multiple Encryption

Multiple encryption presents a way to achieve a desired level of security by using block ciphers of small key sizes. The idea is to cascade several stages of encryption and/or decryption, with different stages working under different keys. Figure A.1 illustrates double and triple encryption for a block cipher f. Each g_i or h_j represents either the encryption or the decryption function of f under the given key.

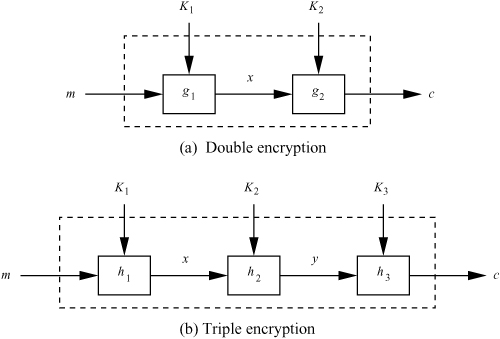
For double encryption, we have K₁ ≠ K₂ and both g₁ and g₂ are usually the encryption function. Unless f_K2 ο f_K1 is the same as f_K for some key K and if the permutations of f are reasonably random, it appears at the first glance that double encryption increases the effective key size by a factor of two. Unfortunately, this is not the case. The meet-in-the-middle attack on double encryption works as follows.

Suppose that an adversary knows a plaintext–ciphertext pair (m, c) under the unknown keys K₁, K₂. We assume as before that f has block-size n and key-size r. The adversary computes for each possibility of the encrypted message x_i := f_i(m). She also computes for each the decrypted message . Now, (i, j) is a possible value of (K₁, K₂) if and only if .

A given pair (m, c) usually gives many such candidates (i, j) for (K₁, K₂). More precisely, if each is assumed to be a random permutation of , for a given i we have the equality for an expected number of 2^r/2ⁿ values of j. Considering all possibilities for i gives an expected number of 2^r × 2^r/2ⁿ = 2^{2r – n} candidate pairs (i, j). If f = DES, this number is 2^{2 × 56–64} = 2⁴⁸.

If a second pair (m′, c′) under (K₁, K₂) is also known to the adversary, then for a given i the pair (i, j) is consistent with both (m, c) and (m′, c′) with probability 2^r/(2ⁿ × 2ⁿ). Thus, we get an expected number of (2^r × 2^r)/(2ⁿ × 2ⁿ) = 2^{2r – 2n} candidates (i, j). For DES, this number is 2^–16. This implies that it is very unlikely that a false candidate (i, j) satisfies both (m, c) and (m′, c′). Thus, with high probability the adversary uniquely identifies the double DES key (K₁, K₂) from two plaintext–ciphertext pairs.

This attack calls for O(2^r) encryptions and O(2^r) decryptions. With the assumption that each encryption takes roughly the same time as each decryption (as in the case of DES), the adversary spends a time for O(2^r) encryptions. Moreover, she can find all the matches in O(r2^r) time. This implies that double encryption increases the effective key size (over single encryption) by a few bits only. On the other hand, both the actual key size and the encryption time get doubled. In view of these shortcomings, double encryption is rarely used in practice.

For the triple encryption scheme of Figure A.1, a meet-in-the-middle attack at x or y demands an effort equivalent to O(2^2r) encryptions, that is, the effective key size gets doubled. It is, therefore, customary to take K₁ = K₃ and K₂ different from this common value. The actual key size also gets doubled with this choice—one doesn’t have to remember K₃ separately. It is also a common practice to take h₁ and h₃ the encryption function (under K₁ = K₃) and h₂ the decryption function (under K₂). One often calls this particular triple encryption an E-D-E scheme.

A.2.4. Modes of Operation

In practice, the length of the message m to be encrypted need not equal the block length n of the block cipher f. One then has to break up m into blocks of some fixed length n′ ≤ n and encrypt each block using the block cipher. In order to make the length of m an integral multiple of n′, one may have to pad extra bits to m (say, zero bits at the end). It is often necessary to store the initial size of m in a separate block, say, after the last message block. In what follows, we shall assume that the input message m gives rise to l blocks m₁, m₂, . . . , m_l each of size n′. The corresponding ciphertext blocks c₁, c₂, . . . , c_l will also be of bit length n′ each. The reason for choosing the block size n′ ≤ n will be clear soon.

The ECB mode

The easiest way to encrypt multiple blocks m₁, . . . , m_l is to take n′ = n and encrypt each block m_i as c_i := f_K(m_i). Decryption is analogous: . This mode of operation of a block cipher is called the electronic code-book or the ECB mode. Algorithms A.7 and A.8 describe this mode.

Algorithm A.7. ECB encryption

Input: The plaintext blocks m1, . . . , ml and the key K. Output: The ciphertext c = c1 . . . cl. Steps: for i = 1, . . . , l { ci := fK(mi) }

Algorithm A.8. ECB decryption

Input: The ciphertext blocks c1, . . . , cl and the key K. Output: The plaintext m = m1 . . . ml. Steps: for

In this mode, identical message blocks encrypt to identical ciphertext blocks (under the same key), that is, partial information about the plaintext may be leaked out. The following three modes overcome this problem.

The CBC mode

In the cipher-block chaining or the CBC mode, one takes n′ = n and each plaintext block is first XOR-ed with the previous ciphertext block and then encrypted. In order to XOR the first plaintext block, one needs an n-bit initialization vector (IV). The IV need not be kept secret and may be sent along with the ciphertext blocks.

Algorithm A.9. CBC encryption

Input: The plaintext blocks m1, . . . , ml, the key K and the IV. Output: The ciphertext c = c1 . . . cl. Steps: c0 := IV. for i = 1, . . . , l { ci := fK(mi ⊕ ci – 1). }

Algorithm A.10. CBC decryption

Input: The ciphertext blocks c1, . . . , cl, the key K and the IV. Output: The plaintext m = m1 . . . ml. Steps: c0 := IV. for

The CFB mode

In the cipher feedback or the CFB mode, one chooses . In this mode, the plaintext blocks are not encrypted, but masked by XOR-ing with a stream of random keys generated from a (not necessarily secret) n-bit IV. In this sense, the CFB mode works like a stream cipher (see Section A.3).

Algorithm A.11. CFB encryption

Input: The plaintext blocks m1, . . . , ml, the key K and the IV. Output: The ciphertext c = c1 . . . cl. Steps: k0 := IV.   /* Initialize the key stream */ for i = 1, . . . , l {    /* Mask the current key by block encryption and the message by XOR-ing */    ci := mi ⊕ msbn′ (fK(ki – 1)).    /* Generate the next key from the previous key and the current ciphertext block */    ki := lsbn – n′ (ki – 1) ‖ ci. }

Algorithm A.11 explains CFB encryption. The notation msb_k(z) (resp. lsb_k(z)) stands for the most (resp. least) significant k bits of a bit string z. For CFB decryption (Algorithm A.12), the identical key stream k₀, k₁, . . . , k_l is generated and used to mask off the message blocks from the ciphertext blocks.

Algorithm A.12. CFB decryption

Input: The ciphertext blocks c1, . . . , cl, the key K and the IV. Output: The plaintext m = m1 . . . ml. Steps: k0 := IV. for i = 1, . . . , l {    mi := ci ⊕ msbn′ (fK(ki – 1)).    ki := lsbn – n′ (ki – 1) ‖ ci. }

The OFB mode

The output feedback or the OFB mode also works like a stream cipher by masking the plaintext blocks using a stream of keys. The key stream in the OFB mode is generated by successively applying the block encryption function on an n-bit (not necessarily secret) IV. Here, one chooses any .

OFB encryption is explained in Algorithm A.13. OFB decryption (Algorithm A.14) is identical, with only the roles of m and c interchanged, and requires the generation of the same key stream k₀, k₁, . . . , k_l used during encryption.

Algorithm A.13. OFB encryption

Input: The plaintext blocks m1, . . . , ml, the key K and the IV. Output: The ciphertext c = c1 . . . cl. Steps: k0 := IV.      /* Initialize the key stream */ for i = 1, . . . , l {     ki := fK(ki–1).     /* Generate the next key in the stream */     ci := mi ⊕ msbn′ (ki)    . /* Mask the plaintext block */ }

Algorithm A.14. OFB decryption

Input: The ciphertext blocks c1, . . . , cl, the key K and the IV. Output: The plaintext m = m1 . . . ml. Steps: k0 := IV.     /* Initialize the key stream */ for i = 1, . . . , l {    ki := fK(ki–1).    /* Generate the next key in the stream */    mi := ci ⊕ msbn′ (ki).    /* Remove the mask from the ciphertext block */ }

Exercise Set A.2

A.1	Let us use the notations of Algorithm A.2. For a message m and round keys Ki, we have the values V, Li, Ri, W, c. For another message m′ and another set of round keys , let us denote these values by V′, , , W′, c′. Show that if m′ = c and if for i = 1, . . . , 16, then and for all i = 0, 1, . . . , 16. Deduce that in this case we have c′ = m. (This shows that DES decryption is the same as DES encryption with the key schedule reversed.)
A.2	For a bit string z, let denote the bit-wise complement of z. Deduce that , that is, complementing both the plaintext message and the key complements the ciphertext message. [H]
A.3	A DES key K is said to be weak, if the DES key schedule on K gives K1 = K2 = · · · = K16. Show that there are exactly four weak DES keys which in hexadecimal notation are: 0101 0101 0101 0101 FEFE FEFE FEFE FEFE 1F1F 1F1F 0E0E 0E0E E0E0 E0E0 F1F1 F1F1
A.4	A DES key K is said to be anti-palindromic, if the DES key schedule on K gives for all i = 1, . . . , 16. Show that the following four DES keys (in hexadecimal notation) are anti-palindromic: 01FE 01FE 01FE 01FE FE01 FE01 FE01 FE01 1FE0 1FE0 0EF1 0EF1 E01F E01F F10E F10E
A.5	Represent , where f(X) = X8 + X4 + X3 + X + 1 (Section A.2.2). Show that multiplication by x (the octet 02) in can be computed by a left shift followed conditionally (derive the condition) by XORing with the octet 1b. Design an algorithm for multiplying two elements of using bit manipulations on octets only.
A.6	The multiplication of can be made table-driven. Since this field contains 256 elements, a 256 × 256 array suffices to store all the products. That requires a storage of 64 kb. We can considerably reduce the storage by using discrete logs. Show that the multiplicative order of x (in ) is 51. Show that x + 1 is a generator of . Write a computer program to generate the table of discrete logarithms of elements of to the base x + 1 (Table A.6). Table A.6. Discrete-log table for AES   0 1 2 3 4 5 6 7 8 9 a b c d e f 0 – 00 19 01 32 02 1a c6 4b c7 1b 68 33 ee df 03 1 64 04 e0 0e 34 8d 81 ef 4c 71 08 c8 f8 69 1c c1 2 7d c2 1d b5 f9 b9 27 6a 4d e4 a6 72 9a c9 09 78 3 65 2f 8a 05 21 0f e1 24 12 f0 82 45 35 93 da 8e 4 96 8f db bd 36 d0 ce 94 13 5c d2 f1 40 46 83 38 5 66 dd fd 30 bf 06 8b 62 b3 25 e2 98 22 88 91 10 6 7e 6e 48 c3 a3 b6 1e 42 3a 6b 28 54 fa 85 3d ba 7 2b 79 0a 15 9b 9f 5e ca 4e d4 ac e5 f3 73 a7 57 8 af 58 a8 50 f4 ea d6 74 4f ae e9 d5 e7 e6 ad e8 9 2c d7 75 7a eb 16 0b f5 59 cb 5f b0 9c a9 51 a0 a 7f 0c f6 6f 17 c4 49 ec d8 43 1f 2d a4 76 7b b7 b cc bb 3e 5a fb 60 b1 86 3b 52 a1 6c aa 55 29 9d c 97 b2 87 90 61 be dc fc bc 95 cf cd 37 3f 5b d1 d 53 39 84 3c 41 a2 6d 47 14 2a 9e 5d 56 f2 d3 ab e 44 11 92 d9 23 20 2e 89 b4 7c b8 26 77 99 e3 a5 f 67 4a ed de c5 31 fe 18 0d 63 8c 80 c0 f7 70 07 Write a computer program to generate the table of powers of x + 1 (Table A.7). Table A.7. Power table for AES   0 1 2 3 4 5 6 7 8 9 a b c d e f 0 01 03 05 0f 11 33 55 ff 1a 2e 72 96 a1 f8 13 35 1 5f e1 38 48 d8 73 95 a4 f7 02 06 0a 1e 22 66 aa 2 e5 34 5c e4 37 59 eb 26 6a be d9 70 90 ab e6 31 3 53 f5 04 0c 14 3c 44 cc 4f d1 68 b8 d3 6e b2 cd 4 4c d4 67 a9 e0 3b 4d d7 62 a6 f1 08 18 28 78 88 5 83 9e b9 d0 6b bd dc 7f 81 98 b3 ce 49 db 76 9a 6 b5 c4 57 f9 10 30 50 f0 0b 1d 27 69 bb d6 61 a3 7 fe 19 2b 7d 87 92 ad ec 2f 71 93 ae e9 20 60 a0 8 fb 16 3a 4e d2 6d b7 c2 5d e7 32 56 fa 15 3f 41 9 c3 5e e2 3d 47 c9 40 c0 5b ed 2c 74 9c bf da 75 a 9f ba d5 64 ac ef 2a 7e 82 9d bc df 7a 8e 89 80 b 9b b6 c1 58 e8 23 65 af ea 25 6f b1 c8 43 c5 54 c fc 1f 21 63 a5 f4 07 09 1b 2d 77 99 b0 cb 46 ca d 45 cf 4a de 79 8b 86 91 a8 e3 3e 42 c6 51 f3 0e e 12 36 5a ee 29 7b 8d 8c 8f 8a 85 94 a7 f2 0d 17 f 39 4b dd 7c 84 97 a2 fd 1c 24 6c b4 c7 52 f6 01 Design an algorithm for multiplying two elements of using table lookup.
A.7	Denote the multiplication of by ⊗ (Section A.2.2). Let α = a3y3 + a2y2 + a1y + a0 and β = b3y3 + b2y2 + b1y + b0 be elements of A and γ = c3y3 + c2y2 + c1y + c0 = α ⊗ β. Show that where the matrix arithmetic on the right side follows the arithmetic of . Verify that the inverse of the element of A represented by the word 03010102 (in hex) is 0b0d090e.
A.8	Show that Transform (A.3) can be represented as where the matrix arithmetic on the right side is that of . Let denote the 8 × 8 matrix of Part (a). Prove that is invertible over with Conclude that the transformation A ↦ SubOctet(A) is invertible.
A.9	Argue that the transforms SubState and ShiftRows commute with one another. Show that MixCols–1(AddKey(S, L0, L1, L2, L3)) = AddKey(MixCols–1(S), MixCols–1(L0, L1, L2, L3)) for a suitable meaning of the application of MixCols–1 on four 32-bit keys L0, L1, L2 and L3. Conclude that one can obtain a decryption key schedule in such a way that Algorithm A.15 correctly performs AES decryption. [H] Algorithm A.15. Equivalent form of AES decryption Input: The ciphertext message C = γ0γ1 . . . γ15 and the decryption key schedule . Output: Plaintext message M = μ0μ1 . . . μ15. Steps: Convert C to the state S.                                 /* Use Transform (A.1) */ for i = Nr – 1, Nr – 2, . . . , 0 {       S := SubState–1(S).       S := ShiftRows–1(S).       if (i ≠ 0) { S := MixCols–1(S). }        } Convert S to the message M.                            /* Use Transform (A.2) */
A.10	Show that a multiple encryption scheme with exactly k stages provides an effective security of ⌈k/2⌉ keys against the meet-in-the-middle attack.
A.11	Consider a message m broken into blocks m1, . . . , ml, encrypted to c1, . . . , cl and sent to an entity. Suppose that during the transmission exactly one ciphertext block gets corrupted. Show that for the different modes of encryption, the numbers ν of blocks that are incorrectly decrypted due to this transmission error are as listed in the following table. Mode ν ECB 1 CBC ≤ 2 CFB ≤ 1 + ⌈n/n′⌉ OFB 1 For each of the four modes, discuss the effects on decryption caused by the insertion or deletion of a ciphertext block during transmission (say, by an active adversary).