Equations (3-10)and (3-11) |
Batch formulas for 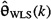 and and 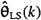 |
Theorem 4-1 |
Singular value decomposition of a rectangular matrix. |
Theorem 4-2 |
How to compute 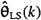 by singular value decomposition. by singular value decomposition. |
Theorem 4-3 |
How to compute 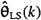 by singular value decomposition in the overdetermined case. by singular value decomposition in the overdetermined case. |
Theorem 4-4 |
Pseudoinverse of a full-rank matrix. |
Theorem 4-5 |
Computation of the pseudoinverse by singular value de-composition. |
Theorem 5-1 |
Information form of recursive LSE. |
Lemma 5-1 |
Matrix inversion lemma. |
Theorem 5-2 |
Covariance form of recursive LSE. |
Theorem 6-1 |
Sufficient conditions for a linear batch estimator to be unbiased. |
Theorem 6-2 |
Sufficient condition for a linear recursive estimator to be unbiased. |
Theorem 6-3 |
Cramer-Rao inequality for a scalar parameter. |
Corollary 6-1 |
Achieving the Cramer-Rao lower bound. |
Theorem 6-4 |
Cramer-Rao inequality for a vector of parameters. |
Corollary 6-2 |
Lower bound for error- variance of fth parameter. |
Theorem 7-1 |
Mean-squared convergence implies convergence in probability. |
Theorem 7-2 |
Conditions under which 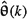 is a consistent estimator of θ is a consistent estimator of θ |
Theorem 8-1 |
Sufficient conditions for 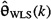 to be an unbiased estimator of θ to be an unbiased estimator of θ |
Theorem 8-2 |
A formula for cov[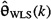 ] ] |
Corollary 8-1 |
A formula for cov[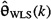 ] underspecial conditions on the measurement noise, and when H(k) is deterministic ] underspecial conditions on the measurement noise, and when H(k) is deterministic |
Theorem 8-3 |
Efficiency of the least-squares estimator within the class of linear estimators. |
Theorem 8-4 |
An unbiased estimator of  . . |
Theorem 8-5 |
Sufficient conditions for 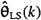 to be a consistent estimator of θ. to be a consistent estimator of θ. |
Theorem 8-6 |
Consistency of the instrumental variable least-squares estimator. |
Theorem 8-7 |
Sufficient conditions for 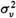 (k) to be a consistent estimator of (k) to be a consistent estimator of  . . |
Equation (9-24) |
Bath formula for 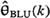 . . |
Theorem 9-1 |
The relationship between 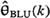 . . |
Corollary 9-1 |
When all the results obtained in Lessons 3, 4. and 5 for 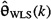 can be applied to can be applied to 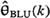 . . |
Theorem 9-2 |
When 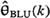 equals equals 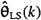 (Gauss-Markov theorem). (Gauss-Markov theorem). |
Theorem 9-3 |
A formula for cov 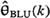 . . |
Corollary 9-2 |
The equivalence between P(k) and cov [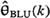 ] ] |
Theorem 9-4 |
Most efficient estimator property of 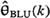 within the class of linear estimators. within the class of linear estimators. |
Corollary 9-3 |
When 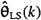 is a most efficient estimator of θ. is a most efficient estimator of θ. |
Theorem 9-5 |
Invariance of 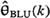 to scale changes. to scale changes. |
Theorem 9-6 |
Information form of recursive BLUE. |
Theorem 9-7 |
Covariance form of recursive BLUE. |
Definition 10-1 |
Likelihood defined. |
Theorem 10-1 |
Likelihood ratio of combined data from statistically independent sets of data. |
Theorem 11-1 |
Large-sample properties of maximum-likelihood estimates. |
Theorem 11-2 |
Invariance property of MLEs. |
Theorem 11-3 |
Condition under which 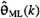 = = 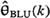 and resulting estimator properties. and resulting estimator properties. |
Corollary 11-1 |
Conditions under which 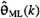 = = 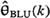 (&) = (&) = 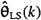 , and resulting estimator properties. , and resulting estimator properties. |
Theorem 12-1 |
A formula for p(x|y) when x and y are jointly Gaussian. |
Theorem 12-2 |
Properties of E{x|y} when x and y are jointly Gaussian. |
Theorem 12-3 |
Expansion formula for E{x|y, z} when x, y, and z are jointly Gaussian and y and z are statistically independent. |
Theorem 12-4 |
Expansion formula for E{x|y, z} when x, y, and z are jointly Gaussian and y and z are not necessarily statistically independent. |
Theorem 13-1 |
A formula for 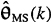 (the fundamental theorem of estimation theory). (the fundamental theorem of estimation theory). |
Corollary 13-1 |
A formula for 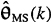 when θ and Z(k) are jointly Gaussian. when θ and Z(k) are jointly Gaussian. |
Corollary 13-2 |
A linear mean-squared estimator of θ in the non-Gaussian case. |
Corollary 13-3 |
Orthogonality principle. |
Theorem 13-2 |
Mean-squared estimator for the generic linear and Gaussian model. |
Theorem 13-3 |
Conditions under which 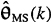 = = 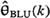 . . |
Theorem 13-4 |
Conditions under which 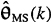 = = 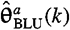 . . |
Theorem 14-1 |
When 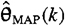 = = 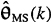 . . |
Theorem 14-2 |
Conditions under which 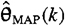 = = 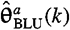 . . |
Theorem 14-3 |
Equality of probability of detection and unconditional maximum-likelihood detection rules. |
Theorem 15-1 |
Expansion of ajoint probability density function for a first-order Markov process. |
Theorem 15-2 |
Calculation of conditional expectation for a first-order Markov process. |
Theorem 15-3 |
Interpretation of Gaussian white noise as a special first-order Markov process. |
Equations(15-17) and (15-18) |
The basic state-variable model. |
Theorem 15-4 |
Conditions under which x(k) is a Gauss-Markov sequence. |
Theorem 15-5 |
Recursive equations for computing mx(k) and Px(k). |
Theorem 15-6 |
Formulas for computing mz(k) and Pz(k). |
Equations (16-4) and (16-11) |
Single-stage predictor formulas for  and P(kk-l). and P(kk-l). |
Theorem 16-1 |
Formula for and properties of general state predictor 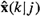 ,k > j. ,k > j. |
Theorem 16-2 |
Representations and properties of the innovations process. |
Theorem 17-1 |
Kalman filter formulas and properties of resulting estimates and estimation error. |
Theorem 19-1 |
Steady-state Kalman filter. |
Theorem 19-2 |
Equivalence of steady-state Kalman filter and infinitelength digital Wiener filter. |
Supplement to Lesson 19 |
Levinson algorithm. |
Theorem 20-1 |
Single-state smoother formula for  . . |
Corollary 20-1 |
Relationship between single-stage smoothing gain matrix and Kalman gain matrix. |
Corollary 20-2 |
Another way to express  . . |
Theorem 20-2 |
Double-stage smoother formula for 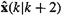 . . |
Corollary 20-3 |
Relationship between double-stage smoothing gain matrix and Kalman gain matrix. |
Corollary 20-4 |
Two other ways to express 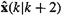 . . |
Theorem 21-1 |
Formulas for a useful fixed-interval smoother of x(k), 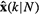 , and its error-covariance matrix, P(kN). , and its error-covariance matrix, P(kN). |
Theorem 21-2 |
Formulas for a most useful two-pass fixed-interval smoother of x(k), 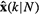 , and its associated error- covariance matrix, P(kN). , and its associated error- covariance matrix, P(kN). |
Theorem 21-3 |
Formulas for a most useful fixed-point smoothed estimator of x(k),  , where l = 1, 2,…, and its associated error-covariance matrix, P(kk + l). , where l = 1, 2,…, and its associated error-covariance matrix, P(kk + l). |
Theorem 21-4 |
Conditions under which a single-channel state-variable model is equivalent to a convolutional sum model. |
Theorem 21-5 |
Recursive minimum-variance deconvolution formulas. |
Theorem 21-6 |
Steady-state MVD filter and zero phase nature of estimated signal component of system input. |
heorem 21-7 |
Equivalence between steady-state MVD filter and Berkhout’s infinite impulse response digital Wiener deconvolution filter. |
Theorem 21-8 |
Maximum-likelihood deconvolution results. |
Theorem 22-1 |
How to handle biases that may be present in a state-variable model. |
Theorem 22-2 |
Predictor-corrector Kalman filter for the correlated noise case. |
Corollary 22-1 |
Recursive predictor formulas for the correlated noise case. |
Corollary 22-2 |
Recursive filter formulas for the correlated noise case. |
Theorem 22-3 |
An identity involving the innovations. |
Equations (23-1) and (23-2) |
Nonlinear state-variable model. |
Equations (23-23) and (23-30) |
Perturbation state-variable model. |
Theorem 23-1 |
Solution to a time-varying continuous-time state equation. |
Equations (23-39) and (23-44) |
Discretized state-variable model. |
Theorem 24-1 |
A consequence of relinearizing about  . . |
Equations (24-22) and (24-27) |
Extended Kalman filter prediction and correction equations for a nonlinear continuous-time system. |
Equations (24-44) and (24-47) |
Extended Kalman filter prediction and correction equations for a nonlinear discrete-time system. |
Theorem 25-1 |
Formula for the log-likelihood function of the basic state-variable model. |
Theorem 25-2 |
Closed-form formula for the maximum-likelihood estimate of the steady-state value of the innovation’s covariance matrix. |
Theorem 26-1 |
Differential equations for first-and second-order statistics of the continuous-time basic state-variable model. |
Theorem 26-2 |
Kalman-Bucy filter equations. |
Definition A-l |
Sufficient statistic defined. |
Theorem A-l |
Factorization theorem. |
Theorem A-2 |
A method for computing the unique maximum-likelihood estimator of θ that is associated with exponential families of distributions. |
Theorem A-3 |
Lehmann-Scheffe theorem. Provides a uniformly minimum-variance unbiased estimator of θ. |
Theorem A-4 |
Method for determining whether or not T(z) is complete as well as sufficient when p(zθ) is an m-parameter exponential family. |
Theorem A-5 |
Provides a uniformly minimum-variance unbiased estimator of vector θ. |
Definition B-l |
The kth-order cumulant for k random variables defined. |
Theorem B-l |
Symmetry conditions for third- and fourth-order cumulants. |
Definition B-3 |
The kth-order polyspectrum defined. |
Theorem B-2 |
Symmetry conditions for the bispectrum and trispectrum. |
Theorem B-3 |
Six cumulant properties. |
Theorem C-l |
The kth-order statistics of a linear time-invariant system (Bartlett-Brillinger-Rosenblatt theorem). |
Corollary C-l |
A cumulant formula for an ARMA(p, q) model. |
Corollary C-2 |
Relationship between the usual spectrum of a system’s output and a special polyspectrum (GM equation). |
Theorem C-2 |
Mean-squared optimality of a cumulant-based linear deconvolution filter. |