A number of two-person games have been shown to be PSPACE-complete. Indeed, the alternating quantifier characterization of Corollary 3.20 suggests that every problem in PSPACE may be viewed as a two-person game. For instance, the problem QBF may be viewed as a game played between two players where Figure 3.2 (a) The digraphs Hi and Ki. (b) An example of digraph H. In the following, we show a natural two-person game GEOGRAPHY to be PSPACE-complete. A game configuration of GEOGRAPHY is a directed graph All complete problems studied so far are candidates for intractable problems, but their intractability still depends on the separation of the classes NP, PSPACE, and PH from the class P. Are there natural problems that are provably intractable in the sense that they can be proved not belonging to P? In this section, we present a few problems that are complete for EXP and, hence, Our first EXP-complete problem is the bounded halting problem on deterministic machines with the time bound encoded in binary form. We note that in the above problem, if the time bound n is written in the unary form (as in the problem BHP), then the problem becomes polynomial-time solvable. Indeed, there is a simple translation of most P-complete problems1 to EXP-complete problems by more succinct encodings of the inputs. In the following, we demonstrate this idea on the famous P-complete problem, CIRCUIT VALUE PROBLEM (CVP). Let C be a Boolean circuit2 satisfying the following property: C has n gates numbered from 1 to n; we let C(i) denote the gate of C numbered i. There are four types of gates in circuit C: ZERO gates, ONE gates, AND gates, and OR gates. A ZERO (ONE) gate has no input and one output whose value is 0 (1, respectively). An AND (OR) gate has two inputs and one output whose value is the Boolean product (Boolean sum, respectively) of the two inputs. If the gate i is an AND or OR gate, then its two inputs are the outputs of two gates whose numbers are lower than i. Note that this circuit C does not have input gates and so it computes a unique Boolean value (the output of gate n). If the circuit is given explicitly, then its output value is computable in polynomial time. (In fact, it is P-complete; see Theorem 6.41). In the following, we consider the encoding of the circuit by a DTM. We say that a DTM M generates a circuit C of size n in time m if for all i, In Section 3.5, we have shown that a polynomially boundedtwo-person game is solvable in PSPACE and that some natural games, such as GEOGRAPHY, are PSPACE-complete. In the following, we consider a game that is not polynomially bounded and show that it is complete for the class EXP. Informally, the BOOLEAN FORMULA GAME (BFG) is a two-person game played on a Boolean formula F. The variables of the formula F are partitioned into three subsets: X, Y, and {t}. The game begins with an initial assignment τ0 on variables in A player loses if the formula F becomes 0 after his/her move. We notice that a Boolean formula F of m variables has 2m different assignments for its variables and, hence, this game is not polynomially bounded. In fact, the game may last forever, with two players repeating the same assignments. It is easy to see, nevertheless, that these repeated moves can be identified and ignored as far as the winning strategy is concerned. In the following formal definition of the game BFG, we write In the above, we have demonstrated some complete problems for the class EXP. In addition to these problems, there are problems that are known to have even higher complexity, for instance, complete for the classes NEXP, EXPSPACE, and so on. In the following, we list a few of these complete problems and leave their proofs asexercises. First, using the technique of succinct encoding for the problem EXP-CVP, we can encode a Boolean formula of exponential size in a DTM and the corresponding satisfiability problem becomes NEXP-complete. We say a 3-CNF formula is of size (n,m) if it has n Boolean variables and m clauses. We say that a DTM M generates a 3-CNF formula F of size (n,m) in time t if for any In Theorem 3.27, we showed that the problem of determining the totality of a given regular expression (TRE) is PSPACE-complete. The idea of the proof is that regular expressions can be used to encode computation paths of a DTM in such a way that a computation path of length exponential in n can be encoded by a regular expression of length polynomial in n. We say a string is an extended regular expression if it is a regular expression with an additional intersection operation 3.1 We say set A is strong-NP reducible to set B ( 3.2 Prove that there exist sets A,B, such that A≤SNPTB but not A≤PTB. 3.3 In this exercise, we study the complexity class DP. A language A is in the class DP (D stands for difference) if there exist sets 3.4 In this exercise, we extend the class DP to the Boolean hierarchy of sets between P and 3.5 An integer expression E is defined like a regular expression. It contains integer constants and the 3.6 The problem INTEGER EXPRESSION EQUIVALENCE (IEE) asks, for two given integer expressions 3.7 In the following, each problem is formulated to be a minimax function f. Prove that the corresponding decision problem of determining whether 3.8 Let CFL denote the class of context-free languages, and let LOGCFL be the class of sets that are reducible to the class CFL under the logarithmic-space reductions. 3.9 The transitive closure of a relation R is the set 3.10 The problem DETERMINISTIC FINITE AUTOMATA INTERSECTION (DFA-INT) asks, for a given sequence of deterministic finite automata 3.11 The problem MINIMAL NONDETERMINISTIC FINITE AUTOMATON (MIN-NFA) asks, for a given deterministic finite automaton M and an integer n, whether there exists an equivalent nondeterministic finite automaton that has at most n states. Prove that the problem MIN-NFA is PSPACE-complete. 3.12 Define formally the set GQBF of game configurations and the relations R0 and R1 for the game QBF. 3.13 Prove that it is a polynomially bounded game. Prove that the game GEOGRAPHY played on undirected graphs is solvable in polynomial time. 3.14 The game HEX played between two players 0 and 1 can be defined as follows: The game is played on a graph 3.15 Give a proof for Corollary 3.20 without using the notion of ATMs (instead, using the idea of the proof of Theorem 3.18 directly). 3.16 Verify that the size of the machine MC of Theorem 3.31 is bounded by 3.17 Consider the following variation of the game BFG: Prove that this version of the game BFG is also EXP-complete. 3.18 Prove Theorem 3.33. 3.19 Prove Theorem 3.34. 3.20 The problem ORACLE-SAT is defined as follows: Let G be a Boolean formula over five sets of variables The polynomial-time hierarchy was first introduced by Stockmeyer and Meyer (1973) as a polynomial-time analog of the arithmetic Hierarchy (Rogers, 1967). Stockmeyer (1977) and Wrathall (1977) contain complete sets SATk and the alternating quantifier characterizations. Stockmeyer (1977) also contains the The notion of strong-NP reducibility was introduced by Long (1982). A related strong-NP many-one reducibility was first used by Adleman and Manders (1977). The class DP and the corresponding DP-complete problems were studied in Papadimitriou and Yannakakis (1984) and Papadimitriou and Wolfe (1987). The Boolean hierarchy has been studied by a number of people. A comprehensive study was presented in Cai et al. (1988, 1989). The Theorem 3.28
Proof
![]() and
and ![]() . Without loss of generality, we may assume that a given QBF F has alternating quantifiers in its normal form:
. Without loss of generality, we may assume that a given QBF F has alternating quantifiers in its normal form:![]()
![]() if m is odd,
if m is odd, ![]() if m is even, and F1 is an unquantified Boolean formula over variables
if m is even, and F1 is an unquantified Boolean formula over variables ![]() . For any Boolean formula not of this form, we can insert a quantifier over a dummy variable between any two consecutive quantifiers of the same type to convert it to an equivalent formula of this form. On such a formula F, player
. For any Boolean formula not of this form, we can insert a quantifier over a dummy variable between any two consecutive quantifiers of the same type to convert it to an equivalent formula of this form. On such a formula F, player ![]() tries to prove that F is true and player
tries to prove that F is true and player ![]() works as an adversary trying to prove that F is false (see Exercise 3.12). When the problem QBF is presented as a game, the notion of the player
works as an adversary trying to prove that F is false (see Exercise 3.12). When the problem QBF is presented as a game, the notion of the player ![]() having a winning strategy is equivalent to the notion of F being true. Thus, the game QBF is PSPACE-complete.
having a winning strategy is equivalent to the notion of F being true. Thus, the game QBF is PSPACE-complete.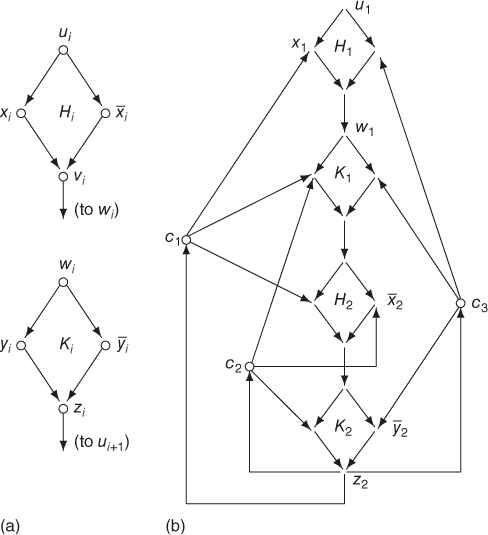
![]() with a starting node
with a starting node ![]() explicitly marked. There is a move from
explicitly marked. There is a move from ![]() to
to ![]() (i.e.,
(i.e., ![]() ) if H2 is the subgraph of H1 with the node v1 removed, and
) if H2 is the subgraph of H1 with the node v1 removed, and ![]() is an edge of H1. In other words, the players, starting with an initial graph H and a starting node v, take turns to visit one of the unvisited neighbors of the current node until one of the players reaches a node of which all the neighbors have been visited.
is an edge of H1. In other words, the players, starting with an initial graph H and a starting node v, take turns to visit one of the unvisited neighbors of the current node until one of the players reaches a node of which all the neighbors have been visited.GEOGRAPHY: Given a digraph H with a marked node v, determine whether the next player has a winning strategy.
Theorem 3.29
Proof
3.6 EXP-Complete Problems
EXPONENTIAL-TIME BOUNDED HALTING PROBLEM (EXP-BHP): Given a DTM M, a string x, and an integer n > 0, written in the binary form, determine whether M(x) halts in n moves.
Proposition 3.30
Proof
![]() , M(i) outputs a triple
, M(i) outputs a triple ![]() in m moves, with
in m moves, with ![]() and
and ![]() if b ≤ 1, such that
if b ≤ 1, such that
![]() ;
;![]() ;
;![]() ;
;![]() .
.EXPONENTIAL-SIZE CIRCUIT VALUE PROBLEM (EXP-CVP): Given a DTM M; an integer t > 0, written in the unary form 0t; and an integer s > 0, written in the binary form, such that M generates a circuit C of size s in time t, determine whether circuit C outputs 1.
Theorem 3.31
Proof
![]() such that F evaluates to 1 under τ0. The two players 0 and 1 take turns to change the assignment to variables, subject to the following rules:
such that F evaluates to 1 under τ0. The two players 0 and 1 take turns to change the assignment to variables, subject to the following rules:
![]() .
.![]() .
.![]() to denote a Boolean function with its variables partitioned into three sets A, B, and C. Now we define, following the notation of the last section,
to denote a Boolean function with its variables partitioned into three sets A, B, and C. Now we define, following the notation of the last section, ![]() , where
, where
BOOLEAN FORMULA GAME (BFG): Given a Boolean formula
![]() and a truth assignment
and a truth assignment ![]() such that
such that ![]() , determine whether the player 0 has a winning strategy on the game configuration
, determine whether the player 0 has a winning strategy on the game configuration ![]() .
.Theorem 3.32
Proof
![]() , M(j) outputs in t moves a 6-tuple
, M(j) outputs in t moves a 6-tuple ![]() , with
, with ![]() and
and ![]() , such that (i) the three variables occurring in clause Cj are
, such that (i) the three variables occurring in clause Cj are ![]() and (ii) for each
and (ii) for each ![]() ,
, ![]() occurs in Cj positively if and only if
occurs in Cj positively if and only if ![]() .
.EXP-SAT: Given a DTM M, integers n,m written in the binary form, and an integer t in unary form, such that M generates a 3-CNF formula F of size (n,m) in time t, determine whether F is satisfiable.
Theorem 3.33
![]() . For any two languages A and B,
. For any two languages A and B, ![]() simply denotes the set intersection of A and B. The following result indicates that even more succinct representations of a computation path of a DTM can be achieved by extended regular expressions.
simply denotes the set intersection of A and B. The following result indicates that even more succinct representations of a computation path of a DTM can be achieved by extended regular expressions.TOTALITY OF EXTENDED REGULAR EXPRESSION (TERE): Given an extended regular expression R over set Σ, determine whether
![]() .
.Theorem 3.34
Exercises
![]() ) if there is a polynomial-time oracle NTM M such that for each x, at least one computation path of
) if there is a polynomial-time oracle NTM M such that for each x, at least one computation path of ![]() halts in an accepting state, and all computation paths of
halts in an accepting state, and all computation paths of ![]() halting in an accepting state output value 1 if
halting in an accepting state output value 1 if ![]() , and all such paths output value 0 if
, and all such paths output value 0 if ![]() .
.
![]() is indeed a reducibility (i.e., it satisfies the transitivity property).
is indeed a reducibility (i.e., it satisfies the transitivity property).![]() if and only if [
if and only if [![]() and
and ![]() ] if and only if
] if and only if ![]() .
.![]() and
and ![]() imply
imply ![]() .
.![]() denote the class NPA and, for k ≥ 1, let
denote the class NPA and, for k ≥ 1, let ![]() denote the class
denote the class ![]() . Prove that, for k ≥ 1, if A is
. Prove that, for k ≥ 1, if A is ![]() -complete for the class
-complete for the class ![]() , then
, then ![]() .
.![]() and
and ![]() such that
such that ![]() .
.
![]() -reducibility.
-reducibility.![]() whether it is true that G does not have a Hamiltonian circuit but every graph G′ obtained from G by adding a new edge has a Hamiltonian circuit. Prove that CRITICAL HC is DP-complete.
whether it is true that G does not have a Hamiltonian circuit but every graph G′ obtained from G by adding a new edge has a Hamiltonian circuit. Prove that CRITICAL HC is DP-complete.![]() . For each n ≥ 0, define DPn as follows:
. For each n ≥ 0, define DPn as follows: ![]() ,
, ![]() if n is even, and
if n is even, and ![]() if n is odd. Then, define
if n is odd. Then, define ![]() .
.
![]() . We say set A is polynomial-time bounded truth-table reducible to set B, written
. We say set A is polynomial-time bounded truth-table reducible to set B, written ![]() , if
, if ![]() via a reduction function f and a set
via a reduction function f and a set ![]() such that, for any x,
such that, for any x, ![]() for some constant m ≥ 1. Show that a set A is in BH if and only if A is the union of a finite number of sets in DP if and only if
for some constant m ≥ 1. Show that a set A is in BH if and only if A is the union of a finite number of sets in DP if and only if ![]() for some
for some ![]() .
.![]() of graph G (the minimum number of colors necessary to color graph G) is odd and is between 3k and 4k. Prove that for each odd k, GCOLORk is DPk-complete.
of graph G (the minimum number of colors necessary to color graph G) is odd and is between 3k and 4k. Prove that for each odd k, GCOLORk is DPk-complete.![]() for each n ≥ 0) unless the polynomial-time hierarchy collapses.
for each n ≥ 0) unless the polynomial-time hierarchy collapses.![]() and
and ![]() operations. Each integer expression E represents a set L(E) of integers:
operations. Each integer expression E represents a set L(E) of integers: ![]() ,
, ![]() , and
, and ![]() .
.![]() , whether
, whether ![]() . Prove that IEE is
. Prove that IEE is ![]() -complete. The problem GRAPH CONSISTENCY (GC) asks, for two given sets A and B of graphs, whether there exists a graph G such that each graph
-complete. The problem GRAPH CONSISTENCY (GC) asks, for two given sets A and B of graphs, whether there exists a graph G such that each graph ![]() is isomorphic to a subgraph of G and each graph
is isomorphic to a subgraph of G and each graph ![]() is not isomorphic to any subgraph of G. Prove that the problem GC is
is not isomorphic to any subgraph of G. Prove that the problem GC is ![]() -complete.
-complete.![]() for some given graph G and constant K is
for some given graph G and constant K is ![]() -complete. In the following, we write Fn,m to mean the set of all functions
-complete. In the following, we write Fn,m to mean the set of all functions ![]() .
.
![]() with its vertices V partitioned into subsets Vi,j, for
with its vertices V partitioned into subsets Vi,j, for ![]() ,
, ![]() , find
, find ![]() is a clique in
is a clique in ![]() , where Gt is the induced subgraph of G on the vertex set
, where Gt is the induced subgraph of G on the vertex set ![]() .
.![]() ,
, ![]() , find
, find ![]() has a circuit on
has a circuit on ![]() , where Gt is defined as in (a) above.
, where Gt is defined as in (a) above.![]() ,
, ![]() , and a set S of three-element subsets of
, and a set S of three-element subsets of ![]() , find
, find ![]() is a matching in
is a matching in ![]() , where W(t) means the set
, where W(t) means the set ![]() .
.![]() and a subset E′ of E, find
and a subset E′ of E, find ![]() has a circuit on
has a circuit on ![]() , where GD is the subgraph of G with vertex set V and edge set
, where GD is the subgraph of G with vertex set V and edge set ![]() .
.
![]() .
.![]() .
.![]() there exists a sequence of strings
there exists a sequence of strings ![]() , such that
, such that ![]() for all i,
for all i, ![]() .
.
![]() with the property
with the property ![]() ,
, ![]() .
.![]() with the property
with the property ![]() , such that R∗ is PSPACE-complete.
, such that R∗ is PSPACE-complete.![]() over a common alphabet Σ, whether there exists a string
over a common alphabet Σ, whether there exists a string ![]() that is accepted by each Mi,
that is accepted by each Mi, ![]() . Prove that the problem DFA-INT is PSPACE-complete.
. Prove that the problem DFA-INT is PSPACE-complete.![]() with four explicitly marked nodes s0, t0, s1, and t1. The goal of the game for player 0 is to find a path from s0 to t0 and for player 1 is to find a path from s1 to t1 by player 1. At the beginning, all but the four special nodes are uncolored, and the four special nodes are colored by
with four explicitly marked nodes s0, t0, s1, and t1. The goal of the game for player 0 is to find a path from s0 to t0 and for player 1 is to find a path from s1 to t1 by player 1. At the beginning, all but the four special nodes are uncolored, and the four special nodes are colored by ![]() and
and ![]() . A legal move of player 0 (or player 1) is to mark any uncolored node with the color 0 (or color 1, respectively). The game ends when there is a path from s0 to t0 all colored with 0 (and player 0 wins) or when there is a path from s1 to t1 all colored with 1 (and player 1 wins).
. A legal move of player 0 (or player 1) is to mark any uncolored node with the color 0 (or color 1, respectively). The game ends when there is a path from s0 to t0 all colored with 0 (and player 0 wins) or when there is a path from s1 to t1 all colored with 1 (and player 1 wins).
![]() of game configurations and the relations R0 and R1. Prove that HEX is a polynomially bounded game.
of game configurations and the relations R0 and R1. Prove that HEX is a polynomially bounded game.![]() for some polynomial p.
for some polynomial p.
![]() , Y, and Z, where
, Y, and Z, where ![]() for
for ![]() , and
, and ![]() . Determine whether it is true that there exists a Boolean function
. Determine whether it is true that there exists a Boolean function ![]() such that for all assignments
such that for all assignments ![]() , G is satisfied by π and τ, where
, G is satisfied by π and τ, where ![]() is defined by
is defined by ![]() . (If
. (If ![]() , then we write
, then we write ![]() to denote the string of n bits:
to denote the string of n bits: ![]() .) Prove that ORACLE-SAT is
.) Prove that ORACLE-SAT is ![]() -complete for NEXP.
-complete for NEXP.Historical Notes
![]() -complete problem IEE (Exercise 3.5). The
-complete problem IEE (Exercise 3.5). The ![]() -complete problem GRN is from Ko and Lin (1995a). ATMs are first defined in Chandra et al. (1981). The simulations between ATMs, DTMs, and NTMs are proven there. The alternating quantifier characterization of PSPACE and the PSPACE-complete problems QBF are from Stockmeyer and Meyer (1973), and the PSPACE-completeness of TRE is from Meyer and Stockmeyer (1972). The first natural PSPACE-complete two-person game is HEX (Exercise 3.14), proved in Even and Tarjan (1976). Schaefer (1978b) contains many other PSPACE-complete games, including the game GEOGRAPHY. The idea of using TMs to encode objects of exponential size has been used in many applications; see, for instance, Ko (1992) for the EXP-complete problem EXP-CVP. The game BFG (Theorem 3.32 and Exercise 3.17) is from Stockmeyer and Chandra (1979). The EXPSPACE-complete problem TERE is from Hunt (1973).
-complete problem GRN is from Ko and Lin (1995a). ATMs are first defined in Chandra et al. (1981). The simulations between ATMs, DTMs, and NTMs are proven there. The alternating quantifier characterization of PSPACE and the PSPACE-complete problems QBF are from Stockmeyer and Meyer (1973), and the PSPACE-completeness of TRE is from Meyer and Stockmeyer (1972). The first natural PSPACE-complete two-person game is HEX (Exercise 3.14), proved in Even and Tarjan (1976). Schaefer (1978b) contains many other PSPACE-complete games, including the game GEOGRAPHY. The idea of using TMs to encode objects of exponential size has been used in many applications; see, for instance, Ko (1992) for the EXP-complete problem EXP-CVP. The game BFG (Theorem 3.32 and Exercise 3.17) is from Stockmeyer and Chandra (1979). The EXPSPACE-complete problem TERE is from Hunt (1973).![]() -complete problem GC (Exercise 3.6) is from Ko and Tzeng (1991). The
-complete problem GC (Exercise 3.6) is from Ko and Tzeng (1991). The ![]() -complete problems in Exercise 3.7 are from Ko and Lin (1995a). The class LOGCFL has been studied in connection with parallel complexity. Exercise 3.8(a) is from Ruzzo (1980) and Exercise 3.8(b) is from Sudborough (1978). The complexity of transitive closure was studied in Book and Wrathall (1982) and Ko (1985a). The DFA Intersection problem is from Kozen (1977) and the minimal NFA problem is from Jiang and Ravikumar (1993).
-complete problems in Exercise 3.7 are from Ko and Lin (1995a). The class LOGCFL has been studied in connection with parallel complexity. Exercise 3.8(a) is from Ruzzo (1980) and Exercise 3.8(b) is from Sudborough (1978). The complexity of transitive closure was studied in Book and Wrathall (1982) and Ko (1985a). The DFA Intersection problem is from Kozen (1977) and the minimal NFA problem is from Jiang and Ravikumar (1993).
