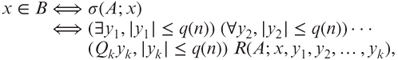In this section, we prove that The above proof actually gives a stronger result. Let MAJ be the following operator: We have seen in the last two sections that the class In this section, we investigate the relativized relations between these counting complexity classes and the polynomial-time hierarchy. We prove that in the relativized form, the complexity classes We first show how to translate a relativized separation problem involving the polynomial-time hierarchy into a lower bound problem about constant-depth circuits. Recall from Chapter 3 a set B in where Qk is In Corollary 6.38, it has been proved that any circuit of depth k that computes the parity of n variables must have size The relativized counting complexity classes The above theorem can actually be improved so that for a random oracle A, In this section, we apply the lower bound results on constant-depth circuits to separate the polynomial-time hierarchy by oracles. Let Let the function computed by The above proof technique is not only strong enough to separate the polynomial-time hierarchy by oracles, but it also can be applied to collapse the polynomial-time hierarchy to any finite level. These results suggest that the relativized results on the polynomial-time hierarchy do not bear much relation to the nonrelativized questions, though the proof technique of using lower bound results on constant-depth circuits is itself interesting. Finally, we remark that it is unknown whether the relativized polynomial-time hierarchy is a properly infinite hierarchy relative to a random oracle. In Theorem 9.35, we applied the stronger lower bound result on parity circuits to show that 9.1 Let 9.2 A matching in a bipartite graph G is a set of edges which do not share common vertices. The problem GENERAL MATCHING (GM) is to count the number of matchings of a given bipartite graph. Prove that the problem GM is 9.3 Prove that the problem #SAT remains 9.4 Let LE be the problem of counting the number of linear extensions of a given partial ordering on a given set A; that is, for a given set 9.5 For a set 9.6 In the proof of Lemma 9.23, we used the second Swapping Lemma to prove (9.1). This seems unnecessary: By Lemma 9.22(a), the error probability of (9.2) can be reduced to 9.7 Let n ≥ 1. Identify the set 9.8 Let PRIMESAT = 9.9 In this exercise, we prove a straight-line program characterization of the class #P. A straight-line arithmetic program (or, simply, program) is a finite sequence Such a program 9.10 Let 9.11 A fully probabilistic polynomial-time approximation scheme for a counting function 9.12 Prove that the class 9.13 Let FewP denote the class of languages L that are accepted by polynomial-time NTMs that have at most a polynomial number of accepting computation paths for any 9.14 Prove that there exists an oracle A such that 9.15 Prove Theorem 9.34. That is, do a more careful analysis of the proofs of Theorems 6.46 and 6.47 to get an exponential lower bound for the size of any depth-d circuit 9.16 Prove Theorem 9.37. In particular, prove that 9.17 9.18 In this exercise, we consider the low and high hierarchies in NP. For each k ≥ 0, let 9.19 We consider the relativized low and high hierarchies in NP. For any set X, we let The class The reduction from the relativization problem to the lower bound problem for constant-depth circuits was given in Furst et al. (1984) and Sipser (1983a). They also proved that the parity circuit complexity is super-polynomial. The separation of PSPACE from PH by oracles and the separation of PH into a properly infinite hierarchy by oracles are given in Yao (1985) and Hastad (1986a, 1986b). The collapsing of PH to any finite levels and the separation of PSPACE from a collapsed PH by oracles was proved in Ko (1989a). Theorem 9.35, showing that random oracles separate PSPACE from PH, was first proven by Cai (1986). Our simplified version is from Babai (1987). The low and high hierarchies were first introduced by Schöning (1983). Exercise 9.18 is from there. The relativized separation and collapsing of the low and high hierarchies (Exercise 9.19) was proved by Ko (1991b) and Sheu and Long (1992). Ko (1989b) contains a survey of the proof techniques that use the lower bound results for circuits to construct oracles.Corollary 9.27
Proof
9.4
![]() and the Polynomial-Time Hierarchy
and the Polynomial-Time Hierarchy![]() . From Theorem 9.26, we only need to show that
. From Theorem 9.26, we only need to show that ![]() . The main idea is that the number of accepting computations of an NTM can be amplified without changing its parity. Recall that
. The main idea is that the number of accepting computations of an NTM can be amplified without changing its parity. Recall that ![]() denotes the number of accepting computations of an NTM M on input x.
denotes the number of accepting computations of an NTM M on input x.Lemma 9.28
Proof
Theorem 9.29
Proof
Corollary 9.30
![]() if for all x,
if for all x, ![]() for some polynomial p. Also define, for a class
for some polynomial p. Also define, for a class ![]() of sets, MAJ
of sets, MAJ![]() .
.Corollary 9.31
Proof
9.5 Circuit Complexity and Relativized
![]() and
and ![]()
![]() is hard for PH under the polynomial-time randomized reduction and the class
is hard for PH under the polynomial-time randomized reduction and the class ![]() is hard for PH under the polynomial-time Turing reduction. These results imply that if
is hard for PH under the polynomial-time Turing reduction. These results imply that if ![]() or
or ![]() is actually contained in PH, then PH collapses into a finite hierarchy. On the other hand, if either
is actually contained in PH, then PH collapses into a finite hierarchy. On the other hand, if either ![]() or
or ![]() is provably not contained in PH, then
is provably not contained in PH, then ![]() , because
, because ![]() . Therefore, it appears difficult to determine the precise relations between
. Therefore, it appears difficult to determine the precise relations between![]() ,
, ![]() , and the polynomial-time hierarchy.
, and the polynomial-time hierarchy.![]() and
and ![]() are not contained in PH. The proof technique is particularly interesting, as it demonstrates a simple relation between the relativized separation results on classes in PH and the lower bound results on circuit complexity. Using the lower bound results on constant-depth circuits of Section 6.6, we are able to separate the relativized counting complexity classes from the polynomial-time hierarchy and, moreover, to separate the polynomial-time hierarchy into a properly infinite hierarchy by oracles.
are not contained in PH. The proof technique is particularly interesting, as it demonstrates a simple relation between the relativized separation results on classes in PH and the lower bound results on circuit complexity. Using the lower bound results on constant-depth circuits of Section 6.6, we are able to separate the relativized counting complexity classes from the polynomial-time hierarchy and, moreover, to separate the polynomial-time hierarchy into a properly infinite hierarchy by oracles.![]() can be characterized by a
can be characterized by a ![]() -predicate
-predicate ![]() : for each x of length n,
: for each x of length n,![]() if k is odd and is
if k is odd and is ![]() if k is even and R is a polynomial-time computable predicate relative to any oracle A. Also recall from Section 6.6 the notion of constant-depth levelable Boolean circuits. Such a circuit has alternating AND and OR gates at each level. Each gate of the circuit has an unlimited fan-in, and its input nodes can take an input value as it is or take its negated value. In the following, by a circuit we mean a constant-depth levelable circuit. We label each input node of a circuit C by a string z or its negation
if k is even and R is a polynomial-time computable predicate relative to any oracle A. Also recall from Section 6.6 the notion of constant-depth levelable Boolean circuits. Such a circuit has alternating AND and OR gates at each level. Each gate of the circuit has an unlimited fan-in, and its input nodes can take an input value as it is or take its negated value. In the following, by a circuit we mean a constant-depth levelable circuit. We label each input node of a circuit C by a string z or its negation ![]() . These labels are called variables of C. We say that a variable z in C is assigned with a Boolean value b to mean that each input node with the label z takes the input value b and each input node with the label
. These labels are called variables of C. We say that a variable z in C is assigned with a Boolean value b to mean that each input node with the label z takes the input value b and each input node with the label ![]() takes the input value
takes the input value ![]() .
.Lemma 9.32
Proof
![]() for some constant c > 0. We apply this lower bound on parity circuits to show that
for some constant c > 0. We apply this lower bound on parity circuits to show that ![]() is not in PHA for some oracle A.
is not in PHA for some oracle A.![]() and
and ![]() can be defined naturally. Namely, a set B is in
can be defined naturally. Namely, a set B is in ![]() if there exist a set
if there exist a set ![]() and a polynomial q such that for each x,
and a polynomial q such that for each x, ![]() if and only if there exists an odd number of y of length
if and only if there exists an odd number of y of length ![]() satisfying
satisfying ![]() . That is,
. That is, ![]() . Similarly, a function f is in
. Similarly, a function f is in ![]() if there exist a set
if there exist a set ![]() and a polynomial q such that for each x, f(x) is the number of strings y of length
and a polynomial q such that for each x, f(x) is the number of strings y of length ![]() such that
such that ![]() .
.Theorem 9.33
Proof
![]() . To prove this result, we recall the result of Theorem 6.47, in which it was proved that the parity function cannot be
. To prove this result, we recall the result of Theorem 6.47, in which it was proved that the parity function cannot be ![]() -approximated by polynomial-size constant-depth circuits. In fact, Theorem 6.47 can be improved to the following form (see Exercise 9.15).
-approximated by polynomial-size constant-depth circuits. In fact, Theorem 6.47 can be improved to the following form (see Exercise 9.15).Theorem 9.34
Theorem 9.35
Proof
9.6 Relativized Polynomial-Time Hierarchy
![]() be the depth-d levelable circuit that has the following structure:
be the depth-d levelable circuit that has the following structure:
![]() has a top OR gate.
has a top OR gate.![]() has exactly nd variables, each variable occurring exactly once in a leaf in the positive form.
has exactly nd variables, each variable occurring exactly once in a leaf in the positive form.![]() be
be ![]() . From Exercise 6.20, we know that for any ℓ and sufficiently large n, a depth-d circuit D with fan-in
. From Exercise 6.20, we know that for any ℓ and sufficiently large n, a depth-d circuit D with fan-in ![]() and bottom fan-in
and bottom fan-in ![]() cannot compute
cannot compute ![]() (because such a circuit has size bounded by
(because such a circuit has size bounded by ![]() for large n, where c is the constant given in Exercise 6.20). We apply this lower bound result to separate the relativized polynomial-time hierarchy.
for large n, where c is the constant given in Exercise 6.20). We apply this lower bound result to separate the relativized polynomial-time hierarchy.Theorem 9.36
Proof
Theorem 9.37
Proof
![]() is not contained in PHA relative to a random oracle A. Namely, the stronger lower bound implies that no circuit of a constant depth d and size
is not contained in PHA relative to a random oracle A. Namely, the stronger lower bound implies that no circuit of a constant depth d and size ![]() for any polynomial p can approximate the parity function correct on more than
for any polynomial p can approximate the parity function correct on more than ![]() inputs. Similarly, if we could show a stronger lower bound result on depth-
inputs. Similarly, if we could show a stronger lower bound result on depth-![]() Circuits that
Circuits that ![]() -approximate
-approximate ![]() , then it follows that the polynomial-time hierarchy is properly infinite relative to a random oracle. Note, however, that the symmetry property of the parity function is critical to the proof of Theorem 9.34. Without the symmetry property, the lower bound on the approximation circuits for function
, then it follows that the polynomial-time hierarchy is properly infinite relative to a random oracle. Note, however, that the symmetry property of the parity function is critical to the proof of Theorem 9.34. Without the symmetry property, the lower bound on the approximation circuits for function ![]() appears more difficult.
appears more difficult.Exercises
![]() be the problem of counting the number of Hamiltonian circuits of a given graph G and #SS be the problem of counting the number of ways to select a sublist, from a given list of integers, so that the sublist sums to a given integer K > 0. Prove that the problems
be the problem of counting the number of Hamiltonian circuits of a given graph G and #SS be the problem of counting the number of ways to select a sublist, from a given list of integers, so that the sublist sums to a given integer K > 0. Prove that the problems ![]() and #SS are
and #SS are ![]() -complete.
-complete.![]() -complete.
-complete.![]() -complete even if we restrict the input formulas to be of the form 2-CNF and be monotone. (A CNF Boolean formula is monotone if all literals in each clause appear in the nonnegated form.)
-complete even if we restrict the input formulas to be of the form 2-CNF and be monotone. (A CNF Boolean formula is monotone if all literals in each clause appear in the nonnegated form.)![]() and a set
and a set ![]() of ordered pairs of elements in A, find the number of total ordering
of ordered pairs of elements in A, find the number of total ordering ![]() over A such that for each pair
over A such that for each pair ![]() in B,
in B, ![]() . Prove that the problem LE is
. Prove that the problem LE is ![]() -complete. [Hint: Similar to the problem PERM, first show that for each fixed but sufficiently large prime number p, each Boolean formula F can be reduced to a partial ordering PF on a set A such that #SAT
-complete. [Hint: Similar to the problem PERM, first show that for each fixed but sufficiently large prime number p, each Boolean formula F can be reduced to a partial ordering PF on a set A such that #SAT![]() is reducible to the number of linear extensions of PF.]
is reducible to the number of linear extensions of PF.]![]() and a subset
and a subset ![]() , a pair (T,a), with
, a pair (T,a), with ![]() and
and ![]() , is said to be consistent with B if [a = 0 and
, is said to be consistent with B if [a = 0 and ![]() ] or [a = 1 and
] or [a = 1 and ![]() ].
].
![]() and a set
and a set ![]() , with
, with ![]() and each
and each ![]() for each
for each ![]() , find the number of subsets
, find the number of subsets ![]() such that each pair
such that each pair ![]() ,
, ![]() , is consistent with B.
, is consistent with B.![]() is an additional input parameter.
is an additional input parameter.![]() , and then the inequality (9.1), with
, and then the inequality (9.1), with ![]() , follows immediately. Discuss what was wrong with this simpler argument.
, follows immediately. Discuss what was wrong with this simpler argument.![]() with the vector space
with the vector space ![]() of all n-dimensional vectors over the field
of all n-dimensional vectors over the field ![]() . Then, for any two strings
. Then, for any two strings ![]() , their inner product is
, their inner product is ![]() , where ui denotes the ith bit of u and
, where ui denotes the ith bit of u and ![]() denotes the exclusive-or, or the odd parity, operation.
denotes the exclusive-or, or the odd parity, operation.
![]() ,
, ![]() , define
, define ![]() , for
, for ![]() . Prove that
. Prove that ![]() and
and ![]() .
.![]() . For any random strings w1,
. For any random strings w1, ![]() ,
, ![]() , define
, define![]() ,
, ![]() ,
, ![]() . Prove that
. Prove that ![]() .
.![]() SAT: the number of truth assignments t that satisfies F is a prime number}. Prove that SAT
SAT: the number of truth assignments t that satisfies F is a prime number}. Prove that SAT![]() (PRIMESAT).
(PRIMESAT).![]() of instructions such that each pk,
of instructions such that each pk, ![]() , is of one of the following forms:
, is of one of the following forms:
![]() or
or ![]() for some
for some ![]() ,
,![]() for some
for some ![]() ,
,![]() for some
for some ![]() , or
, or![]() or
or ![]() for some
for some ![]() . (
. (![]() means the polynomial obtained from pj by substituting 0 for the variable xi.)
means the polynomial obtained from pj by substituting 0 for the variable xi.)![]() is said to compute the polynomial pt; we denote it by
is said to compute the polynomial pt; we denote it by ![]() . A family of programs
. A family of programs ![]() is a uniform family if each
is a uniform family if each ![]() has at most k variables
has at most k variables ![]() and if there is a polynomial-time DTM transducer that prints the instructions of program Qk from input 1k. Prove that a counting function
and if there is a polynomial-time DTM transducer that prints the instructions of program Qk from input 1k. Prove that a counting function ![]() is in #P if and only if there is a uniform family of programs Qk such that, for all
is in #P if and only if there is a uniform family of programs Qk such that, for all ![]() of length n,
of length n, ![]() , where wj denotes the jth bit of w.
, where wj denotes the jth bit of w.![]() be two counting functions, and
be two counting functions, and ![]() an integer function. We say that function g approximates f with errors bounded by r(n) if for any
an integer function. We say that function g approximates f with errors bounded by r(n) if for any ![]() ,
,![]()
![]() denote the class of functions
denote the class of functions ![]() that are computable by a polynomial-time oracle DTM with respect to an oracle in
that are computable by a polynomial-time oracle DTM with respect to an oracle in ![]() . Prove that for any
. Prove that for any ![]() and any polynomial function r, there exists a function
and any polynomial function r, there exists a function ![]() such that g approximates f with errors bounded by r. In addition, the oracle DTM for g queries only the oracle for at most
such that g approximates f with errors bounded by r. In addition, the oracle DTM for g queries only the oracle for at most ![]() times.
times.![]() denote the class of functions
denote the class of functions ![]() that are computable by a polynomial-time oracle PTM with respect to an oracle in NP such that the error probability is bounded by 1/4. Prove that for any
that are computable by a polynomial-time oracle PTM with respect to an oracle in NP such that the error probability is bounded by 1/4. Prove that for any ![]() and any polynomial function r, there exists a function
and any polynomial function r, there exists a function ![]() such that g approximates f with errors bounded by r. In fact, the oraclemachine for g queries only the oracle for at most
such that g approximates f with errors bounded by r. In fact, the oraclemachine for g queries only the oracle for at most ![]() times.
times.![]() is a PTM that on inputs x and ε computes, in time polynomial in
is a PTM that on inputs x and ε computes, in time polynomial in ![]() and with probability 3/4, an approximate value to f(x) with errors bounded by ε.
and with probability 3/4, an approximate value to f(x) with errors bounded by ε.
![]() with
with ![]() is dense if each node has degree at least
is dense if each node has degree at least ![]() . A 0-1-matrix is called dense if it is the adjacency matrix of a dense bipartite graph. Prove that the problem PERM restricted to dense 0-1-matrices remains #P-complete.
. A 0-1-matrix is called dense if it is the adjacency matrix of a dense bipartite graph. Prove that the problem PERM restricted to dense 0-1-matrices remains #P-complete.![]() is closed under the Boolean operations union, intersection, and complementation.
is closed under the Boolean operations union, intersection, and complementation.![]() . Prove that the class
. Prove that the class ![]() .
.![]() and NPA are incomparable.
and NPA are incomparable.![]() -approximating the parity function pn.
-approximating the parity function pn.
![]() ; and
; and![]() . [Hint: Use Exercise 6.21.]
. [Hint: Use Exercise 6.21.]
![]() for all k ≥ 1.
for all k ≥ 1.![]() for all k ≥ 1.
for all k ≥ 1.![]() be the class of sets
be the class of sets ![]() such that
such that ![]() and
and ![]() be the class of sets
be the class of sets ![]() such that
such that ![]() .
.
![]() and
and ![]() for all k ≥ 0.
for all k ≥ 0.![]() and
and ![]() equals the class of sets A that are
equals the class of sets A that are ![]() -complete for NP.
-complete for NP.![]() , then
, then ![]() .
.![]() , then
, then ![]() .
.![]() denote the class of sets
denote the class of sets ![]() such that
such that ![]() and let
and let ![]() denote the class of sets
denote the class of sets ![]() such that
such that ![]() . Note that Theorem 4.20(c) showed that there exists an oracle A such that
. Note that Theorem 4.20(c) showed that there exists an oracle A such that ![]() .
.
![]() and
and ![]() for all k ≥ 0.
for all k ≥ 0.![]()
![]()
![]() . Show that there exists an oracle Z such that UPZ is not contained in the low and high hierarchies relative to Z, that is,
. Show that there exists an oracle Z such that UPZ is not contained in the low and high hierarchies relative to Z, that is,
![]()
Historical Notes
![]() was first defined in Valiant (1979a, 1979b), in which the
was first defined in Valiant (1979a, 1979b), in which the ![]() -completeness of PERM and other counting problems associated with NP-complete problems are proven. The natural reductions among many NP-complete problems are known to preserve the number of solutions; see, for example, Simon (1975) and Berman and Hartmanis (1977). The
-completeness of PERM and other counting problems associated with NP-complete problems are proven. The natural reductions among many NP-complete problems are known to preserve the number of solutions; see, for example, Simon (1975) and Berman and Hartmanis (1977). The ![]() -completeness of the problem LE (Exercise 9.4) is proved by Brightwell and Winkler (1991). Exercise 9.5 is from Du and Ko (1987). The straight-line program characterization of #P (Exercise 9.9) is from Babai and Fortnow (1991). Papadimitirou and Zachos (1983) studied the class
-completeness of the problem LE (Exercise 9.4) is proved by Brightwell and Winkler (1991). Exercise 9.5 is from Du and Ko (1987). The straight-line program characterization of #P (Exercise 9.9) is from Babai and Fortnow (1991). Papadimitirou and Zachos (1983) studied the class ![]() and proved that
and proved that ![]() . Exercise 9.13 is from Cai and Hemachandra (1990). Theorem 9.24 was first proved by Valiant and Vazirani (1986), using a different probabilistic lemma (see Exercise 9.7). The use of the Isolation Lemma simplifies the proof; this was pointed out by Mulmuley et al. (1987). Lemma 9.23, Theorem 9.26, and the results of Section 9.4 are all from Toda (1991). Approximation to counting functions were studied by Stockmeyer (1985), Jerrum et al. (1986), Broder (1986), and Jerrum and Sinclair (1989). Exercises 9.10 and 9.11 are from these works.
. Exercise 9.13 is from Cai and Hemachandra (1990). Theorem 9.24 was first proved by Valiant and Vazirani (1986), using a different probabilistic lemma (see Exercise 9.7). The use of the Isolation Lemma simplifies the proof; this was pointed out by Mulmuley et al. (1987). Lemma 9.23, Theorem 9.26, and the results of Section 9.4 are all from Toda (1991). Approximation to counting functions were studied by Stockmeyer (1985), Jerrum et al. (1986), Broder (1986), and Jerrum and Sinclair (1989). Exercises 9.10 and 9.11 are from these works.