To establish a general lower bound for the randomized decision tree complexity of weakly symmetric functions, let us first show an inequality about weakly symmetric functions.
Lemma 5.38
Proof
Theorem 5.39
Proof
Next, we develop some tools for studying the lower bounds of random decision tree complexity.
Lemma 5.40
Proof
Lemma 5.41
Proof
Example 5.42
In general, the Yao–Karp conjecture states that for any nontrivial monotone graph property ![]() ,
, ![]() , where n is the number of vertices.
, where n is the number of vertices.
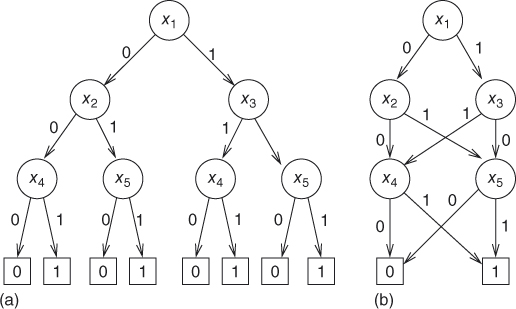
Figure 5.9 From a decision tree to a branching program.
5.9 Branching Programs
Consider a decision tree as shown in Figure 5.9(a). We see that some subtrees are identical. For such subtrees, we may use a single procedure to realize them. To exhibit this property explicitly, we may use an acyclic digraph instead of a tree to represent a decision process (see Figure 5.9(b)). Such a “decision graph” will be called a branching program. In general, a branching program of n variables is an acyclic digraph that includes a single source node and some sink nodes. Each nonsink node is labeled by a variable and has exactly two out-edges labeled by 0 and 1, and each sink node is labeled by either 0 or 1. Note that in a decision tree, each variable appears at most once in any path from the root to a leaf. However, in a branching program, each variable may appear more than once in a path from the source to a sink. This relaxation provides a possibility to make a branching program scrawny.
The two most important complexity measures of a branching program are length (or, depth) and width. A bounded-width branching program of width w and length r is a branching program consisting of r levels, each with at most w nodes. Each directed edge goes from a node on one level to a node on the next level. Sink nodes exist only in the bottom level. The size of a branching program is the number of nodes in the program.
At the expense of increasing the size by a factor of w, a width-bounded branching program may sometimes be modified to have the property that all nodes in the same level have the same label. For such a branching program, one can give an algebraic interpretation: With a little modification on the first level, each level k (![]() ) can be seen as an instruction to read the input value ti of a variable xi, where xi is the label of the nodes on this level, and then emit a mapping
) can be seen as an instruction to read the input value ti of a variable xi, where xi is the label of the nodes on this level, and then emit a mapping ![]() . The mappings emitted at all levels are composed and the Boolean function computed by the branching program has value 1 at the input assignment if and only if the composite mapping maps number 1 to a number in
. The mappings emitted at all levels are composed and the Boolean function computed by the branching program has value 1 at the input assignment if and only if the composite mapping maps number 1 to a number in ![]() , which corresponds to a sink labeled by 1 at the bottom level. The set of mappings from
, which corresponds to a sink labeled by 1 at the bottom level. The set of mappings from ![]() into itself forms a monoid M. Let X be the set of mapping that maps 1 to a number in
into itself forms a monoid M. Let X be the set of mapping that maps 1 to a number in ![]() corresponding to a sink labeled by 1 at the bottom level. Then we obtain a program over monoid M consisting of a sequence of instructions
corresponding to a sink labeled by 1 at the bottom level. Then we obtain a program over monoid M consisting of a sequence of instructions
together with a subset X of M, where each gk is a mapping from {0,1} to M and each ik indicates the variable ![]() at the level k. On input assignment
at the level k. On input assignment ![]() , the program obtains the value 1 if and only if
, the program obtains the value 1 if and only if
A permutation branching program is a program over a group, that is, the mapping emitted at each level is a permutation. A permutation branching program is given in Figure 5.10, which computes the parity function ![]() .
.
When the width is too small, the power of the permutation branching program is limited. The following is a simple example.
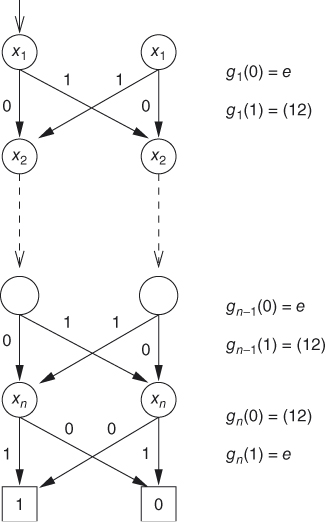
Figure 5.10 A permutation branching program  .
.
Example 5.43
Given a Boolean function, how do we design a branching program computing it? In the following, we study a method of constructing permutation branching programs. This method was first introduced by Barrington (1990).
Let σ be a permutation that is not the identity. We say a permutation branching program ![]() ,
, ![]() ,
, ![]() σ-computes a Boolean function f if
σ-computes a Boolean function f if
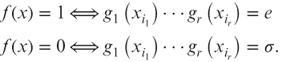
For example, the permutation branching program in Figure 5.10 (12)-computes parity function pn.
The main idea of Barrington's method is to build a branching program recursively by following the negation and disjunction operations in the formula. In fact, constructing a branching program computing a literal is easy and any Boolean function can be built up based on literals through the negation and disjunction operations because ![]() , that is, conjunction can be represented through negation and disjunction. Let us first prove some properties of a permutation branching program that σ-computes a Boolean function for some cyclic σ. (A permutation is cyclic if it is composed of a single cycle on all of its elements.)
, that is, conjunction can be represented through negation and disjunction. Let us first prove some properties of a permutation branching program that σ-computes a Boolean function for some cyclic σ. (A permutation is cyclic if it is composed of a single cycle on all of its elements.)
Lemma 5.44
Proof
Lemma 5.45
Proof
Lemma 5.46
Proof
The above lemmas suggest a recursive procedure to build up a permutation branching program computing a Boolean function. In order to guarantee that this procedure always works, we need to make sure that ![]() is cyclic.
is cyclic.
Lemma 5.47
Proof
Now, let us look at an example.
Example 5.48
Barrington's method is simple and elegant. However, the branching program obtained by his method is a special kind of branching program. So, it is not necessarily of the minimum length. In fact, the permutation branching programs usually require length longer than the general branching programs. For example, consider function ![]() . Clearly, a branching program of width 2 and length n could compute it. However, it requires length
. Clearly, a branching program of width 2 and length n could compute it. However, it requires length ![]() for any permutation branching program of a constant width w. To show this result, we first prove two combinatorial lemmas.
for any permutation branching program of a constant width w. To show this result, we first prove two combinatorial lemmas.
Lemma 5.49
Proof
Consider a sequence S of elements from ![]() . For
. For ![]() , let SI denote the subsequence of S consisting of all occurrences of elements in I.
, let SI denote the subsequence of S consisting of all occurrences of elements in I.
Lemma 5.50
Proof
Theorem 5.51
Proof
The above is an explicit lower bound for permutation branching programs. What can we say about the lower bound for general branching programs? By a counting argument, it is known that most Boolean functions have exponential lower bounds. However, the best known lower bound for an explicit function is only ![]() due to Neciporuk (1966).
due to Neciporuk (1966).
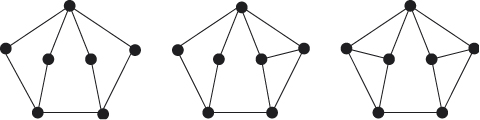
Figure 5.11 Three graphs H1, H2, and H3.
Exercises
5.1 Nonplanarity is a monotone increasing graph property. Characterize its minterms by using Kuratowski's theorem. (Kuratowski's theorem: A graph is not planar if and only if it has a subgraph isomorphic to ![]() or K5, that is, if the graph can be obtained from the complete bipartite graph
or K5, that is, if the graph can be obtained from the complete bipartite graph ![]() or the complete graph K5 by adding some vertices and some edges.)
or the complete graph K5 by adding some vertices and some edges.)
5.2 Prove that a graph property is monotone increasing if and only if there exists a family of graphs such that a graph has the property if and only if the graph contains a subgraph in the family.
5.3 Given a digraph ![]() , construct a bipartite graph
, construct a bipartite graph ![]() by setting
by setting ![]() and
and ![]() . For any bipartite graph property
. For any bipartite graph property ![]() , define
, define ![]() . Is
. Is ![]() a digraph property?
a digraph property?
5.4 Suppose ![]() and
and ![]() . For each bipartite graph
. For each bipartite graph ![]() , construct a digraph
, construct a digraph ![]() by setting
by setting ![]() . Define
. Define
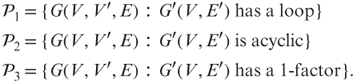
(A 1-factor is a union of vertex-disjoint cycles passing through all vertices.) For each ![]() , determine whether
, determine whether ![]() is a bipartite graph property.
is a bipartite graph property.
5.5 Prove that in a binary tree, the sum of distances from internal vertices to the closest leaves is less than the total number of edges in the binary tree.
5.6 Prove that ![]() ,
, ![]() , and
, and ![]() .
.
5.7 If x is the variable labeling the root of a decision tree that is of depth D(f) and computes function f, then ![]() and
and ![]() . If x is any variable of f, does the inequality still hold? Give a proof or show a counterexample.
. If x is any variable of f, does the inequality still hold? Give a proof or show a counterexample.
5.8 Prove that ![]() and
and ![]() , where y and z are two variables other than the variables in the parity function pn.
, where y and z are two variables other than the variables in the parity function pn.
5.9 Let ![]() . Find two ways to prove that
. Find two ways to prove that ![]() .
.
5.10 Let ![]() be a Boolean function with minterms of size at least n − 1. Suppose that for any variable xi, there exists a minterm not containing xi. Prove that f is elusive.
be a Boolean function with minterms of size at least n − 1. Suppose that for any variable xi, there exists a minterm not containing xi. Prove that f is elusive.
5.11 Let H be a graph with n vertices and ![]() the graph property consisting of all graphs isomorphic to H. Determine
the graph property consisting of all graphs isomorphic to H. Determine ![]() ,
, ![]() , and
, and ![]() .
.
5.12 Let H1 and H2 be two different graphs on the same set of n vertices. Let ![]() be the graph property consisting of all graphs isomorphic to either H1 or H2. Prove that
be the graph property consisting of all graphs isomorphic to either H1 or H2. Prove that ![]() is elusive.
is elusive.
5.13 Let H1, H2, and H3 be three graphs as shown in Figure 5.11. Let ![]() be the graph property consisting of all graphs isomorphic to H1, H2, or H3. Prove that
be the graph property consisting of all graphs isomorphic to H1, H2, or H3. Prove that ![]() is not elusive.
is not elusive.
5.14 Draw a decision tree for Example 5.2 with five players and a decision tree for Example 5.5 with four vertices.
5.15 A graph G of n vertices is a scorpion graph if it contains a vertex t of degree 1, a vertex b of degree n − 2, and a vertex a of degree 2 adjacent to t and b. Suppose that ![]() is the property of a graph being scorpion. Then
is the property of a graph being scorpion. Then ![]() .
.
5.16 Is the Boolean function t in Example 1.1 a graph property? Is it a digraph property? Explain each of your answers by either a proof or a disproof.
5.17 If all graphs satisfying nontrivial property ![]() form a matroid, then
form a matroid, then ![]() is elusive. (A collection
is elusive. (A collection ![]() of graphs on the same vertex set V is a matroid if the following two conditions hold: (1)
of graphs on the same vertex set V is a matroid if the following two conditions hold: (1) ![]() . (2) For any
. (2) For any ![]() and any edge e not in G, there exists an edge e′ in G such that
and any edge e not in G, there exists an edge e′ in G such that ![]() .)
.)
5.18 Prove that the following graph properties are elusive:
- The graph is acyclic.
- The graph is 2-connected.
- The graph is a spanning tree.
- The graph has at most k edges.
5.19 Let ![]() be the following property of graphs of order n: there exists an isolated star of n − 4 leaves. Prove that
be the following property of graphs of order n: there exists an isolated star of n − 4 leaves. Prove that ![]() is not elusive.
is not elusive.
5.20 Prove that the assumption condition in Theorem 5.6 is necessary.
5.21 Use the algebraic criterion to prove that Boolean function ![]() is elusive.
is elusive.
5.22 Prove that every nontrivial symmetric Boolean function is elusive.
5.23 Define ![]() if and only if
if and only if ![]() contains three consecutive 1's. Prove the following:
contains three consecutive 1's. Prove the following:
 is not elusive.
is not elusive.- For n ≡ 0 or 3
 ,
, 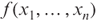 is elusive.
is elusive.
5.24Define ![]() . Prove that
. Prove that ![]() is in the ideal generated by
is in the ideal generated by ![]() ,
, ![]() in the polynomial ring.
in the polynomial ring.
5.25 Let f be a Boolean function. Function ![]() is called the Mobius transform of f. Prove that if
is called the Mobius transform of f. Prove that if ![]() , then
, then ![]() .
.
5.26 Show that ![]() implies
implies ![]() , where n is the number of variables. If we replace n by
, where n is the number of variables. If we replace n by ![]() , is the above relation still true?
, is the above relation still true?
5.27 Prove that if the number of truth assignments for Boolean function f is odd, then ![]() .
.
5.28 Prove or disprove that if ![]() is a non-elusive property of graphs of order n, then the number of graphs satisfying
is a non-elusive property of graphs of order n, then the number of graphs satisfying ![]() can be divided by four.
can be divided by four.
5.29 Let ![]() . Then the property of all graphs of order n which contains a complete subgraph of order r is elusive.
. Then the property of all graphs of order n which contains a complete subgraph of order r is elusive.
5.30 Let ![]() . Then the property of r-colorable graphs of order n is elusive.
. Then the property of r-colorable graphs of order n is elusive.
5.31 Let H be a given graph of order r and ![]() the property of graphs of order n containing a subgraph isomorphic toH. Prove that
the property of graphs of order n containing a subgraph isomorphic toH. Prove that ![]() .
.
5.32 Prove
where n is the number of vertices in Δ.
5.33 Let ![]() . Draw a geometric representation of Δf and compute
. Draw a geometric representation of Δf and compute ![]() .
.
5.34 Prove that the simple strategy is a winning strategy for proving the elusiveness of a monotone increasing Boolean function f if and only if Δf has no free face.
5.35Prove the following:
- If f and g are monotone increasing Boolean functions with the same variables, then
 .
. - If Δf or Δg is noncollapsible, then
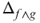 is noncollapsible.
is noncollapsible.
5.36 Compute the Euler characteristic of the simplicial complex whose maximal faces are the following:

Prove that this simplicial complex is noncollapsible. (This is an example that a connected noncollapsible simplicial complex has the Euler characteristic 1.)
5.37 Prove that if Δ is collapsed to Σ by a sequence of elementary collapses, then ![]() can be collapsed to
can be collapsed to ![]() by a sequence of elementary collapses.
by a sequence of elementary collapses.
5.38 Let ![]() be a Boolean function. Let
be a Boolean function. Let ![]() . Prove the following:
. Prove the following:
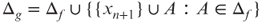 .
.- Δg is collapsible. (It is easy to prove it by the topological criterion. Can you also prove it by the definition of collapsibility?)
5.39 Prove that the linear extension of an automorphism has a fixed point on the geometric representation of the simplicial complex if and only if the automorphism has a nonempty fixed face in the simplicial complex.
5.40 Consider graphs G of order n for some even number n. Let ![]() be the property of G not being bipartite. Prove that every automorphism of
be the property of G not being bipartite. Prove that every automorphism of ![]() has a nonempty fixed face.
has a nonempty fixed face.
5.41 Let vertices of a simplicial complex be labeled by elements in ![]() and ϕ an automorphism defined by
and ϕ an automorphism defined by ![]() . Prove that if n is odd, then all edges can be decomposed into
. Prove that if n is odd, then all edges can be decomposed into ![]() orbits of cardinality n and if n is even, then all edges can be decomposed into
orbits of cardinality n and if n is even, then all edges can be decomposed into ![]() orbits of cardinality n and one orbit of cardinality
orbits of cardinality n and one orbit of cardinality ![]() . Moreover, the set of edges
. Moreover, the set of edges ![]() is a system of distinct representatives for the orbits.
is a system of distinct representatives for the orbits.
5.42 Prove that the property of graphs being bipartite is elusive.
5.43 Let ![]() be the set of graphs with n vertices whose maximum degree is at most k. Then
be the set of graphs with n vertices whose maximum degree is at most k. Then ![]() is elusive for
is elusive for ![]() .
.
5.44 Let ![]() be a nontrivial monotone property of graphs of order n. Apply the topological approach of Sections 1.6–1.8 to prove that
be a nontrivial monotone property of graphs of order n. Apply the topological approach of Sections 1.6–1.8 to prove that ![]() , where q is the largest prime power less than n.
, where q is the largest prime power less than n.
5.45 A one-dimensional complex is a simplicial complex such that all its nonempty faces are edges and vertices. Prove that a collapsible one-dimensional complex having a transitive group of automorphisms is either a single vertex or an edge.
5.46 Let Δ be a nonempty simplicial complex over X, where ![]() with
with ![]() , a prime power. Prove that if
, a prime power. Prove that if ![]() for every
for every ![]() and Δ is invariant under Γ, a transitive group of permutations on X1, then Δ is elusive. (Δ is elusive if the function f with
and Δ is invariant under Γ, a transitive group of permutations on X1, then Δ is elusive. (Δ is elusive if the function f with ![]() is elusive.)
is elusive.)
5.47 Prove that acyclic property of digraphs is elusive.
5.48 Suppose that H is a graph whose automorphism group is transitive on its vertices. Then each component of H is either factor-critical or contains a 1-factor. (A graph is called factor-critical if, after deleting a vertex, it has a 1-factor.)
5.49 Is every program of length r over a monoid M equivalent to a branching program of width ![]() and length r?
and length r?
5.50 Prove that ![]() (n ≥ 2) can be computed by a branching program of width 2 and cannot be computed by any permutation branching program of width 2.
(n ≥ 2) can be computed by a branching program of width 2 and cannot be computed by any permutation branching program of width 2.
5.51 Design a permutation branching program computing ![]() . Is your program the shortest?
. Is your program the shortest?
5.52 Let ![]() be three positive numbers. Consider a k-coloring of the set
be three positive numbers. Consider a k-coloring of the set ![]() . If
. If ![]() , then there exists a sequence
, then there exists a sequence
of integers such that all ![]() have the same color.
have the same color.
Historical Notes
The study of decision tree complexity was started with research on graph and digraph properties by Holt and Reingold (1972), Best et al. (1974), and Kirkpatrick (1974). Milner and Welsh (1976) discovered the simple strategy for the elusiveness of many graph properties. Aanderaa and Rosenberg (see Rosenberg (1973) and Best et al. (1974)) proposed the conjecture that for every nontrivial monotone graph property ![]() ,
, ![]() . This conjecture was confirmed by Rivest and Vuillemin (1975, 1976) (our Theorem 5.18). Meanwhile, they proposed a new one, that every nontrivial weakly symmetric function is elusive. Illies (1978) found a counterexample to the Rivest–Vuillemin conjecture. This counterexample suggests a modified conjecture: every nontrivial, weakly symmetric, monotone function is elusive. Gao, Hu, and Wu (1999) and Gao et al. (1999) showed that this modified conjecture is true for n = 6 and n = 10. The lower bound in Theorem 5.18 was improved subsequently to
. This conjecture was confirmed by Rivest and Vuillemin (1975, 1976) (our Theorem 5.18). Meanwhile, they proposed a new one, that every nontrivial weakly symmetric function is elusive. Illies (1978) found a counterexample to the Rivest–Vuillemin conjecture. This counterexample suggests a modified conjecture: every nontrivial, weakly symmetric, monotone function is elusive. Gao, Hu, and Wu (1999) and Gao et al. (1999) showed that this modified conjecture is true for n = 6 and n = 10. The lower bound in Theorem 5.18 was improved subsequently to ![]() by Kleitman and Kwiatkowski (1980) and to
by Kleitman and Kwiatkowski (1980) and to ![]() by Kahn et al. (1984). Karp conjectured that every nontrivial monotone graph property is elusive (see Kahn et al. (1984) and King (1989, 1990)). This conjecture was also proposed independently by other people (see Best et al. (1974) and Bollobas (1978)). The topological approach was first introduced by Kahn et al. (1984). They used this approach to prove Theorem 5.34. Theorem 5.31 is due to Yao (1986), and Theorem 5.35 is from Triesch (1994). The fixed point theorem on group actions on complexes (Theorem 5.32) came from Oliver (1975).
by Kahn et al. (1984). Karp conjectured that every nontrivial monotone graph property is elusive (see Kahn et al. (1984) and King (1989, 1990)). This conjecture was also proposed independently by other people (see Best et al. (1974) and Bollobas (1978)). The topological approach was first introduced by Kahn et al. (1984). They used this approach to prove Theorem 5.34. Theorem 5.31 is due to Yao (1986), and Theorem 5.35 is from Triesch (1994). The fixed point theorem on group actions on complexes (Theorem 5.32) came from Oliver (1975).
For random decision tree complexity, Yao (1977) conjectured that for any nontrivial monotone graph property ![]() ,
, ![]() for some constant c. Karp conjectured the bound can be improved to
for some constant c. Karp conjectured the bound can be improved to![]() . Yao (1987) and King (1989, 1990) made progress on this conjecture. Branching programs were first introduced by Lee (1959) as a model for switching functions. Borodin et al. (1983) studied branching programs of width 2. The work on permutation branching programs is due to Barrington (1990) and Barrington and Straubing (1991). Theorem 5.51 is from Cai and Lipton (1994).
. Yao (1987) and King (1989, 1990) made progress on this conjecture. Branching programs were first introduced by Lee (1959) as a model for switching functions. Borodin et al. (1983) studied branching programs of width 2. The work on permutation branching programs is due to Barrington (1990) and Barrington and Straubing (1991). Theorem 5.51 is from Cai and Lipton (1994).
