Chapter 8
Probabilistic Machines and Complexity Classes
Once you have mathematical certainty, there is nothing left to do or to understand.
—Fyodor Dostoevsky
We develop, in this chapter, the theory of randomized algorithms. A randomized algorithm uses a random number generator to determine some parameters of the algorithm. It is considered as an efficient algorithm if it computes the correct solutions in polynomial time with high probability, with respect to the probability distribution of the random number generator. We introduce the probabilistic Turing machine (PTM) as a model for randomized algorithms and study the relation between the class of languages solvable by polynomial-time randomized algorithms and the complexity classes P and NP.
8.1 Randomized Algorithms
A randomized algorithm is a deterministic algorithm with the extra ability of making random choices during the computation that are independent of the input values. Using randomization, some worst-case scenarios may be hidden so that it only occurs with a small probability, and so the expected runtime is better than the worst-case runtime. We illustrate this idea by examples.
Example 8.1
In the above, we have seen an example in which the randomized algorithm does not make mistakes and it has an expected runtime lower than the worst-case runtime. We achieved this by changing a deterministic parameter i into a randomized parameter that transforms a worst-case input into an average-case input. (Indeed, all inputs are average-case inputs after the transformation.) In the following, we show another example of the randomized algorithms that runs faster than the brute-force deterministic algorithm but might make mistakes with a small probability. In this example, we avoid the brute-force exhaustive computation by a random search for witnesses (for the answer NO). A technical lemma shows that such witnesses are abundant and so the random search algorithm works efficiently.
Example 8.2
The claim (1) is obvious because the algorithm outputs NO only when a witness 
is found such that 
. The claim (2) follows from the following lemma. Let 
.
Lemma 8.3
Proof
Our third example is the problem of testing whether a given integer is a prime number.
PRIMALITY TESTING (PRIME): Given a positive integer N in the binary form, determine whether N is a prime number.
PRIME is known to be in P, but all known deterministic algorithms are very slow. The following randomized algorithm gives a simple faster solution, with an arbitrarily small error probability ε. The algorithm searches for a witness that asserts that the given input number is a composite number. A technical lemma shows that if the given number is a composite number, then there are abundant witnesses and, hence, the error probability is small.The technical lemmas are purely number-theoretic results, and we omit the proofs.
Example 8.4
Lemma 8.5
Lemma 8.5 above shows that the Legendre–Jacobi symbols can be computed by a polynomial-time algorithm similar to the Euclidean algorithm for the greatest common divisors.
Now we are ready for the randomized algorithm for primality testing.
Randomized Algorithm for PRIMEInput: n, ε;let;for
to k dobegin
end;Output YES and halt.
- choose a random x in the range
;
- if
then output NO and halt;
- if
then output NO and halt;
From the polynomial-time computability of the Legendre–Jacobi symbols, the above algorithm always halts in polynomial time. In addition, by Euler's criterion, if n is a prime, then the above algorithm always outputs YES. Finally, the following lemma establishes the property that if n is a composite number, then the above algorithm outputs NO with probability 
.
Lemma 8.6
The above examples demonstrate the power of randomization in the design and analysis of algorithms. In the following sections, we present a formal computational model for randomized computation and discuss the related complexity problems.
8.2 Probabilistic Turing Machines
Our formal model for randomized computation is the PTM. A multi-tape probabilistic Turing machine (PTM) M consists of two components 
, where 
is a regular multi-tape DTM and ϕ is a random-bit generator. In additionto the input, output, and work tapes, the machine M has a special random-bit tape. The computation of the machine M on an input x can be informally described as follows: At each move, the generator ϕ first writes a random bit b = 0 or 1 on the square currently scanned by the tape head of the random-bit tape. Then the DTM 
makes the next move according to the current state and the current symbols scanned by the tape heads of all (but output) tapes, including the random-bit tape. The tape head of the random-bit tape always moves to the right after each move.
For the sake of simplicity, we only define formally the computation of a 2-tape PTM, where the first tape is the input/output/work tape and the second tape is the random-bit tape. Also, we will use a fixed random-bit generator ϕ that, when asked, outputs a bit 0 or 1 with equal probability. This generator, thus, defines a uniform probability distribution U over infinite sequences in 
.
With this fixed uniform random-bit generator ϕ, a 2-tape PTM M is formally defined by five components 
, which defines, as in Section 1.2, a 2-tape DTM 
, with the following extra conditions:
.- The function δ is defined from
to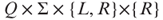 
. (That is, the random-bit tape is a read-only tape holding symbols in {0,1} and always moves to the right.)
From the above conditions, we define a configuration of M to be an element in 
. Informally, a configuration 
indicates that the machine is currently in the state q, the current tape symbols in the first tape are 
, its tape head is currently scanning the first symbol of t, the random-bit tape contains symbols α that were generated by ϕ so far, and its tape head is scanning the cell to the right of the last bit of α. (Note that the random-bit tape symbols α do not affect the future configurations. We include them in the configuration only for the convenience of the analysis of the machine M.) Recall that 
is the next-configuration function on the configurations of the machine 
. Let 
and 
be two configurations of M. We write 
and say that γ2 is a successor of γ1, if there exists a bit 
such that
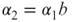, and
.
(Informally, b is the random bit generated by ϕ at this move. Thus the configuration 
of the DTM 
shows, in addition to the configuration of the PTM M, the new random bit b to be read by 
.) We let 
denote the reflexive transitive closure of 
.
For each input x, let the initial configuration be γx, that is, 
. We say that a configuration γ1 of M is a halting configuration if there does not exist a configuration γ2 such that 
. In the following, we write 
to mean that α is an initial segment of β.
Definition 8.7
The above definition involves the probability on the space of infinite sequences 
and is not convenient in the analysis of practical randomized algorithms. Note, however, that in each halting computation, the machine M only uses finitely many random bits. Therefore, there is an equivalent definition involved only with the probability on finite strings in 
. To be more precise, we treat 
as a 2-input DTM that satisfies the conditions (1) and (2) above. We assume that initially the first tape holds the first input 
, with all other squares having blank symbols B, and its tape head scans the first symbol of x. Also assume that the second tape initially contains the second input 
, with all other squares having a symbol 0,2 and the tape head scans the first symbol of α.
Proposition 8.8
Proof
For notational purposes, we write 
to denote that M accepts x and 
to denote that M rejects x. That is, M(x) is a random variable with the probability 
and 
.
Definition 8.9
Our definition above appears arbitrary when, for instance, 
. An alternative stronger definition for the set L(M) requires that if 
, then the rejecting probability of M(x) is greater than 1/2 and if both the accepting probability and the rejecting probability of M(x) are 
, then let M(x) be undefined. For time-bounded probabilistic computation, however, to be shown in Proposition 8.15, these two definitions are essentially equivalent.
Finally, we point out some discrepancies between our model of PTMs and practical randomized algorithms. The first difference is that we have simplified the model so that the random-bit generator ϕ can only generate a bit 0 or 1. In practice, one might wish to get a random number i in any given range. For instance, our model is too restrictive to generate a random number 
with 
. We might solve this problem by extending the model of PTMs to allow more general random number generators. Alternatively, we could just approximate the desired random number by our fixed random-bit generator ϕ (cf. Exercise 8.5).
The second difference is that in our formal model of PTMs, we defined the random-bit generator ϕ to generate a random bit at every step, no matter whether the deterministic machine 
needs it or not. In practice, we only randomize a few parameters when it is necessary. We could modify our definition of PTMs to reflect this property. Exercise 8.4 shows that these two models are equivalent. In many applications, we note, however, the model of Exercise 8.4 is more practical because the generation of a random bit could be much costlier than the runtime of the deterministic machine 
.
8.3 Time Complexity of Probabilistic Turing Machines
The time complexity of a PTM can be defined in two ways: the worst-case time complexity and the expected time complexity. The worst-case time complexity of a PTM M on an input x measures the time used by the longest computation paths of M(x). The expected time complexity of M on x is the average number of moves for M(x) to halt with respect to the uniform distribution of the random bits used. In both cases, if 
1, then the time complexity of M on x is ∞.
Definition 8.10
Definition 8.11
The expected time complexity is a natural complexity measure for randomized algorithms. People often use this complexity measure in the analysis of randomized algorithms. In the theory of polynomial-time computability, however, we will mostly work with the worst-case time complexity of PTMs. The main reason is that the worst-case time complexity is consistent with the time complexity measures of deterministic and nondeterministic machines, allowing us to study them in a unified model. In addition, for time- and error-bounded probabilistic computations, the worst-case time complexity is very close to the expected time complexity, as shown in the following proposition. We say two PTMs, M1 and M2, are equivalent if 
, and they are strongly equivalent if 
for all inputs x.
Proposition 8.12
Proof
As we are going to work mostly with the worst-case time complexity, we restrict ourselves to PTMs with a uniform time complexity. A PTM M has a uniform time complexity t(n) if for all x, for all α, 
, 
halts in exactly 
moves. The following proposition shows that we do not lose much by considering only PTMs with uniform time complexity.
Proposition 8.13
Proof
We are ready to define the complexity classes of probabilistic computation.
Definition 8.14
In Definition 8.9, the set L(M) was defined to be the set of all strings x with the accepting probability greater than 
and all other strings are defined to be in 
. A slightly stronger definition requires that for all 
, its rejecting probability is greater than 1/2. The following proposition shows that the class PP is robust with respect to these two different definitions.
Proposition 8.15
Proof
We defined the class PP as the class of sets accepted by some polynomial-time PTMs. Our goal is to define the class of sets feasibly computable by randomized algorithms. Does the class PP really consist of probabilistically feasible sets? The answer is NO; the class PP appears too general, as demonstrated by the following relations.